多维非平稳随机激励下隔震曲线梁桥的非线性振动控制

李喜梅， 王建成， 母渤海

(1. 兰州理工大学 西部土木工程防灾减灾教育部工程研究中心，兰州 730050；2. 兰州理工大学 防震减灾研究所，兰州 730050； 3. 中国市政工程西北设计研究院有限公司，兰州 730050)

地震波通过地面传播时，地面运动是复杂的多维运动，除了我们一般所熟知的3个平动分量外，还有3个转动分量(一个绕竖轴旋转的扭转分量和两个绕水平轴旋转的摇摆分量)。在一般结构(质量中心和刚度中心相重合且在一条直线上的结构)的抗震分析中，分别沿着两个主轴方向进行计算是可靠的，但对于质量中心和刚度中心不重合的结构，地震作用在质量中心的惯性力将对刚度中心产生扭转，迫使结构产生扭转耦联振动。所以，对于不规则结构，应该考虑地震动的扭转分量。事实上，无论是对于规则还是不规则结构，在多维地震作用下的响应都要大于单维地震，尤其是对于不规则结构[1-2]。另外，由于实际的地震动是一个非平稳随机过程，因此对结构进行非平稳随机振动分析更符合实际地震动过程。

在公路及城市道路的立体交叉体系中，由于受周围环境、交通线路等因素的限制，需要采用曲线桥实现各方向的交通互联，保证交通线路顺畅，改善城市交通的紧张状况[3]。在强烈的地震作用下，桥梁一般会发生弹塑性变形，使得桥梁抗震成为突出问题。尽可能地降低公路桥梁的地震响应一直是学者们研究的重点[4-5]。目前，针对直线连续梁桥减震控制方法已做了大量研究[6-7]。曲线桥梁的减隔震控制在国内也已开始理论上[8-9]的探索，但由于曲线桥结构形式复杂，现有的研究还远不能满足实际工程的需要[10]。因此，对隔震曲线梁桥控制问题的研究具有重要意义。亓兴军等[11-14]建立了曲线梁桥的有限元模型，用不同的减隔震方法对曲线梁桥的振动控制进行了深入的研究，但以上研究未考虑地震激励的随机性，且有限元建模分析较复杂，工作量大，计算效率低。为了简化分析，提高计算效率，王丽等[15-16]根据曲线梁桥的受力特点，建立了适合分析隔震曲线梁桥的简化模型，并验证了简化模型的正确性及精度。李喜梅等[17]利用双质点六自由度线性简化模型，采用序列最优控制(sequential optimal control，SOC)算法对一座三跨隔震曲线梁桥进行了非平稳随机激励下的振动控制分析，但未考虑强震作用下曲线梁桥进入非线性的情况。

本文在已有的双质点六自由度简化模型的基础上，采用经典的Bouc-Wen模型，建立考虑上部结构偏心的隔震曲线梁桥的弹塑性模型，输入考虑扭转分量的多维非平稳随机激励(仅考虑强度非平稳)，研究隔震曲线梁桥随机动力响应，并采用序列最优控制算法和经典最优控制(classical optimal control，COC)算法对结构的动力响应进行振动控制分析。

1 隔震曲线梁桥振动方程的建立

1.1 模型假设

本文采用李喜梅等提出的隔震曲线梁桥的简化模型，分析隔震曲线梁桥的非线性动力响应，具体的简化剪切模型如下：

分别将隔震曲线梁桥桥墩及上部结构简化为两个各具两水平x，y自由度与一个围绕质量中心轴扭转θ自由度的堆积质量m1，m2模型系统，桥墩与上部结构为两质点非同轴质量偏心结构的分析模型，上下质点分别表示曲线桥上部、下部结构。简化模型如图1所示。

图1 隔震曲线梁桥简化模型Fig.1 Simplified model of isolated curved beam bridge

1.2 非线性运动方程的建立

取隔震曲线梁桥为剪切型，将隔震曲线梁桥的上部结构和下部结构分别记为层。以隔震曲线梁桥上部结构的质量中心为坐标原点，建立隔震曲线梁桥的非线性振动控制方程，表示如下

(1)

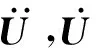
(2)

(3)

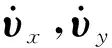
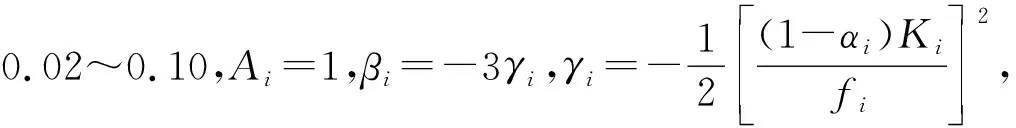
由此，可以写出隔震曲线梁桥的等效线性化方程

(4)

(5)

式中，Ceq，Keq为Bouc-Wen模型的等效阻尼矩阵和等效刚度刚度，Bouc-Wen模型的具体的等效线性化过程详见文献[20]。

式(4)与式(5)中各矩阵的具体形式如下所示。

质量矩阵

式中：m1，m2分别为隔震曲线梁桥的下、上部结构质量；J1，J2分别为下、上部结构转动惯量[21]；ri为结构的回转半径；Xmi，Ymi分别为桥梁下、上部结构质心相对于参考轴的坐标。

弹性刚度矩阵

式中，Kxx，Kyy分别为结构在x，y向弹性平动刚度，取隔震曲线桥梁结构为剪切型，故

式中：kxri，kyri为第i层第r个桥墩位置处x，y向的抗侧刚度；l为曲线梁桥桥墩(或支座)的数目；Kxi为第i层x向的屈服前的水平总刚度；αi为第i层屈服后和屈服前的水平刚度之比，当αi=0时，表示结构的第i层处于完全非线性状态，当αi=1时，表示结构的第i层处于弹性状态；Kyy与Kxx在形式上完全相同，只是将矩阵中的Kxi换成Kyi。

Kxθ，Kyθ，Kθθ分别为隔震曲线梁桥在x，y向的弹性平扭刚度和扭转刚度，其中

其中，Kxθij为第i层不动，仅j层发生x向单位位移时，在第i层所需施加的力矩；同样，Kyθ与Kxθ在形式上完全一致，各元素Kyθij为第i层不动，仅j层发生y向单位位移时，在第i层所需施加的力矩；Kθθij为第i层不动，仅j层发生单位转角时，在第i层所需施加的力矩[22]。

塑性刚度矩阵

Kxh，Kyh分别为结构在x，y向塑性平动刚度，Kθxh，Kθyh分别为x，y向塑性平扭刚度。其中

Kyh，Kθxh，Kθyh与Kxh在形式上是完全一致的，只不过是将矩阵中的Kxi分别换为Kyi，-Kxieyi，Kyiexi。这里，exi，eyi分别为第i层质心与刚心沿y，x方向的距离，表示为：exi=xri-xmi，eyi=yri-ymi。xri，yri为第i层第r个桥墩沿x，y向坐标；xmi，ymi为第i层质心的x，y向坐标。

阻尼矩阵C用分区瑞利阻尼

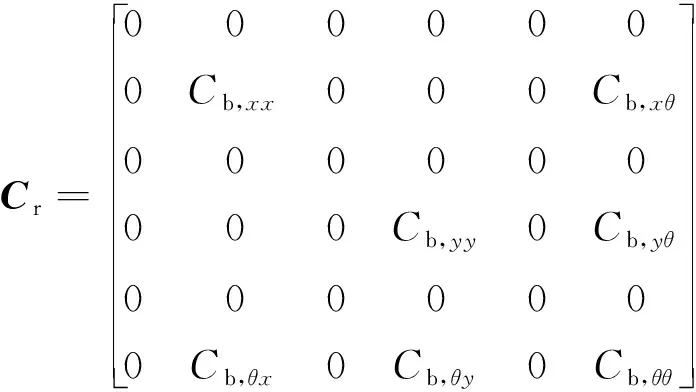
式中：C0为经典瑞利阻尼矩阵；Cr为非比例阻尼的余项阻尼矩阵，Cr中的各元素的计算可参考文献[23]。αs，βs为下部结构瑞利阻尼的比例系数，即

式中：ξs为下部结构的阻尼比；ωi，ωj为结构第i，j阶圆频率。

地震作用影响矩阵E=[Ix,Iy,Iθ]，其中，Ix=[12×1,02×1,02×1]T，Iy=[02×1,12×1,02×1]T，Iθ=[02×1,02×1,12×1]T。

等效阻尼矩阵和等效刚度矩阵具体形式如下所示

将式(4)与式(5)转化为状态空间表达式如下所示

(6)

(7)

式中，I为单位矩阵。选择输出各质点相对于地面的位移、加速度以及层间滞回位移，则输出矩阵为

2 序列最优算法

2.1 运动方程的等效线性化

引用滞变位移项为零的假定，建立Bouc-Wen模型的等效线性化表达式[24]。该方法首先由Yang等[25]提出，并用于瞬时最优控制。杜永峰等[26]将该方法用于序列最优控制，对滞变智能隔震结构进行了振动控制研究。本文也采用零滞变位移这一等效线性化方法，对隔震曲线梁桥进行振动控制，则状态方程变为

(8)

(9)

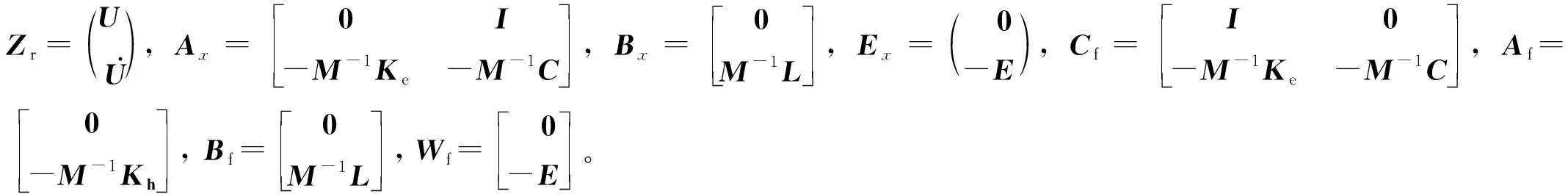
2.2 基于状态反馈的最优控制力模型

本文对进入弹塑性的隔震曲线梁桥进行振动控制分析时，建立控制力和状态向量的关系是借用线性最优控制的理论，故将目标函数改为等效线性化后的状态变量。

(10)

式中：Q，R分别为结构动力响应和控制力的权重矩阵；t0，tf分别为控制的开始时刻和结束时刻。

按照杜永峰等的推导方法可以得出序列最优控制力模型如下所示

(11)

(12)

(13)

式中，λ为Lagrange乘子向量，基于式(8)、式(9)的状态方程，仿照杜永峰等的推导思路，可以推出最优控制力表达式为

(14)

式中： Δt为时间间隔；tA为当前时刻；IrH(m)，ErH(m)为最优控制力系数；m对应终止时刻的时间步长数；各矩阵的具体表达式见杜永峰等的研究。

将式(14)代入式(6)中得

(15)

式中：ARc(m)=AR+ΔtBRIrH(m)；ERc(m)=ER+(Δt)2BRErH(m)。

由于在状态转移算法中Δt通常取值很小，则ERc(m)可近似取为

ERc(m)=ER

(16)

由于ARc(m)是随时间变化的，这种情况不便于进行频域内的响应分析。为了简化分析，本文将ARc(m)表达式中的时变部分进行加权平均，将其变为时不变表达式。首先计算闭环反馈增益矩阵的加权平均值

(17)

式中：Td为地震动持时；Te为控制延时。由此可以得到时不变的控制等效动力特性矩阵

ARc=AR+BRKRf

(18)

由以上推导，最终可以得到我们所要的状态空间方程

(19)

3 隔震曲线梁桥随机地震响应的求解

(20)

(21)

将式(21)利用欧拉公式变形得

(22)

对于一阶微分方程式(19)，本文将虚拟激励变为简谐外荷载后，采用文献[29]中提出的混合精细积分法进行计算，得到隔震曲线梁桥的随机动力响应，从而求出结构的功率谱矩阵为

SVV(ω,t)=V(ω,t)*·V(ω,t)T

(23)

式中： *为共轭； T为转置。

结构的时变方差为

(24)

4 算例与讨论

4.1 工程背景

某立交匝道上一联圆曲线连续梁桥，该桥共有3跨，每跨20 m，曲率半径R=50 m，圆心角α=69°。主梁采用单箱单室箱梁，桥面宽度8 m，圆柱形桥墩，直径1.6 m，墩高7 m，下部结构的阻尼比ξs=0.05，每个墩顶分别布置一个直径为500 mm的铅芯橡胶支座，隔震层的水平阻尼比ξb=0.15。

取曲线桥上部结构质量中心为整体坐标系原点，其平面布置图如图2所示。每个桥墩处径向、切向的阻尼器布置图如图3所示。曲线梁桥相应模型计算参数如表1所示。

图2 曲线桥平面布置图(m)Fig.2 Plan view of curved bridge (m)

图3 径向、切向阻尼器布置图Fig.3 Radial and tangential dampers layout

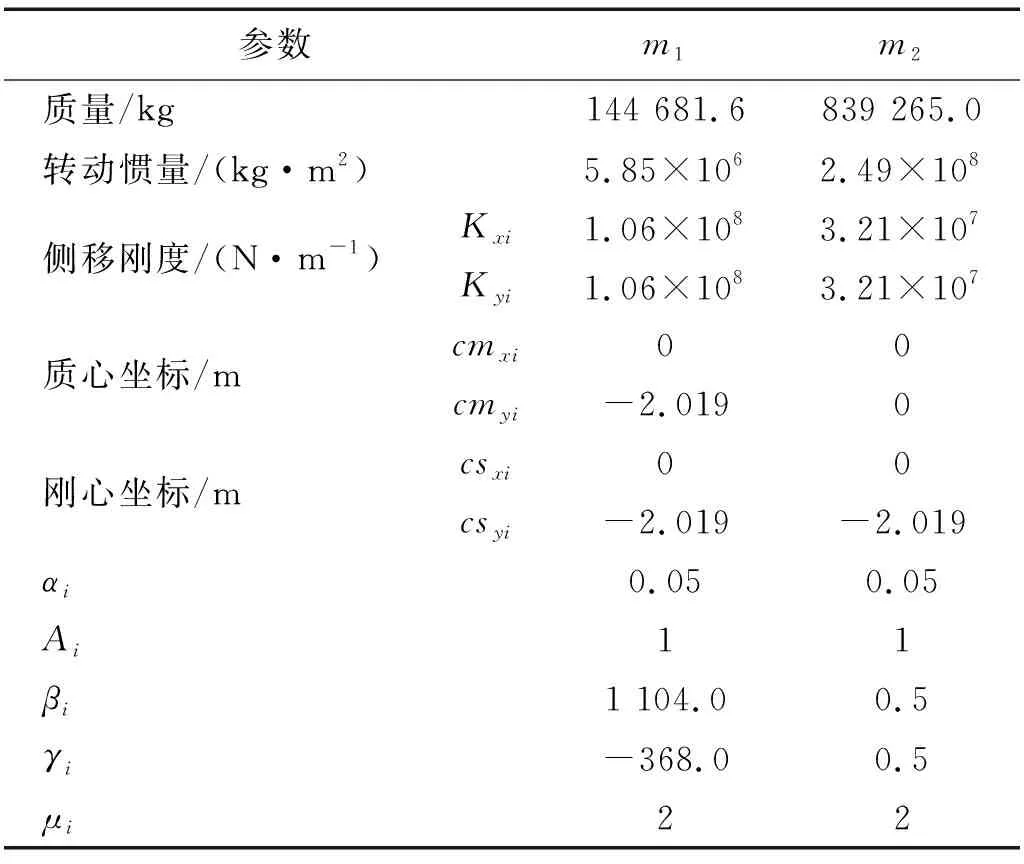
表1 曲线桥相应模型的计算参数Tab.1 Calculation parameters of corresponding model of curved bridge

4.2 多维地震动的随机模型

带有低频过滤器的双过滤白噪声地震功率谱更适用于隔震结构的随机响应分析[30]。综合考虑几种常见的地震动加速度功率谱的优缺点，本文选取Clough-Penzien模型作为随机振动分析中水平分量的功率谱模型，其自谱密度函数为

(25)

式中：ωg和ξg分别为场地土的卓越圆频率与阻尼比；S0为基岩加速度(白噪声)自谱密度；ξf和ωf两参数的配合可模拟地震动低频能量的变化，通常取ξf=ξg，ωf=0.1-0.2ωg[31]。

本文以地震动烈度为8度为例，推算出罕遇地震0.4g下的单边功率谱强S0=2.177 4×10-2m2/s3，场地选用Ⅱ类场地，设计地震分组为第二组，则式(25)的地震动随机模型参数取为[32]：ωg=15.71，ωf=0.15ωg，ξf=ξg=0.72，其输入的功率谱密度曲线如图4所示，地震动持时取T=20 s。

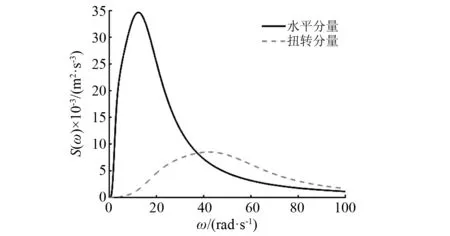
图4 加速度功率谱密度函数Fig.4 Acceleration power spectral density function

扭转分量地震动随机模型选用李宏男[33]提出的转动功率谱数学模型

(26)

式中：γ为低频减量系数；ωg1和ξg1为土层过滤器的频率和阻尼比；ωg2和ξg2可为基岩过滤器的频率和阻尼比；S0为基岩谱强度。式(26)中模型的参数取值见李宏男的研究，其输入的功率谱密度曲线如图4。

非平稳随机地震动模型的调制函数g(t)选用工程中常用的三段式均匀调制函数，其表达式如下

(27)

式中：c为衰减系数；t1和t2分别为主振平稳段的首、末时间。式(27)中参数取值为：c=0.35，t1=0.8 s，t2=7.0 s。

4.3 结构随机响应分析

为了研究考虑扭转分量的多维非平稳随机激励对隔震曲线梁桥动力响应的影响，本文输入多维非平稳随机激励，假定水平分量随机激励的输入角度θ=0°(与整体坐标系x轴方向的夹角)，分别求出考虑与未考虑扭转分量下上部结构x，y向的位移功率谱密度和时变方差的变化规律。结果如图5、图6所示。

为了能清楚的描述其变化规律，对上部结构位移功率谱密度各分图横坐标取对数进行绘制。由图5可知，在考虑扭转分量与未考虑扭转分量的非平稳随机激励下，上部结构x向的位移功率谱密度的峰值位置是一致的，均位于隔震曲线梁桥一阶自振频率附近。隔震曲线梁桥上部结构x向位移功率谱密度峰值与未考虑扭转分量的相比，由原先的3.63 cm2/s增加至3.72 cm2/s，增加了2.5%。由图6可知，隔震曲线梁桥在罕遇非平稳随机激励下，位移响应呈现强烈的非平稳性，时滞现象较明显。当考虑非平稳随机激励的扭转分量后，隔震曲线梁桥上部结构x向峰值位移方差与未考虑扭转分量的相比，由原先的64 cm2增加至67 cm2，增加了4.5%。由于本文中的隔震曲线梁桥仅在y方向上存在偏心，故非平稳随机激励的扭转分量对隔震曲线梁桥上部结构y向的位移功率谱密度和时变方差无影响。由以上分析可以看出，考虑扭转分量的多维非平稳随机激励下隔震曲线梁桥的动力响应要大于仅考虑水平双向非平稳随机激励下的响应，因此，有必要对考虑扭转分量的非平稳随机激励下的隔震曲线梁桥其进行振动控制。

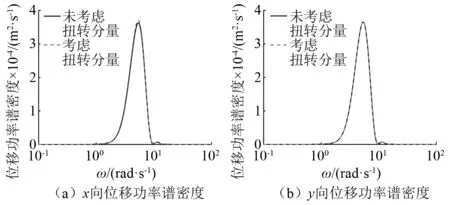
图5 上部结构位移功率谱密度曲线Fig.5 Displacement power spectral density curve of superstructure

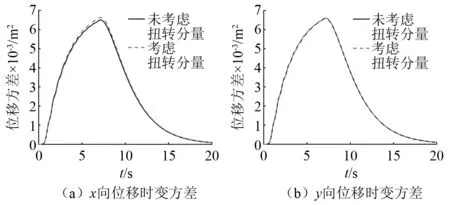
图6 上部结构位移时变方差曲线Fig.6 Displacement time-varying variance curve of superstructure

4.4 振动控制分析

本文采用状态反馈的序列最优控制和经典线性最优控制对考虑扭转分量的多维非平稳随机激励下的隔震曲线桥进行振动控制，假设控制器能够实时提供结构所需要的控制力。控制效果以上部结构的动力响应为评价指标。输入多维非平稳随机激励，分别求出隔震曲线梁桥上部结构在无控、经典最优控制和序列最优控制下的功率谱密度和时变方差变化规律。结果如图7～图10所示。

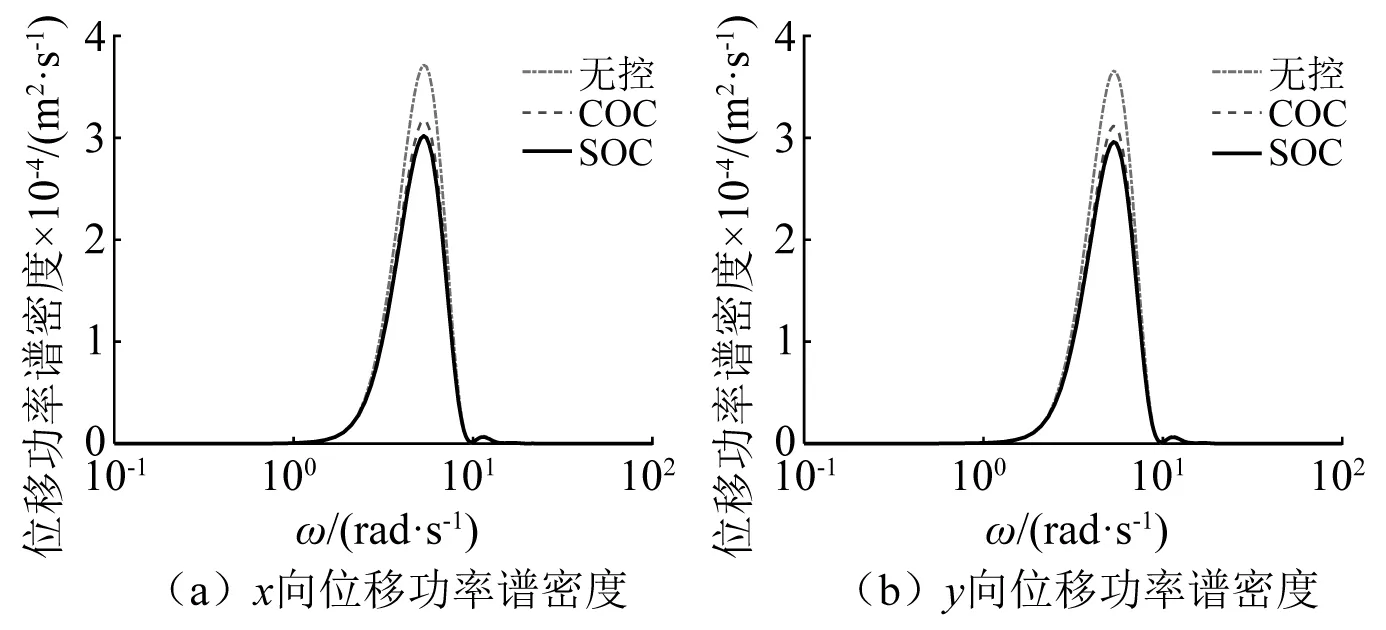
图7 上部结构位移功率谱密度Fig.7 Displacement power spectral density of superstructure

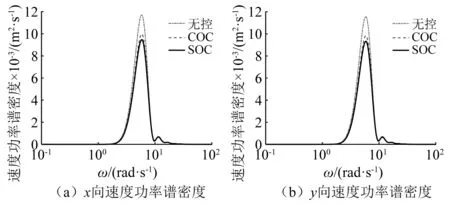
图8 上部结构速度功率谱密度Fig.8 Velocity power spectral density of superstructure

图9 上部结构位移时变方差Fig.9 Displacement time-varying variance curve of superstructure

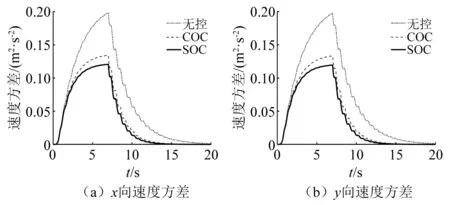
图10 上部结构速度时变方差Fig.10 Velocity time-varying variance curve of superstructure

图7和图8分别为隔震曲线梁桥在3种不同控制状态下，输入多维非平稳随机激励后的上部结构x，y向的位移功率谱密度和速度功率谱密度对比图。从图7和图8可知，在3种不同的控制状态下，隔震曲线梁桥的位移功率谱密度和速度功率谱密度的最大值都在结构一阶频率附近达到，且在经典最优控制和序列最优控制下，隔震曲线梁桥上部结构不管是x方向还是y方向的位移功率谱密度和速度功率谱密度都有了明显减小，隔震曲线梁桥的振动得到了有效地抑制。

在经典最优控制下，上部结构x向和y向的位移功率谱密度峰值与无控下相比，分别减少了42.4%和43.3%，速度功率谱密度峰值分别减少了44.6%和45.2%；在序列最优控制下，上部结构x向和y向的位移功率谱密度峰值与无控下相比，分别减少了51.5%和53.3%，速度功率谱密度峰值分别减少了52.5%和53.3%。

图9和图10分别为隔震曲线梁桥在3种不同控制状态下，输入多维非平稳随机激励后的上部结构x，y向的位移时变方差和速度时变方差对比图。从图9和图10可知，经典最优控制和序列最优控制在相同的能量下，隔震曲线梁桥上部结构不管是x方向还是y方向的位移时变方差和速度时变方差都有了明显减小，隔震曲线梁桥的振动得到了有效地抑制。运用经典最优控制算法控制后的上部结构x向和y向的位移方差峰值与无控下相比，分别减少了33.3%和34.8%，速度方差峰值分别减少了31.9%和32.6%；运用序列最优控制算法控制后的上部结构x向和y向的位移方差峰值与无控下相比，分别减少了40%和40.9%，速度方差峰值分别减少了38.1%和38.6%。另外，在经典最优控制和序列最优控制作用下，隔震曲线梁桥的时滞和非平稳现象得到很好的抑制。

5 结 论

本文运用经典的Bouc-Wen模型建立隔震曲线梁桥的非线性动力方程，将非线性方程等效线性化，输入考虑扭转分量的多维非平稳随机激励，利用欧拉公式将虚拟激励变为简谐外荷载，采用混合精细积分法分析隔震曲线梁桥的随机动力响应。基于零滞变位移条件的等效线性化方法求出序列最优控制的最优控制力，对隔震曲线梁桥的动力响应进行了控制分析，并与经典最优控制下的作对比，结论如下：

(1) 考虑扭转分量的多维非平稳随机激励下隔震曲线梁桥的动力响应要大于仅考虑水平双向非平稳随机激励下的响应，且在罕遇非平稳随机激励下，隔震曲线梁桥的位移响应呈现强烈的非平稳性，时滞现象较明显。

(2) 运用序列最优控制算法控制后的隔震曲线梁桥上部结构x、y向位移和速度功率谱密度和方差响应均得到了明显的减小，且对响应呈现出的非平稳性和时滞现象有明显的抑制效果，其控制效果与经典最优控制下的相当。