配网线路无人机自主巡检的路径规划方法

成 亮，杨 沛，贾燕翀，张磊源

(国网永济供电公司，山西 永济 044500)

0 引言

配电网作为电力系统的重要组成部分，承担着从输电网或地区发电厂接受电能，再通过配电设施就地分配或按电压逐级分配给各类用户的任务。配电网直接与供电用户相联系，因此，配电线路的安全稳定运行对整体电力供应系统的安全性起着至关重要的作用，更是社会稳定和百姓日常生活的基础[1]。配网线路分布具有点多面广的特点，很多线路位于地形复杂的野外，导地线、绝缘子塔杆以及其他金具容易受到雷电、风雪以及违章施工等自然和人为因素的破坏，因此，运维人员需要定期对配网线路进行巡检，以确保线路的正常运行[2-3]。传统的配网巡检方式是人工在地面以仰视角度靠肉眼进行观察，一方面，无法直接观察到线路设备高处或顶部的情况；另一方面，巡检安全性差且效率低下[4]。

近年来，随着无人机技术的飞速发展，无人机由于灵活、轻便、能到达人员无法到达或不便到达的地方等特点，在电力、交通、物流和农业植保等多个领域得到了广泛应用[5]。尤其在电力巡检领域，无人机作为新型巡检平台已广泛地应用于电力巡检业务的活动中。通过无人机可以实现对配网线路的精细化巡检，线夹断裂、螺栓松动、防振锤跑位和间隔棒松脱等人工巡检中不易发现的缺陷在无人机的高清影像中一目了然[6]。

无人机可以更加高效、安全地完成配网巡检任务，把巡检人员从高强度、高风险、重复性的体力劳动中解放出来[7-8]。目前，在使用无人机进行配电网巡检时，主要依靠巡检人员手动控制无人机拍摄杆塔和线路的图像[9]。在手动巡检模式下，巡检人员需要根据经验和技术，操控无人机飞到合适的位置，并调整云台以合适的角度对配网线路和杆塔进行拍照，这对巡检人员提出了较高的要求[10]。为了更好地发挥无人机的效能，需要研究无人机配网自主巡检技术。

配网巡检的主要工作包括对线路本体和杆塔关键部件的巡检，其中以拍摄杆塔上的绝缘子、避雷器和隔离刀闸等关键部件为主[11]。配网的杆塔数量较多、种类各异且分布较广，而无人机由于受到续航能力的约束，单架次飞行只能对部分杆塔进行巡检。与此同时，所有的杆塔都需要定期巡检，以保证关键部件的正常运行。如何在单次飞行中最大限度地发挥无人机续航能力，巡检尽可能多的杆塔，同时使得大部分杆塔2次巡检之间的间隔时间大致相同，是无人机配网自主巡检需要解决的主要问题。

本文主要研究了无人机对配网杆塔上的关键部件进行巡检的路径规划问题。首先，将配网杆塔抽象为点目标，并将每个杆塔距离上一次被巡检的间隔天数作为该点目标的权重；其次，使用定向问题(Orienteering Problem，OP)对问题进行建模，并通过引入模拟退火(Simulated Annealing,SA)算法的Metropolis策略提升了遗传算法(Genetic Algorithm,GA)的局部搜索能力；再次，基于OP的标准实例验证了本文模型和算法的正确性；最后，为了说明本文方法如何应用于真实场景，使用脱敏的配网线路真实数据进行了案例研究，说明本文所提出的算法能在合理的时间内得到无人机配网自主巡检的最优路径。

1 问题描述

下面将介绍配网线路无人机自主巡检路径规划问题的建模过程。

1.1 无人机

无人机从起点0出发，选择部分杆塔进行巡检，并在完成巡检任务后返回终点N+1，无人机从起飞到降落的总时长不能超过无人机的最大续航时长Tmax。假设无人机搭载了自动避障和增稳装置，具有自动避障和一定的抗风能力，因风力影响或避障产生的路径偏离相对于总飞行路径长度忽略不计。

1.2 待巡检的杆塔

用0和N+1分别表示无人机的起点和终点，集合T={1,2,…,i,…,N}为所有待巡检杆塔的集合，无人机的起点、终点以及所有待巡检杆塔组成的集合为A={0,1,…,i,…,N,N+1}。待巡检杆塔i的权重用wi(i∈T)表示，该权重表示杆塔i距离上一次被巡检的时间间隔，权重越大表示时间间隔越长，则杆塔被巡检的优先级也越高，需要尽快安排无人机对其进行巡检。

1.3 无人机的巡检任务执行时间

用P={0,i,…,j,N+1},i,j∈T表示无人机的巡检路径，无人机必须从起点出发执行巡检任务，并在执行完任务后最终回到终点。无人机在杆塔i与杆塔j之间的飞行时间tij为：

(1)

式中，dij为杆塔i与杆塔j之间的欧氏距离；v为无人机的飞行速度；A为所有顶点集合。

无人机巡检任务路径P对应的任务执行时间为：

(2)

1.4 数学模型

针对无人机配网自主巡检路径优化问题，以无人机所巡检杆塔的权重之和最大化作为优化问题的目标函数，建立如下数学模型：

(3)

约束条件为：

(4)

(5)

(6)

tP≤Tmax,

(7)

2≤ui≤N;∀i∈T,

(8)

ui-uj+1≤(N-1)(1-xij);∀i,j∈T,

(9)

xij∈{0,1};∀i,j∈T。

(10)

式(3)的目标函数表示无人机所巡检杆塔的权重之和最大化；式(4)表示无人机必须从起点出发，并最终返回终点；式(5)表示每个杆塔最多只能被巡检一次；式(6)是流量守恒约束，即每个节点的入度与出度相等；式(7)是无人机续航能力约束；式(8)和式(9)避免了子路径，其中ui为杆塔i在路径P中的排序；式(10)为二元决策变量的取值，当无人机巡检完杆塔i后飞往杆塔j巡检，则xij=1，否则，xij=0。

2 改进的遗传算法

2.1 遗传算法

GA是美国密歇根大学Holland教授[12]提出的一种启发式算法，模拟了自然界进化机制和生物进化论，是一类典型的群类算法[13]。由于GA是从一个群体开始搜索最优解，所以具有很强的并行搜索能力，同时，GA是一种与问题无关的算法，对参数的编码进行选择、交叉和变异等操作，不需要了解问题的相关知识，仅凭适应度函数对种群中的染色体进行评估。上述优点使得GA被广泛地应用于无人机路径规划等组合优化领域[14-16]。

经典GA包括以下4个步骤：

① 种群初始化。GA从构建一个初始种群开始，初始种群中包含若干条染色体，每条染色体都是一个按特定规则编码的问题可行解。

② 选择操作。即从父代种群中挑选出优秀的染色体进行后续遗传操作，使得种群中的优良基因得到传承。常见的选择算子有轮盘赌、随机抽样和锦标赛等。

③ 交叉操作。这一步是GA的核心，也是子代种群在父代种群基础上进行改良的最重要手段，常用的交叉方式有单点交叉和多点交叉等。

④ 变异操作。是为了避免出现早熟现象而对种群进行的扰动，即以一定的概率对种群中的部分染色体进行局部改变，以生成新的染色体，它模拟了生物遗传中的基因突变现象。

⑤ 适应度评估。GA的收敛速度和寻优能力主要取决于适应度函数的选取，其构建方法主要有2种：以目标函数作为适应度函数；基于目标函数的限界构造法，适应度评估涉及种群中的每一条染色体。

⑥ 种群更新。将父代种群中的优秀染色体和新生成的子代种群中的精英合并得到新的种群，体现了生物的遗传特征。

GA的优点是简单、快速、有效，尤其在算法的初期，寻优能力很强，但到了后期，由于种群中染色体的差异越来越小，使得进化速度越来越慢，而且容易陷入局部最优解[17]。虽然变异算子可能跳出局部最优，但总体效率偏低，若想改进算法的总体性能就需要提升算法的局部搜索能力。将群类算法与局部搜索算法混合是近年来比较流行的方法[18-20]，本文将SA算法与GA进行结合，设计了一种改进的遗传算法(Improved Genetic Algorithm，IGA)。

2.2 IGA

SA算法是一种模仿金属等固体物质退火过程的启发式算法[21-22]，当初始温度足够高、冷却过程足够长时，金属粒子都能达到基准稳态，从而使金属的强度大大加强。SA算法最重要的特征是概率跳跃特性，也被称为Metropolis过程，SA算法已被证明通过精确控制降温过程可以近似1的概率收敛到全局最优[23-24]，但由于条件比较苛刻且收敛速度太慢而无法满足实际应用的需求。

本文将SA算法的Metropolis准则引入到变异操作中，以提升GA的局部搜索能力。算法的伪代码如下：

改进的遗传算法(IGA)开始 初始化HGSA的相关参数种群初始化(详见2.2.1节)染色体的约束校验与调整(详见2.2.2节)种群的适应度评价(详见2.2.3节)while终止条件不满足交叉操作(详见2.2.4节)染色体的约束校验与调整引入Metropolis准则的变异操作(详见2.2.5节)种群的适应度评价种群更新操作(详见2.2.6节) endwhile 输出最优解结束

2.2.1 种群初始化

本文专门设计了一种整数编码染色体，由所有待巡检杆塔的编号组成，如图1所示。

图1 IGA染色体编码示意Fig.1 Schematic diagram of IGA chromosome coding

图1中的染色体表示无人机从站点出发后，依次巡检1号、7号、4号、3号和5号杆塔，然后返回站点。

按以下3个步骤完成种群初始化：

① 令T为无人机待巡检杆塔的集合，以无人机的起点为圆心，以无人机的续航能力Tmax为直径，构造“Tmax圆”，删掉集合T中在“Tmax圆”以外的点所对应的杆塔编号，得到无人机续航能力足以覆盖的杆塔集合T’；

② 将集合T’中的杆塔编号进行随机排列得到一条染色体，即无人机巡检杆塔的序列，也就是无人机的巡检路径P；

③ 根据预设的种群规模重复步骤①～步骤②，得到初始种群。

由于无人机的续航能力有限，所以初始种群中的染色体不一定是可行解，需要对种群中的每条染色体进行约束检验，并对不满足约束条件的染色体进行调整。

2.2.2 染色体的约束校验与调整

初始化以及交叉操作后的染色体有可能违反本文模型中的2个约束，即式(5)所代表的目标访问次数约束以及式(7)所代表的无人机续航能力约束。本文按如下步骤进行约束校验和调整：

① 判断染色体中是否存在相同的杆塔编号，如有则删除多余的编号，保证每个杆塔编号在每条染色体中只出现一次；

② 根据染色体编码计算无人机的路径长度，再除以无人机的飞行速度得到该路径对应的飞行时长，如果超过了无人机的续航时长，则按照杆塔的权重从小到大依次删除其编号，如果2个杆塔的权重相同，则优先删除距离更远的杆塔，直到该路径的飞行时长小于等于无人机的续航时长。

经过约束校验与调整后的染色体是问题的一个可行解。

2.2.3 种群的适应度评价

染色体的适应度代表了路径规划方案的优劣，适应度越大说明路径规划方案越好。因此，以式(3)作为算法的适应度函数，路径规划方案的收益越高，说明该方案越优。后续的交叉操作基于种群适应度评价的结果进行。

2.2.4 交叉操作

本文使用经典的轮盘赌方法从父代种群中选择染色体进行交叉操作，染色体的适应度越高，其优良的基因被遗传到下一代的可能性也越高。本文采用两点交叉方式，具体操作步骤如下：

① 使用经典的轮盘赌方法选择2条待交叉的染色体，记作父代A和父代B，生成一个[0,1]区间的随机数r，若r小于交叉概率PC则转步骤②，否则结束当前操作；

② 由于父代A和父代B的染色体长度可能不同，所以需要分别产生2个交叉位，然后将2个交叉位之间的基因片段进行互换，得到2条新的染色体子代C和子代D，双点交叉操作的过程如图2所示。

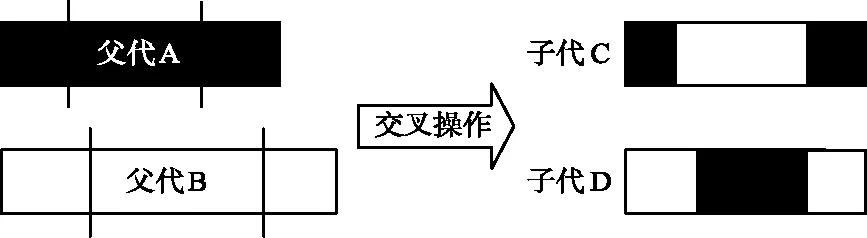
图2 双点交叉操作示意Fig.2 Schematic diagram of two-point crossover operation

2.2.5 引入Metropolis准则的变异操作

由于杆塔的权重不同，所以通过替换染色体中的杆塔编号有可能提升适应度。同时，对染色体进行路径长度校验，即改变对杆塔的巡检顺序有可能缩短无人机的路径长度，从而使得无人机可以访问更多的杆塔，提升染色体的适应度，所以本文设计了2种变异算子。

变异算子1：基因替换。随机选择1个基因位，使用无人机续航能力足以覆盖的杆塔集合T’中未出现在染色体中的杆塔编号替换该基因位上的杆塔编号。

变异算子2：基因调整。随机选择2个基因位，将这2个基因位上的杆塔编号进行互换。

在每次变异操作中，首先，随机选取1种变异算子生成1个新染色体；然后，使用2.2.2中的方法对新染色体进行约束校验和调整，并得到满足所有约束条件的新染色体；最后，运用Metropolis准则以一定的概率接收新染色体。

2.2.6 种群更新操作

种群更新操作是将新生的子代种群与父代种群进行合并的操作，具体步骤如下：

① 根据适应度值分别对子代种群与父代种群中的染色体进行排序；

② 根据公式N1=NP×Gap计算得到从子代种群中取出染色体的数量，其中NP是种群规模，Gap是代沟；

③ 根据公式N2=NP×(1-Gap)计算得到从父代种群中取出染色体的数量；

④ 从子代种群中取出适应度排名后N1位的染色体，与父代种群中适应度排名前N2位的染色体合并，得到一个新的种群，作为下一轮迭代的新种群。

3 实验与分析

本节所有实验均在i5-6500 CPU 3.2 GHz、内存8 GB的台式计算机上、Matlab R2020a的环境下运行。为了展示IGA的性能，本文设计了3组实验。第1组实验采用正交设计法对IGA的相关参数进行调优，以确定最优的参数组合；第2组实验基于OP标准实例数据集使用IGA进行求解，并与文献[25]中的最优解进行对比；第3组实验使用脱敏的配网线路真实数据，使用IGA进行求解，说明本文的模型和方法如何用于配网线路的无人机自主巡检。

3.1 确定算法最优参数的正交实验

正交实验是一种确定多个因素和多个水平最佳组合的常用实验方法[26-28]，依据正交性选择部分参数组合进行实验，能够使用较少的实验次数找出最佳的实验条件。

正交实验的第一步是确定影响算法的相关参数及其取值；然后，构建正交表LM(QF)，其中，L表示正交表采用拉丁方法进行构建，M为实验的次数，F为参数的个数，而Q则是每个参数的取值个数；最后，选取若干个数据集，并在正交表中每个参数组合下进行多次实验，并根据实验结果确定最优参数组合。

IGA相关参数有：种群规模NP，交叉概率PC，变异概率PM和迭代次数Iter，通过实验测试并参考相关文献，确定了上述4个参数的取值如表1所示。

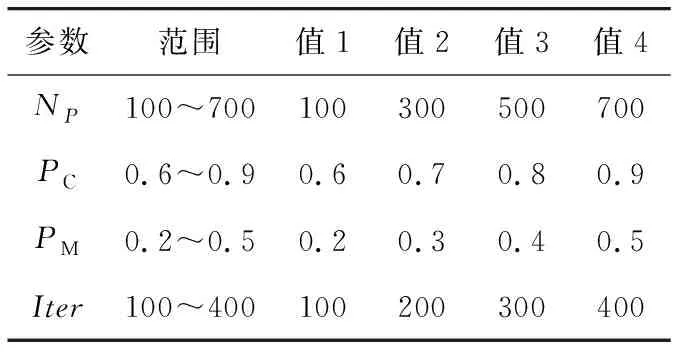
表1 IGA相关参数及其取值Tab.1 Related parameters and their values of IGA

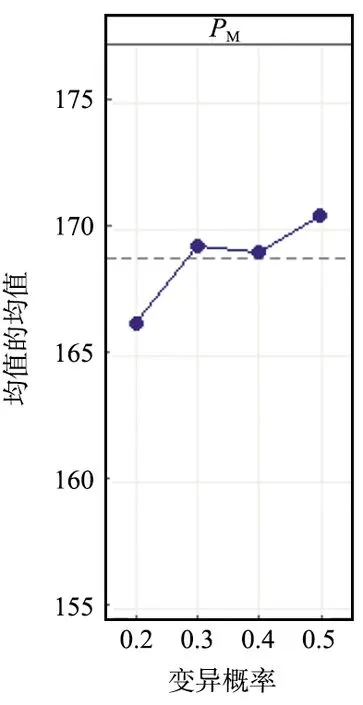
在表1的基础上构建正交表L16(44)，并基于文献[25]中的3个OP基准实例数据集，采用正交实验法对IGA参数进行调优。所选取的数据集为文献[25]中Tmax=30的3个实例，每个实例进行10次重复实验并取平均值，输入Minitab软件得到的参数分析结果如图3所示。

(a) 种群规模均值

(b) 交叉概率均值

(c) 变异概率均值

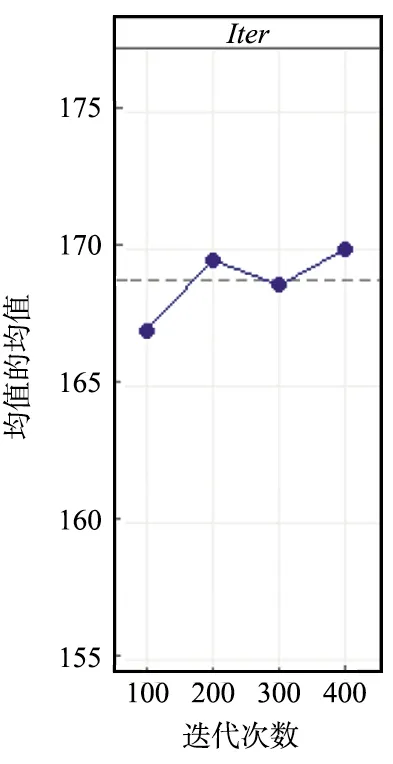
(d) 迭代次数均值图3 正交实验参数分析Fig.3 Analysis diagram of orthogonal experimental parameters

由正交实验的原理以及图3所示的参数分析结果，可以确定IGA的最佳参数组合为：种群规模NP=700，交叉概率PC=0.8，变异概率PM=0.4，迭代次数Iter=400。

3.2 基于OP标准实例数据集的数值实验

为了展示IGA的算法性能，基于小规模和大规模的OP标准实例数据集设计了2组数值实验。所有实验均在3.1节中正交实验确定的最优参数组合下进行。

① 小规模数值实验

使用IGA对文献[25]中的第3组经典OP标准实例数据集进行数值实验，该组数据集的顶点数量n为33。在同组的所有标准实例中，顶点的位置和权重完全相同，只是最大持续时间Tmax不同。使用IGA对每个实例运行10次，并将所求得的最大收益及对应的路径长度记录在表2中。其中，Gap表示IGA求得的解与文献[25]最优解的差距，计算公式为：

(11)

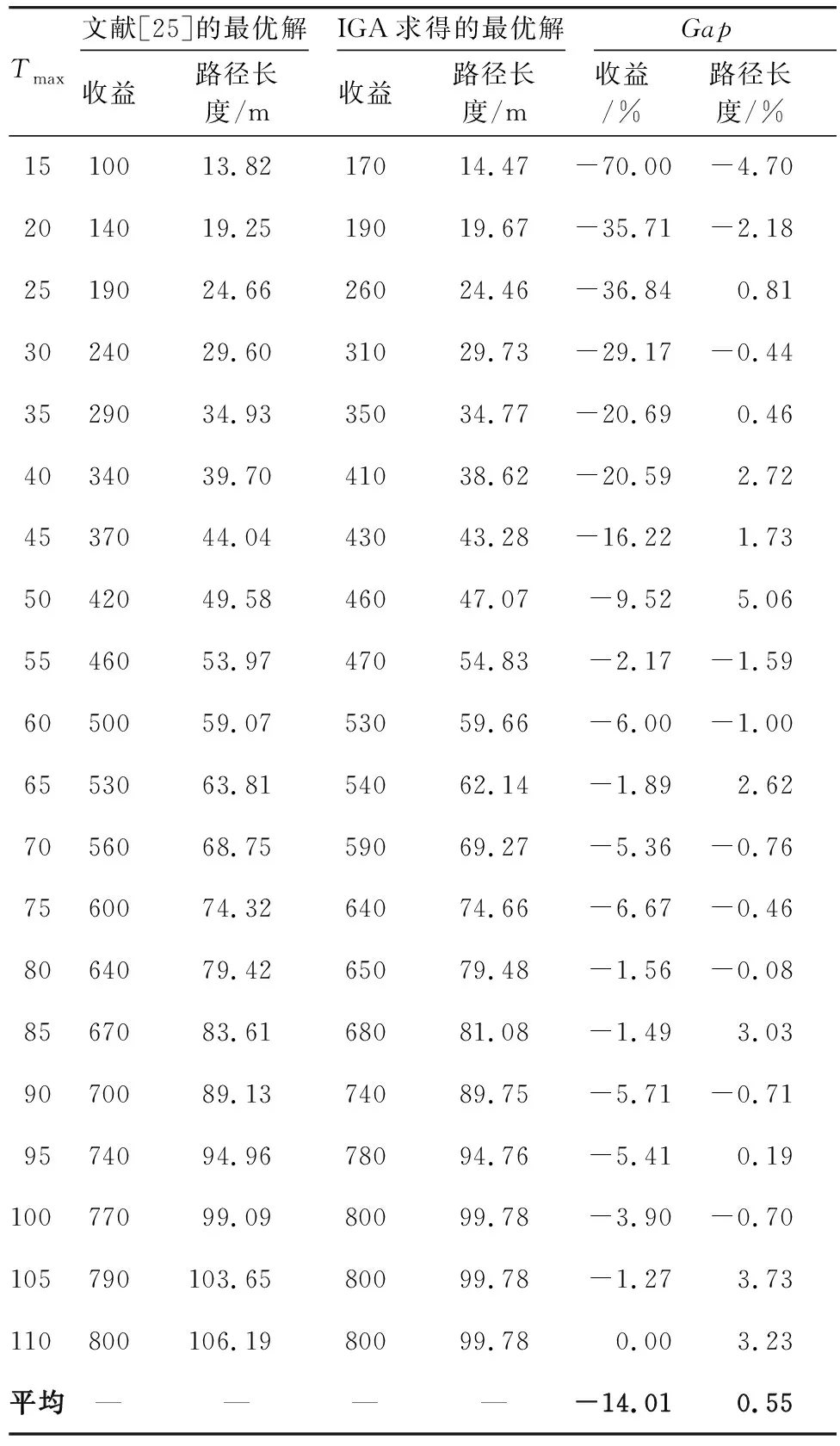
表2 OP标准实例数据集3(33个点)的对比实验结果Tab.2 Comparative experimental results of OP benchmark instance dataset 3 (33 points)

从实验结果可以看出，IGA求得的第3组经典OP基准实例数据集的最优解均优于文献[25]的解，收益的平均Gap为-14.01%，说明IGA求得的收益比文献[25]求得的收益平均提升了14.01%；路径长度的Gap为0.55%，这是因为IGA求得的路径方案访问了更多的节点，可以理解为：IGA用平均0.55%的路径增加换来了14.01%的收益增长。

② 大规模数值实验

使用IGA对文献[29]中的P6经典OP基准实例数据集进行求解，该组数据集的顶点数量n为66。在同组所有标准实例中的顶点位置和权重完全相同，只是最大持续时间Tmax不同。使用IGA对每个实例运行10次，并将所求得的最大收益及算法运行时长记录在表3中。其中，Gap表示IGA求得的解与文献[29]最优解的差距，计算公式为：

(12)

表3 OP标准实例数据集P6(64个点)的对比实验结果Tab.3 Comparative experimental results of OP benchmark instance dataset P6 (66 points)

从实验结果可以看出，除了最后3个实例IGA求得的解比文献[29]中P6经典OP基准实例数据集的最优解稍差，其余11个实例均求得与文献[29]相同的解，收益的平均Gap为0.39%；算法运行时长的平均Gap为77.75%，说明IGA的运行时长远小于文献[29]的算法，可以理解为：IGA以0.39%的收益损失提升了77.75%的算法效率。

3.3 基于脱敏配网线路真实数据的仿真实验

为了说明上述研究工作在现实场景中的应用，基于脱敏的配网线路真实数据进行了仿真实验，仿真场景如图4所示。

图4 无人机自主巡检配网线路场景Fig.4 Scenario of distribution network line inspected by autonomous UAV

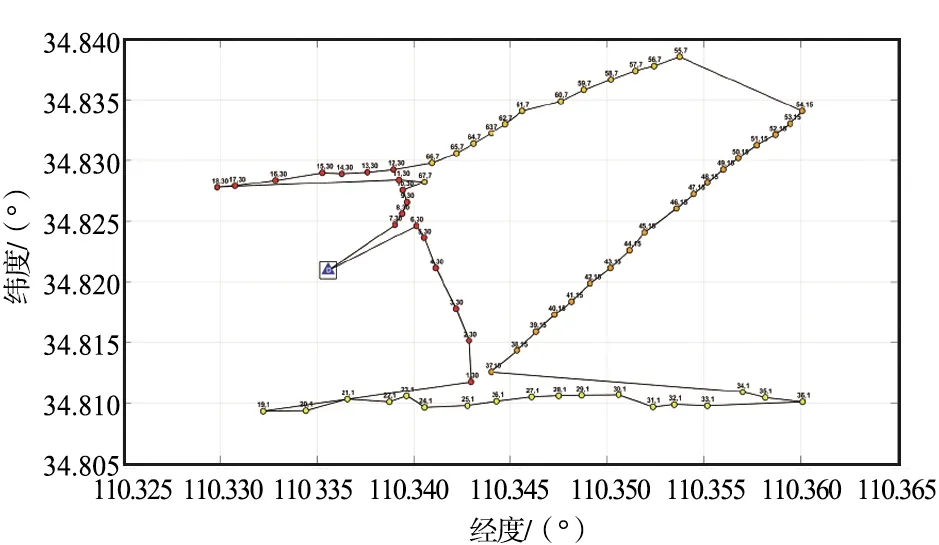
无人机从站点0出发，对配网线路进行自主巡检，共有4条线路、67个杆塔，图中每个点代表一个杆塔。杆塔上方有2个数字，其中，第1个数字是杆塔的编号，第2个数字是杆塔的权重，即该杆塔距离上一次被巡检的时间间隔，时间间隔越长则权重越大，在图4中的颜色也越深。

为了验证不同型号的无人机在不同巡检速度下的巡检效果，设定无人机的续航能力分别为20，25和30 min，并设定无人机的平均巡检速度分别为5，10和15 m/s，组合后得到9组仿真实验，例如，案例(25，15)表示续航时长为25 min，巡检速度为15 m/s。利用TOP模型对上述无人机自主巡检配网线路的任务进行建模，并使用IGA对每个案例求得10次，并将所求得最优解的巡检杆塔数量、路径收益、路径时长和算法运行时长记录在表4中。

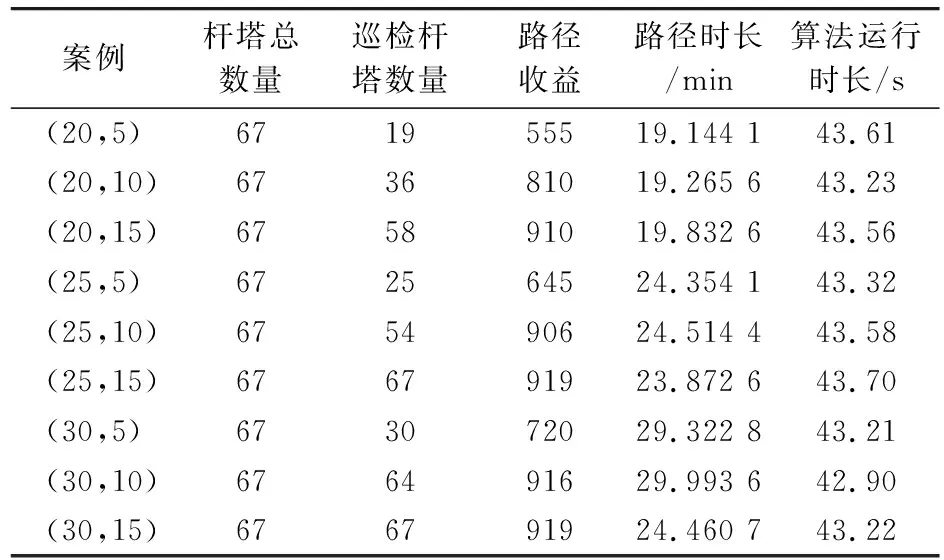
表4 仿真实验结果Tab.4 Simulation experiment results

案例(20，5)的最优巡检路径如图5所示。由图5可以看出，无人机对所有30 d未巡检的杆塔进行了巡检，同时由于续航能力允许，还对15 d未巡检的37#杆塔进行了巡检，但算法求得的最优巡检路径与现实中的巡检方案略有出入。现实中的配网巡检一般以单条线路为单位，无人机从小号杆到大号杆依次进行巡检，这样便于巡检后的内业操作与处理。虽略有出入，但算法可以为实际操作提供参考，大大降低了手动规划巡检路径的工作量。IGA求得的案例(30，15)最优巡检路径如图6(a)所示，从表4中看到该路径的时长为24.460 7 min。而按实际业务需求操作的巡检路径如图6(b)所示，经过计算可知，图6(b)路径的时长为25.342 6 min。实验结果表明，IGA求得的巡检路径方案更优，说明IGA能够有效缩短巡检路径时长，提升巡检效率。

图5 案例(20，5)的最优巡检路径示意Fig.5 Schematic diagram of optimal inspection path in case (20,5)

(a) 算法最优路径

(b) 实际操作路径图6 案例(30，15)的算法最优路径与实际操作路径示意Fig.6 Schematic diagram of optimal path and piratical operation path in case (30,15)

通过对上述9组仿真实验结果进行分析，有以下4个发现：

① 无人机会优先巡检权重较高的杆塔，这符合配网线路巡检的业务需求，即应该对较长时间没有被巡检的杆塔优先巡检。

② 本文提出的IGA稳定性较好，而且可以在合理的时间内求得较优的无人机自主巡检方案，每个案例的路径时长都达到了续航能力的上限，这说明算法求得的巡检方案最大限度地发挥了无人机的效用。

③ 同一型号的无人机执行巡检任务时，飞行速度越快可以巡检的杆塔数量越多；不同型号的无人机执行巡检任务时，续航能力较强的无人机可以巡检更多数量的杆塔。但速度可以弥补续航能力的不足，比如案例(20，10)中虽然无人机的续航能力只有20 min，但如果它以10 m/s的平均速度进行巡检，可以巡检36个杆塔，多于案例(25，5)的25个杆塔和案例(30，5)的30个杆塔。

④ 在案例(20，5)中，无人机仅能巡检1条线路，而在案例(25，15)和案例(30，15)中，无人机能巡检全部的67个杆塔。这符合不同业务场景下的需求，比如日常巡检任务可以由续航能力较短的无人机进行精细化巡检，而在应急场景下，一般使用续航能力较长的无人机快速地对所有线路进行巡检，以便发现线路问题。

4 结束语

本文基于无人机对配网线路进行自主巡检的场景，在考虑无人机续航能力的前提下，构建了以巡检收益最大化为目标的OP模型，并首次将杆塔的巡检间隔时间作为权重，来优化无人机自主巡检的路径。在传统GA的基础上，引入了SA算法的Metropolis准则，以提升遗传算法的局部搜索能力，仿真实验表明，IGA可以求得大部分经典OP基准实例数据集的最优解。IGA还可以应用于无人机自主巡检的实际场景中，并可以在合理的运行时间内求得较优的无人机自主巡检方案。在未来的研究中，将关注多无人机协同进行自主巡检的场景，同时，除了杆塔的巡检任务，还会关注杆塔之间线路通道的巡检任务。