连续退火炉快冷段非均匀气体射流冲击换热特性研究
2022-06-29朱金琪李泽琳豆瑞锋胡志远
朱金琪,李泽琳,王 磊,豆瑞锋, 3,谢 宇,胡志远,温 治, 3,马 琳
(1.北京科技大学 能源与环境工程学院,北京 100083; 2.首钢智新迁安电磁材料有限公司,迁安 064400;3.冶金工业节能减排北京市重点实验室,北京 100083)
硅钢是一种Fe-Si软磁合金材料,又称电工钢或电磁钢,是电能和磁能进行最有效地交换能量的功能材料[1]。无取向硅钢具有高磁感、低铁损的特点,常被用作马达和发电机的铁心[2]。无取向硅钢不仅要求磁性能好,而且要求尺寸精度高。在无取向硅钢生产过程中,经常会出现板形不良问题,且由于硅钢产品所特有的磁性需求,不能采用诸如平整、拉矫等常规工艺改善浪形问题,因此控制和改善硅钢板形存在极大的难度[3]。冷轧硅钢连续退火热处理过程中,如果带钢宽度方向温度不均匀,将会使得带钢产生浪形,降低带钢形状精度。宽度方向冷却均匀性是影响板形的重要因素[4],为了解决板形问题,就必须实现带钢温度的准确控制[5]。张修成通过增加循环冷却风机的输出量,调整循环冷却水温到45 ℃,以降低冷却速度的方式实现炉内带钢温度的调控。马云龙[6]通过减少带钢边部冷却氮气通入量,增加二肋(两侧)氮气通入量,将冷却循环气路的闸板由原来的2-5-9-5-2调整到1-6-9-6-1,即通过调整带钢宽度方向冷却能力的方式实现对板温的控制。
首钢迁钢在无取向硅钢连退机组的快冷段,通过对带钢宽度方向不同位置处喷嘴射流速度的调节,实现带钢宽度方向换热强度的调控,进而实现对带钢温度的精准控制。但是,由于相邻喷嘴存在射流速度差,为非均匀气体射流冲击换热过程,相邻射流之间存在复杂的相互影响,现有的多喷嘴均匀气体射流冲击换热特性经验公式[7-13],无法对其换热特性进行准确的计算。
本文基于数值模拟[14-19],针对连续退火炉快冷段气体射流冲击换热过程,在相邻喷嘴存在射流速度差的情况下,开展多喷嘴非均匀气体射流换热特性研究。
1 冷却段风箱结构与数学模型的建立
无取向硅钢连续退火快速冷却段风箱结构如图1所示。风箱由五个独立的风道组成,各个风道沿带钢宽度方向平行布置,风箱的底部采用叉排形式布置扩口型喷嘴。每个风道有独立的风道闸门控制,冷却气体经扩口型喷嘴流出,形成气体射流,冲击到无取向硅钢表面,实现带钢的快速冷却。

图1 冷却段风箱结构示意图
针对实际的风箱结构,数学模型中,仅保留主要部分:喷口、带钢。在数学模型中,忽略风箱内部的气体流动,认为同一组扩口型喷嘴的射流速度是一致的。数学模型的几何结构如图2所示,喷箱部分仅保留喷孔结构。数学模型中,直接设置喷嘴入口速度,从而实现风速的调节。

图2 多喷嘴换热模型几何结构
在多喷嘴气体射流冲击换热数值模拟模型中,采用Transition SST模型[20]模拟湍流流动。如图2所示,在模型中,底部靶面(带钢)设定为定壁温边界条件;侧面设置为压力出口条件;喷嘴设置为速度入口条件;其它表面均为绝热边界条件。
计算网格绘制中,在喷嘴处与靶面附近,对网格进行了局部加密,用以提高计算的准确性。模型网格总数为686万。本文所有仿真结果均为网格独立解。
在无取向硅钢连续退火生产过程中,为了实现对带钢温度的控制,通过风道闸门,控制各个风道的循环气体流量不同,进而使得不同风道的喷嘴,其气体射流速度存在差异。根据现场的风机型号、风道结构以及风道阀门特性[21],开展多喷嘴气体射流冲击换热特性研究。为了全面覆盖现场实际工况,设置:中间风道喷嘴出口流速度为20~100 m/s,边风道和肋风道的喷嘴出口流速度为0~100 m/s。模拟计算了总计62种工况下的换热特性分布规律。
2 数据分析方法
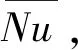
(1)
在多喷嘴气体射流冲击换热研究中,定义ReRatio如式(2)所示,其中ReM为中间风道喷嘴出口雷诺数,ReR为肋风道喷嘴出口雷诺数。在本文的研究中,相邻喷嘴射流速度差异主要存在于中间风道和肋风道之间,而肋风道与边风道的喷嘴之间不存在射流速度差异,因此对于ReRatio的定义,仅包含中间风道与肋风道的雷诺数。
ReRatio=ReM/ReR
(2)
在带钢宽度方向上定义无量纲距离L,如式(3)所示。
L=x/D
(3)
式中:x为带钢宽度方向任意一点与参考线(通常为对称线)的距离,m;D为喷嘴直径,m。
3 模拟结果分析及经验公式的拟合
根据多喷嘴风箱结构的对称性,将对流换热努塞尔数沿带钢宽度方向上的对称线进行对称平均,用以减少计算本身所带来的数据波动。
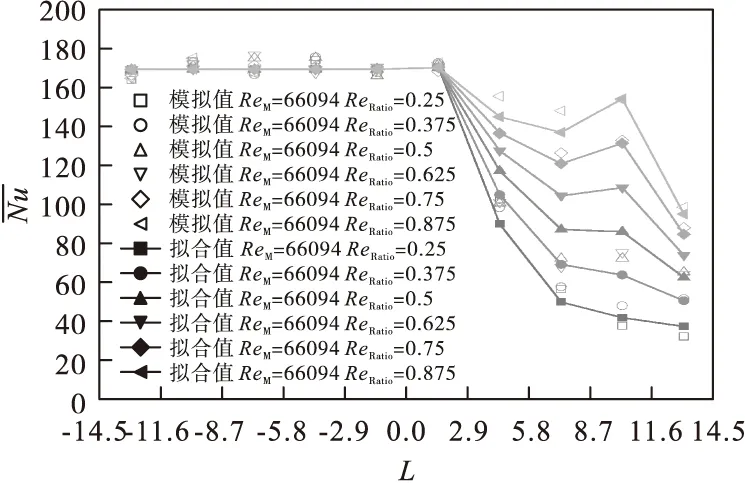
以中间风道射流速度为40 m/s时的工况为例,阐述非均匀气体射流冲击换热特性的数据处理方法。首先,建立坐标系,坐标原点建立在对称中心线上。然后,将带钢沿着宽度方向划分n份,采用式(1)计算每一份的平均努塞尔数,获得多喷嘴非均匀气体射流冲击换热平均努塞尔数随宽度的变化特性,结果如图3所示。最后,根据平均努塞尔数的变化规律,分区域进行分析,将平均努塞尔数的变化分为中心区与非中心区,非中心区包括变化区、均匀区、边缘区,如图3所示。

图3 中间风道射流流速为40 m/s,ReM为66 094时换热特性分布
采用共轭梯度法[22],对所得数据进行分段拟合。如式(4)所示,为中心区平均努塞尔数与射流雷诺数ReM的关系,适用范围为ReM∈(24 785,165 235)。
(4)

图4 中心区换热特性经验公式拟合图
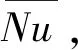

图5 ReRatio≤0.25,ReM∈[66 094,82 618],中心区模拟值与拟合值对比图
(5)
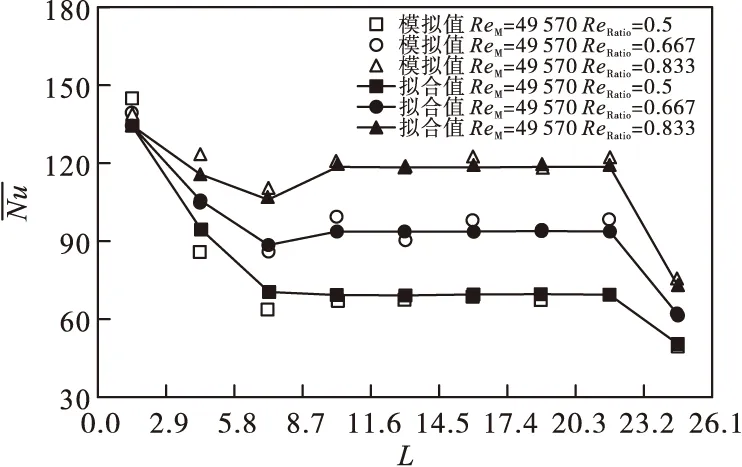
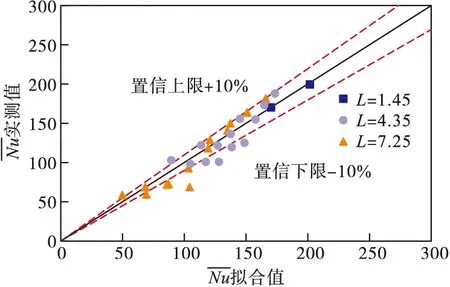
当0.25 (6) (7) (8) 变化区内换热性能,经式(6)~式(8)计算所得拟合值与模拟值进行对比,设置置信区间为0.9,结果如图6所示。 图6 变化区拟合公式置信区间(1-α=0.9) 由图6可以发现,绝大部分的实测值都在拟合值的置信区间内,表明拟合公式(6)~式(8)是可靠的,可以实现对变化区内换热特性的有效预测。 均匀区内相邻喷嘴射流速度相同,换热特性如式(9)所示。 (9) 边缘区换热特性与均匀区有明显差异,其换热特性如式(10)所示。 (10) 通过式(6)~式(10)对0.25 以中间风道射流速度为40 m/s工况为例,其仿真模拟值与经验公式拟合值的对比如图7所示。均匀区平均误差为2.72%,边缘区平均误差为2.85%。ReRatio>0.25时,经验公式拟合值与模拟值的拟合很好,其平均误差为4.38%。通过分段拟合的方法,实现了叉排结构多喷嘴圆孔射流换热过程中,相邻喷嘴射流存在速度差时,多喷嘴非均匀气体射流换热特性变化的定量化表达。 图7 ReRatio>0.25,ReM=49 570,非中心区模拟值与拟合值对比图 变化区换热特性的预测,是多喷嘴非均匀气体射流冲击换热特性研究过程中的重点和难点。喷嘴结构与排布方式相似、射流速度发生变化时,通过经验公式(6)~式(8),依旧能实现对变化区换热特性的预测。本节对变化区所得经验公式进行数值模拟验证。在验证性模拟计算中,设置中间风道与肋风道射流速度一致,射流速度范围40~50 m/s;边风道与肋风道间存在射流速度差,边风道射流速度范围10~45 m/s。 在模拟验证检验中,在无量纲位置L为1.45、4.35、7.25时,经式(6)~式(8)计算所得拟合值与模拟值进行对比,结果如图8所示,图8中置信区间为0.9。尽管射流排布方式发生了变化,但是拟合得到的经验公式,依旧能够很好的预测换热特性的分布规律。 图8 变化区拟合值与模拟值进行对比 在非均匀气体射流冲击换热验证中,ReRatio均大于0.25,故经变化区换热特性经验公式(6)~式(8),均匀区换热特性经验公式(9),边缘区换热特性经验公式(10),对整个靶面不同区域内的换热特性进行计算与验证。当ReM、ReR为66 094(射流速度40 m/s)与82 617(射流速度50 m/s)时,不同ReRatio条件下,改变风箱射流速度分布,仅在肋风道和边风道之间存在射流速度差异,获得多喷嘴非均匀气体射流冲击换热特性分规律,模拟值和拟合值(拟合公式计算值)的对比如图9、图10所示。 图9 ReM与ReR都为66 094时换热特性分布规律对比验证 图10 ReM与ReR都为82 617时换热特性分布规律对比验证 如图9、图10所示,在对比验证中,尽管射流速度差异所在位置发生了变化(肋风道和边风道之间),通过多喷嘴非均匀气体射流换热经验公式(式(6)~式(10)),依然能够实现对其换热特性的有效预测。 对比验证证明,通过分段拟合的方式,有效地解决了相邻喷嘴射流速度存在差异时,气体射流冲击换热特性变化趋势的定量化表达,拟合所得无量纲经验公式,具有普适性意义。 本文针对多喷嘴非均匀气体射流冲击换热现象,采用CFD数值模拟的方法,获得换热规律;通过分段拟合的方式,实现其换热特性的定量化表达。变化区换热特性的研究结果,具有普适性意义。在喷嘴结构及其排布方式相似时,即便各个喷嘴射流速度的分布发生了变化,其换热特性依然能够通过经验公式(6)~式(10)进行计算。 本文为非均匀气体射流冲击换热特性的分析,提供了具有通用性的分析方法。通过该方法,可以分析其他类型阵列喷嘴的非均匀气体射流冲击换热。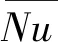

4 经验公式验证

5 总 结
