“问题提出”，实现思维水平的多重提升——以“百分数变化幅度问题”的教学为例

浙江省杭州市萧山区瓜沥镇坎山小学 李 青

“百分数变化幅度问题”是人教版数学六年级上册 “百分数（一）”的一个学习内容，具有一定的综合性，是对本单元百分数相关知识的综合性运用。到了六年级，学生完全有能力、也有意愿去探索和研究数学问题。为此，教师采用“问题提出”教学模式，放手让学生自主提问、独立探究、交流互动，以此达成教学目标，并促使学生用整体的眼光研究同类问题，提升学生的“问题提出”能力和数学思维水平。

一、数学分析

教材中的“百分数变化幅度问题”具体为“某种商品4月末的价格比3月末降了20%，5月末的价格比4月末又涨了20%。5月末的价格和3月末比是涨了还是降了？变化幅度是多少？”这是“连续求一个数增、减百分之几”的问题，可以用“□×（1－□%）×（1＋□%）”的形式表示，是“求比一个数多（少）百分之几是多少？”和“求一个数比另一个数多（少）百分之几”问题的综合运用。此类题型还可以衍生出“先增后减”“连续增加百分之几”“连续减少百分之几”“如何增减才能回到原价”等多种问题。教学时，教师应以教材问题为基础，引导学生在此基础上不断提出新问题、发现新规律。

二、教学分析

“百分数变化幅度问题”的难点在于，作为初始单位“1”的3月份是个未知量，同时，连续增减变化，单位“1”也会随之变化。并且，这一问题具有一定的综合性。从不同的角度观察，我们可以得到不同的记录。在教学中，教师不能满足于得出一个问题的结果，而应从重视变化结果转变为关注变化过程，使学生能举一反三解决同类型问题并发现其中包含的规律。

因此，本堂课的主要教学环节分为：

1.提供情境引出研究内容，并引导学生提出“分步和综合”两种问题，为局部和整体研究此类问题提供素材。

2.学生解决两种问题，并在交流汇报的过程中，体会此类问题中包含的“变与不变”的规律。

3.在解决基本问题的基础上，鼓励学生提出更多相似的问题，从而对一类问题的解决方法及其所包含的规律进行整体研究。

三、教学实践

（一）情境导入，提出问题

课始，教师给出与百分数有关的问题情境，请学生提出问题，根据提问情况引出本堂课的研究内容。

师：同学们都有自己喜欢的书籍吧。月月非常喜欢《奇妙的数学世界》，她一直关注着这套书的价格。这套书“4月的价格比3月降了20%，5月的价格比4月又涨了20%”。看到这些信息，你能提出哪些数学问题？可以是简单的，也可以是稍复杂的。

生1：4月份的价格是3月份价格的百分之几？

生2：5月份的价格是4月份价格的百分之几？

生3：5月份的价格是3月份价格的百分之几？

生4：5月份的价格是不是和3月份的价格相同？

师：同学们提的问题都非常好，请你大胆猜想一下，这套书5月份的价格会等于3月份的价格吗？

生5：我觉得是一样的，4月份价格先降了20%，5月份价格又涨了20%，相互抵消了。

生6：我觉得不一定，4月份降的20%和5月份涨的20%不一样，也就是单位“1”不一样。

师：两位同学的说法，似乎都有道理。今天这节课，我们就来研究“变化幅度”问题。

【设计意图：学生根据教师给出的信息，结合自己的实际水平，提出了涉及部分信息的问题和综合性问题。这两类问题将在后续的深入分析问题和整体呈现规律等两方面发挥重要作用。】

（二）解决问题，比较沟通

在学生提出两类问题之后，教师组织学生独立解决问题，并在此基础上通过局部与整体的比较、辨析，引导学生发现“百分数变化幅度问题”中包含的规律。

师：要研究5月份的价格与3月份的价格的关系，同学们提的前两个问题有没有用？（生1和生2）

生：有用的，因为题目中没有告诉我们5月份的价格和3月份的价格是什么关系，我们必须要算出4月份的价格。

师：是的，所以前面两个问题合起来，就组成了第3个、第4个问题。那现在我们可以解决这些问题了吗？

生1：还有一个问题，3月份的价格还不知道，那就没法算4月份的价格，也没法算5月份的价格。

生2：可以假设一个数字。

生3：也可以直接用单位“1”来表示。

师：那就请大家自己试一试吧。

（学生独立尝试解决问题后汇报交流）

生1：我是假设3月份的价格为200元，那么，4月份的价格就是200×（1-20%）=160（元），5月份的价格是160×（1＋20%）=192（元），5月份的价格比3月份的价格少了。

生2：我是假设3月份的价格是100元，然后，4月份就是80元，5月份是96元，5月份的价格也比3月份的价格降了。

生3：我是用字母表示的，假设3月份的价格是a元，4月份的价格是a×（1－20%）=0.8a（元），5月份的价格是0.8a×（1+20%）=0.96a（元）。

生4：用单位“1”表示也差不多，3月份价格是单位“1”，4月份的价格就是0.8，5月份的价格就是0.96。

师：这几位同学的做法都是怎么解决的？

生5：都是假设3月份的价格，因为只有知道3月份的价格，才能继续算其他月份的价格。

生6：根据3月份的价格，都是先算4月份的价格，再算5月份的价格。

师：有没有同学能把这些方法列成综合算式？

（学生说综合算式，教师板书记录）

师：从这些综合算式（见图1）中，我们可以发现哪些信息呢？

图1

生1：5月份的价格都比3月份的价格少了，192比200少，96比100少，0.96a比a少，0.96比1少。

生2：我发现不管设3月份的价格是多少，后面都要经过相同的计算。也就是说，都要先算出3月份价格的80%，得到4月份的价格，再算4月份价格的120%，得到5月份的价格。

生3：我们可以把两次运算合起来看，简单地说，就是先降20%得到80%，再涨20%，得到120%。

生4：补充一下，这个120%不是3月份价格的120%，而是4月份价格的120%，那么就相当于3月份价格的96%。因为先得到80%，再乘120%，最后是96%。

生5：他的意思是，可以先算后面两次变化。那么，5月份价格=3月份价格×（1－20%）×（1＋20%）=3月份价格×96%。

师：这几位同学的发现非常重要，从他们的发现里，你可以得到怎样的结论？

生：我发现不管假设3月份的价格为多少，5月份的价格总是它的96%，那么，总是比3月份的价格下降1－96%=4%, 下降了4%。

师：同学们，刚才我们提出了不同的问题，有分步计算的问题，也有列综合算式解决的问题，你觉得分步算好还是综合算好？

生1：综合的好，综合的方便我们比较，发现5月份的价格只有3月份价格的96%。

生2：分步的也有优点，没有分步的，我一下子写不出综合算式。而且，分步的问题也让我知道了4月份的价格是多少。

生3：通过分步算式，我知道了单位“1”是在变化的。求4月份的价格时，单位“1”是3月份的价格，求5月份的价格时，单位“1”是4月份的价格。因此，不能简单地看到先降20%再涨20%，就以为价格不变了。

师：同学们对这类问题分析得非常到位，评价也很合理，太好了。

【设计意图：学生通过分步计算，解决了实际问题，发现用不同的方法解决，5月份的价格都比3月份的价格要小。在此基础上，教师呈现综合算式，组织学生观察、发现算式中隐藏的规律：不管怎么算，5月份的价格总是3月份价格的96%。随后，教师组织学生对自己提出的分步和综合两类问题的作用进行比较，使学生发现这两类问题各有自己的价值，前者能帮助我们更好地运用知识、解决问题，后者有利于我们发现其中的规律。】

（三）“问题提出”，拓展延伸

在研究例题的基础上，教师鼓励学生自己提出问题，通过“问题提出”考查学生对此类问题的理解程度。

师：刚才，我们提出了分步和综合的两类问题，在解决问题的过程中，发现了价格变化幅度问题的规律。你能不能试着自己提出一个类似的问题？

生1：商场里搞促销，一台电视机先降价20%，促销结束后又涨价20%。现在价格和原来比是贵了还是便宜了？

生2：冬天快到了，一款羽绒衣涨价了20%，到了春天，又降价20%。这款羽绒衣比原价贵了还是便宜了？

生3：我也是电视机，但是，我是先降价10%，再涨价10%，问贵了还是便宜了？

生4：一台洗衣机，先降价20%，再上涨百分之几才能回到原价？

生5：如果是连续涨20%，5月份的价格与3月份的价格比相差多少？如果是连续降价20%，5月份的价格和3月份的价格相比，相差多少？

师：太精彩了，同学们不但提出了和课本上类似的问题，还提出了很多新问题。我们先来研究哪一个呢？

生6：第一个问题和刚才的例题是一样的，所以我不研究了。我想研究先涨价再降价的问题，因为这个问题的过程和例题刚好相反。

生7：我想研究降价10%再涨价10%的问题，我想看看百分数变了，是不是还是一样的结果。

生8：连续降价肯定比原价低，连续涨价也肯定比原价高，但是相差多少，还是可以研究的。

生9：洗衣机先降价20%，再涨多少的问题有点复杂，但我想试试。

（学生解答自己感兴趣的问题后，在全班交流）

1.研究“先涨20%再降20%”的问题

生：我是假设羽绒衣的价格为单位“1”，1×（1+20%）×（1-20%）=0.96=96%。我发现和先降再涨是一样的。

师：怎么会这样呢？两种不同的算法，4月份的价格是不一样的啊？

生1：“先涨再降”是先乘120%再乘80%，“先降后涨”是先乘80%再乘120%，不管先后顺序，最终都是原价的96%，和先降20%再涨20%一样。

结合学生的回答，教师完成完整板书：

先涨再降：1×（1+20%）×（1-20%）=1×96%=0.96

先降再涨：1×（1-20%）×（1+20%）=1×96%=0.96

生2：根据乘法交换律，先乘80%或先乘120%，结果都是一样的。

2.研究“先降10%再涨10%”的问题

师：刚才有一个问题，是把20%都换成了10%，谁解决了这个问题？

生1：改成10%的话，那就是1×（1－10%）×（1＋10%）=0.99，也就是99%，还是便宜了。

生2：我发现改成先涨10%再降10%，也是一样的，因为只是交换了一下运算顺序。

生3：我自己又把10%改成了30%试了一下，1×（1－30%）×（1＋30%）=91%，还是降了。

师：这个尝试非常好，我们把10%、20%、30%联系起来看一下，你有什么发现？（见图2）

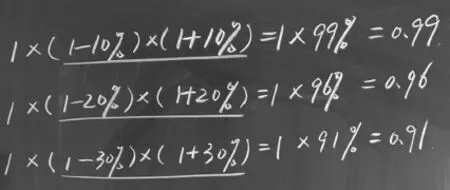
图2

生1：不管是百分之几，也不管是先涨后降，还是先降后涨，都比原来要便宜。

生2：而且，这个百分数越大，最后就越便宜。

生3：涨和降必须是同一个百分数，比方说，都是10%，或都是20%。

师：大家观察得很仔细，最后这个意见非常严谨，确实是这样的。

3.研究“先降20%再涨（ ）%才能回到原价”

师：刚才还有一个问题，先降20%，然后要回到原价，你怎么看？

生1：那肯定不可能是涨20%了。

生2：要比20%大一点。

生3：我刚才选的就是这个问题。先降20%，那就是0.8，然后要回到原价，就是回到单位“1”，所以，我只要用单位“1”除以0.8就行了，得到1.25，也就是125%，那么就是再涨25%。

师：按照你的方法，算式应该是1÷（1－20%）－1=25%。我们也可以把25%放到乘法算式中验算一下：“1×（1－20%）×（1＋25%）”，回到原价了吗？

生：1×（1-20%）×（1+25%）=1×80%×125%=1×1=1，是原价。

师：按照他的方法，我们还可以研究先降10%，再涨百分之几，可以回到原价的问题，当然也可以研究其他百分数，这个问题我们课后再去研究。

【设计意图：在提问的过程中，一部分学生模仿例题对所学知识进行了运用，更多的学生则在原有的基础上进行了发散性思考，提出了包含更多变化的新问题。这些问题的提出和解决，使学生对此类问题有了新的认识和更深的理解。学生的“问题提出”和数学思考能力得到了进一步的发展。】

四、教学反思

本堂课的教学过程，充分体现了“问题提出”教学模式对学生数学学习、情感态度和数学思考等方面的价值。

（一）创设恰当的情境鼓励学生提出问题

“问题提出”教学模式的目的是给学生创造更多的学习机会，鼓励更多的学生参与学习活动。因此，教师应重视不同层次学生的课堂表现，在课堂教学之初，应该降低学习的门槛，让更多学生参与进来。教师请学生根据情境，提出简单的或稍复杂的问题，这有利于不同水平的学生提出符合自身认知的问题。因此，学生提出了分步和综合两种问题，一方面，分步问题分解了学习难点，使学生得以运用所学知识解决问题；另一方面，综合问题有利于学生从整体的视角观察和审视问题中包含的规律。

在学生解决基本问题之后，教师再次鼓励学生提出类似的问题。这既为学生运用刚得出的方法提供了机会，也为提出和研究新问题创造了条件。学生在第一次提问活动的激励下，进行发散性的思考，提出了三种新的问题，为进一步研究这类问题提供了优质的素材。

（二）提出不同层次的问题推动思维发展

在整个教学活动中，学生提出问题的思维水平层层递增。从分步问题到综合问题再到变式问题，最后提出发散性问题，学生在解决这些问题的过程中，对“百分数变化幅度问题”的认识，经历了计算问题的结果到研究解答的过程，再到同类型问题的举一反三和归纳整理的过程。在这一过程中，学生不仅掌握了研究此类问题的方法，在变式运用中提高了对问题本质的理解，而且提升了自己的思维水平，在研究问题的方法、策略等方面也积累了相关的经验。

因此，可以说，“问题提出”教学模式激发了学生研究数学问题的强烈愿望，并为研究提供了一条清晰的路径，对学生数学学科素养的进一步发展起到了重要的作用。