离心选矿系统模糊解耦PID设计*
2022-06-28罗小燕吴庆龄
罗小燕, 吴庆龄, 倪 俊, 刘 鑫
(1.江西理工大学 机电工程学院,江西 赣州 341000; 2.江西省机电设备招标有限公司,江西 赣州 341000)
0 引 言
随着矿山资源的不断开采,现代矿山不得不面对日益贫、细、杂的矿物和长期堆积的数以亿吨的尾矿[1,2]。重选是借助有用矿物和脉石之间的密度差异而实现分选的一种选矿方法[3]。近年来,选矿工作者对重选设备进行了大量的研究和实践,许多新型高效的重选设备相继问世,并取得实际工业生产和运用。
陶有俊等人借助计算机模拟与实验结合的方法发现离心选矿机内部多相流场存在一种水力流态效应,在此基础上得出不同粒度颗粒的分布规律,并以此设计出圆弧形槽口,加速了重颗粒矿物的沉积[4]。朱向楠等人通过图像分析法研究了细粒煤中矿物质的嵌布规律,采用浮选和Faclon对碎后产物进行解离式分选,以此提高重选的精煤产率[5]。以上研究虽然能确定离心选矿机内部颗粒与流体的动态运动特性,但在提高选矿富集比和控制精度上还需进一步优化。
本文拟设计一种模糊解耦比例—积分—微分(proportion integration differentiation,PID)控制算法的智能控制系统,并引入自适应粒子群优化(adaptive particle swarm optimization,APSO)算法对模糊控制器的隶属度函数形状参数进行优化,为离心选矿机的复杂选矿环节提供一种更优的控制方式。
1 选矿系统动态分析
离心选矿过程是二输入二输出的强耦合系统[6],将固体给料量和给水量作为给矿环节中的输入量,给矿流量和给矿质量分数作为输出量,其工作特性可表示为
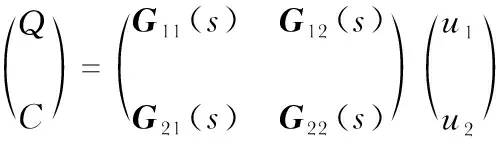
(1)
式中Q和C为输出量,分别为给矿流量和给矿质量分数;u1和u2为输入量,分别为给水量和固体给料量;G为传递函数矩阵。
分析该模型可知,离心选矿动态过程复杂[7,8]。因此,本文将模糊解耦控制[9]应用到离心选矿动态系统中[10],将复杂的强耦合系统解耦为两个独立的单输入单输出系统,以实现给水量直接控制给矿流量,固体给料量直接控制给矿质量分数的目标。
2 模糊PID控制器的设计
离心选矿过程的模糊PID控制器结构原理图如图1所示,包括输入量的初始值设定、参数模糊化处理、模糊规则推理、模糊量精确化以及系统的输出。
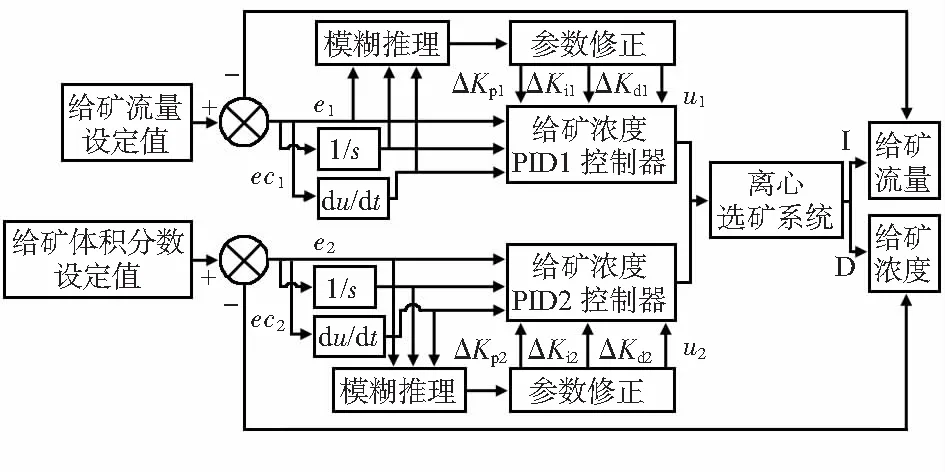
图1 离心选矿过程模糊PID结构原理
首先,对输入控制量的偏差及其偏差变化率进行模糊化处理,得到对应输入参数的模糊量;其次,利用模糊推理将其转换成控制器所能识别的语言变量;最后,由模糊判决输出PID的三个控制变量增量值作为系统控制器的输入量,完成模糊PID控制器3个参数的自整定。
3 基于APSO算法优化的模糊PID控制器
3.1 APSO算法
算法基本原理如下:定义在D维空间内共有N个粒子,粒子所在的位置为Xi=[Xi1,Xi2,…,Xin],飞行速度为V1=[Vi1,Vi2,…,Vin],由目标函数计算得出粒子的适应度值,数值大小决定粒子的好坏程度,空间内的粒子通过不断迭代来寻优,迭代过程中每个粒子都将根据两个“极值”(局部最优解pbest,全局最优解gbest)来更新自己的位置,粒子群算法的速度和位置更新公式为
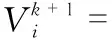
(2)
(3)
式中i=1,2,3,…,n为群体的粒子数;Xi为粒子的空间位置;Vi为粒子的速度;pbest,gbest分别为局部最优解、全局最优解;c1,c2为学习因子;r1,r2为加速因子,为[0,1]内的随机数;w为惯性因子;k为迭代次数。
考虑到传统PSO算法针对实际问题时难以快速较快且精准的寻得最优解,故采用APSO的方法寻优,系数公式为
(4)
式中wmin,wmax为惯性权重的最小值、最大值;f为当前粒子的适应值;fmin为当前粒子群适应值的最小值;fave为当前粒子群适应值的平均值。
3.2 模糊PID控制器参数优化
为了得到更好的控制效果,可通过APSO算法进行优化[11,12]。选用ITEA作为误差性能的指标,该指标能够减小系统的超调量和调节时间,函数公式如下
(5)
3.3 仿真与结果分析
基于APSO算法优化模糊PID 控制器参数的过程分为三部分:1)用MATLAB中m文件编写的APSO程序;2)编写APSO程序和Simulink仿真模型互相连接的程序;3)Simulink仿真模型建立。
图2为Simulink的仿真总图,里面包含了各个模块。
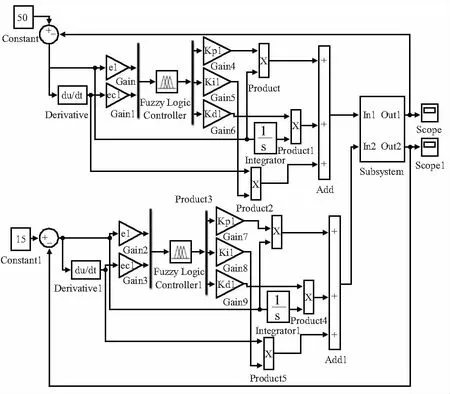
图2 Simulink仿真总图
为了比较APSO算法优化效果,将常规PID、模糊PID、APSO优化的模糊 PID三者结合在一起分析对比。系统响应曲线如图3、图4所示。
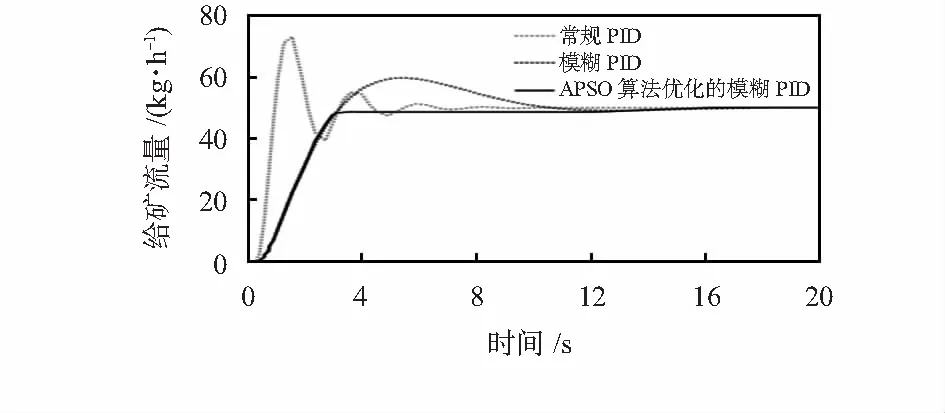
图3 给矿流量响应曲线
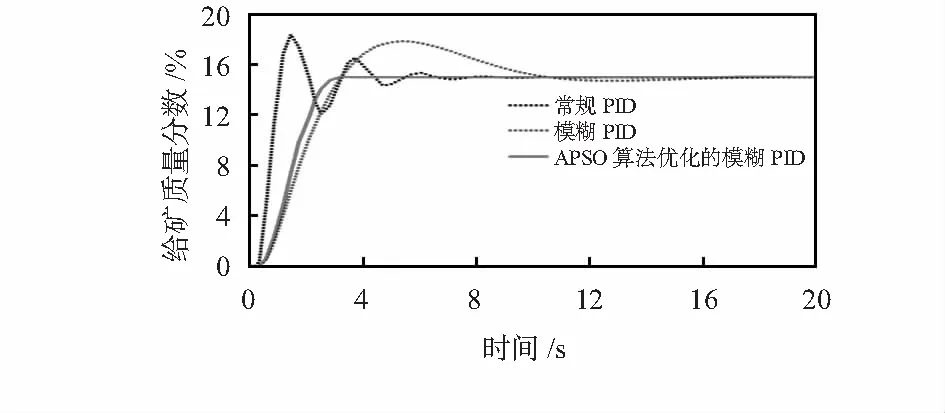
图4 给矿质量分数响应曲线
由图3、图4可知,给矿流量在10~20 s内达到稳态,而给矿质量分数则到达稳态时间更长;而相对于常规PID算法和模糊PID控制算法,本文提出的APSO优化的模糊PID控制算法响应速度更快,曲线变化较平缓,且拥有更短的调节时间。由此可得,本文提出的APSO优化的模糊PID控制算法性能更优。
4 实验验证
为验证本文所设计的基于APSO算法优化的模糊PID控制器对离心选矿系统选矿效果的影响,将常规PID控制器、模糊PID控制器和APSO优化的模糊PID控制器分别应用于本课题组采购的型号为KCXD20的Knelson离心选矿机中进行实验。
4.1 实验方案
根据总结现场经验和传感器所测数据可知,Knelson离心选矿机给矿环节反冲水流量为70 L/min,分选锥转速为710 r/min[13]。实验方案如表1和表2所示。
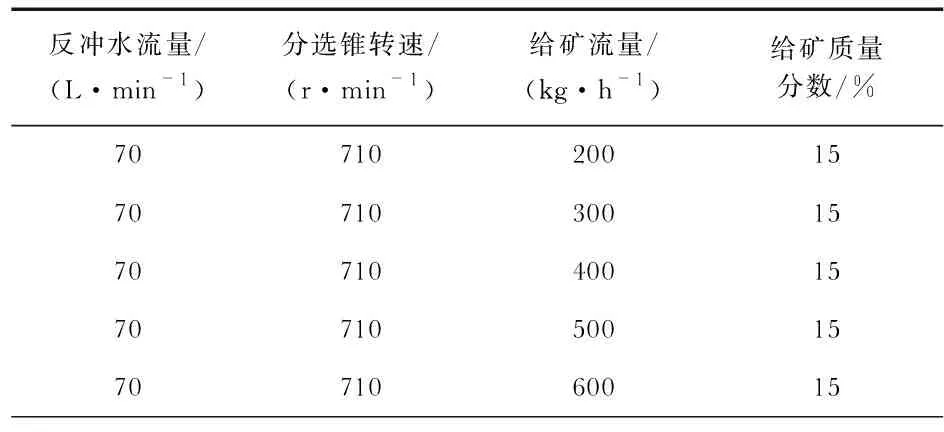
表1 给矿流量因素实验方案
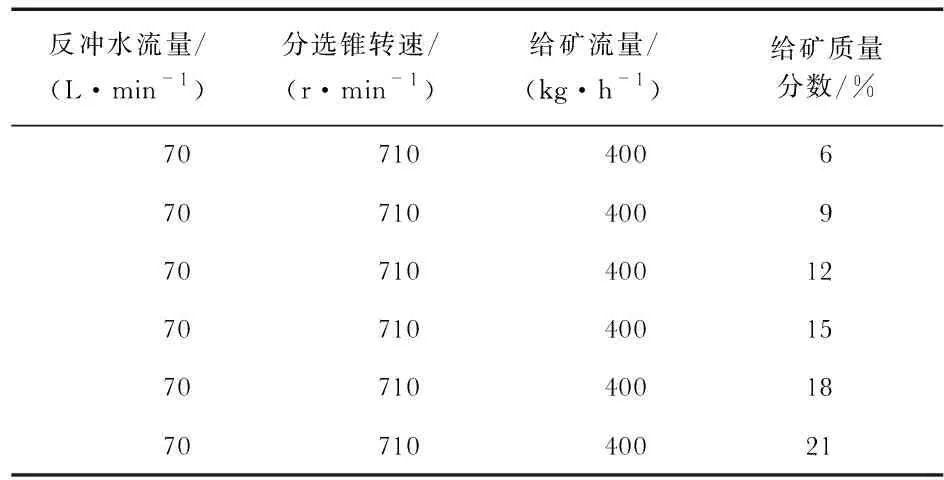
表2 给矿质量分数因素实验方案
4.2 实验结果与分析
依据表1和表2,分别对给矿流量和给矿质量分数进行单变量实验,得到使用常规PID控制器、模糊PID控制器和APSO优化的模糊 PID控制器时,这三者的富集比情况,如图5和图6所示。
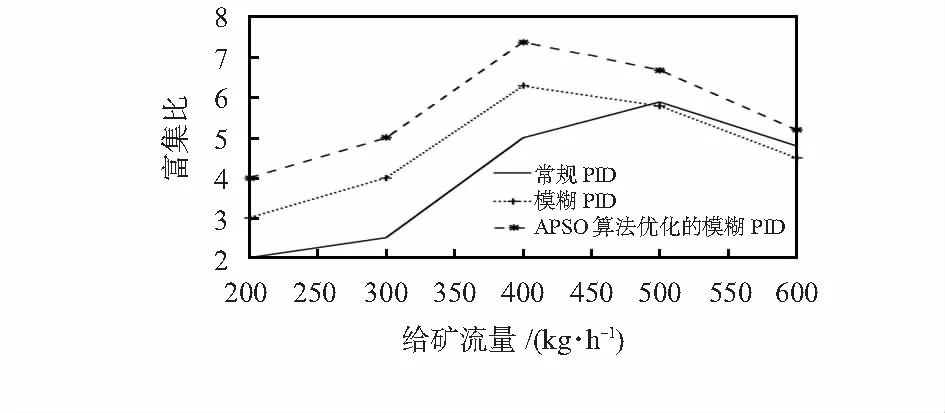
图5 给矿流量响应对比曲线
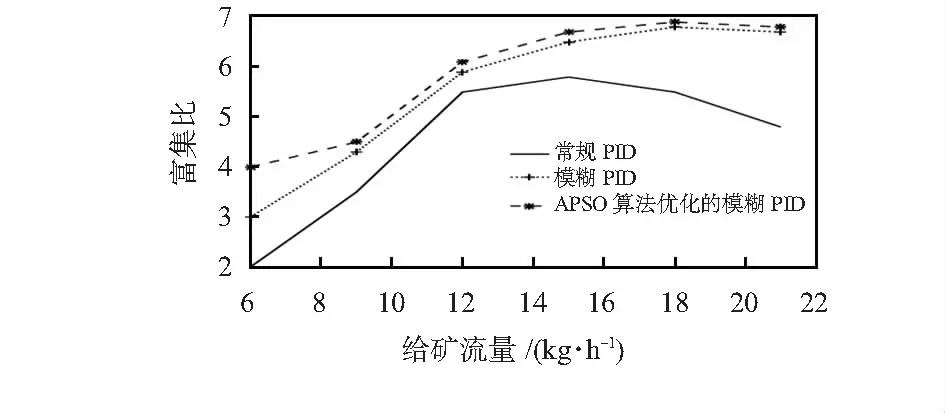
图6 给矿质量分数响应对比曲线
由图5和图6可知,采用APSO算法优化模糊 PID控制器的Knelson离心选矿机,能够明显提高铁精矿富集比。在给矿流量为400 kg/h时,给矿质量分数为14 %~18 %有最大富集比,即Knelson离心选矿机最适宜的给矿流量为400 kg/h,最适宜的给矿质量分数为14 %~18 %。因此,通过以上对比可知,采用APSO优化的模糊 PID控制器的Knelson离心选矿机具有更好的选矿效果。
5 结 论
1)仿真结果表明,本文所设计的基于APSO算法优化的模糊PID控制器与未优化的模糊PID控制器以及常规PID相比较,在给矿流量以及给矿质量分数的控制上,最大超调量减少了5 %~20 %,调节时间和响应速度也明显加快,说明本文所设计的基于APSO算法优化的模糊PID控制器可较好地改善Knelson离心选矿机地选矿效果。
2)实验结果表明,所设计的基于APSO算法优化的模糊PID控制器的能够使Knelson离心选矿机显著提高铁精矿富集比。同时,得出了Knelson离心选矿机最适宜的给矿流量为400 kg/h,最适宜的给矿质量分数为14 %~18 %,有一定的工程应用价值。
