超声衍射时差法近表面盲区减小算法研究*

程 江， 张 旭， 涂 君， 廖春晖

(湖北省现代制造质量工程重点实验室 湖北工业大学 机械工程学院，湖北 武汉 430068)

0 引 言

缺陷定量是超声检测的重要应用方向，黄焕东等人利用信号处理方法对缺陷进行定量[1]，但由于算法复杂,较难应用到工程实践中。近年来，超声衍射时差(time of flight diffraction，TOFD)法因其操作简单、能对缺陷进行定量，在工业无损检测中得到了广泛应用。但受TOFD检测中直通波的影响，被检测工件的上表面存在一定的盲区[2]，使该方法无法检测出近表面缺陷。

为解决这一问题, 原培人等通过将超声相控阵应用于TOFD检测的方法有效提高了近表面检测能力[3];张涛提出一种基于衍射横波的TOFD检测新方法有效识别埋深2mm的缺陷[4];Chen J等人提出一种自适应的去卷法来检测细小和浅表面缺陷[5];孙旭等人通过自回归(AR)谱外推方法将TOFD检测盲区深度由8.3 mm抑制到2.5 mm以内[6];Yeh F W T等人提出一种替代TOFD的方法,使用的衍射是纵向后壁回波和剪切后壁回波中最相关的信号,有效检测出了近表面缺陷[7];Jin S J 等人提出一种模态转换的方法,有效提高了近表面检测精度[8];汪俊等人提出一种通过RLS自适应滤波算法对TOFD图像进行了处理,有效解决近表面盲区问题[9]。以上方法均在一定程度上提高了近表面缺陷的辨识能力，但也存在直通波抑制不完全、对系统硬件要求高、算法复杂及算法鲁棒性差等问题。

经验模态分解(empirical mode decomposition,EMD)是Huang N E于1998年提出的一种信号时频分析方法[10,11]。

该方法基于信号的局部特征时间尺度，把信号分解为若干个本征模态函数(intrinsic mode function, IMF)之和，这些模态函数可以很好地反映信号在任意时间局部的频率特性[12]。EMD本身是完备的[10],不需要选定基函数，可根据信号本身特性自适应产生模态函数，适合处理非平稳信号[13]。超声TOFD检测中回波信号属于非平稳信号，可以通过EMD提取缺陷信息。Hilbert变换对缺陷信息的提取决定于EMD的质量，由于传统的EMD在进行包络提取过程中无法包含非极值的端点信号在分解过程中使误差累加，导致IMF发散[14]，无法提取缺陷回波信号。

本文对传统经验模态算法进行了改进，提出基于AR模型预测的端点延拓算法。在该算法的基础上进行EMD，并选择合适的模态函数进行信号重组。通过对重组后的信号进行希尔伯特(Hilbert)变换提取缺陷衍射信号。通过仿真研究和实验验证，该方法可较好地提取淹没在直通波信号中的近表面缺陷衍射信号。

1 TOFD检测原理

TOFD依靠超声波与缺陷端部相互作用发出的衍射波来检出缺陷并对缺陷进行定量，检测原理如图1所示。

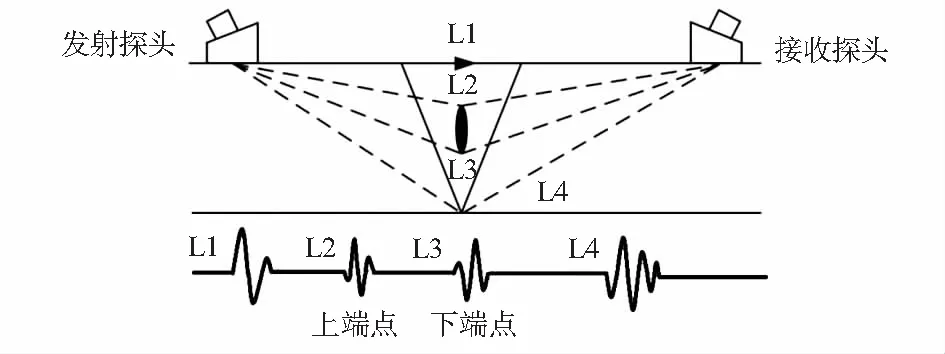
图1 TOFD检测原理

其中，L1为沿工件表面传播的直通波；L2为缺陷上端点衍射波；L3为缺陷下端点衍射波；L4为底面反射波。在薄工件检测或缺陷位于工件的近表面时，由于缺陷衍射波幅度小并受直通波振铃拖尾影响，使L2淹没在L1中无法辨识缺陷衍射信号。

2 EMD和Hilbert变换

2.1 EMD

EMD将信号分解为各个IMF。IMF要满足以下两个条件[15]：1)整个数据范围内，极值点和过零点的数量相等或者相差一个；2)在任意点处，所有极大值点形成的包络线和所有极小值点形成的包络线的平均值为零。

定义x(t)为信号序列,imfn(t)为经EMD得到的固有模态函数,rn(t)为余量,则原始信号可以表示为所有的IMF及余量之和

(1)

设信号序列的上、下包络分别为u(t)和v(t)，上、下包络的平均为m(t),则

m(t)=u(t)+v(t)

(2)

通过筛选，用x(t)减去m(t)后剩余部分h1(t)，即

h1(t)=x(t)-m(t)

(3)

如果h1(t)满足IMF的两个条件，则h1(t)为第一个IMF函数；否则，则用h1(t)代替x(t),设与h1(t)相应的上、下包络线为u1(t)和v1(t)，重复筛选过程直到hk(t)满足IMF条件。

这样就分解得到第一个IMFc1(t)和信号的剩余部分r1(t),即

c1(t)=hk(t)

(4)

r1(t)=x(t)-c1(t)

(5)

对剩余信号部分r1(t)继续进行EMD，直到所得剩余部分为单调信号或其值小于预先给定的值时分解完毕，最终分解得到所有的IMF及余量。因此，原始信号x(t)可以表示为所有的IMF及余量之和

(6)

筛选过程中，由于判断条件苛刻,可能得不到结果,或程序执行时间冗长。习惯上，通过标准偏差(SD)[16]代表筛选条件

(7)

式中h1(k-1)(t)和h1k(t)分别为两个连续的筛选结果。一般来说，SD值越小，所得的IMF分量的线性和稳定性就越好，本文取SD为0.1。

2.2 信号重构与Hilbert变换

根据超声信号的频率及能量分布特点，选择合适的IMF叠加，再进行Hilbert变换。对叠加后的函数进行Hilbert变换后信号可表示为

(8)

式中k为所选IMF总数。经过Hilbert变换可以提取直通波与缺陷衍射波的峰值点，从而区分直通波和缺陷衍射波。

2.3 端点延拓算法

Hilbert变换对缺陷信号的提取质量取决于EMD质量，而由于超声回波信号的端点可能不同时处于极大值或极小值，因此,在利用三次样条函数求解上下包络的过程中,在数据序列的两端会出现发散现象，且该误差随分解的进行而累加，导致无法正确分解原始信号。因此，需要对信号向外进行延拓，以确保包络线包含端点。

超声信号为短时单频信号，而AR模型适合正弦信号的建模。当信号模型合理时，模型产生的数据能够作为真实数据的近似[17]。本文采用基于AR模型的参数估计方法进行端点延拓。AR模型预测的基本原理[18]是：时间序列{y(n)} 中任意时刻的值y(n)可以由其前面L个值的线性组合表示

(9)

式中L为预测模型的阶数，pi为预测系数。建立AR预测模型分两步：1)确定模型的阶；2)求出预测系数pi。对于pi的求取包括直接估计法和递推估计法。本文选择基于最小二乘法的直接估计法进行端点预测。AR模型是全极点的模型，其差分表达式为

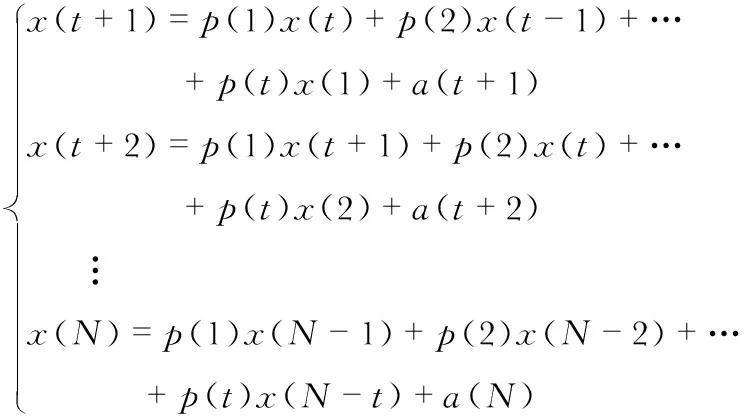
(10)

其矩阵形式为

y=xp+a

(11)

根据多元回归理论，参数矩阵的最小二乘估计为

(12)

则时间序列延拓q步的最佳预测为

(13)

由此可得AR(n)的最佳预测为

(14)

本文选择n=3,q=2进行端点延拓，即对波形的左右两端分别延拓两个极大值点和极小值点。

3 仿 真

采用信号s1(t)和s2(t)并叠加噪声作为接收换能器接收到的信号，如图2所示。其中,s1(t)为直通波信号，s2(t)为缺陷衍射波信号,s(t)为二者叠加后的信号。x(t)为加入随机白噪声后的换能器接收端信号，其中,x(t)信噪比设为15 dB。由图2可以看出，无法从信号x(t)中分辨出s1(t)和s2(t)。

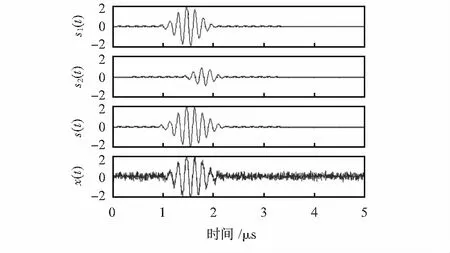
图2 仿真信号

图3为经过AR模型端点延拓算法的EMD结果。可以看出噪声能量多集中在第一、二级IMF中，而最后几级多为低频分量，有用的超声回波信号多集中在中间几级。

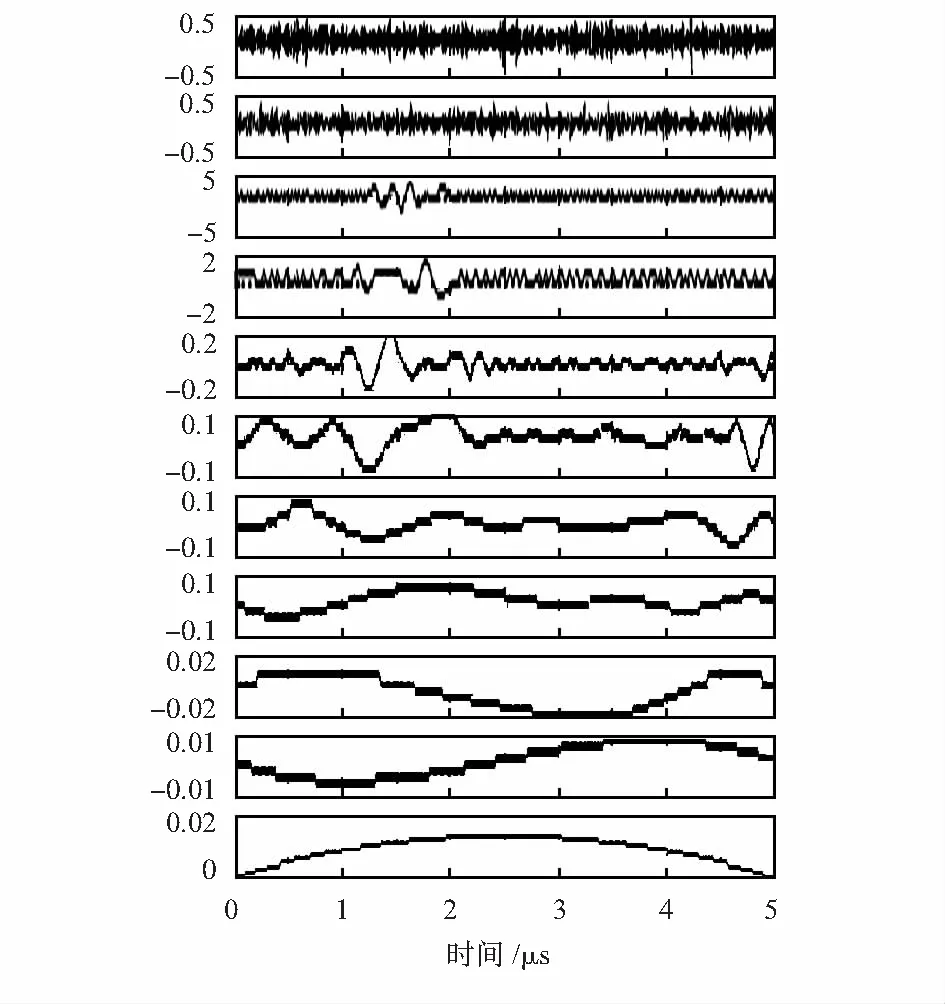
图3 采用极值延拓算法的EMD处理结果

选择合适的IMF进行叠加，再进行Hilbert变换，即可从混合信号中分辨出s1(t)和s2(t)，如图4所示。图4(a)为IMF4～IMF7叠加的结果x1(t)；图4(c)为对x1(t)进行Hilbert变换的结果；图4(b) 为IMF3、IMF4叠加的结果x2(t)；图4(d)为对x2(t)进行Hilbert变换的结果。由图4可以看出，选择不同的IMF对是否能够准确提取缺陷衍射信号起至关重要的作用。根据TOFD检测回波信号的频率和能量分布，一般选取IMF4～IMF7重构信号，因为前面IMF多为高频噪声分量，后面IMF则多为低频趋势项以及换能器产生的低频模态。

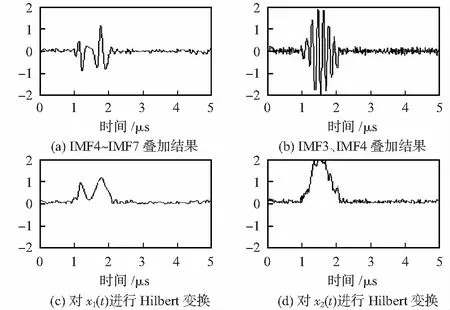
图4 不同模式叠加及进行Hilbert变换结果

4 实 验

利用TOFD—40盲区标准试块进行了实验验证。试块的4个侧面共有8个Φ2 mm的长横孔，缺陷顶端距检测面的埋藏深度3～10 mm,间隔为1 mm。

实验中,采用Panametrics5800超声分析仪进行超声信号的发射与接收放大，采用Tektronix DPO4032示波器进行回波信号采集。采用Panametrics 5 MHz TOFD探头和RT3/6—60LLM纵波楔块，调整到最佳PCS进行扫描检测，如图5所示。

图5 机械扫查示意

分别对8个长横孔缺陷进行了数据采集和算法处理。给出PCS为21 mm时各埋藏深度缺陷衍射重构信号并进行Hilbert变换后的结果，如图6所示，其中a～h分别代表埋藏深度10～3 mm缺陷衍射信号提取结果，紫线表示进行计算选择的有效数据闸门。

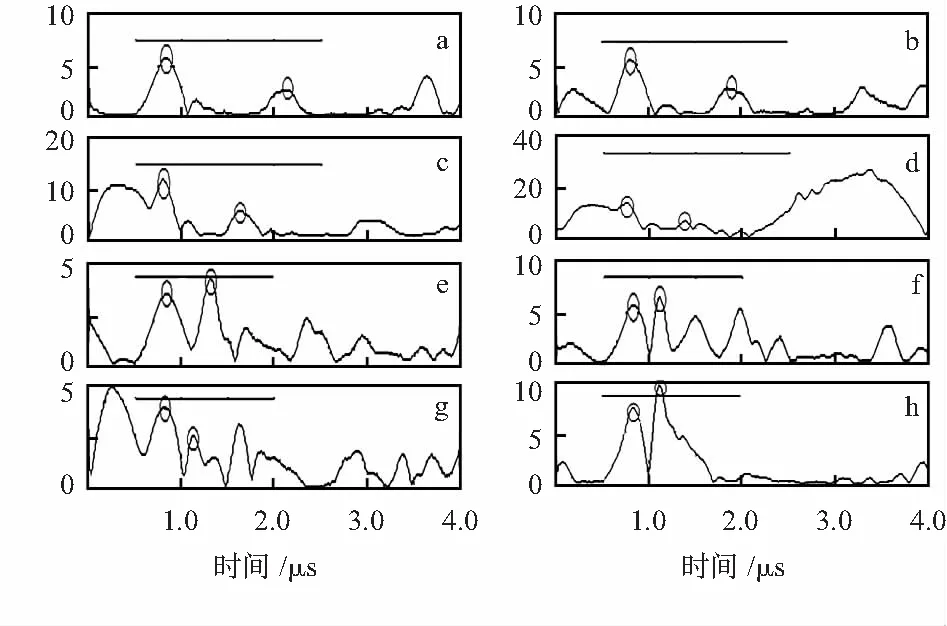
图6 缺陷信号提取结果

由图6可以看出，由于长横孔孔径相对于声波波长太大、孔自身高度太小、孔与工件表面距离太小,因此,在回波信号中会混叠反射、绕射和模式转换的波形，且孔距离表面越近，该现象越明显。由此表明，长横孔并不是理想的TOFD实验试块。但由于裂纹缺陷或闭合裂纹机械上无法加工，因此,可制作开口型尖端试块,或采用电火花等加工方式,尽可能减小长横孔孔径、增加孔高度，以达到仿真裂纹类缺陷的效果。本文在实验过程中，选取适当的测量闸门也可减小其它模式的波对TOFD缺陷回波信号的影响，从混叠的回波中分辨出缺陷回波信号。

对所有8个人工缺陷测试后，进行缺陷深度计算。当使用直通波与缺陷衍射回波的峰值时间差计算缺陷深度时，可以不必考虑楔块延时，根据以下公式计算缺陷深度

(15)

(16)

式中 Δt为直通波与缺陷衍射波传播时间差，c为介质声速，dPCS为探头中心距。

测量结果如表1所示。

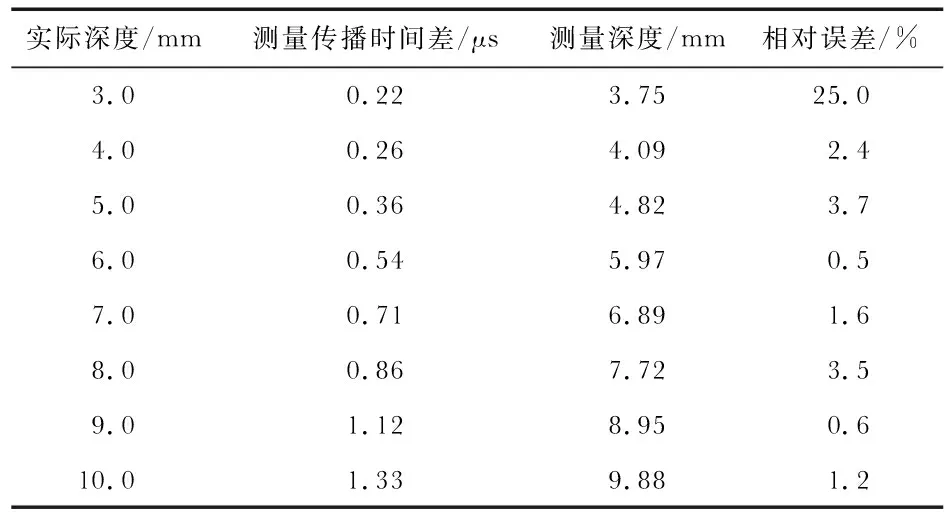
表1 缺陷测量对比

由检测数据可以看出，该方法在检测埋藏深度为3 mm以上的缺陷时具有较好的辨识率，测量相对误差小于3.7 %；当缺陷深度小于或等于3 mm时，仍可以区分直通波和缺陷衍射波，但识别误差较大。

5 结 论

针对超声衍射时差技术近表面盲区问题，提出利用改进的EMD。针对传统经验模态分解过程中端点发散问题,提出利用基于AR模型预测的方法对包络极值点进行延拓。采用改进的算法将超声回波信号分解后，根据各IMF能量和频率分布特点，选择合适的IMF进行信号重构，再进行Hilbert变换,可以较好地从接收信号中识别出近表面缺陷的衍射信号。通过仿真和实验验证，该方法可将TOFD检测盲区降低至4 mm，并具有较高的定位精度；该方法目前仅选择固定IMF模式进行信号重构，未来可研究自适应IMF选择及叠加方法，以增加算法的有效性。