地埋管地源热泵水泥基回填材料导热系数预测模型
2022-06-28董世豪胡自远周超辉周亮宇林德荣
董世豪,胡自远,周超辉,周亮宇,林德荣,倪 龙
(1.哈尔滨工业大学 建筑学院 寒地城乡人居环境科学与技术工业和信息化部重点实验室,哈尔滨 150090;2.山东省地质矿产勘查开发局 第七地质大队,山东临沂 276006;3.中能建地热有限公司,北京 100022)
0 引言
水泥基材料广泛应用于建筑、固井材料、回填材料、岩层封堵、注浆工程等,与人民生活、社会发展息息相关。水泥基材料通常由水泥、骨料(一般为砂或石)及其他改善性能的材料组合而成,其导热系数在很多研究和工程中都是重要参数:在建筑行业,混凝土围护结构的导热系数直接影响建筑能耗;对于地源热泵,地埋管周围的钻孔间隙需用回填材料填实,其导热系数直接影响换热效果。
地埋管地源热泵回填材料有水泥基和膨润土基两种,在基岩地区宜选用水泥基材料,同时水泥基材料也具有更高的导热性能[1]。高导热性能的回填材料对系统节能和减少投资至关重要,ALLAN等[2]研究发现,采用高导热系数的材料可以使地埋管设计长度减少22%~37%;陈卫翠等[3]对通过工程实例计算得出高性能回填材料能够减少地埋管长度29%~36%;BURKHARD等[4]也通过热响应试验发现,采用强化换热材料的钻井热阻可降低27%。因此,针对此类材料的导热性能进行理论研究与建模,可以为高性能材料的开发提供理论指导,对行业发展意义重大。
现有针对水泥基回填材料的研究多局限于试验研究,国内外学者研究发现,水灰比降低[1],砂灰比增大[5-6],添加石墨[5,7]都会使导热系数增加;邹玲等[8]还测定了材料的孔隙率,发现材料孔隙率随水灰比增加而变大。对于导热系数理论研究,有学者针对缓冲材料[9]、岩土[10-12]、建材[13]、食物[14-15]、陶瓷等材料建立了导热模型,但是,适合于水泥基材料的导热模型较少,专门用于水泥基回填材料的导热模型更少,且现有模型直接用于回填材料导热系数预测的误差较大。因此,为了给水泥基材料研究提供一种可应用的导热系数计算模型或方法,本文根据材料的物理结构和组成,结合傅里叶导热定律,建立了水泥基材料导热系数预测模型,基于水泥基回填材料进行了参数识别,并与试验值进行了对比验证。
1 导热系数预测模型的建立
一般水泥基材料由骨料、水泥和水按比例混合而成,成型的材料中存在孔隙,孔隙内含有水分或空气。因此水泥基材料也是一种固-液-气三相混合物,该模型首先针对由骨料和水泥胶结物组成的固相部分建模,然后针对固相(水泥+骨料)、液相(水)、气相(空气)三者的混合物建模。
1.1 固相(水泥+骨料)模型
1.1.1 模型结构
首先针对由骨料和水泥组成的固相建模,该模型可以反映骨料含量对导热系数的影响。进行如下假设:(1)将骨料颗粒将简化为等大的球体;(2)利用球体的重叠反映骨料之间的面接触;(3)材料内部为纯导热。
图1示出固相模型的中央截面。骨料为相互重叠的球体,骨料平均半径为r,角度控制其重叠程度;骨料周围包裹水泥基质,形成半径为(ξ≥1)的圆柱体,通过骨料含量计算出参数。热流方向为从上到下,如图2所示。
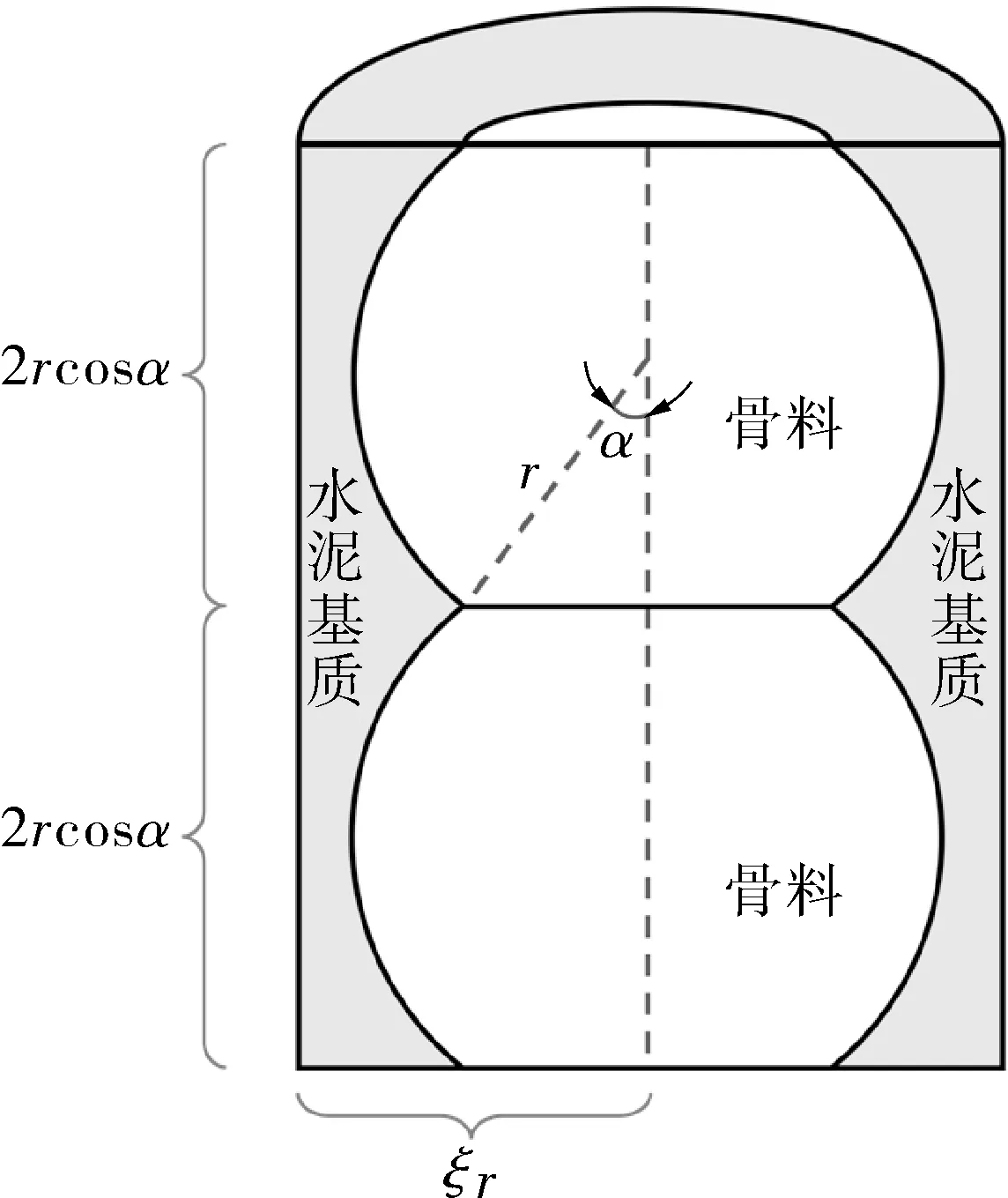
图1 固相导热模型Fig.1 Solid-phase thermal conductivity model
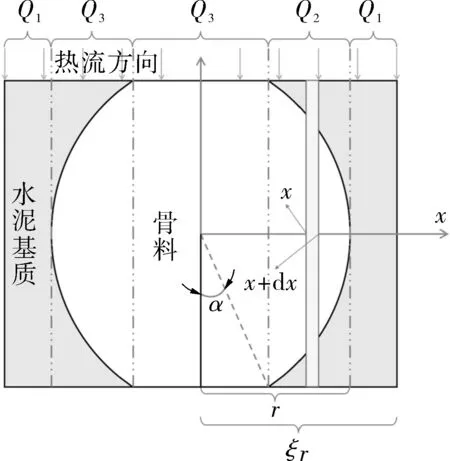
图2 计算单元示意Fig.2 Schematic diagram of calculation unit
1.1.2 模型推导
由图1所示的模型物理结构可计算得到骨料体积分数表达式:
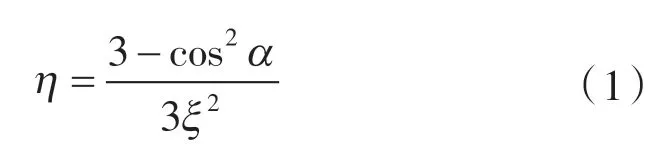
式中 η ——骨料在固相中的体积分数;
α ——衡量骨料面接触程度的参数;
ξ ——与骨料含量有关的参数,ξ≥1。
而骨料体积分数和骨料/水泥质量比的关系为:
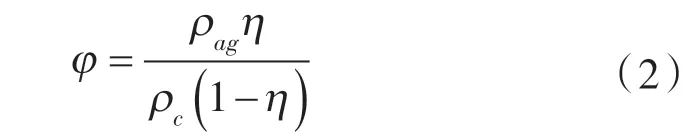
式中φ——骨料与水泥质量比,0≤φ≤1;
ρag——骨料的密度,kg/m3;
ρc——无孔水泥密度,kg/m3。
如图2,取一个骨料颗粒及其周围水泥为计算单元,并建立柱坐标系。设该单元上、下面的温差为ΔT,按几何特征将该单元的热流分为3部分,即图中的Q1,Q2和Q3。第1部分Q1为纯水泥的圆周,其中x∈(r,ξr),根据傅里叶导热定律计算该部分的热流量为:

式中 Q1——第1部分的热流量,W;
λc——水泥基质导热系数,W/(m·K);
r ——骨料颗粒的半径,m。
第2部分Q2包括水泥和骨料,其中x∈(rsinα,r),如图2所示,取dx微元厚度的圆周,则在x处该微元的热阻是:

式中λag——骨料的导热系数,W/(m·K);
R(x) ——x处该微元的热阻,K/W。
则该部分的热流量为:

式中 Q2——第2部分的热流量,W。
式(5)可以进一步计算得到:

第3部分Q3为纯骨料组成的圆柱,其中x∈(0,rsinα),该部分的热流量为:
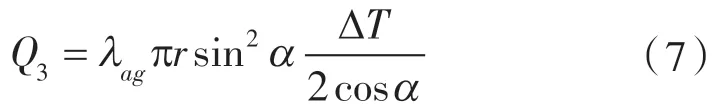
该模型总的热流量为:

将式(3)(6)和(7)代入式(8)中,可以得到与r,ΔT无关的式(9),也即固相模型的有效导热系数λs为:
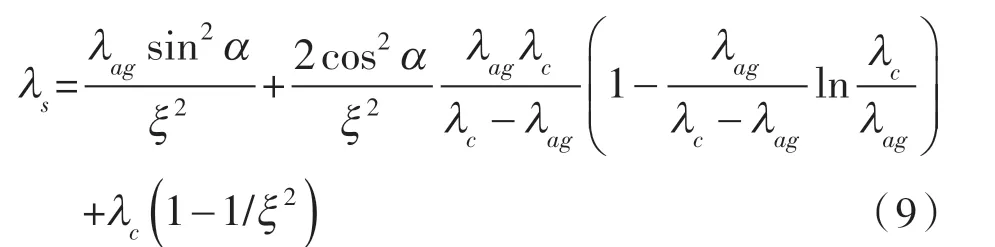
1.2 固-液-气三相模型
1.2.1 模型结构
针对固-液-气三相进行建模,该模型可以反映孔隙率和饱和度对导热系数的影响。一般情况下孔隙率越高导热系数越低。严辰成等[16]通过X射线扫描水泥砂浆的孔隙结构得出,水泥浆体中的孔可以分为气孔和毛细孔,气孔尺寸较大,形状接近球形,毛细孔尺寸较小且形态不规则,难以建立实际结构的模型。现有的导热系数理论计算研究[17-20]也多将孔隙简化为规则形状,从现有研究以及本文研究结果来看,采用这种简化方法得到计算结果的精度能满足工程需要,一定程度上说明了这种方法的可行性。
假设条件如下:(1)材料中的孔隙为椭球体;(2)水分均匀附着在椭球体孔隙周围,且厚度一致;(3)材料内部只存在热传导。
模型如图3和4所示,热流方向为立面图中的从上到下,中间为椭球体孔隙,水分均匀附着在椭球体内壁面。椭球体孔隙(包括液相和气相)长轴为2a,短轴为2βa,通过β控制椭球体短轴从而改变孔隙形状或大小;不包括水分的椭球体(气相)长轴为2κa,短轴为2κβa,通过κ来反映饱和度(0≤κ≤1);孔隙周围是固相材料,模型整体为立方体,底面是边长为2γa的正方形,高为2μa,其中μ≥1,γ≥β。

图3 固-液-气三相模型平面Fig.3 Plan of solid-liquid-gas three-phase model
该模型有3种参数取值方式:
(1)找到γ,μ和a最优值,由孔隙率计算出β;
(2)找到β,μ和a最优值,由孔隙率计算出γ;
(3)找到γ,β和a最优值,由孔隙率计算出μ。
1.2.2 模型推导
根据几何关系得到孔隙率和各参数的关系:

式中 ε —— 孔隙率,定义为块状材料中孔隙体积与总体积的百分比。
β ——几何参数,椭球形孔隙的短轴为βa;
γ —— 几何参数,模型底面边长2γa,且γ≥β;
μ —— 几何参数,模型长方体的高为2μa,且μ≥1;
饱和度和参数κ的关系:

式中 ω —— 饱和度,定义为材料中水的体积与孔隙体积的百分比;
κ ——与饱和度有关的参数,0≤κ≤1。
将该模型作为计算单元,建立如图4所示的柱坐标系,设上下面的温差为ΔT,按几何特征将热流分为3部分,Q1'部分为纯固相部分的圆周,其中x∈[βa,γa];Q2'部分包括液相和固相,x∈[κβa,γa];Q3'部分为包括液相、气相和固相的圆柱,x∈[0,κβa]。按照与固相模型相似的方法得到式(12),即该模型的有效导热系数为:

图4 固-液-气三相模型立面Fig.4 Elevation of solid-liquid-gas three-phase model


式中λe—— 模型有效导热系数,即回填材料导热系数预测值,W/(m·K);
λw——液相导热系数,W/(m·K);
λs—— 固相导热系数,由式(9)得到,W/(m·K)。
λa——气相导热系数,W/(m·K);
式(12)继续推导可得到与a无关的式(13):

2 模型参数识别
该模型中的参数γ,μ和β与材料的几何性质有关,直接测量非常困难,对具体材料,可通过参数识别确定。对于水泥基回填材料,骨料为石英砂,孔隙内为空气(气相)和水分(液相)。本文选取两组独立的实验数据,一组用于参数识别,一组用于模型验证。
2.1 参数识别试验数据与参数取值选择标准
KIM等[21]测量了水灰比为0.7、非饱和状态、不同砂灰比(骨料/水泥质量比)下水泥基回填材料的孔隙率和导热系数,试验值见表1[21],数据均为在室温下测得,而模型中单相材料导热系数也取25 ℃对应的值,因此模型参数取值条件与实验条件基本匹配,可用于参数识别。

表1 参数识别试验数据Tab.1 Experimental data for parameter identification
不同参数取值影响预测值的大小,进而与预测精度有关。首先,使用模型计算表1数据对应的孔隙率、饱和度和砂灰比下的预测值;然后,将预测值与实验值对比得到其相对误差,取这5个预测值的平均误差作为判断标准。参数取值不同可以得到的平均误差也不同,改变参数取值找到平均误差较小或满足精度要求的取值,则模型参数γ,μ和β即可确定。
2.2 单相材料参数取值
回填材料各种单相成分的物性参数见表2。其中,无孔水泥为不包含孔隙的固结水泥。水和空气的导热系数随温度变化,回填材料的工作温度也随工况变化,根据文献[22]给出的地埋管钻孔在取热和排热工况下地层温度分布可知,大部分回填材料的实际运行温度在10~40 ℃范围内。将水在10 ℃和40 ℃时的导热系数代入模型(砂灰比=2,孔隙率=0.22,饱和状态),得到导热系数预测值分别为2.50和2.59 W/(m·K),相差3.47%;同样,将空气在10 ℃和40 ℃时的导热系数代入模型(砂灰比=2,孔隙率=0.22,饱和度=0.3),得到空气的导热系数变化对预测值的影响为0.42%,因此虽然水和空气的导热系数都会受温度的影响,但是其对最终结果影响很小,因此取平均温度25 ℃下的固定值即可。

表2 单相材料物性参数Tab.2 Physical parameters of single phase material
2.3 最佳孔隙率控制方式确定
第1.2.2节提到,模型有3种取值方法,因此需要确定适合于回填材料的最优方法。将不同参数取值方式下的预测值与表1试验值对比,用平均误差作为评价标准。
图5示出了方式(1)不同γ,μ下的平均误差,γ一定时,μ越大,误差越小,当μ增加至1.4时,误差约17%,但是可预测的最大孔隙率仅37.40%,可预测孔隙率范围过小。图6示出了方式(2)不同μ,β下的平均误差,平均误差几乎不随β变化;而β一定时,平均误差随μ增大而减小,当达到1.4时,其平均预测误差减小至15.65%,但其可预测的孔隙率范围仍然过小。因此,方式(1)、(2)误差均较大。

图5 不同γ,μ 取值下的平均误差Fig.5 Average error under different values of γ and μ
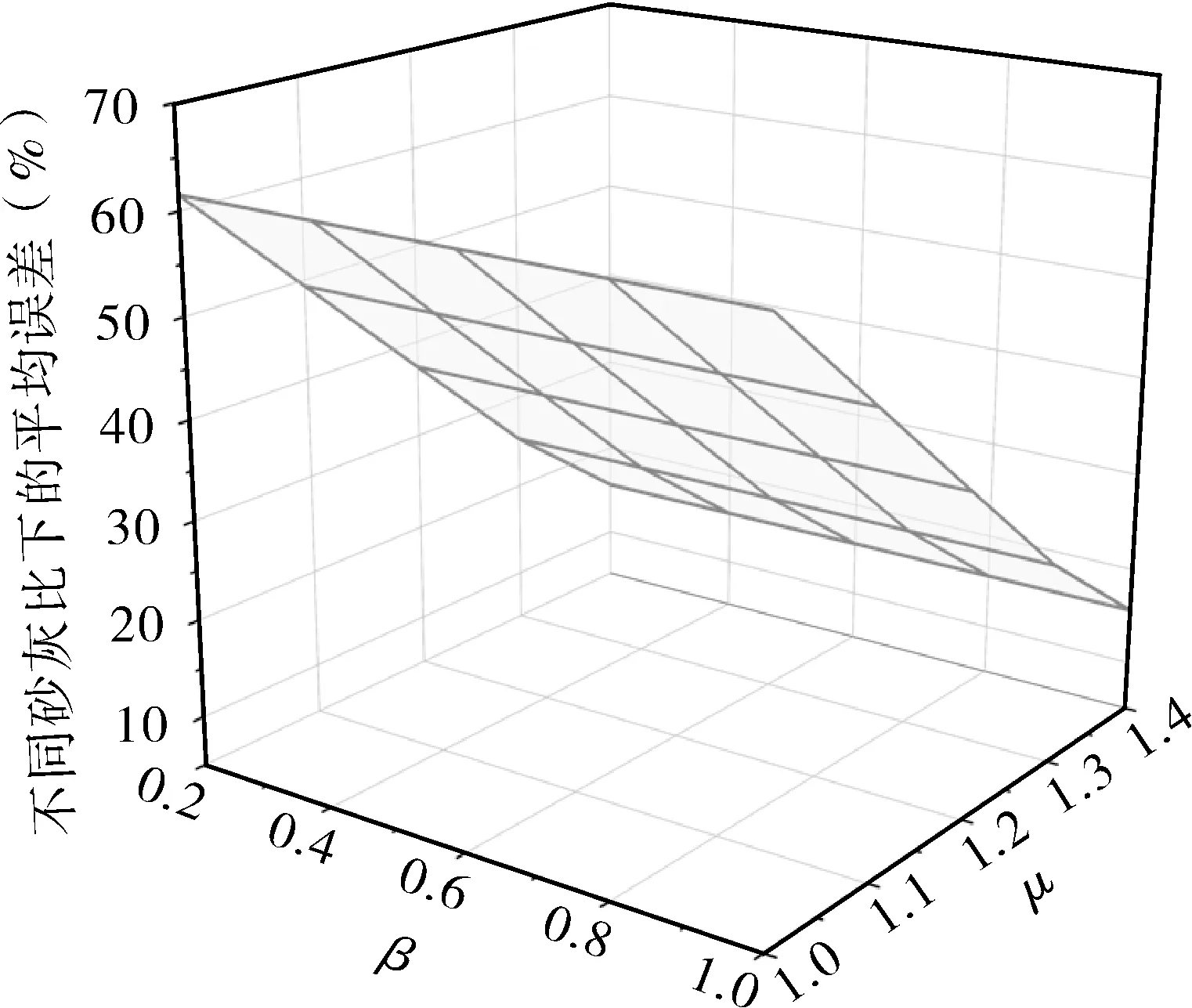
图6 不同μ,β 取值下的平均误差Fig.6 Average error under different μ and β
图7 示出了方式(2)在不同β,γ值下的平均误差,当β略小于γ时,平均误差低于10%,当β=0.95,γ=1.00时,平均误差低至4.36%,可预测的最大孔隙率为0.472 5。综上,参数取值方式(2)更适合于水泥基回填材料。

图7 不同γ,β 值下的平均误差Fig.7 Average error under different values of γ and β
2.4 参数γ,β的识别
以表1试验数据为基准,进行试算。图8示出了γ,β不同取值对预测误差的影响,误差随参数β(γ≥β)的增加,先降低后增加,且在γ取值不同时变化趋势一致,但是取得最小值的位置不同,γ越小,曲线整体向左移;当γ=1.00,β=0.96时,平均误差为3.67%,在各取值组合中最小。
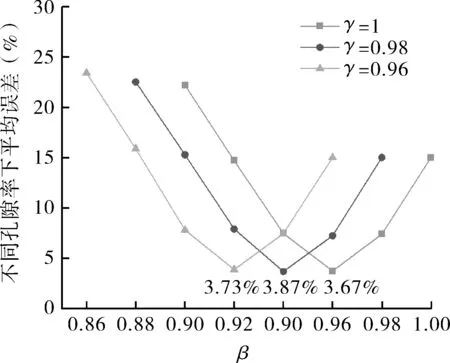
图8 不同β,γ值下,预测误差随孔隙率的变化Fig.8 The variation of prediction error with porosity under different β and γ
2.5 参数识别结果
适用于水泥基回填材料的最佳参数取值方式为:找到γ和β最优值(β=0.96,γ=1.00),通过试验得到的孔隙率计算出μ值。模型识别误差如图9所示,预测值与试验值非常接近,且变化趋势一致,误差在1.49%~6.80%之间,说明参数识别结果较为精准。

图9 参数识别误差Fig.9 Parameter identification error
3 模型验证及比较
3.1 模型验证试验数据
邹玲等[8]测试了水泥基回填材料在砂灰比为2、饱和状态时,水灰比和孔隙率对导热系数的影响;KIM等[21]还测量了在水灰比为0.7、饱和状态时,不同砂灰比下回填材料的孔隙率和导热系数。
邹玲等[8]还指出,砂灰比大于2.2会使材料的流动度过低,影响实际应用;文献[6]提出,水灰比太小会导致流动度太差,过大会导致导热性能变差,水灰比0.45~0.70为宜;对于地源热泵,回填材料与岩土导热系数之比在1~1.2左右较优[28],过高则会导致地埋管之间的热短路,因此回填材料导热系数一般不超过3 W/(m·K);同时,由于地下水存在,回填材料的工作状态多为饱和状态。因此表3数据可以涵盖回填材料研究和工程应用的常见配比范围。

表3 模型验证试验数据Tab.3 Experimental data for model verification
3.2 模型验证
将最优参数取值代入模型,计算饱和状态不同孔隙率下的导热系数,并与邹玲等[8]的试验数据对比,对比结果如图10所示。预测值与试验值变化趋势一致;预测值整体略高于试验值,在孔隙率为0.163时误差低至1.49%,最大误差也仅为5.94%,总体上预测较精准。

图10 饱和状态不同孔隙率下的预测结果Fig.10 Prediction results at different porosity in saturated state
对于饱和状态,图11示出了预测值与表3中KIM等[21]试验值的对比结果,预测值与试验值变化趋势一致,均随砂灰比增加而增加,但是预测值普遍低于试验值,预测误差在3.98%~15.26%之间。但只有砂灰比在2.5及以上时误差超过12%,而此时过高的砂灰比已经使流动性降低而影响实际应用了。因此,总体上预测较精准,满足实际工程与研究需要。

图11 饱和状态不同砂灰比下的预测结果Fig.11 Prediction results under different sand-cement ratios in saturated state
3.3 误差分析
误差来源于实验误差和模型误差。对于实验误差,不同文献采用的材料品质、制作工艺不同可能造成同样配比材料的导热系数差异,另外,孔隙率、导热系数等参数测量过程本身也存在误差。对于模型误差,实际的骨料(石英砂)颗粒并不会像模型中那样形状规则,而且孔隙之间存在联通;同时,本模型未考虑对流换热,但实际的孔隙内的空气或水会存在热对流;含水量较高时也会存在热湿迁移现象,所以饱和状态的试验值通常会偏大,也就导致了图11中饱和状态预测值普遍偏小。
3.4 模型比较
本文还应用现有经典模型进行了导热系数计算,并将其预测精度与本文模型进行了比较。
3.4.1 经典模型
(1)Bruggeman模型。
Bruggeman模型[29]基于平均场理论,假设分散相在连续相介质中随机分布,通过微分再积分方法建立了二元复合材料等效导热系数计算模型:

式中 f ——分散相的体积分数;
kd——分散相的导热系数,W/(m·K);
ke—— 复合材料的有效导热系数,W/(m·K);
kc——连续介质导热系数,W/(m·K)。
该模型可直接应用于二元复合材料,而水泥基回填材料属于多相材料,因此可通过重复应用该模型来得到其导热系数。
(2)Maxwell模型。
假设分散相为球型颗粒且随机分布,且分散相颗粒温度不影响邻近分散相颗粒的温度分布,通过求解分散相颗粒随机均匀地分布在连续相中的导热问题获得了Maxwell模型[30]:
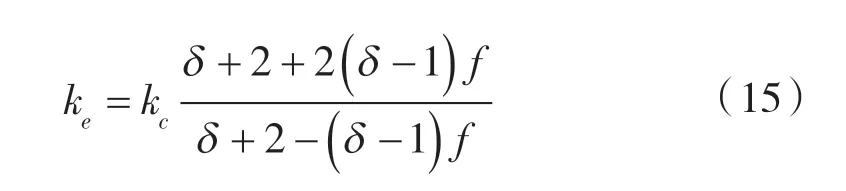
式中 ke—— 复合材料的有效导热系数,W/(m·K);
kc——连续介质导热系数,W/(m·K);
δ ——分散相与连续相导热系数之比;
f ——分散相的体积分数。
3.4.2 本文模型的优势
图12示出了采用本文模型、Bruggeman模型[29]和Maxwell模型[30]计算得到的误差。经过比较,本文模型相对于现有模型的优势如下。

图12 采用不同模型计算的误差Fig.12 Errors calculated by different models
(1)精度更高:本文模型的预测误差均在1.49%~15.26%之间,预测精度较高;而应用经典模型得到的预测误差较大,Maxwell模型的预测误差多个点超过20%误差线,Bruggeman模型误差甚至超过了80%。
(2)可预测的物质组成更复杂:本文模型可以直接预测由骨料、水泥、水和空气4类物质,3种相态组成的复合物的导热系数,现阶段可以做到准确预测这类复合物质导热系数的模型较少;而经典模型大多针对二或三元复合材料进行建模。
(3)可预测影响参数更多:本文模型可以同时预测单相材料导热系数、孔隙率、骨料含量、饱和度等多种参数对导热系数的影响,而现有模型多针对简单物质建模,能够做到同时预测多种参数对导热系数影响的模型较少。
(4)模型物理结构更严谨:经典模型一般未考虑颗粒接触与孔隙的几何形态,因而对水泥基材料的适用性较差,这都导致了预测误差较大;本模型充分考虑了骨料含量较大时可能出现的面接触现象,使物理结构更贴近实际。
(5)灵活性更高:不同用途水泥基材料具有类似的物理结构,但是其导热系数规律可能有差别。而经典模型参数固定,无法通过参数识别,确定不同用途水泥基材料的最优参数,灵活性不及本文模型。
4 结论
本文建立水泥基材料的导热系统预测模型,并进行了参数识别和模型验证,得到了适用于地埋管地源热泵回填材料的参数取值。主要结论如下:
(1)找到参数β,γ最优值,通过孔隙率计算得到μ,可以得到较好的预测精度,β=0.96和γ=1.00为适用于地埋管地源热泵回填材料的最优参数取值;
(2)该模型可以精准预测不同孔隙率下的导热系数,预测误差在1.49%~5.94%之间,也能较精准预测不同砂灰比(骨料含量)、不同饱和度下的导热系数,预测误差在1.49%~15.26%之间;
(3)本文模型预测精度优于传统的导热系数预测模型,本文模型误差最大为15.26%,Maxwell模型的预测误差多个点超过20%,Bruggeman模型误差更大,甚至超过了80%;且具有可预测参数多、可预测物质组成复杂、物理结构严谨、灵活性高等优势。
