基于因子设计法优化和预测水下不分散混凝土的抗分散性能

2022-06-28孙国文张国强王彩辉王亚倩

建筑材料学报 2022年5期

张营，孙国文，2，张国强，王彩辉，2，王亚倩

（1.石家庄铁道大学材料科学与工程学院，河北石家庄 050043；2.河北省交通工程与环境协同发展新材料重点实验室，河北石家庄 050043；3.石家庄铁道大学四方学院基础部，河北石家庄 051132）

水下不分散混凝土的絮凝性、流动性和水陆强度比是保障水下工程施工质量的关键性能［1］，传统的性能设计方法均为基于经验的强度设计理论，已不能满足复杂水域工况下的施工技术需求.为了确定性能影响因素之间的相互关系，常采用正交设计法进行试验设计，该方法虽可满足一般试验需求，但无法找到各影响因素交互的最佳平衡点，也不能对混凝土性能进行有效预测［2］.研究人员仍在不断探索基于性能需求的新设计方法.Cui 等［3］采用多因素方差分析法确定了调节凝结时间、抗压强度以及抗分散性能的设计方法.Song 等［4］为了提高水下灌浆的抗分散性能，通过单因素法研究了合成抗分散剂的抗分散性能.Jiang 等［5］采用单因素法确定了水下抗分散剂的配比和砂浆中水溶性聚合物的适宜用量.Sonebi等［6‑7］基于遗传规划方法确定了自密实混凝土新拌和硬化性能较好的试验配比.

试验设计是一种安排试验和分析试验数据的数理统计方法［8］.在各试验设计法中，因子设计法不但可以分析各因子间交互作用对试验结果的影响［9］，而且能在给定的约束条件下建立优化的试验方案并进行性能预测［10］，已在新产品开发、工程试验等领域得到应用［11］.对水下施工用的不分散混凝土，因施工周围水域环境多变，如何对其各项性能进行适时调控和预测，是当前迫切需要解决的难题.本文基于因子设计法，对影响水下不分散混凝土性能的水胶比1）文中涉及的水胶比和用量等均为质量比或质量分数.、絮凝剂用量、减水剂用量这3 个关键因子进行设计，并建立扩展度（流动性衡量指标）、悬浊物含量（絮凝性衡量指标）和水陆强度比的数学预测模型，以满足基于性能需求的工程需求.

1 试验

1.1 原材料

胶凝材料采用上海舜安建材有限公司生产的双快硫铝酸盐水泥（C）；絮凝剂采用羟丙基甲基纤维素（AWA），由石家庄市瑞鑫纤维素有限公司生产；减水剂采用自主合成的聚羧酸减水剂（PC）.

1.2 试验方法

参照GB/T 8077—2012《混凝土外加剂匀质性试验方法》进行扩展度（S）测试，以扩展度（S）来表征水下不分散混凝土的流动性.

参照GB/T 37990—2019《水下不分散混凝土絮凝剂技术要求》测试悬浊物含量（W），以此来表征水下不分散混凝土的絮凝性.

参照GB/T 37990—2019《水下不分散混凝土絮凝剂技术要求》，在空气中和水下进行试件的成型和养护；参照GB/T 50081—2019《混凝土物理力学性能试验方法标准》，进行28 d 抗压强度的测试以及水陆强度比（P）的计算.

2 因子设计法对水下不分散混凝土絮凝性的设计与优化

2.1 因子设计法的原理

因子设计法通过分析不同因子的不同水平，来估计单因子作用和多因子之间的相互作用，可分为单因子、全因子和部分因子设计.

克服单因子试验中交互问题的一种方法是：在1 个试验中计算各因子所有可能的组合，这种方法称为全因子设计法.全因子设计法是一种理想的设计，完整的因子设计允许在有或没有交互作用的情况下，对其性能进行建模预测，并且当因子数量增加时，可以快速发现应用程序的限制，可确定因子对响应的影响以及不同因子之间的相互作用［12］.本文考虑到水下不分散混凝土抗分散性影响因素相互交织，因此选用全因子设计法.全因子设计法中每个因子的水平限制为2 个（低和高），一般全因子设计法的因子数量不超过5 个，否则耗时成本太高.

全因子设计法中实际的因子范围需要转换为无量纲编码值ψ，其计算如下［13］：

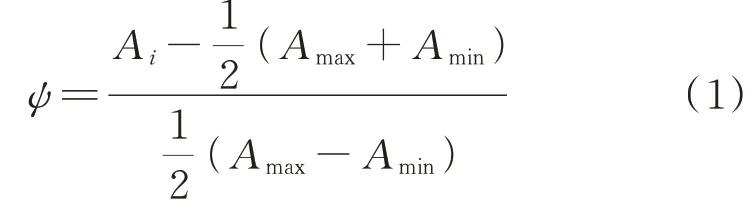
式中：Ai为某个因子；i为该因子按照大小的排序；Amax为该因子的最大值；Amin为该因子的最小值.

2.2 因子设计法在水下不分散混凝土抗分散性能设计中的应用

2.2.1 水下不分散混凝土抗分散性能的因子设计

由文献［14‑15］可知，影响水下不分散混凝土抗分散性能的3 个主要因子是水胶比（mW/mB）、絮凝剂用量（wAWA）和减水剂用量（wPC），其中wAWA和wPC以水泥质量计.设计因子编码与水平如表1 所示，其中全因子设计法每个因子取低（-1）和高（+1）2 个水平，设计时以（0）为中心点，根据式（1）计算因子编码.

表1 设计因子编码与水平Table 1 Coding and level of design factors

根据优化结果选择低、高水平的因子进行试验设计，全因子设计23编码形式的数学模型如下：

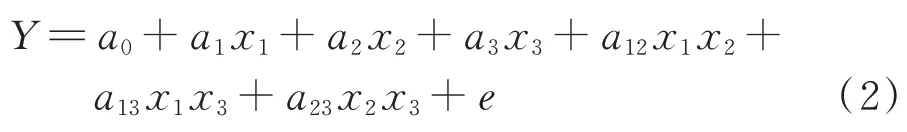
式中：Y为预测值；a0为全局平均值；ai为模型回归系数，即自变量对响应的贡献；x1、x2、x3分别为变量wPC、wAWA、mW/mB；e为不受控制变量影响的随机误差项.

2.2.2 水下不分散混凝土抗分散性能因子设计的模型导出过程

采用全因子设计法，根据表1 建立水下不分散混凝土的流动性（衡量指标为扩展度（S））、絮凝性（衡量指标为悬浊物含量（W））和水陆强度比（P）的统计模型，模拟wAWA、wPC和mW/mB对水下不分散混凝土流动性、絮凝性和水陆强度比的影响，结果如表2所示.

表2 基于因子设计法的试验配比及试验结果Table 2 Mix proportion and test results based on factorial design method

根据表2 中的试验结果，来判断各因子的影响程度及其相互作用，即ai，计算式如下：

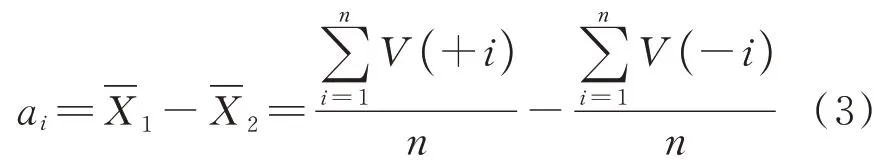
式中：V为试验值为平均值的下标为试验的组数；n为试验次数.

通过假设检验t分布来检验不同模型回归系数ai的影响程度ti，并判断模型的回归系数是否为显著性系数，计算式如下：

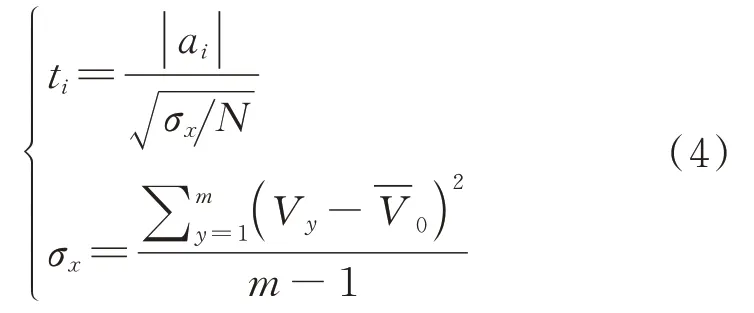
式中：N为阶乘点的试验次数，本文中为23，即N=8；m为中心点的试验次数，m=6；σx为标准差；Vy为y轴中心点的观测值为中心点的平均值.

根据表2和式（2）～（4）得到的方差分析及显著性检验结果如表3～5 所示.由统计学可知，当置信度为95%、自由度（df）为m-1=5 时，查t分布表可知ti=2.57，当ti＜2.57 时，在统计学上对结果的影响可忽略［16］.表3～5 中在假设检验中常用到p值方法（p‑value），其结果均小于0.05，表明wPC、wAWA、mW/mB对水下不分散混凝土流动性、絮凝性和水陆强度比的影响较为显著.需要说明的是，表3～5 中残差（residual）计算的是样本观察值与估计值之差的各项指标；SS 为离差的平方和.

根据因子设计法、表1～5 和式（2）可建立wPC、wAWA、mW/mB对水下不分散混凝土扩展度（S）、悬浊物含量（W）和水陆强度比（P）影响的数学模型：

在表3～5 中，方差分析是通过F检验来判断模型的回归效果，通过分析剔除不显著系数，使得到的模型准确性更高.回归方程的有效性基于Fisher 统计，F值为在显著性和一定数量自由度的水平上，构成F分布.残差平方和的计算式见式（8），F值的计算式见式（9），计算结果列于表3～5.

表3 流动性回归方程的方差分析及显著性检验结果Table 3 Analysis results of variance and significance test for S model

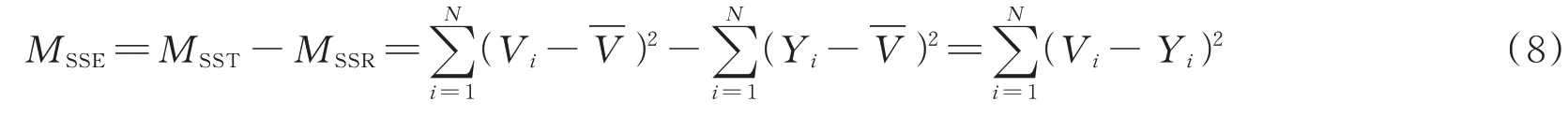
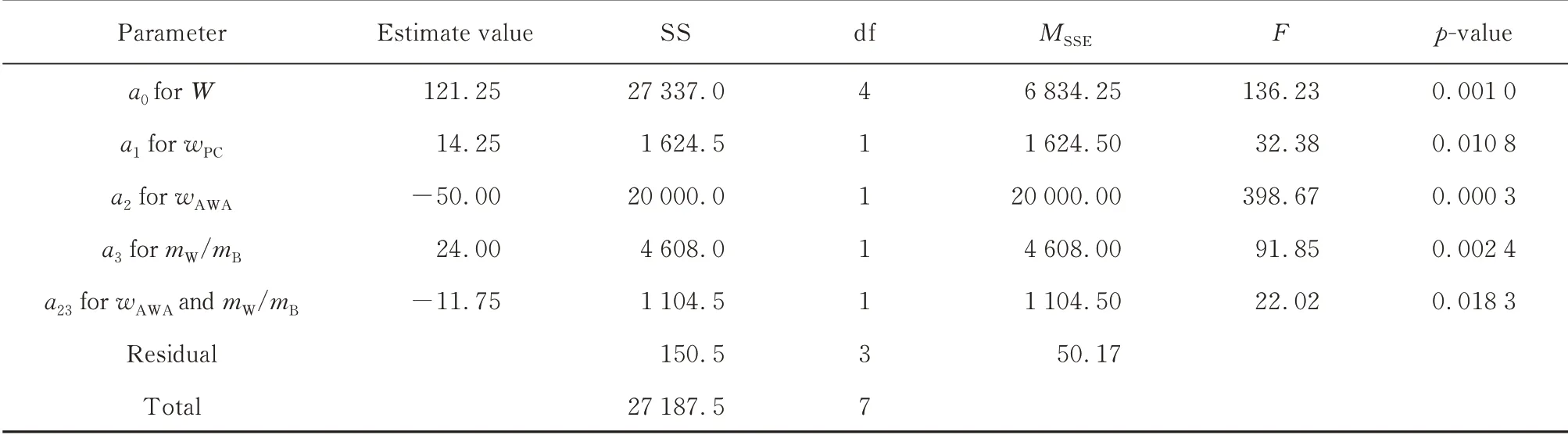
表4 絮凝性回归方程的方差分析及显著性检验结果Table 4 Analysis results of variance and significance test for W model

表5 水陆强度比回归方程的方差分析及显著性检验结果Table 5 Analysis results of variance and significance test for P model

根据式（9）得到在置信度为95%时，F值为19.3.由表3～5 可见，扩展度、悬浊物含量和水陆强度比的F值基本都大于19.3，表明由式（5）～（7）得出的扩展度、悬浊物含量和水陆强度比模型对试验值的预测较为准确.

此外，表3～5 中的负值表示随着wAWA、wPC和mW/mB的增大，扩展度、悬浊物含量和水陆强度比3个模型（式（5）～（7））的预测值降低.在各因子范围内，固定其中1 个因子，采用式（5）～（7）模型可研究其他因子对性能的影响.由表3～5 可知：流动性模型（扩展度）中mW/mB和wAWA对扩展度的估计值分别为88.63 和59.38，絮凝性模型中mW/mB和wAWA对悬浊物含量的估计值分别为24.00 和50.00；当wPC固定时，mW/mB增加对扩展度和悬浊物含量的影响（estimate value）分别是wAWA增加时的1.49、0.48 倍；各因子对水下不分散混凝土扩展度影响大小依次为mW/mB、wPC和wAWA，对悬浊物含量影响大小依次为wAWA、mW/mB、wAWA和mW/mB间的相互作用、wPC，对水陆强度比的影响大小依次为wAWA、wPC和mW/mB.

2.2.3 水下不分散混凝土抗分散性能导出模型的可靠性分析

为了验证统计模型的试验误差，对各因子中心点的配比进行了6 次重复试验.根据表1 计算中心点扩展度、悬浊物含量、水陆强度比的统计结果（平均值、变异系数、相对误差、标准偏差及平方和的预测误差），如表6 所示.由表6 可见，在置信度为95%时，相对误差均在1.50%～3.00%之间，而且反映一个数据集离散程度的标准偏差也较小，表明水下不分散混凝土的扩展度、悬浊物含量和水陆强度比模型（式（5）～（7））的预测值可靠.

表6 流动性、絮凝性、水陆强度比的统计结果Table 6 Statistical results of slump，anti-washout and underwater/in-air strength ratio

相关系数（R2）反映试验值与预测值之间的相关性，R2越接近100%，说明所选择的因子与测试性能的相关性越好.通过计算得到扩展度、悬浊物含量和水陆强度比的相关系数，如表7 所示.由表7 可知，R2均大于90%.需要强调的是本文也应用了调整相关系数（AdjR2）和预测相关系数（PredR2）来进行校验，由表7 可见，两者均超过90%，而且两者较为接近，说明所得回归模型较精确.相反，如果两者都较小，则说明拟合的模型不合理，需要考虑是否有其他对模型影响较大的因素。

表7 流动性、絮凝性和水陆强度比的相关系数Table 7 Correlation coefficient of slump，anti-washout and underwater/in-air strength ratio%

图1 给出了扩展度、悬浊物含量和水陆强度比试验值和预测值的对比.由图1 可知，各性能指标的试验值和预测值均较为相近，说明wAWA、wPC、mW/mB与流动性、絮凝性和水陆强度比的相关性很好，也反映出水下不分散混凝土流动性、絮凝性和水陆强度比的模型预测精确度较高.

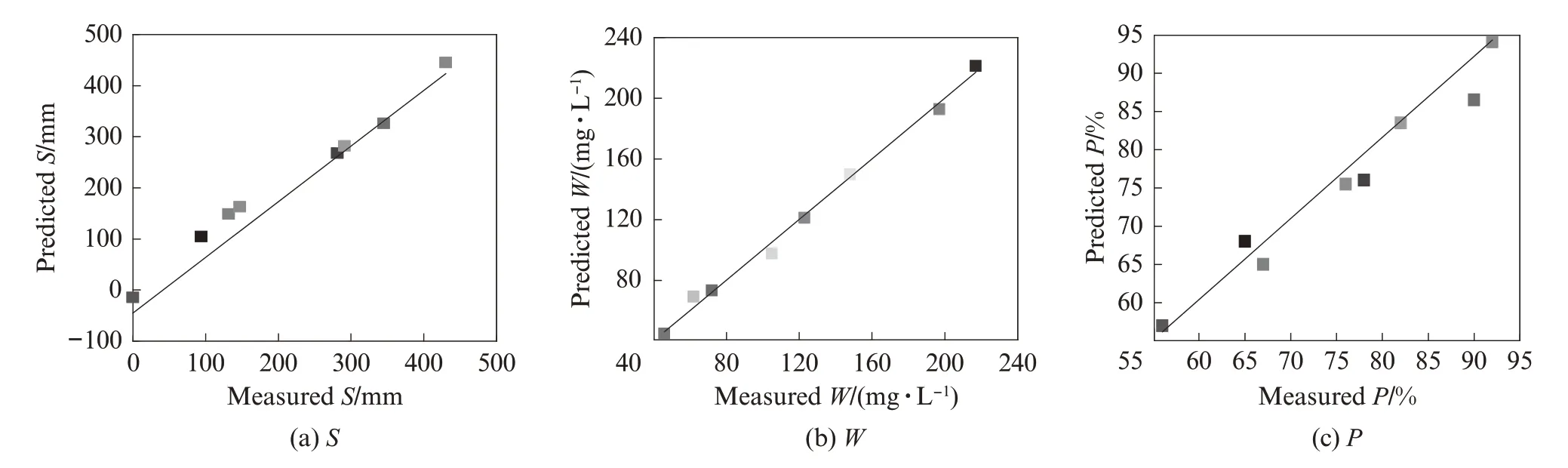
图1 流动性、絮凝性和水陆强度比试验值和预测值的对比Fig.1 Comparison of measured values and model predicted values for slump，anti‑washout and underwater/in‑air strength ratio

3 水下不分散混凝土性能预测

3.1 AWA 和PC 用量对水下不分散混凝土流动性的影响

根据式（5）预测AWA 和PC 用量对流动性的影响，结果如图2 所示.由图2 可知，当wAWA和mW/mB固定时，随着wPC的增加，水下不分散混凝土的流动性增大；当wPC和mW/mB固定时，随着wAWA的增加，水下不分散混凝土的流动性减小；当wPC和wAWA固定时，随着mW/mB的增大，水下不分散混凝土的流动性增大.对于给定的mW/mB，当wPC增加时，可以得到指定流动性的wAWA.这可用于选择外加剂的最佳组合，以达到最大的流动性.

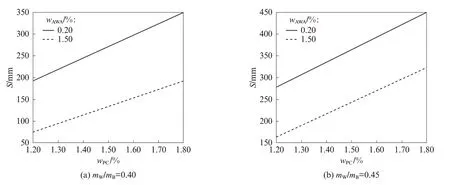
图2 AWA 和PC 用量对流动性的影响Fig.2 Influence of PC and AWA amounts on slump

3.2 mW/mB和AW 用量对水下不分散混凝土絮凝性的影响

根据式（6）预测水灰比和AWA 用量对絮凝性的影响，结果如图3 所示.由图3 可知：当wAWA和wPC固定时，随着mW/mB的增加，水下不分散混凝土的悬浊物含量增大，即絮凝性降低；当wPC和mW/mB固定时，随着wAWA的增加，水下不分散混凝土的悬浊物含量减小，即絮凝性提高；当wAWA和mW/mB固定时，随着wPC的增大，水下不分散混凝土的悬浊物含量增大，即絮凝性降低.对于给定的wPC，当mW/mB增加时，可以得到指定悬浊物含量的wAWA.这可用于选择外加剂的最佳组合，以达到最小的悬浊物含量.

图3 水灰比和AWA 用量对絮凝性的影响Fig.3 Influence of water‑binder ratio and AWA amount on anti‑washout

3.3 AWA 和PC 用量对水下不分散混凝土水陆强度比的影响

根据式（7）预测AWA 和PC 用量对水陆强度比的影响，结果如图4 所示.由图4 可知，当wAWA和mW/mB固定时，随着wPC的增加，水下不分散混凝土的水陆强度比（P%）减小；当wPC和mW/mB固定时，随着wAWA的增加，水下不分散混凝土的水陆强度比增大；当wPC和wAWA固定时，随着mW/mB的增大，水下不分散混凝土的水陆强度比减小.对于给定的mW/mB，当wPC增加时，可以得到指定水陆强度比的wAWA.这可用于选择外加剂的最佳组合，以达到最大的水陆强度比.

图4 AWA 和PC 用量对水陆强度比的影响Fig.4 Influence of PC and AWA amounts on underwater/in‑air strength ratio

通过对流动性、絮凝性和水陆强度比模型的全局优化，得出的最优解为：wPC=1.47%，wAWA=0.86%，mW/mB=0.39.在此条件下预测的S=184.0 mm，W=113.2 mg/L，P=77.4%.选取上述最优解进行试验验证，结果如表8 所示.由表8 可见，预测结果与试验验证结果基本一致，S、W、P的预测精度均在98%以上.