从“一以贯之”到“扩充拓展”——运算意义教学的核心问题再讨论

□董文彬

一、问题的提出：一次观课引发的思考

“长颈鹿与小鸟”是北师大版教材二年级上册第九单元“除法”第一课时的学习内容（如图1）。学生根据数学信息提出了数学问题。教学第一个问题“长颈鹿要准备几间房子”时，学生筛选信息后尝试解答，其中一个学生表达了自己的想法：用除法解决，6个6个地分，每份一样多，是平均分，列式计算是42÷6=7（间）。另一个学生质疑：为什么用除法解决？该学生回应：因为这个问题是平均分，所以是42÷6=7。接着教师让学生根据题目要求“写一写，画一画，用喜欢的方式解释42÷6=7”。随后学生汇报呈现了五种方式：①画圆圈图：画42个圆圈，6个分1组，能分7组，所以42÷6=7（间）；②用减法：42-6-6-6-6-6-6-6=0，减了几个6就是几间房；③画数线图：从42 开始每次减6，减7 次，减到0；④列表；⑤运用乘法口诀：六七四十二，42÷6=7。教师自始至终对于学生的想法“6个6个地分，每份一样多，是平均分，所以用除法解决”没做回应或默认合理。

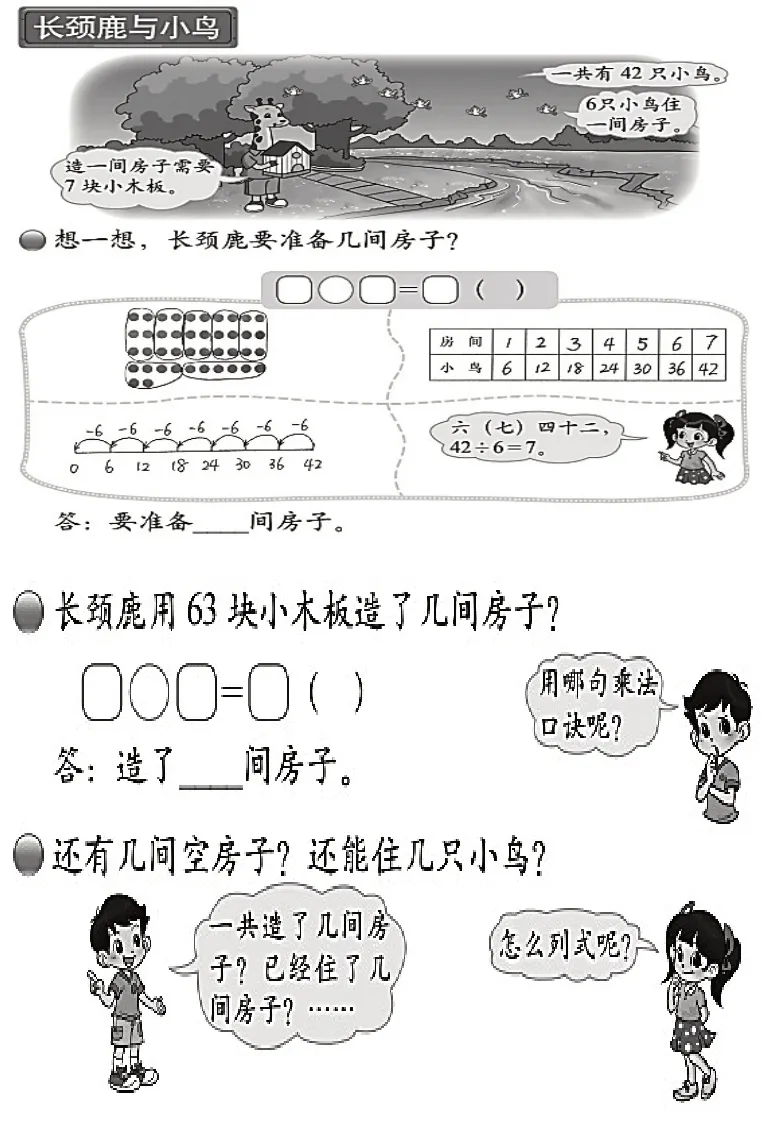
图1

问题引发思考：“已知6只小鸟住一间房子，一共有42 只小鸟，长颈鹿要准备几间房子？”解决这个问题时学生选择用除法，理由是“这是‘平均分’问题”。在小学第一学段，学生对除法概念本质的理解就是“平均分物”。由于前面学习“分一分与除法”单元时，教材呈现的多半是等分情境，这就先入为主地给学生造成了“除法就是将总数平均分给已知人数的等分（分配）过程”的认识。因此，大多数学生简单地将“平均分”等同于“等分”。但此情境中要解决的问题是“等分”吗？此问题用“等分”来解释“为什么用除法解决”合理吗？除法源于“平均分物”，是不是说除法的意义就是“等分”？在这里除法的意义用“等分”还解释得通吗？除法意义的教学情境是否需要扩充和拓展？

二、核心问题再讨论：运算意义是“一以贯之”还是根据学习内容“扩充拓展”

聚焦“案例”体现的问题是：教师试图将“平均分物”模糊地贯穿于不同的问题情境中，来解释除法运算的意义。换言之，上述案例所暴露出的核心问题是：运算意义是“一以贯之”还是根据不同问题情境或学习内容进阶“扩充拓展”？这确实是运算教学中一个值得探讨的核心问题。

（一）追溯除法意义的认识

1.从“平均分”说起

追溯除法，最早是在“平均分”的问题背景下产生的。关于平均分的含义，一般认为：在人们分物的时候，常常要求做到“公平”，因而在“分”的时候，要“分”得“同样多”，“平均分”由此而产生。即在分物时，使得每份所分得的数量都相等。我们知道，日常平均分物有两种情况：一是知道要分的总数和平均分的份数，求每份数是多少，即“等分除”；二是知道要分的总数和每份数，求平均分的份数，即“包含除”。这两种不同情况的除法都是在“平均分”的数学模型中产生的，地位平等。以北师大版教材编排为例，学生第一次认识除法是在二年级上册第七单元“分一分与除法”中，教材用三个课时让学生充分经历了“平均分物”的各种活动，之后又通过第四课时“分香蕉”的实例把直观操作符号化、数学化，引导学生认识除法。无论是前面的“平均分物”还是后面的“认识除法意义和除法算式”，北师大版教材都淡化了对除法“等分除”和“包含除”的两层意义的教学，即在认识除法的开始阶段对二者不作区分。教材认为，两者的本质是一致的，都是把一个整体分成若干相同的部分，这里的部分就是“一份数”，这里的若干就是“份数”，这其中的数量关系就是“总数”与“一份数”和“份数”的关系。所谓“等分除”与“包含除”的不同就是“知道总数和份数求每份数”和“知道总数和每份数求份数”而已。教学中应引导学生体会不同情境下具有的数学本质，即把一个整体分成若干相同的部分，为后续引入除法和理解除法的意义积累丰富的现实素材和活动经验。学生由此体验到：只要是把一个整体平均分成若干部分，这个活动过程就可以用除法来表示。换言之，在学习除法的起始阶段，教材是有意把“包含除”蕴含在“平均分”的问题情境中，与“等分除”不作区分，认为这只是“平均分”的两种情况（如图2）。

图2

教材的这种模糊处理，笔者并不认同。笔者更认同张奠宙教授的说法：除法教学，最常见的情境是“平均分物”，如将一些饼干平均分给小朋友。这一数学模型，涉及两种除法，即“等分除”和“包含除”。“等分除”和“包含除”是同一个数学模型的两个侧面。我们不但要区分“等分除”和“包含除”，还要把二者明确地说出来，写进教学用书，甚至写入教材，目的是让学生完整地了解除法的数学模型。

2.扩充至“倍”的认识，拓展至“包含除”的意义

按照北师大教材的呈现顺序，教材意在结合“倍的认识”，引导学生加深对除法“包含除”含义的理解。本单元的第六课时“倍的认识”结合除法进行学习，只是“倍”不作为科学概念而只作为生活概念来处理，即结合具体情境和问题解决的过程让学生体会“倍”的意义，感受倍与除法的联系，进而拓展除法的意义（如图3）。

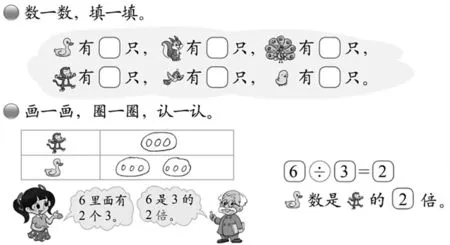
图3

从教材的编排来看，对“倍”的理解实际上就是对除法意义的拓展，即除法不仅可以表示一个数量的“等分除”问题，也可以表示两个数量之间的关系（倍数关系）。而这里的“两个数量之间的倍数关系”其实就是除法的“包含除”的意义，即a 的数量是b 的数量的多少倍，就是指a 的数量里包含有多少个b的数量，也就是把b的数量看作“一份数”，那么“倍数”就是“份数”。也可以从度量的角度加以审视，即把b 的数量看作一个标准度量单位（一份数），去度量a的数量（总数），度量的次数（份数）就是“倍数”。由此可见，除法学习至此，除法的意义已经由表示一个数量“等分除”的问题扩充至两个数量“包含除”的倍数关系问题，随着对除法学习的再认识，除法的意义在学生的认知结构层次上实现了新的拓展与提升。

3.再谈明晰“等分除”与“包含除”对除法学习的重要性

诚然，“等分除”是把一个总数平均分成若干份，求每一份的数量是多少；“包含除”是把每一份的数量看作一个标准量，看总数里有几个这样的“一份数”，相当于把总数平均分成了几份。这样看，无论是“等分除”还是“包含除”，单从学习活动上看是基本一样的，都可以看作是把一个整体数量分成若干相同的部分的过程。但是，从问题情境数学化的角度来看，“等分除”和“包含除”还不完全是一回事。他们不仅仅是简单的“平均分”的两种方式，也不仅仅是“平均分”的不同分法，它们客观再现的数学问题的本质意义和学生的思维认知存在着明显差别。在除法学习的起始阶段，基于学生对除法理解的初步程度，如教材所述可以将“包含除”的问题蕴含于“平均分”中暂时与“等分除”不作区分。但随着除法学习的深入，随着学习内容的不断进阶，学生对除法意义的认识也需要进一步扩充和拓展，这就是“倍的认识”出现的重要意义。“倍的认识”使得学生对除法意义的理解由统一一个数量的“等分除”上升为两个数量的“包含除”的倍数关系，将“包含除”的意义从“等分除”中剥离出来，既是对不同问题情境数学化抽象理解的体现，也是学生对除法意义认知结构逐步完善的体现。

让我们再来看两个例子。

问题1：国内长途每分钟0.3 元，笑笑打电话通话费用了5.1元，笑笑打电话的时间是多少分钟？

显然，这两个例子是“小数除法”和“分数除法”的问题。在“用除法解决这样的问题”以及解释“为什么用除法解决”时，一般用“等分除”不好解释，而用“包含除”的意义或“倍”的关系来解释则学生很容易理解，即“要求打电话的时间是多少分钟，就是看5.1元里有多少个0.3元”“要求可以吃多少天，就是看20kg 里有多少个，从两个量之间的数量关系来理解除法正是除法“包含除”的意义。这也正说明，从整数到小数再到分数，随着数系的不断扩展，学生对除法的学习也会随之从整数除法到小数除法再到分数除法不断深化，对运算意义的理解与再认识也会随之更加清晰、明朗和走向深入。

（二）延伸再认识乘法意义的扩充拓展问题

追溯乘法，最初是表示“求几个相同加数的和”，即用相同加数乘相同加数的个数。但随着数系领域的不断扩展，这里的加数也逐渐开始突破自然数的限制。比如“小数乘整数”“分数乘整数”，这里乘法的最初定义已经无法“双向”解释，乘法意义需要进一步扩充拓展。随着乘法的认识和学习，乘法也出现了倍的意义，即求一个数的几倍是多少。从整数乘法到小数乘法中的“小数乘小数”，再到分数乘法中的“整数乘分数”“分数乘分数”。这一过程中乘法意义又突破了“倍”的意义，与“分数意义”相关联，进一步完成了由表示“几个几”到表示“一个数的几分之几”的扩充与拓展。由此可见，小数乘法、分数乘法的意义与整数乘法的意义已经并不完全相同，有时用整数乘法的意义“几个几”可以解释，有时却需要联系分数的意义解释才更科学合理。乘法运算的意义必须根据学习内容进行扩充和拓展。

三、运算教学：运算意义应从固有的“原始性认识”向整体的“结构性认识”转变进阶

回应前面观课中的问题。“案例”的内容是根据问题情境提出用除法解决的实际问题，是在学生经历了第一阶段“分一分与除法”的学习，已经认识了除法“等分除”的意义，并进一步通过“倍的认识”补充拓展了“包含除”的意义的基础上展开的第二阶段除法学习。因此根据学习内容的进阶，在将问题情境数学化的过程中还是需要将“包含除”与“等分除”区分开来，帮助学生全面补充拓展理解除法的意义。正如张奠宙教授所言“在日常生活中，‘等分除’情境与‘包含除’情境是不一样的，虽然都归于除法，但只有把两者意义区分开，除法模型才会建立得更加丰满”。

综上所述，运算意义的教学不应也不能是“一以贯之”，而是要根据学习内容的进阶“扩充拓展”，不断丰富完善学生对运算意义理解的认知结构。就整体而言，我们不仅应当高度重视对运算意义固有的“原始性认识”，努力促使学生向整体的“结构性认识”转变进阶，而且应帮助学生根据数系的不断扩展以及运算内容、学习阶段的进阶遵从知识学习的本质规律，从更高层次上进行思维与认识水平的必要重构，从而完成对运算意义理解的发展与深化。