Orlicz混合宽度积分①
2022-06-28杨林唐孝国谭杨罗淼
杨林, 唐孝国, 谭杨, 罗淼
1.铜仁职业技术学院 信息工程学院,贵州 铜仁 554300;2.贵州师范大学 数学科学学院,贵阳 550025
Orlicz-Brunn-Minkowski理论[1-3]基于LpBrunn-Minkowski理论[4]发展而来,在凸体或星体(及其相关的如投影体、 相交体等)的体积、混合体积、仿射表面积、宽度积分及弦长积分等研究目标上建立了Orlicz-Minkowski不等式、Orlicz-Brunn-Minkowski不等式及其他一系列优美的结果[5-11]. 近期关于平面上的凸体或凸曲线的研究可参见文献[12-14].

设K∈Kn的支撑函数h(K,·)为
h(K,u)=max{x·u:x∈K}u∈Sn-1
K的n维体积为
dS(K,u)表示K在u方向上的面积微元,K的宽度函数为
若存在正实数λ,使得b(K,u)=λb(L,u),则称K与L具有相似宽度.

确定.
由Orlicz组合的定义可知
同时建立了一系列不等式,如Orlicz-Aleksandrov-Fenchel不等式和Orlicz Brunn-Minkowski不等式:

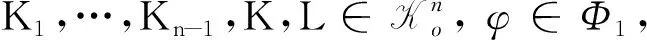
文献[14]研究了K1,…,Kn∈Kn的混合宽度积分B(K1,…,Kn),其积分表达式为
(1)
并建立了不等式
(2)
设α,β为非负且不同时为0的实数,文献[10]定义并研究了K,L∈Kn的Orlicz宽度线性加法b(+φ(K,L,α,β),u),
其中
φ(x,y)=φ1(x)+φ2(y)φ1,φ2∈Φ1
由Orlicz宽度线性加法的定义可知
(3)
设K,L∈Kn,φ∈Φ1,0≤i (4) 同时建立了如下Orlicz Minkowski不等式和Orlicz Brunn-Minkowski不等式: Orlicz-Minkowski不等式若K,L∈Kn,φ∈Φ1,0≤i 等号成立当且仅当K与L具有相似宽度. Orlicz Brunn-Minkowski不等式若K,L∈Kn,φ∈Φ2,0≤i 等号成立当且仅当K与L具有相似宽度. 本文在文献[9-10]的启发下,定义了关于K1,…,Kn-1,K,L的Orlicz多元混合宽度积分Bφ(K1,…,Kn-1,K,L),其表达式为 (5) 当K1,…,Kn-1中有n-i-1个与K相等,其余i个为单位球时,(5)式即为公式(4). 本文建立了Orlicz多元混合宽度积分的如下不等式: 定理1若K1,…,Kn-1,K,L∈Kn,φ∈Φ1,则 等号成立当且仅当K与L具有相似宽度. 定理2若K1,…,Kn-1,K,L∈Kn,φ∈Φ2,α,β>0,则 等号成立当且仅当K与L具有相似宽度. 为得到文中结论的证明,需借助以下引理: 引理2若K,L∈Kn,φ=φ(x,y)=φ1(x)+φ2(y),φ1,φ2∈Φ1,则 证由引理1、(3)式及凸函数的性质知 其中 引理3若K1,…,Kn-1,K,L∈Kn,φ∈Φ2,则 证由引理1、 引理2、 (1)式,令 f(u)=b(K1,u) …b(Kn-1,u) 可以得到 由引理3与Bφ(K1,…,Kn-1,K,L)的定义,可得: 引理4设K1,…,Kn-1,K,L∈Kn,φ∈Φ1,则 等号成立当且仅当f(u)=C(a.e.x∈X),其中C为常数. 定理1的证明由引理4、 引理5及(1)式可得 (6) 由引理5不等式等号成立的条件知定理1中不等式等号成立的充要条件为K与L具有相似宽度. 由定理1、不等式(2)以及φ的单调递减性可得: 推论1若K1,…,Kn-1,K,L∈Kn,φ∈Φ1,1≤m 等号成立当且仅当K与L具有相似宽度. 在推论1中令φ(x)=x-p,可得: 推论2若K1,…,Kn-1,K,L∈Kn,1≤m 等号成立当且仅当K与L具有相似宽度. 当推论1中,当m=n-1时,有: 推论3若K1,…,Kn-1,K,L∈Kn,φ∈Φ1,则 等号成立当且仅当K与L具有相似宽度. 定理2的证明由(1),(3)式与引理4,令 C=(K1,…,Kn-1) 可得 整理即得 由定理1不等式等号成立的条件知定理2中不等式等号成立当且仅当K与L具有相似宽度. 由定理2、不等式(2)以及φ的单调性,可得: 推论4若K1,…,Kn-1,K,L∈Kn,φ∈Φ2,1≤m 等号成立当且仅当K与L具有相似宽度. 在定理2中令φ(x,y)=x-p+y-p,得: 推论5若K1,…,Kn-1,K,L∈Kn,p≥1,则 B(K1,…,Kn-1,+p(K,L,1,1))-p≥B(K1,…,Kn-1,K)-p+Bφ(K1,…,Kn-1,L)-p 等号成立当且仅当K与L具有相似宽度.


