我国新凯恩斯菲利普斯曲线的经验研究

戴晓兵 李志超

摘 要：本文基于1991—2020年的季度数据，通过构建适应性学习预期的状态空间模型，采用卡尔曼滤波算法对我国学习型预期进行了测度，并将适应性学习预期、高阶滞后适应性预期、理性预期和混合预期分别代入新凯恩斯菲利普斯曲线进行经验研究，进而分析我国新凯恩斯菲利普斯曲线的混合学习预期特征。研究结果表明：首先，我国适应性学习预期并非完全理性预期，而是一种近理性预期，具有近理性特征。其次，我国新凯恩斯菲利普斯曲线具有高阶滞后适应性预期与适应性学习预期的混合学习预期特征，同时高阶滞后预期对通胀率的影响表现为逆向的通胀惯性。最后，适应性学习预期特征要强于高阶滞后适应性预期特征，即相比于高阶滞后适应性预期，适应性学习预期可以更好地反映我国通胀预期形成机制，但适应性学习预期相对于高阶滞后适应性预期的强度受通胀率衡量指标的影响。

关键词：新凯恩斯菲利普斯曲线;混合学习预期;适应性预期;适应性学习预期;高阶滞后适应性预期;卡尔曼滤波

中图分类号：F822.5  文献标识码：A

文章编号：1000-176X（2022）04-0055-10

2019年下半年，我国整体宏观经济已表现出由弱企稳的增长趋势，實际CPI通胀率也低于通胀目标水平，尽管政府公布的2020通胀率目标水平略高一点为3.5%，但实际CPI通胀率仍低于3%。一方面，是由于稳健的宏观经济调控政策;另一方面，也反映了国内公众通胀预期较为稳定。央行从2010年开始加强通胀调控，2011年首次将稳定通胀预期和控制通胀率作为货币政策的首要目标，尤其是在通胀压力较大时期更加注重通胀预期管理。（例如，2011年第一季度、2019年第四季度）。作为货币政策传导机制之一的新凯恩斯菲利普斯曲线能够较好地刻画通胀与产出缺口和通胀预期的关系，因而成为各国央行制定货币政策的重要参考，这意味着如果能够准确刻画通胀率与产出缺口的权衡关系，央行可以通过调控产出缺口来实现通胀目标。但通胀预期会影响通胀率与产出缺口的权衡关系，因而合理评估通胀预期成为估计新凯恩斯菲利普斯曲线的关键。我国通胀预期具有怎样的特征，是否具有近理性的学习型特征以及如何评估我国的学习型预期？受通胀预期影响，我国新凯恩斯菲利普斯曲线具有纯粹预期特征还是混合预期特征，如果具有混合预期特征，那么是哪些预期的混合呢？本文正是基于上述问题，对我国通胀预期的学习型特征以及附带混合学习预期的新凯恩斯菲利普斯曲线展开经验研究。

一、文献综述

理性预期学派代表Lucas[1]指出，适应性预期会产生系统误差，建议用理性预期替代适应性预期，且从理性预期的角度得到的菲利普斯曲线不论在短期还是在长期都是垂直的。Taylor [2]则对菲利普斯曲线做了改进，认为在粘性价格下，即使企业可以根据获得的一切信息实现理性预期，菲利普斯曲线在短期也是倾斜的。那么菲利普斯曲线中的理性预期假设是否是合理的呢？Evans[3]认为，理性预期学派对预期的假设过于严格，放松理性预期假设将其转变为适应性学习预期假设会更加符合公众预期的形成机制。Cogley和Sargent[4]同样建议使用适应性学习预期的形成方式来代替理性预期。在Evans和Honkapohja[5]提出预期形成的适应性学习理论的基础上，相关文献开始关注学习型预期的微观基础。Orphanides和Williams [6]通过对预期形成和参数调整机制的刻画，使得公众的通胀预期得以内生化，而且通过控制学习过程的相关参数，适应性学习预期可以较好地刻画预期的有限理性内涵。Milani[7-8]发现，学习行为是通胀持久性的主要来源，前瞻性因素在通胀动态中起更重要的作用。Zhang和Kim[9]基于通胀预期调查数据和近似理性预期进行了研究证实，前瞻性行为在通胀驱动中作用较小。Sousa和Yetman[10]发现，新兴经济体的央行制定政策也越来越依靠预期变量，通过分析通胀预期的影响因素比较了不同通胀预期测算方法的差异，并发现新兴经济体通胀预期稳定态势呈现逐渐加强的趋势。Coibion等[11]通过随机对照实验研究了不同形式的沟通如何影响个体的通胀预期发现，影响公众通胀预期形成的相关信息更多来自权威新闻且经济主体获取信息具有很强的自主性。

国内关于通胀预期的研究主要集中在我国通胀预期的测度和新凯恩斯菲利普斯曲线的特征方面。对通胀预期的测度方法大体分为三类：一是统计调查法。通过对公众进行问卷调查，获取公众对未来通胀的判断数据。如黎文靖和郑曼妮[12]将央行定期发布的储蓄问卷调查报告数据用滚动方法进行OLS回归，算出预期通胀率。何启志和姚梦雨[13]将学习型预期与调查问卷法结合起来，提出了递归法和滚动法两种通胀预期测度方法。二是金融市场价格法。选取金融市场中相关指标对未来通胀率进行预测。如姚余栋和潭海鸣[14]利用卡尔曼滤波法，建立无套利仿射模型，从利率期限结构中分解出中长期通胀预期。三是模型估算法。利用宏观经济模型或计量模型等估计通胀预期。如卞志村和高洁超[15]基于常系数最小二乘法的固定收益学习模型对适应性学习预期进行了估算。国内学者也对我国新凯恩斯菲利普斯曲线的预期特征进行了广泛研究，近期研究认为，很多学者认为，我国菲利普斯曲线具有惯性特征、混合预期特征或学习型预期特征。如李昊和王少平[16]发现，我国通胀形成机制具有理性预期与适应性预期相混合的特征。卞志村和胡恒强[17]则基于粘性信息给出了我国菲利普斯曲线具有混合预期特征的一个微观解释。何启志和范从来[18]则发现，我国新凯恩斯菲利普斯曲线具有学习型预期特征。

适应性学习预期假设公众能够基于历史信息不断调整和更新预期行为，从而使得通胀预期逐渐趋于理性预期。相对于纯粹理性预期，具有适应性学习预期的公众在得到更新信息时会立即调整自身行为，使得通胀预期趋于理性而并非完全理性，更符合公众预期的形成方式，且体现了公众对于当期与预期信息的有限可得性。相对于纯粹适应性预期，具有适应性学习预期的公众考虑到了所有滞后通胀率包含的历史信息，而非仅依赖一阶滞后通胀率，体现了公众对历史信息的完全可得性。因此，适应性学习预期可以更好地刻画公众通胀预期的形成过程。从现有研究结论可以看出，我国新凯恩斯菲利普斯曲线具有混合预期特征和学习型预期特征，但并未将混合预期与学习型预期联系起来，本文的研究结果表明，我国新凯恩斯菲利普斯曲线具有混合学习预期的特征。

本文的创新之处主要体现在两个方面：一是基于卡尔曼滤波算法的适应性学习理论引入通胀预期测度中，并对我国通胀预期的认知偏差、无偏性和有效性进行检验。二是分别将理性预期和适应性预期与学习型预期组成混合预期，经验分析了我国新凯恩斯菲利普斯曲线的混合学习预期特征。

本文结构安排如下：第二部分为研究设计，包括卡尔曼滤波适应性学习方程、单一预期与混合学习预期菲利普斯曲线模型的设定;第三部分为我国适应性学习预期的估计及检验，包括基于卡尔曼滤波适应性学习方程测度通胀预期，并进行认知偏差、无偏性和有效性检验;第四部分为我国混合学习新凯斯菲利普斯曲线的估计，包括基于适应性学习预期、适应性预期和理性预期，以及由适应性学习预期和其他两种预期组合成混合学习预期对我国菲利普斯曲线的具体形式进行经验分析;第五部分为主要结论与政策建议。

二、研究设计

（一）卡尔曼滤波适应性学习方程的设定

假定公众对通胀预期π*t与实际通胀率πt的关系为：

πt=π*t+ε1t（1）

其中，ε1t为预期误差。在适应性学习规则下，公众在形成通脹预期时会参考历史通胀预期π*t-i及通胀率的均值，即：

ln（π*t）=ρ1ln（π*t-1）+ρ2ln（π*t-2）+ρ3ln（π*t-3）+（1-ρ1-ρ2-ρ3）ln（）+ε2t（2）

将模型（2）在π*t=1处做一阶泰勒展开有：

π*t=1+ρ1（π*t-1-1）+ρ2（π*t-2-1）+ρ3（π*t-3-1）+（1-ρ1-ρ2-ρ3）ln（）+ε2t（3）

将模型（1）和模型（3）分别作为观测方程和状态方程，则通胀预期的适应性学习方程可以写成下面的状态空间模型：

ξt=ct+Tξt-1+vt

Pt=Hξt+ut（4）

其中，H=100000000，ct=（1-ρ1-ρ2-ρ3）ln（）ln（）ln（），T=ρ1ρ2ρ3100010，ut=（ε1t，0，0），Pt=（πt，0，0），ξt=（π*t，π*t-1，π*t-2）T，vt=（ε2t，0，0）。本文通过卡尔曼滤波算法估计状态空间模型（4），进而得到适应性学习预期π*t。

（二）新凯恩斯菲利普斯曲线的设定

新凯恩斯菲利普斯曲线的基准形式为：

πt=βπet+λyt+εt（5）

其中，λ为通胀与产出缺口的权衡系数，β为预期增广系数，εt为随机误差项。设定πet存在三种预期形式：

首先，高阶滞后适应性预期。将各阶滞后通胀率乘以一定的权重并加总求和，即πet=Et-1πt=∑kj=1β0，jπt-j。

其次，适应性学习预期。将基于卡尔曼滤波算法得到的通胀预期作为适应性学习预期，即πet=π*t。

最后，理性预期。通常采用下一期实际通胀率作为当期通胀率的理性预期，即πet=Etπt+1=πt+1。为更全面地分析我国新凯恩斯菲利普斯曲线的形式，本文分别将三种预期以及将适应性学习预期与理性预期、适应性学习预期与高阶滞后预期的混合预期代入模型（5）进行经验分析。因此，本文经验分析的新凯恩斯菲利普斯曲线共五种形式，分别为：

πt=∑kj=1β0jπt-j+λyt+εt（6）

πt=β1π*t+λyt+εt（7）

πt=β2Etπt+1+λyt+εt（8）

πt=β1π*t+β2Etπt+1+λyt+εt（9）

πt=∑kj=1β0jπt-j+β1π*t+λyt+εt（10）

（三）变量选取与数据处理

本文选取我国季度经济数据进行参数估计，这是因为年度数据较少，不能反映每年数据变化的具体情况，影响模型估计的有效性，而月度数据的波动性较大，影响模型估计的稳定性。所有数据均来自中经网统计数据库。

在通胀率衡量指标的选择上，常用的指标有消费者价格指数CPI、生产者价格指数PPI和GDP平减指数等。PPI是反映生产企业提供的商品价格在一定时期内变化程度的指标，但其未将劳务产品的变化包含在内，因而不能全面反映出物价的变化。GDP平减指数的编制是以年为单位的，不能反映作为季度通胀率的变化程度，且数据样本容量较小，不能得出参数的有效估计量。因此，本文选择CPI作为通胀率的衡量指标，同时采用商品零售价格指数RPI进行稳健性检验。数据选取1991年1季度至2020年4季度的实际季度通胀率。由于CPI和RPI均为月度数据，需要将其加权平均转化为季度数据，同时为缩短价格变化周期，本文没有采用同比数据，而是采用季度环比数据进行研究。由于官方公布的CPI在1991—2000年、RPI在1991—2002年为同比数据，因而需要将同比数据转化为环比数据。

本文还选取了固定资产投资额、社会消费品零售总额、进出口差额、流通中的现金M0、货币与准货币M2、实际通胀率、全国银行间同业拆借市场7天加权平均利率和人民币对美元的平均汇率等经济系统中的其他变量，对我国适应性学习预期的有效性进行检验。鉴于部分数据的时间可得性，选择2003—2020年的经济数据进行检验。

在产出缺口的估计上，常用方法有生产函数法和趋势分解法两种，包括线性趋势法、HP滤波法以及单变量和多变量的卡尔曼滤波法等。本文采用HP滤波法对产出缺口进行估计。其一，为避免通胀影响，将名义GDP转换为实际GDP，以CPI为基础的实际GDP1=名义GDP/（1+CPI），以RPI为基础的实际GDP2=名义GDP/（1+RPI）。其二，为避免季节效应的影响，采用X12方法对实际GDP1和实际GDP2进行季节调整。其三，利用HP滤波法得到以CPI为基础的产出缺口GDP_GAP1和以RPI为基础的产出缺口GDP_GAP2。

三、我国适应性学习预期的估计及检验

（一）我国适应性学习预期的卡尔曼滤波估计

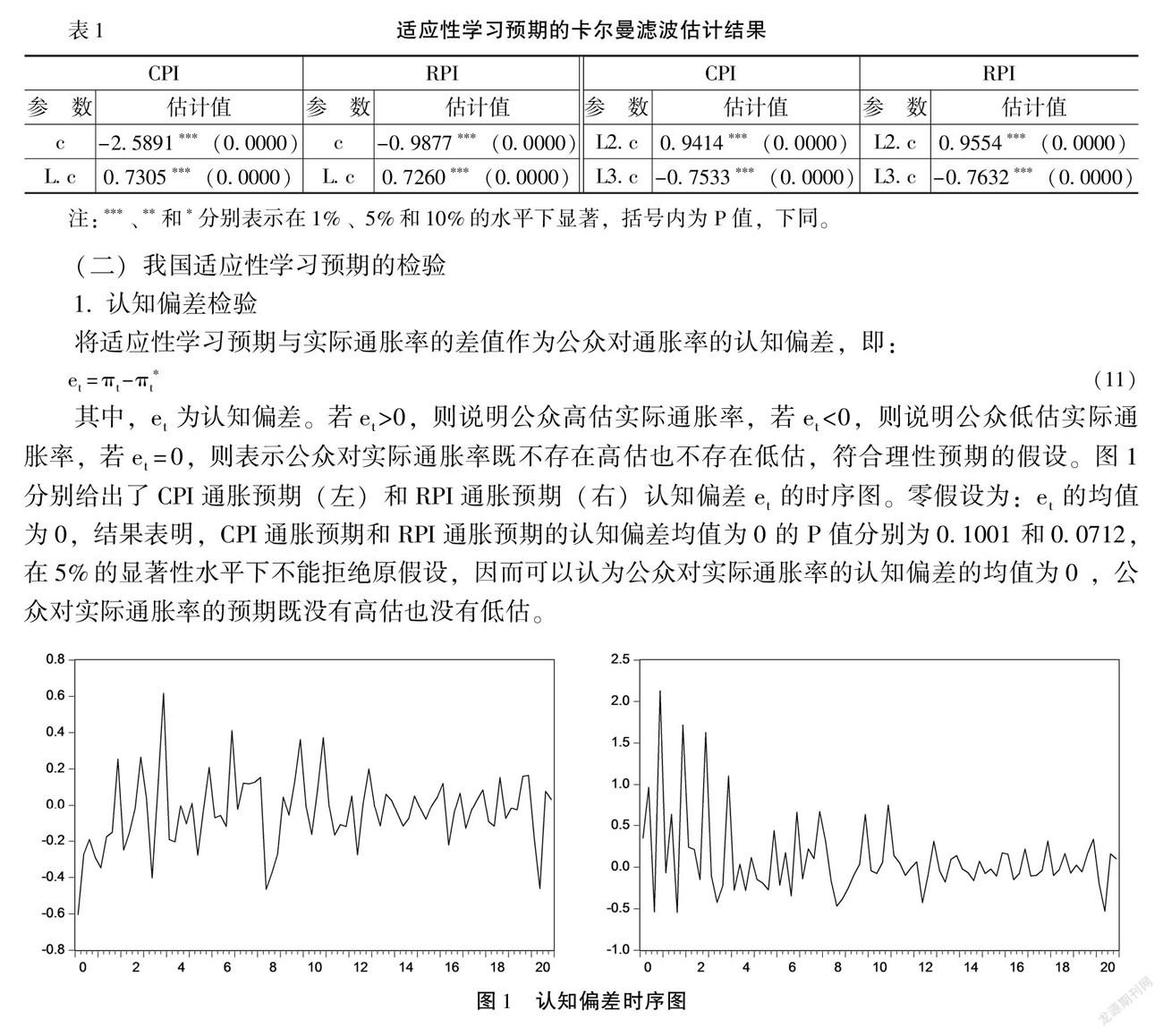
表1给出我国适应性学习预期的卡尔曼滤波估计结果。，图1给出了实际通胀率与估计的预期通胀率的时序图（左边为CPI通胀率，右边为RPI通胀率）。由表1可知，当用CPI衡量通胀预期时，滞后一期的预期、滞后二期的预期和滞后三期的预期对当期预期的影响程度分别为0.7305、，滞后二期的预期对当期预期的影响程度为0.9414和-0.7533，通胀均值对当期预期的影响程度为0.0814。当用RPI通胀预期时，滞后一期的预期、滞后二期的预期和滞后三期的预期对当期预期的影响程度分别为0.7260、0.9554和-0.7632，通胀均值对当期预期的影响程度为0.0818。可见，滞后通胀预期对当期预期的影响存在显著差别，滞后一、二期通胀预期对当期预期存在正向影响，滞后三期通胀预期对当期预期存在负向影响，且通胀均值对当期预期的影响较小。

（二）我国适应性学习预期的检验

1.认知偏差检验

将适应性学习预期与实际通胀率的差值作为公众对通胀率的认知偏差，即：

et=πt-π*t（11）

其中，et为认知偏差。若et>0，则说明公众高估实际通胀率，若et<0，则说明公众低估实际通胀率，若et=0，则表示公众对实际通胀率既不存在高估也不存在低估，符合理性预期的假设。图1分别给出了CPI通胀预期（左）和RPI通胀预期（右）认知偏差et的时序图。零假设为：et的均值为0，结果表明，CPI通胀预期和RPI通胀预期的认知偏差均值为0的P值分别为0.1001和0.0712，在5%的显著性水平下不能拒绝原假设，因而可以认为公众对实际通胀率的认知偏差的均值为0 ，公众对实际通胀率的预期既没有高估也没有低估。

表2给出了CPI通胀预期和RPI通胀预期认知偏差自相关系数、偏自相关系数及其检验值。由表2可知，认知偏差前几阶的自相关系性比较明显，但是随着阶数的滞后，认知偏差自相关性较为显著的情况就会消失，根据Cuckierman和Meltzer[19]，如果公众对通胀预期的误差只在有限阶数内存在相关性，则不能否认公众预期为理性预期，因为具有完全理性的公众对通胀预期也会出现这种情况，因而可以认为适应性学习预期的认知偏差符合理性预期的要求。同时，CPI通胀率只有2、6阶偏自相关系数落在两倍标准差之外，RPI通胀率只有4阶偏自相关系数落在两倍标准差之外，其余阶数的偏自相关系数均不显著，即当期公众基于t期信息所得到的通胀预期认知偏差，在保证k期信息不变的条件下，与t+k期的认知偏差无相关性，即公众在得到历史信息以后，对将来任意两期的认知偏差均可以近似看成与历史信息不相关，可以进一步认为适应性学习预期认知偏差符合理性预期要求。

2.无偏性检验

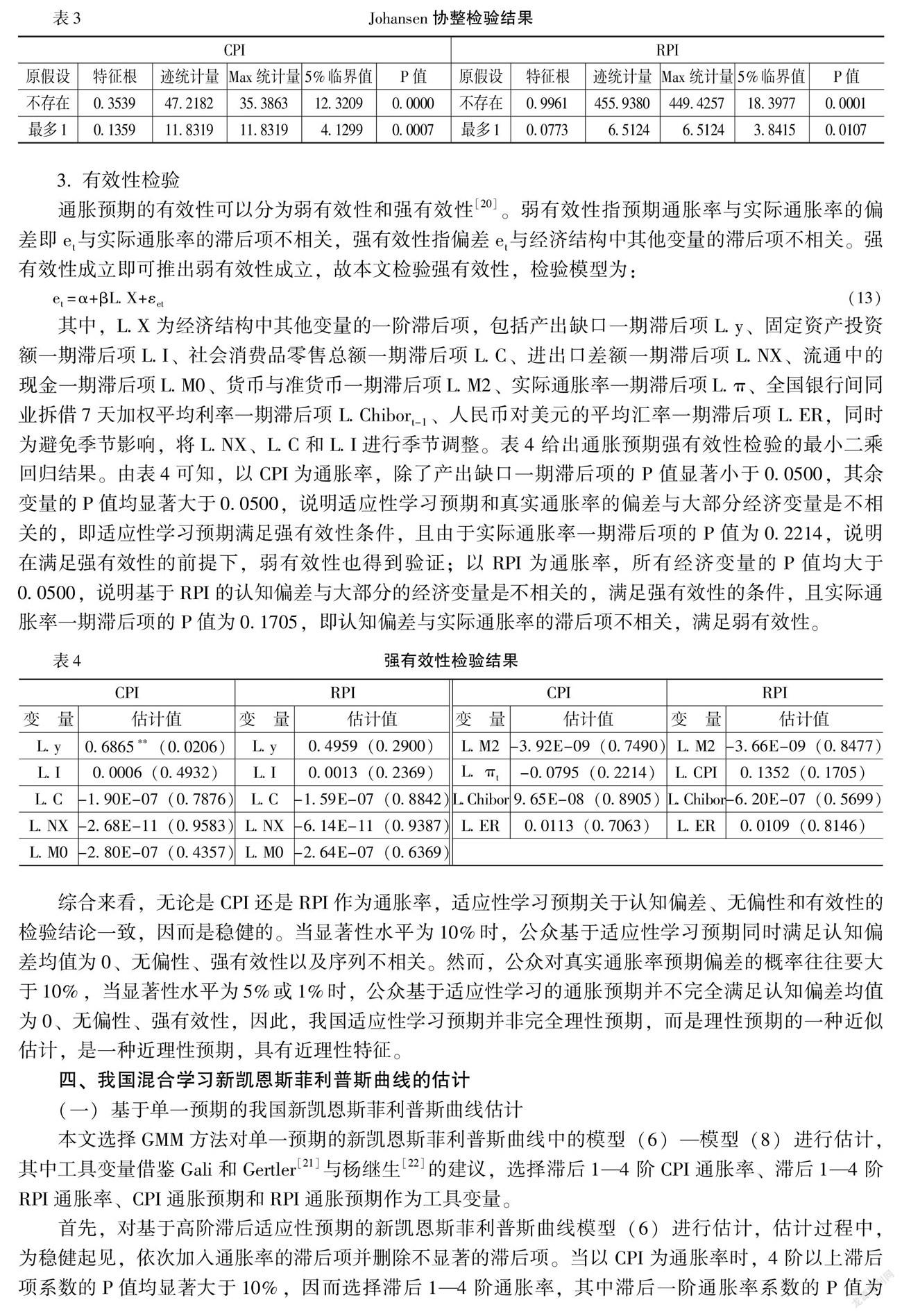
本文采用协整方法检验适应性学习预期的无偏性。一是对实际通胀率和预期通胀率进行ADF检验，结果表明在5%的显著性水平下，实际通胀率和预期通胀率均为不平稳序列，其一阶差分均为平稳序列，即二者均服从一阶单整。二是利用Johansen协整检验来判断二者是否存在协整关系。表3给出了Johansen协整检验结果，由表3可知，迹统计量和Max统计量的值均大于5%临界值，P值均小于5%，因而实际通胀率与预期通胀存在长期均衡的协整关系。三是进行协整估计，实际通胀率与预期通胀率的无偏关系式可以表示为：

πt=β0+β1π*t+ut（12）

其中，β0为截距项，β1为无偏系数，ut为服从白噪声的误差项。无偏性原假设为：β0=0、β1=1。表4给出了模型（12）的协整估计结果。由表4可知，无论是CPI还是RPI作为通胀率，截距项的P值均大于0.0500，即在5%的显著性水平下截距项的估计值不显著，无偏系数的P值均趋于0，因而非常显著。进一步，对无偏系数约束条件β1-1=0作Wald系数检验，结果显示，无论是CPI还是RPI作为通胀率，F值和卡方统计量的P值均远大于0.0500，即在5%的显著性水平下无偏显示的估计值显著为1。因此，适应性学习预期是真实通胀率的无偏估计。

3.有效性检验

通胀预期的有效性可以分为弱有效性和强有效性[20]。弱有效性指预期通胀率与实际通胀率的偏差即et与实际通胀率的滞后项不相关，强有效性指偏差et与经济结构中其他变量的滞后项不相关。强有效性成立即可推出弱有效性成立，故本文检验强有效性，检验模型为：

et=α+βL.X+εet（13）

其中，L.X为经济结构中其他变量的一阶滞后项，包括产出缺口一期滞后项L.y、固定资产投资额一期滞后项L.I、社会消费品零售总额一期滞后项L.C、进出口差额一期滞后项L.NX、流通中的现金一期滞后项L.M0、货币与准货币一期滞后项L.M2、实际通胀率一期滞后项L.π、全国银行间同业拆借7天加权平均利率一期滞后项L.Chibort-1、人民币对美元的平均汇率一期滞后项L.ER，同时为避免季节影响，将L.NX、L.C和L.I进行季节调整。表4给出通胀预期强有效性检验的最小二乘回归结果。由表4可知，以CPI为通胀率，除了产出缺口一期滞后项的P

值显著小于0.0500，其余变量的P值均显著大于0.0500，说明适应性学习预期和真实通胀率的偏差与大部分经济變量是不相关的，即适应性学习预期满足强有效性条件，且由于实际通胀率一期滞后项的P值为0.2214，说明在满足强有效性的前提下，弱有效性也得到验证;以RPI为通胀率，所有经济变量的P值均大于0.0500，说明基于RPI的认知偏差与大部分的经济变量是不相关的，满足强有效性的条件，且实际通胀率一期滞后项的P值为0.1705，即认知偏差与实际通胀率的滞后项不相关，满足弱有效性。

综合来看，无论是CPI还是RPI作为通胀率，适应性学习预期关于认知偏差、无偏性和有效性的检验结论一致，因而是稳健的。当显著性水平为10%时，公众基于适应性学习预期同时满足认知偏差均值为0、无偏性、强有效性以及序列不相关。然而，公众对真实通胀率预期偏差的概率往往要大于10%，当显著性水平为5%或1%时，公众基于适应性学习的通胀预期并不完全满足认知偏差均值为0、无偏性、强有效性，因此，我国适应性学习预期并非完全理性预期，而是理性预期的一种近似估计，是一种近理性预期，具有近理性特征。

四、我国混合学习新凯恩斯菲利普斯曲线的估计

（一）基于单一预期的我国新凯恩斯菲利普斯曲线估计

本文选择GMM方法对单一预期的新凯恩斯菲利普斯曲线中的模型（6）—模型（8）进行估计，其中工具变量借鉴Gali和Gertler[21]与杨继生[22]的建议，选择滞后1—4阶CPI通胀率、滞后1—4阶RPI通胀率、CPI通胀预期和RPI通胀预期作为工具变量。

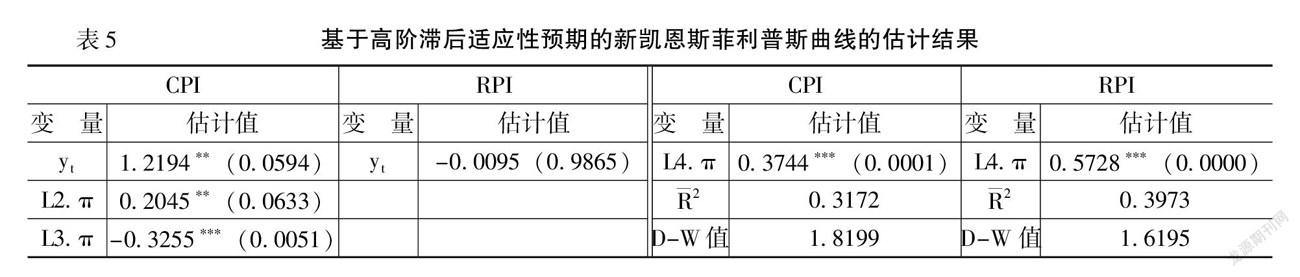
首先，对基于高阶滞后适应性预期的新凯恩斯菲利普斯曲线模型（6）进行估计，估计过程中，为稳健起见，依次加入通胀率的滞后项并删除不显著的滞后项。当以CPI为通胀率时，4阶以上滞后项系数的P值均显著大于10%，因而选择滞后1—4阶通胀率，其中滞后一阶通胀率系数的P值为0.4905，参数估计值不显著，因而删除重新估计，表5给出了估计结果。由表5可知，滞后2—3阶通胀率的系数、产出缺口与通胀率的权衡系数至少在10%水平下均显著。

当以RPI为通胀率时，4阶以上滞后项系数的P值均显著大于10%，因而选择滞后1—4阶通胀率，其中滞后1—3阶通胀率的系数估计值不显著，因而选择滞后4阶通胀率进行估计。结果显示，产出缺口与通胀率的权衡系数不显著，这与CPI为通胀率的结论不一致，但4阶滞后项系数显著至少说明我国新凯恩斯菲利普斯曲线具有高阶滞后适应性预期的特征。

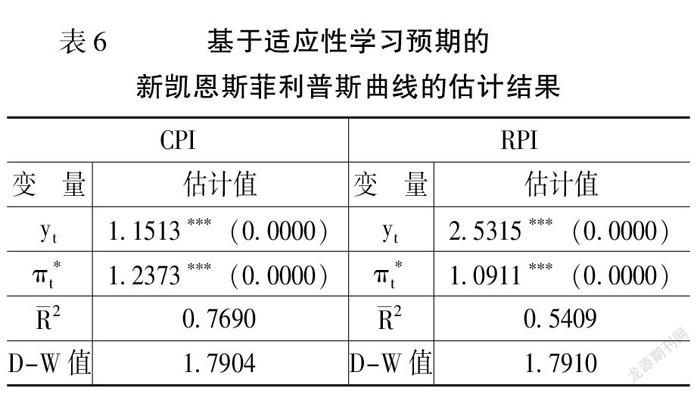
其次，对基于适应性学习预期的新凯恩斯菲利普斯曲线模型（7）进行估计，如表6所示。由表6可知，当以CPI为通胀率时，产出缺口与通胀率的权衡系数显著大于0，且模型拟合优度显著大于模型（6），因而模型（7）较优，同时适应性学习预期的系数为正值且P值趋于0，说明适应性学习预期对当期通胀率存在显著的正向影响。当以RPI为通胀率时，产出缺口与通胀率的权衡系数和适应性学习预期系数均显著，与前述结论一致。相对于高阶滞后适应性预期，适应性学习预期可以更好地刻画通胀预期对当期通胀率的影响，因而我国新凯恩斯菲利普斯曲线还具有适应性学习预期的特征。

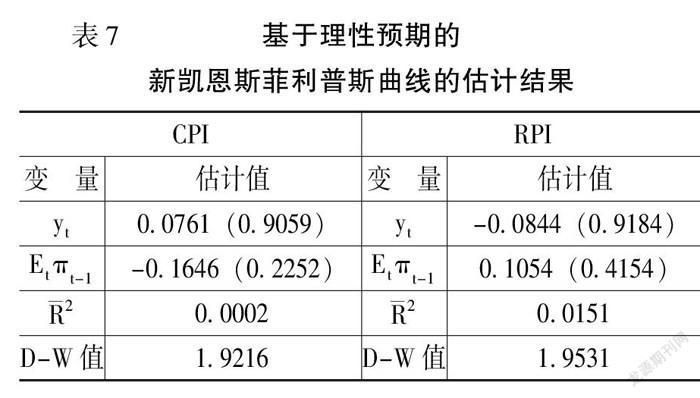
最后，对基于理性预期的新凯恩斯菲利普斯曲线模型（8）进行估计，如表7所示。由表7可知，无论是以CPI为通胀率还是以RPI为通胀率，产出缺口与通胀率的权衡系数、理性预期系数均不显著，且模型拟合优度较小，因而单一理性预期不能很好地刻画通胀预期对当期通胀率的影响，说明我国新凯恩斯菲利普斯曲线不具有纯粹理性预期的特征。

（二）基于混合学习预期的我国新凯恩斯菲利普斯曲线估计

本文设定的混合学习预期有两种：一种是理性预期与适应性学习预期的混合学习预期;一种是高阶滞后适应性预期与适应性学习预期的混合学习预期。估计过程与单一预期一致。

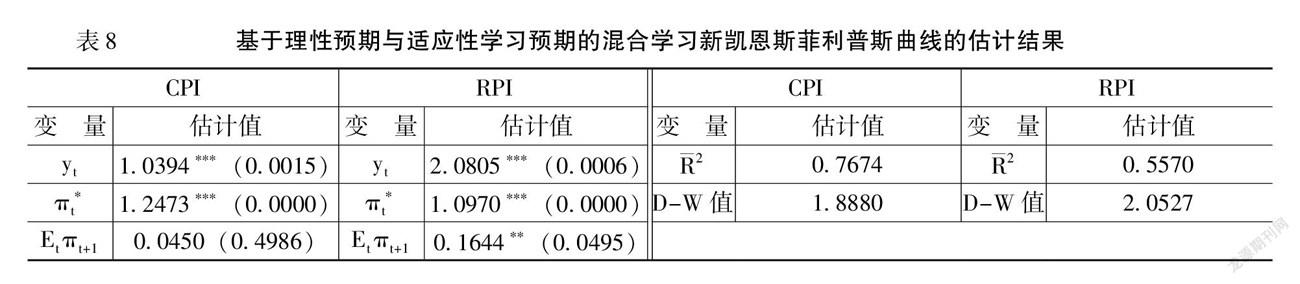
首先，对基于第一种混合学习预期的新凯恩斯菲利普斯曲线模型（9）进行估计，如表8所示。由表8可知，当以CPI为通胀率时，产出缺口与通胀率的权衡系数、适应性学习预期系数均在1%的水平下显著，但理性预期系数却并不显著。对比模型（9）与模型（7）的产出缺口与通胀率的权衡系数及適应性学习预期系数，发现二者的系数差别不大，模型（7）中的权衡系数和学习预期系数分别为1.1513和1.2373，模型（9）的权衡系数和学习预期系数分别为1.0394和1.2473，且均在1%水平下显著。这表明，理性预期的引入并不能有效改变新凯恩斯菲利普斯曲线模型（7）的预期特征，同时考虑到理性预期系数不显著，因此，我国新凯恩斯菲利普斯曲线不具有理性预期与适应性学习预期的混合学习预期特征，但具有适应性学习预期特征。当以RPI为通

胀率时，产出缺口和通胀率的权衡系数、适应性学习预期系数在1%的水平下显著，同时菲利普斯曲线模型（9）和模型（7）的产出缺口与通胀率的权衡系数及适应性学习预期系数估计值也差别不大且均在1%水平下显著，新凯恩斯菲利普斯曲线模型（7）中的权衡系数和学习预期系数分别为2.5315和1.0911，新凯恩斯菲利普斯曲线模型（9）的权衡系数和学习预期系数分别为2.0805和1.0970。尽管新凯恩斯菲利普斯曲线模型（9）的理性预期系数在5%的水平下显著，但其系数值（0.1644）相对于权衡系数和学习系数要小得多，理性预期对通胀率的影响依然不大，理性预期与适应性学习预期的混合学习预期特征仍不显著，但具有较强的适应性预期特征，这与以CPI为通胀率的结论是一致的。

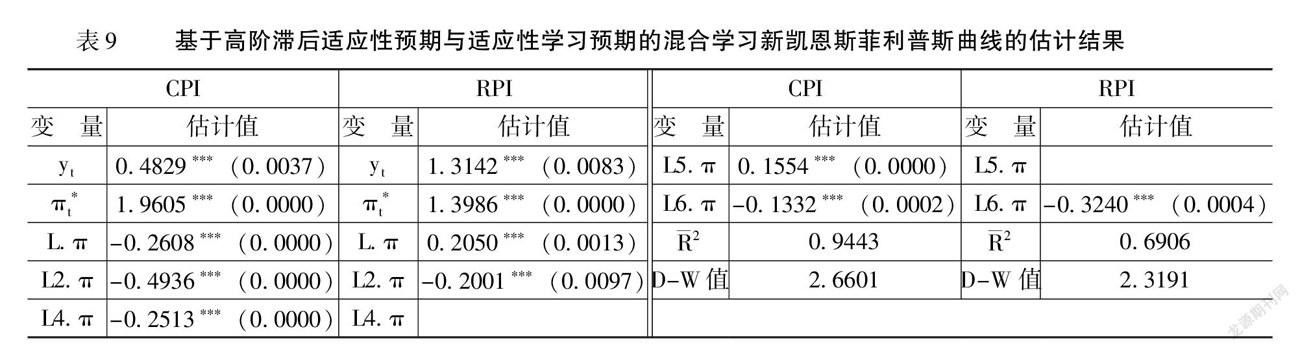
其次，对基于第二种混合学习预期的新凯恩斯菲利普斯曲线模型（10）进行估计，估计过程中，为稳健起见，依次加入通胀率的滞后项并删除不显著的滞后项。当以CPI为通胀率时，6阶以上滞后项系数的P值均显著大于10%，因而选择滞后1—6阶通胀率，其中滞后3阶通胀率系数的P值为0.5669，参数估计值不显著，因而删除重新估计，表9给出了最终估计结果。由表9可知，产出缺口与通胀率的权衡系数和适应性学习预期系数均在1%的水平下显著，且适应性学习预期对通胀率存在正向影响，这与新凯恩斯菲利普斯曲线模型（7）和模型（9）的结论一致。对比新凯恩斯菲利普斯曲线模型（10）和模型（7）的权衡系数和学习预期系数，可以发现权衡系数下降，由1.1513变为0.4829，而学习预期系数上升，由1.2373变为1.9605，这表明，适应性预期的引入增强了我国新凯恩斯菲利普斯曲线的学习预期特征。与基于高阶滞后适应性预期的新凯恩斯菲利普斯曲线模型（6）对比，适应性学习预期的引入显著提高了调整拟合优度，因而可以更好地刻画我国新凯恩斯菲利普斯曲线的预期特征。对于通胀率的高阶滞后项，1、2、4、5和6阶滞后项系数估计值均显著，而在五个滞后项的系数中，只有5阶滞后项的系数是正值，其他阶数滞后项的系数均为负值，其中2阶滞后项系数的绝对值最大，因而在高阶滞后预期中对通胀率的影响最大。进一步，五个滞后项的系数之和为-0.8876，系数之和的绝对值小于适应性学习系数，因而适应性学习预期特征要强于高阶滞后预期特征。这与前面的结论也一致，即相比于高阶滞后预期，适应性学习预期可以更好地反映我国的通胀预期形成机制。在基于混合预期的新凯恩斯菲利普斯曲线中，通胀率的滞后项反映了通胀惯性和货币政策的时滞性，但是在基于适应性学习预期的条件下，通胀率滞后项的系数之和却小于0，这意味着我国新凯恩斯菲利普斯曲线具有适应性预期与适应性学习预期的混合学习预期特征，同时适应性预期对通胀率的影响表现为逆向的通胀惯性。

当以RPI为通胀率时，6阶以上滞后项的系数P值均显著大于10%，因而选择滞后1—6阶通胀率，其中滞后3—5阶通胀率的系数估计值不显著，因而删除重新估计，表9给出了最终估计结果。由表9可知，产出缺口与通胀率的权衡系数、适应性学习预期系数均在1%的水平下显著，且适应性学习预期对通胀率存在正向影响，这与CPI为通胀率的结论一致，也与新凯恩斯菲利普斯曲线模型（7）和模型（9）的结论一致。对比新凯恩斯菲利普斯曲线模型（10）与模型（7）的权衡系数与学习预期系数发现权衡系数下降，由2.0805变为1.3142，而学习预期系数上升，由1.0970变为1.3986，这同样说明了适应性预期的引入增强了我国新凯恩斯菲利普斯曲线的学习预期特征。与新凯恩斯菲利普斯曲线模型（6）对比，适应性学习预期的引入同样显著提高了调整拟合优度。对于通胀率的高阶滞后项，1、2、6阶滞后项系数估计值均显著，而在三个滞后项的系数中，只有1阶滞后项的系数是正值，其他阶数滞后项的系数均为负值，三个滞后项的系数之和为-0.3191，系数之和的绝对值小于适应性学习系数，因而我国新凯恩斯菲利普斯曲线具有适应性预期与适应性学习预期的混合学习预期特征，但适应性学习预期特征要强于高阶滞后预期特征。通胀率滞后项的系数之和小于0，同样说明适应性预期对通胀率的影响表现为逆向的通胀惯性。这与以CPI为通胀率的结论一致。

虽然基于第二种混合学习预期可以较好地刻画出两种不同通胀率指标下的我国新凯恩斯菲利普斯曲线的形式，但是估计结果还是有所差异。以CPI为通胀率的新凯恩斯菲利普斯曲线模型（10）包含五阶滞后项，而以RPI为通胀率的菲利普斯曲线模型（10）则包含三阶滞后项。将新凯恩斯菲利普斯曲线中通胀率滞后项系数和的绝对值与适应性学习预期项的系数相比，则以CPI为通胀率的比值为0.5016，以RPI为通胀率的比值为0.2268，说明以RPI为通胀率的新凯恩斯菲利普斯曲线的适应性学习预期的特征更强，高阶滞后适应性预期对通胀率的影响相对较小。因而在不同通胀率指标下，通胀预期对新凯恩斯菲利普斯曲线影响程度不同，即采用不同的指标来

衡量通胀率，高阶滞后适应性预期和适应性学习预期的影响程度会不同，因此，货币当局在制定货币政策时，应首先明确关心通胀率指标，然后才能有的放矢地稳定公众通胀预期以及调整通胀惯性。而无论采用哪种通胀率指标，货币当局都应提高货币政策的信誉度、透明度和独立性，并适度减少货币政策的调整频率，这样既能够稳定公众通胀预期，又能够减少通胀惯性的逆向影响。

五、主要结论与政策建议

本文基于1991—2020年的季度数据，通过构建适应性学习预期的状态空间模型，采用卡尔曼滤波算法对我国学习型通胀预期进行了测度，并将适应性学习预期、高阶滞后适应性预期、理性预期及其混合预期分别代入新凯恩斯菲利普斯曲线进行经验研究，进而分析我国新凯恩斯菲利普斯曲线的混合学习预期特征。同时为使结论稳健，本文分别以消费者价格指数CPI和商品零售价格指数RPI为通胀率指标进行检验。结果表明：

第一，当显著性水平为10%时，公众基于适应性学习预期同时满足认知偏差均值为0、无偏性、强有效性以及序列不相关;当显著性水平为5%或1%时，公众基于适应性学习预期并不完全满足认知偏差均值为0、无偏性、强有效性。因此，我国适应性学习预期并非完全理性预期，而是一种近理性预期，具有近理性特征。

第二，我国新凯恩斯菲利普斯曲线具有高阶滞后适应性预期与适应性学习预期的混合学习预期特征，同时高阶滞后适应性预期对通胀率的影响表现为逆向的通胀惯性。

第三，适应性学习预期特征要强于高阶滞后适应性预期特征，即相比于高阶滞后适应性预期，适应性学习预期可以更好地反映我国通胀预期形成机制，但适应性学习预期相对于高阶滞后预期的强度受通胀率衡量指标的影响。

基于此，笔者提出如下政策建议：

第一，由于不同通脹率衡量指标所对应的新凯恩斯菲利普斯曲线的具体形式不同，具体表现为适应性学习预期对高阶滞后预期的相对强度不同，或者说适应性学习预期和高阶滞后预期对通胀率的影响程度不同，因而货币当局在制定政策时，应首先明确关心的是哪种通胀率指标可以更好地对我国新凯恩斯菲利普斯曲线进行刻画，这样才能保证货币政策有的放矢和有效性。

第二，从我国近年来货币政策的实践来看，宏观经济运行本身具有复杂多变的特征，加之近两年新冠肺炎疫情的冲击，经济发展受到严重挑战，使得公众难以形成稳定预期，而我国新凯恩斯菲利普斯曲线具有适应性学习预期和高阶滞后适应性预期的混合学习预期特征，既包含了学习特征，又包含了惯性特征，因此，货币政策调控应从两个方面完善：一方面，对于适应性学习预期，货币当局应注意对公众预期的引导，防止公众学习程度出现过高或过低;另一方面，对于高阶滞后适应性预期，货币当局应适度控制货币政策的调整频率。

第三，在适应性学习预期的引导上，货币当局应重视公众适应性预期的形成机制。虽然本文估计的适应性学习预期可以很好地刻画真实通胀率，但公众的学习机制是一个不断调整的过程，在这一调整过程中，央行沟通和货币政策工具实施至关重要。如果货币当局沟通边界有限造成所提供的信息不如私人信息准确，或者对主要实施的货币政策工具并没有给予足够的重视，则货币当局沟通反而会造成公众信息损失，其政策实施也会与公众的预期存在偏差。为引导适应性学习预期趋于理性预期，货币当局应该提高货币政策的透明度与可信度，提高与公众沟通的信息质量，确保公众从货币当局的沟通中得到的信息要大于通过其他方式所得到的信息，避免公众形成预期过程中的信息损失。同时货币当局应注重声誉和信用，保持货币政策工具实施的一致性和连贯性。，避免由于主要货币政策工具实施的转换导致货币政策出现动态不一致性。

参考文献：

[1] Lucas，R.E.Expectations and the Neutrality of Money [J].Journal of Economic Theory，1972，4（2）：103-124.

[2] Taylor，J.B.Aggregate Dynamics and Staggered Contracts [J].Journal of Political Economy，1980，88（1）：1-23.

[3] Evans，G.Expectations Stability and the Multiple Equilibria Problem in Liner Rational Expectations Models [J].Quarterly Journal of Economics，1985，100（4）：1217-1233.

[4] Cogley，T.，Sargent，T.J.The Conquest of US Inflation： Learning and Robustness to Model Uncertainty[J].Review of Economic Dynamics，2005，8（2）：528-563.

[5] Evans，G.W.，Honkapohja，S.Learning and Expectations in Macroeconomics[M].Princeton ：Princeton University Press，2001.

[6] Orphanides，A.，Williams，J.Imperfect Knowledge，Inflation Expectations，and Monetary Policy[R].NBER Working Paper No.9884，2004.

[7] Milani，F.Adaptive Learning and Inflation Persistence[R].University of California-Irvine Working Paper No.50607，2005.

[8] Milani，F.Expectations，Learning and Macroeconomic Persistence[R].University of California-Irvine Working Paper No.50608，2005.

[9] Zhang，C.，Kim，O.D.H.The New Keynesian Phillips Curve： From Sticky Inflation to Sticky Prices[J].Journal of Money，Credit and Banking，2008，40（4）：667-699.

[10] Sousa，R.，Yetman，J.Inflation Expectations and Monetary Policy[R].BIS Papers，2016.

[11] Coibion，O.，Gordnichenko，Y.，Weber，M.Monetary Policy Communications and Their Effects on Household Inflation Expectations[R].NBER Working Paper No.25482，2019.

[12] 黎文靖，郑曼妮.通货膨胀预期、企业成长性与企业投资[J].统计研究，2016，（5）：34-42

[13] 何启志，姚梦雨.中国通胀预期测度及时变系数的菲利普斯曲线[J].管理世界，2017，（5）：66-78.

[14] 姚余栋，谭海鸣.中国金融市场通胀预期——基于利率期限结构的量度[J].金融研究，2011，（6）：61-70.

[15] 卞志村，高潔超.适应性学习、宏观经济预期与中国最优货币政策[J].经济研究，2014，（4）：32-46.

[16] 李昊，王少平.我国通货膨胀预期和通货膨胀粘性[J].统计研究，2011，（1）： 43-48.

[17] 卞志村，胡恒强.粘性价格、粘性信息与中国菲利普斯曲线[J].世界经济，2016，（4）：22-43.

[18] 何启志，范从来.学习型预期与中国扩展的新菲利普斯曲线的研究[J].金融研究，2014，（9）：34-52.

[19] Cuckierman，A.，Meltzer，A.H.A Theory of Ambiguity，Credibility and Inflation Under Discretion and Asymmetric Information[J].Econometrica，1986，54（5）：1028-1099.

[20] Mehra，Y.P.Survey Measures of Expected Inflation： Revisiting the Issues of Predictive Content and Rationality[J].Economic Quarterly，2002，88（3）： 17-36.

[21] Gali，J.，Gertler，M.Inflation Dynamics： A Structural Econometric Analysis[J].Journal of Monetary Economics，1999，44（2）： 195-222.

[22] 杨继生.通胀预期、流动性过剩与中国通货膨胀的动态性质[J].经济研究，2009，（1）：106-117.

An empirical Study on the New Keynesian Phillips Curve in China Based on Mixed Learning Expectation

DaiXiaobing  Guo Kai，Li Zhichao

Abstract：Based on quarterly data from 1991 to 2020，this paper uses the Kalman filter algorithm to measure China's learning inflation expectations by constructing an adaptive learning inflation expectations state space model.And the adaptive learning expectations，high-order lagging adaptive expectations，rational expectations and their mixed expectations are respectively substituted into the New Keynes Phillips Curve for empirical analysis，so as to analyze the characteristics of mixed learning expectations of China's New Keynes Phillips Curve.Empirical research shows that： （1） China's adaptive learning inflation expectations are not completely rational expectations，but a near-rational expectation with near-rational characteristics; （2） China's New Keynesian Phillips curve has the characteristics of mixed learning expectation of high-order lag adaptive expectation and adaptive learning expectation.At the same time，the impact of high-order lag expectation on inflation rate is reverse inflation inertia;（3） The characteristics of adaptive learning expectation are stronger than high-order lag expectation，that is，compared with high-order lag expectation，adaptive learning expectation can better reflect the formation mechanism of inflation expectation in China.However，the strength of adaptive learning expectation relative to high-order lag expectation is affected by the measurement index of inflation rate.

Key words：Adaptive Learning Expectation;New Keynesian Phillips Curve;Hybrid Expectation; Kalman Filter

（責任编辑：刘 艳）

收稿日期：2021-12-03

基金项目：教育部人文社会科学规划基金项目“金融稳定、前瞻性扩展货币政策规则与不确定性：基于LRE模型的实证分析与检验研究”（18YJA790027）;辽宁省教育厅高等学校基本科研项目“数字普惠金融与辽宁绿色全要素生产率”（LJKR0432）

作者简介：戴晓兵（1986-），女，辽宁辽阳人，讲师，博士，主要从事金融市场研究。E-mail： daixiaobing_800@sina.com

李志超（1995-），男，辽宁铁岭人，硕士研究生，主要从事货币政策研究。E-mail：252182806@qq.com]