基于DNN 神经网络的PMSM 控制策略研究①

黄国凯

(福建船政交通职业学院,福建 福州 350007)

0 引 言

随着低碳时代的到来,电动汽车作为一种绿色环保的新能源出行方式逐渐受到人们的重视。PMSM(Permanent Magnet Synchronous Motor),即永磁同步电机系统作为电动汽车内部对电能进行机械能转化的重要装置,是电动汽车搭载最为普遍的电机种类之一[1-2]。传统的PMSM 控制方式无法有效抑制电磁转矩的波动,而DNN(Deep Neural Network)神经网络作为一种能够模仿人类大脑运行方式对信息进行分类以及预测的计算机算法,可以通过自身独特的架构特点对PMSM 系统进行优化,DNN 神经网络目前广泛应用于诸如肿瘤细胞识别、语音助手分析等多个领域,以良好的分类和预测效果著称[3-4]。将DNN 神经网络应用到PMSM 系统中可以有效抑制电磁转矩的波动,使得电动汽车在正常行驶和突然转向的过程中保持车身稳定,提升用户的驾驶体验,为驾驶安全提供保障。

1 基于DNN 神经网络的PMSM 控制策略设计

1.1 DNN 神经网络技术分析

DNN 神经网络是以BP(Back Propagation)神经网络为基础发展而来的神经网络技术。传统的BP神经网络是由单一的输入层、隐藏层、输出层组成的较为简单的神经结构,但是DNN 神经网络内部包含多个隐藏层,是一种具有深层感知能力的神经网络技术,其内部多个输入层、隐藏层与输出层保持两两连接,并了利用梯度下降的方法进行反向传播,具体架构如图1所示。

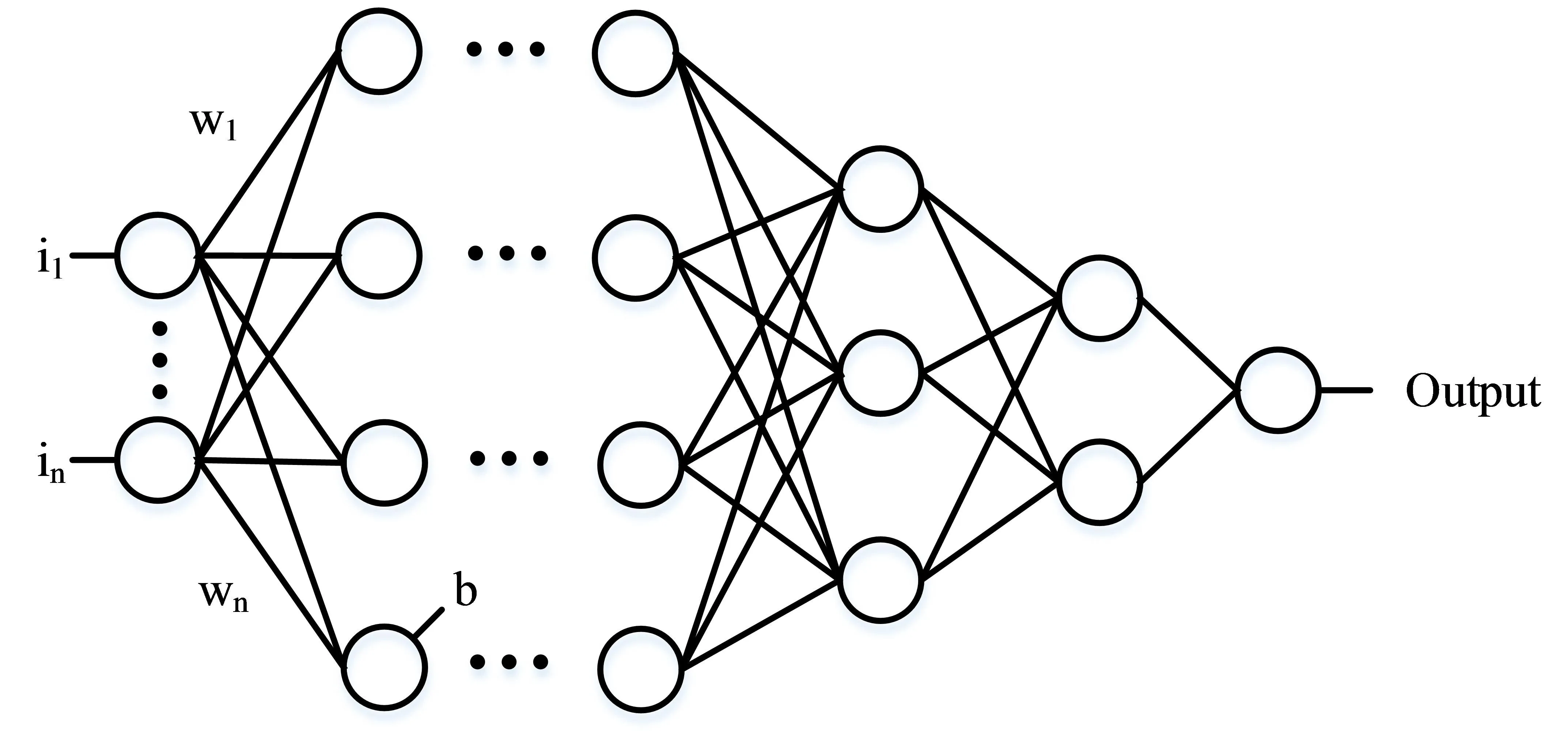
图1 DNN 神经网络架构

图1中i1到in为输入层的输入值,输入值在经过神经元的赋权后还需添加神经元的偏置值,如公式(1)所示:

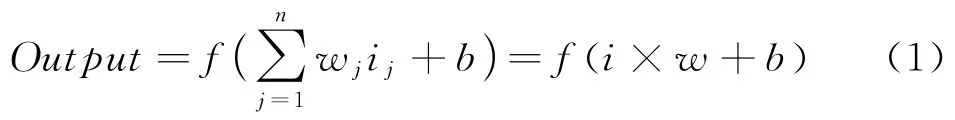
式(1)中f x（ ） 表示激活函数,wj表示神经元为每个输入值赋予的权重,b表示神经元带有的偏置值。神经元的激活函数种类有很多,其中最终输出值均值大于0的函数不适合用于数据拟合之中,因此尽量选用输出值均值为0的函数作为激活函数,本次研究依照此原则选用tanh函数作为激活函数,其表达式如公式(2):

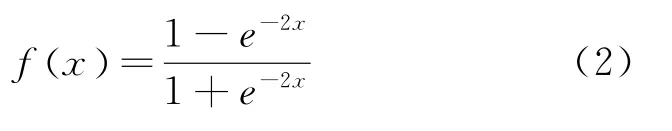
1.2 基于DNN神经网络的PMSM 控制策略实现方法

为了对控制系统进行一定程度上的简化,以坐标变换的方式将电机中三相电压与三相电流转换到d-q坐标系的电压与电流之中,在d-q坐标系中,PMSM 系统的数学表达如公式(3)所示:

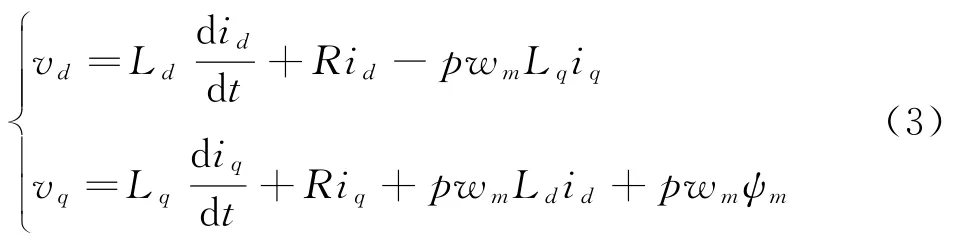
式(3)中vd表示d轴的电压,vq表示q轴的电压,id与iq分别表示两轴上的电流,Ld与Lq分别表示两轴上的电感,ψm表示永磁体产生的磁链,R表示定子绕组电阻,wm表示转速,pn表示磁极的对数。从公式构成可以看出,可见电机在d-q两轴上的电压实际上是由电流决定的,在此基础上电机输出转矩Te可以表示为式(4):

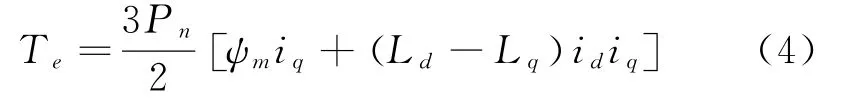
可以看出输出转矩也与电流相关,控制电机的本质在于电流的控制,从两轴电流的不同组合中可以产生一个最优组合使得电机的输出转矩达到最高。在利用DNN 神经网络进行PMSM 控制的过程中,DNN 神经网络的输入值便是三相电流以及电机运行时的角速度,在经过DNN 神经网络激活函数的数据拟合之后,将得到的转矩指令与DNN输出值一同输入转矩控制器之中,转矩控制器根据接收到的指令和DNN 神经网络的输出值对电流进行优化和调整,一旦得到最优化的电流组合,那么便可由电流控制器通过数学运算输出相对应的电压组合。得出的电压组合在转换为实际的三相电压后可以进一步通过三相逆变器得到三相交流电信号,最终达到控制电机的输出转矩的效果。

2 基于DNN 神经网络的PMSM 控制策略效果分析

2.1 应用在PMSM控制中的DNN神经网络性能分析

本次研究从应用在PMSM 控制中的DNN 神经网络的性能与PMSM 控制策略应用效果两方面进行控制效果分析。在DNN 神经网络的性能分析部分,本次研究将应用在PMSN 中的BP神经网络、ELM 神经网 络、LSTM 神经网络3 种 神 经 网络算法与DNN 神经网络算法进行预测误差平均值对比。设定小型样本集样本数量为50个,大型样本集样本数量为150个,具体结果如图2所示。

图2 预测误差平均值对比图

如图2所示,当样本数为50个时,DNN 的预测误差平均值最低,为0.74N·m,预测误差平均值最大的为BP神经算法,达到了1.83N·m,位于两者之间的分别为ELM 神经算法以及LSTM 神经算法,预测误差平均值分别为1.68N·m 与1.39N·m,从对比中可以看出DNN神经算法的预测误差最小,性能最为优异;当样本数为150个时,DNN 的预测误差平均值同样为最低,为0.58N·m,较样本数为50个时预测误差有所下降,预测误差平均值最大的仍为BP神经算法,达到了1.98N·m,位于两者之间的分别为ELM 神经算法以及LSTM 神经算法,预测误差平均值分别为1.91N·m 与1.44N·m,从对比中可以看出DNN 神经算法的预测误差最小,且随着样本量增加误差呈现逐渐减小的趋势,性能最为优异。

2.2 基于DNN 神经网络的PMSM 控制策略应用效果分析

在基于DNN神经网络的PMSM 控制策略应用效果分析部分,本次研究将应用了DNN神经网络的PMSM 系统与基于传统PI算法的PMSM 系统进行控制效果对比,对比主要从正常转矩状态与负载突变状态2个方面进行对比分析,具体如图3所示。

图3中,在正常转矩状态下,基于PI算法的控制系统电磁转矩折线纵向波动较大且较频繁,范围约介于2.00N·m 到2.50N·m 之间,可以看出转矩并未得到有效的抑制。而基于DNN 神经网络的控制系统转矩折线纵向波动较小,大约介于2.20N·m 与2.30N·m 之间,对转矩起到了有效的抑制效果;在负载突变状态下,PI系统的控制折线同样产生了较强的波动,这种波动在2.02s后较为频繁,在2.02s前的突变过程中产生较少。而DNN 系统的控制折线在突变过程中与突变后波动都相对较少,且波动范围较窄,突变后折线波动约介于2.52N·m 到2.63N·m 之间。可见无论正常转矩状态还是转矩突变状态,DNN 系统的控制效果都更好,系统更加稳定。

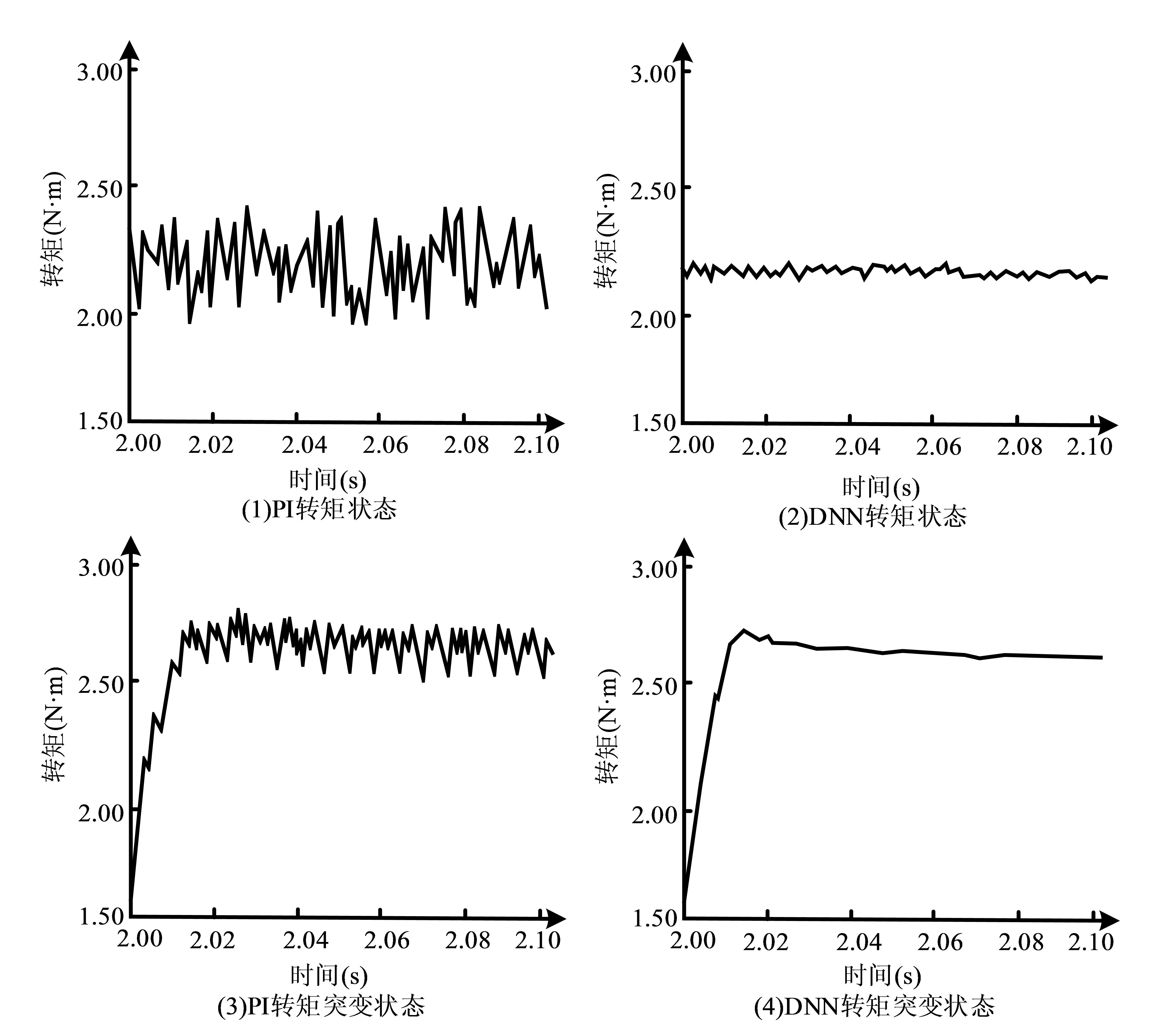
图3 基于DNN 神经网络的PMSM 控制策略应用效果分析

3 结 语

PMSM 系统的控制效果与电动汽车安全性能息息相关,为增强PMSM 系统控制效果,本次研究从DNN 神经网络的结构特点出发,将DNN 神经网络应用到PMSM 系统控制的电流控制之中,达到通过优化电流组合来控制转矩输出的效果。结果显示DNN 神经网络在50个样本与150个样本2种状态下的预测误差平均值分别为0.74N·m与0.58N·m,相较其他算法而言具有性能优越性。将DNN 神经网络应用到PMSM 系统之中,输出的转矩在正常与突变状态下的波动范围都更小,分别位于2.00N·m 到2.50N·m 之间与2.52N·m 到2.63N·m 之间,可见基于DNN 神经网络的PMSM 控制系统能够有效减小转矩波动,控制效果更好,更能保证电动汽车的安全性。