基于滑模速度控制器的PMSM 二阶滑模直接控制①

胡 霞, 李帅帅

(安徽理工大学,安徽 淮南 232001)

0 引 言

永磁同步电机(permanent magnet synchronous motor,PMSM )的响应速度比较快、调速范围广、其转矩惯量比高、并且具有高效率和高功率因数的特点。因此在新能源汽车等中小功率电气传动领域应用十分广泛。当前对于PMSM常用的控制策略可以分为矢量控制(field -oriented control,FOC)和直接转矩控制(direct torque control,DTC)。矢量控制就是对变流器的电流、电压进行clack和park变换再进行控制,其原理就是将此时的电机等效为一个直流电机,然后再对其控制。而DTC则是对电机中的转矩与磁链进行直接控制,不同于FOC 中的解耦方法,控制结构简单,动态响应快,控制效果突出,其控制方法要优于FOC。然而在传统的DTC中还是出现转矩脉动与磁链脉动比较大,启动转速超调等问题。

为解决上述问题提出了一种基于滑模速度控制器的PMSM 二阶滑模直接控制,引入了滑模速度控制器和二阶滑模控制器,采用空间电压矢量脉冲调制(SVPWM )方法。并进行了仿真实验,表明此方案对上诉存在的问题有了很大改善。

1 永磁同步电机的数学模型

本文研究对象为表贴式永磁同步电机(Surface Permanent Magnet Synchronou Motor,SVPWM ),并假设电机处在理想状态。处于三相静止坐标系下的PMSM 数学模型通过clack 和park变换的到d-q 坐标系。

式(1)中:ud,uq,id,Ld,iq,Lq分别为d-q 坐标轴上面的电压、电流和电感;wm,we分别为电机的机械角速度和电角速度;pn为极对数;J为转动惯量;TL为负载转矩

2 滑模速度控制器的设计

使用电机为SPMSM ,且采用id=0控制。此时的(1)式可以为下数学模型。

对式(9)进行积分,从而得到q轴电流的参考电流。

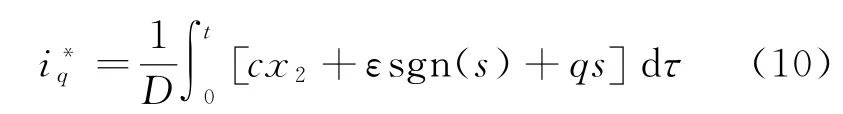
在式(10)中因为积分项的存在,控制器可以有效的减弱抖振现象以及减少控制系统的稳态误差。

而滑模达到条件容易证明

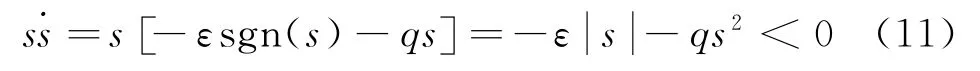
则表明在控制器下的系统是渐近稳定的。

3 磁链控制器和直接转矩控制器设计

表贴式三相PMSM 在同步旋转系d-q下的矢量模型可以表示为式(12):

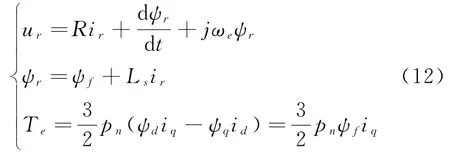
当定子磁链矢量方向与d轴方向一致时,ψd=ψr,此时磁链的幅值可以表示为式(13):

首先为了求磁链控制器的方程,将磁链的滑模函数定义为式(14):

在设计二阶滑模控制时,利用super-twisting算法,此时在滑模控制下磁链控制器的表达式为式(15):

式(15)中:Kp,Ki＞0为控制系统的设计参数。

当定子磁链ψf的幅值不变为一常数时,电磁转矩Te微分方程为式(16):

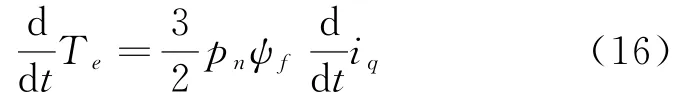
同样为求转矩控制器方程,将转矩的滑模面函数定义为式(17):

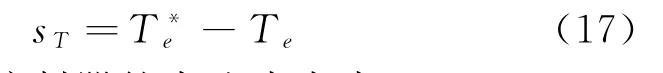
同理,转矩控制器的表达式为式(18):

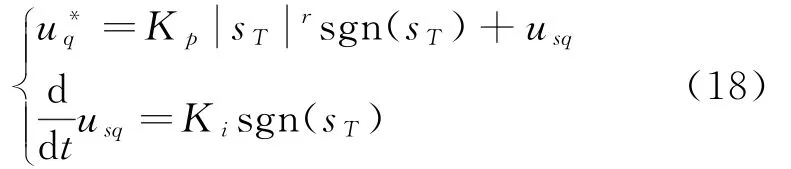
设计控制器中参数r=0.5,Kp =100,Ki =1

4 模型搭建仿真及分析结果

仿真电机模型选用SPMSM :极对数PN =4,定子电感值和电阻值分别为Ls =8.5m H,R =1.5Ω ,磁链Ψf=0.175wb,转动惯量J=0.0008kg·m2。参考转速设为600r/min,设置电机在初始时刻的负载转矩为TL =0N·m ,在t=0.2s时TL=1.5N·m。

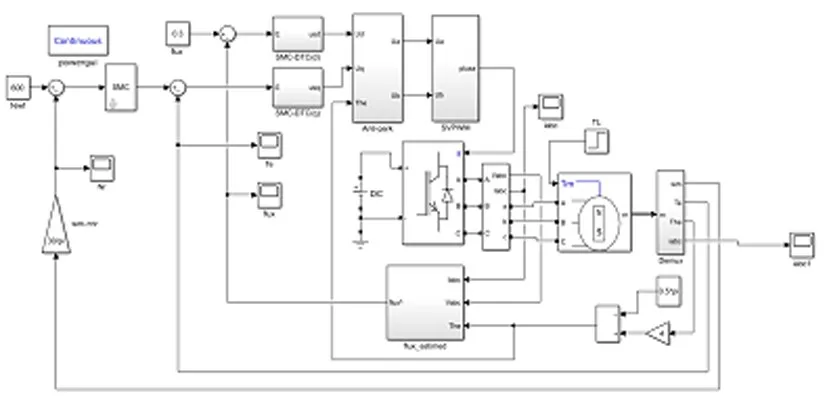
图1 基于滑模控制的DTC仿真模型搭建

仿真结果:

通过图2可以看出传统的直接转矩在启动时存在着超调现象,超调量接近了15%,而且在负载转矩在0.2S时由0 N·m 升为1.5 N·m 时,系统的调节时间较长。而改进后的直接转矩在超调问题上得到了很大的改善,此时的超调量接近5%,而系统在转矩增大后的调节时间也得到了改善。

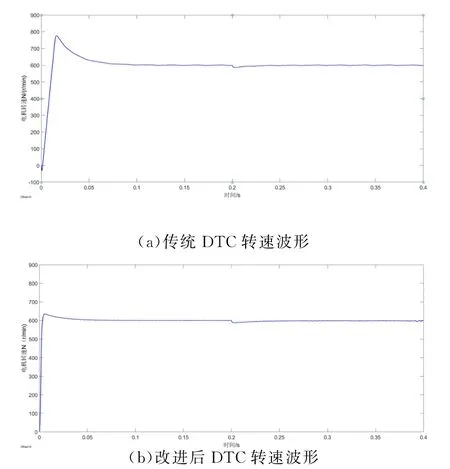
图2 系统转速仿真图

由图3可以明显看出传统的直接转矩在增加负载转矩前后,电磁转矩的波动都比较大。

图3 系统电磁转矩仿真图

而改进后的直接转矩在增加负载前后都较为稳定且波动明显减小,有效的降低转矩脉动,并且可以迅速达到稳定,增强了控制系统的精确度与系统整体的稳定。

由图4可看出,传统DTC系统的磁链反应速度较快,但波动较大为,磁链脉动为0.02Wb。而改进后DTC系统磁链虽然在反应速度上慢了约0.01s,但是波动范围明显减小,磁链脉动大约减少了0.01Wb。

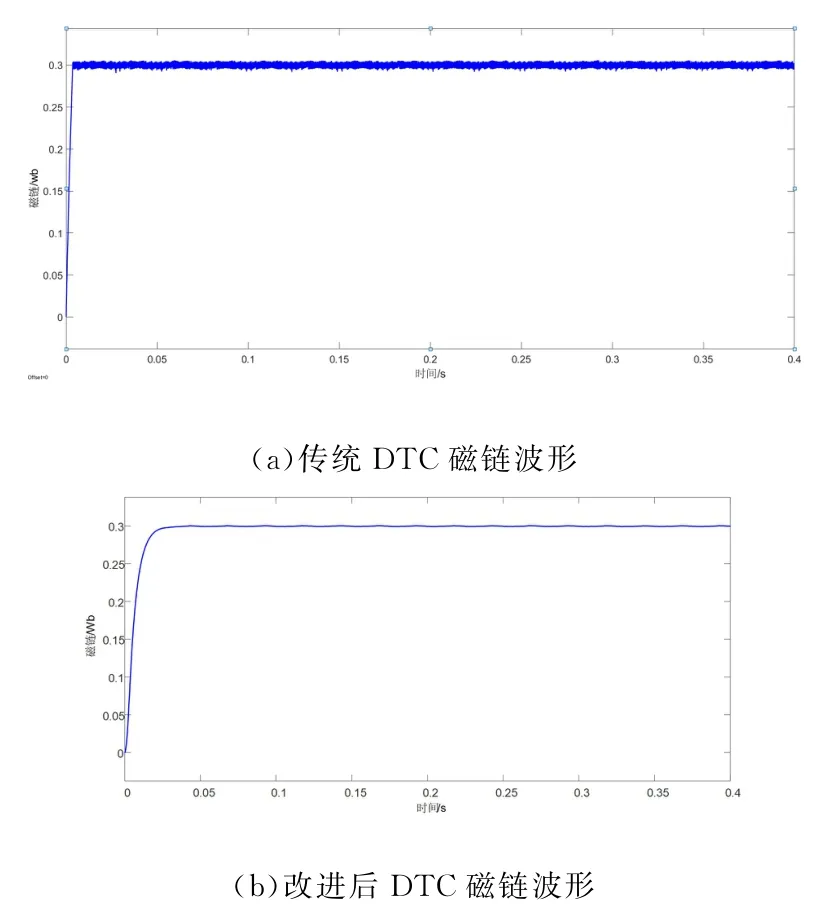
图4 系统磁链波形仿真图

5 结 语

实验表明:改进后的DTC 有效优化了系统中存在的问题,降低了控制过程中转速超调、转矩和磁链的脉动。然而在改进后的DTC 在启动开始时,电机仍然存在较小的超调量。对于此问题有待进行进一步的优化,使得超调量有所降低。