基于外增湿的燃料电池空气系统湿度控制策略研究①

高 特, 杨彦博

(同济大学汽车学院,上海 201804)

0 引 言

质子交换膜燃料电池(Proton exchange membrane fuel cell,PEMFC)被认为是最适合于燃料电池汽车的动力源[1],其辅助系统包括氢气系统、空气系统、水热系统和电控系统。其中,空气系统负责向电堆输出一定流量、压力、温度和湿度的空气。目前,对于空气系统流量和压力控制策略的研究已经相对成熟[2],空气温度的变化也较为线性,调控起来较为简单。而对于空气湿度来说,实际涉及到电堆内部水管理问题,其控制相关的研究较少且方向分散。一部分原因在于燃料电池系统中存在三种增湿方案,自增湿、内增湿和外增湿方案[3]。其中,自增湿和内增湿方案的结构较为复杂,技术难度较高,实际中大多采用外增湿方案,但外增湿方案的加湿器并不具备独立调控湿度的能力。另一部分原因在于,空气湿度受影响因素较多,其控制精度较难保证[4,5],且电堆入口处的湿度传感器由于处于高温高湿环境,反馈精度较差,响应速度也较慢[6]。

针对现有外增湿空气系统无法主动调控空气湿度、湿度影响因素多等问题,首先设计实验对系统模型中的膜加湿器模型进行验证,来保证湿度模型的准确性,然后在系统中空气流量、压力和温度调控稳定的基础上,通过模型研究对比具有不同比例阀(用于调节湿度)位置的空气系统拓扑结构,选出最优方案,并结合自抗扰控制原理设计湿度闭环控制器,代入模型中进行仿真验证。

1 外增湿空气系统

采用外增湿方式的空气系统结构如图1所示。

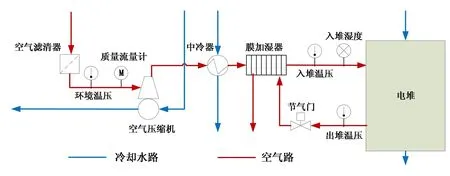
图1 外增湿空气系统结构示意图

1.1 膜加湿器模型

目前采用较多的外增湿装置是膜加湿器,其结构如图2 所示,分为干侧、湿侧以及膜三个部分。采用Pukrushpan等[7]的膜加湿器模型。

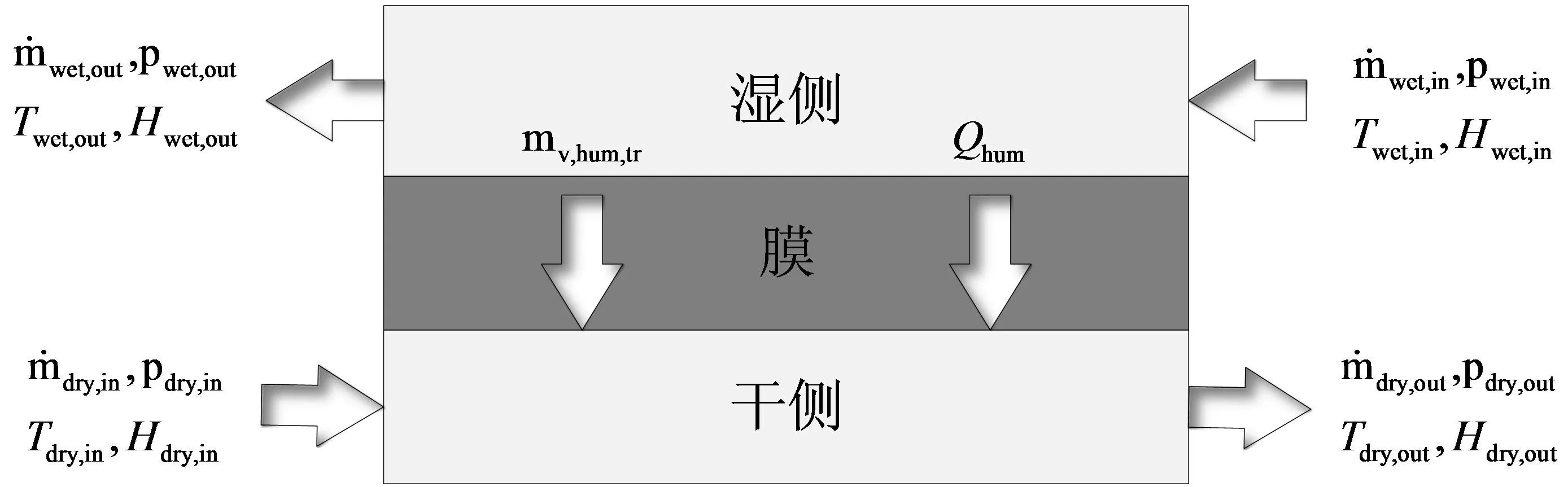
图2 膜加湿器结构示意图

膜加湿器模型不仅涉及到复杂的传热和传质过程,其精度直接影响电堆内部的水含量状态和自身的加湿表现。在实际系统中,中冷器出口的空气与电堆内部的温度相似,而电堆出口的湿废气会进入膜加湿器湿侧用于给干侧空气进行加湿,所以膜加湿器的加湿效果主要受干湿两侧含湿量和压差的影响。设计一组实验来验证膜加湿器模型的精度,变量为湿侧入口气体压力,其余条件不变。由于实验中所利用的气体均为干空气,经过调温、加湿后通入膜加湿器内的干湿侧,在流量不变的情况下,改变湿侧入口压力实则同时改变了进入湿侧气体的含湿量和压力,所以该组实验可以证明模型的精确性。设定模型输入非变量如表1所示,湿空气的含湿量可参考文献[8]用露点温度表示:

表1 膜加湿器模型输入非变量

式中,td为露点温度,单位℃;t为湿空气温度,单位℃;H为相对湿度,单位%。实验与仿真结果如图3所示,可以看出模型与实验的结果趋势基本一致。

图3 膜加湿器模型仿真与实验对比

1.2 空气系统模型

空气系统容易受到外部环境特性的影响,所使用的空气系统模型考虑了环境特性对空气压缩机的影响,可表示为:

式(2)中,̇m,p,T,H为入堆空气流量、压力、温度和湿度;x1～x10表示系统输入量。空气系统与流量压力控制器Simulink模型如图4所示。

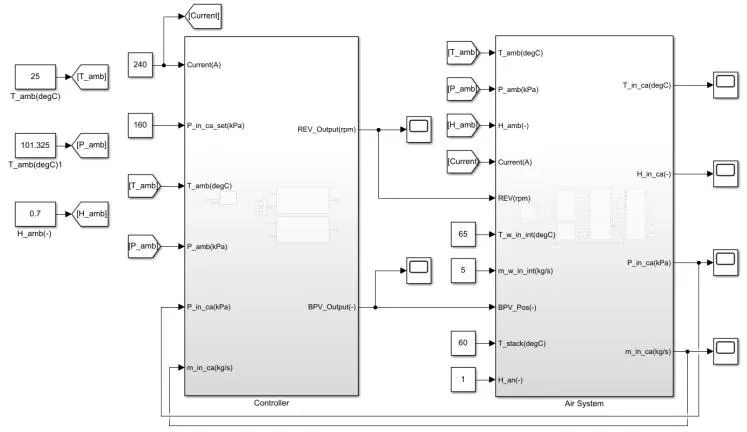
图4 空气系统与流量压力控制器Simulink模型

2 系统结构改进

在系统中存在流量压力控制器对空气压缩机和节气门进行调控,且中冷水流量调至最大时,最常见的空气湿度可控结构为在系统中添加比例阀,来改变膜加湿器干湿侧气体状态或实现部分气体的加湿[9]。此类方法简单且成本小,但比例阀所处的位置不同会使得可控范围的大小以及对系统稳定性的影响不同。

根据比例阀位置的不同,可分为带有调压阀、节流阀和泄流阀的三种空气系统结构方案(图5-图7所示)。以下分别对三种方案进行详细介绍,并结合模型得出其可控范围大小,对比分析最优方案。

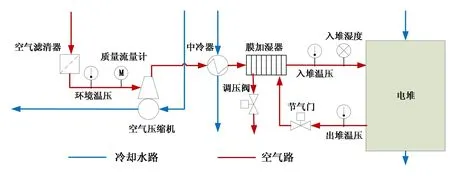
图5 带有调压阀的空气系统结构示意图

图7 带有泄流阀的空气系统示意图

2.1 带有调压阀的空气系统

如图5所示,若在膜加湿器湿侧附近添加比例阀,可与节气门一起配合来调控湿侧容腔内的压力,进而改变湿侧向干侧的水传递效率,一定程度上能实现对干侧空气湿度的调控,该位置比例阀可称为调压阀。

由于本文中节气门位于膜加湿器湿侧前端管路中,所以可在后端管路中添加调压阀。初步分析,当调压阀全开时,干侧空气湿度为正常输出值;当调压阀开到一定程度、节气门全开时,调压阀充当背压阀,此时湿侧容腔内的压力达到最高,水传递效率升高,干侧空气湿度达到最大。

调压阀由于处于系统最末端,对于电堆前端的零部件影响较小,仅对节气门的调控产生一定影响,系统稳定性较高。

2.2 带有节流阀的空气系统

如图6所示,若在膜加湿器干侧添加旁路绕过膜加湿器,干燥空气在进入膜加湿器前会进行分流,一部分通过膜加湿器加湿,另一部分绕过膜加湿器不进行加湿,随后在电堆入口处混合,此时可在旁路添加一个比例阀来控制旁通的空气流量,从而调控混合后的气体含湿量,该位置比例阀可称为节流阀。

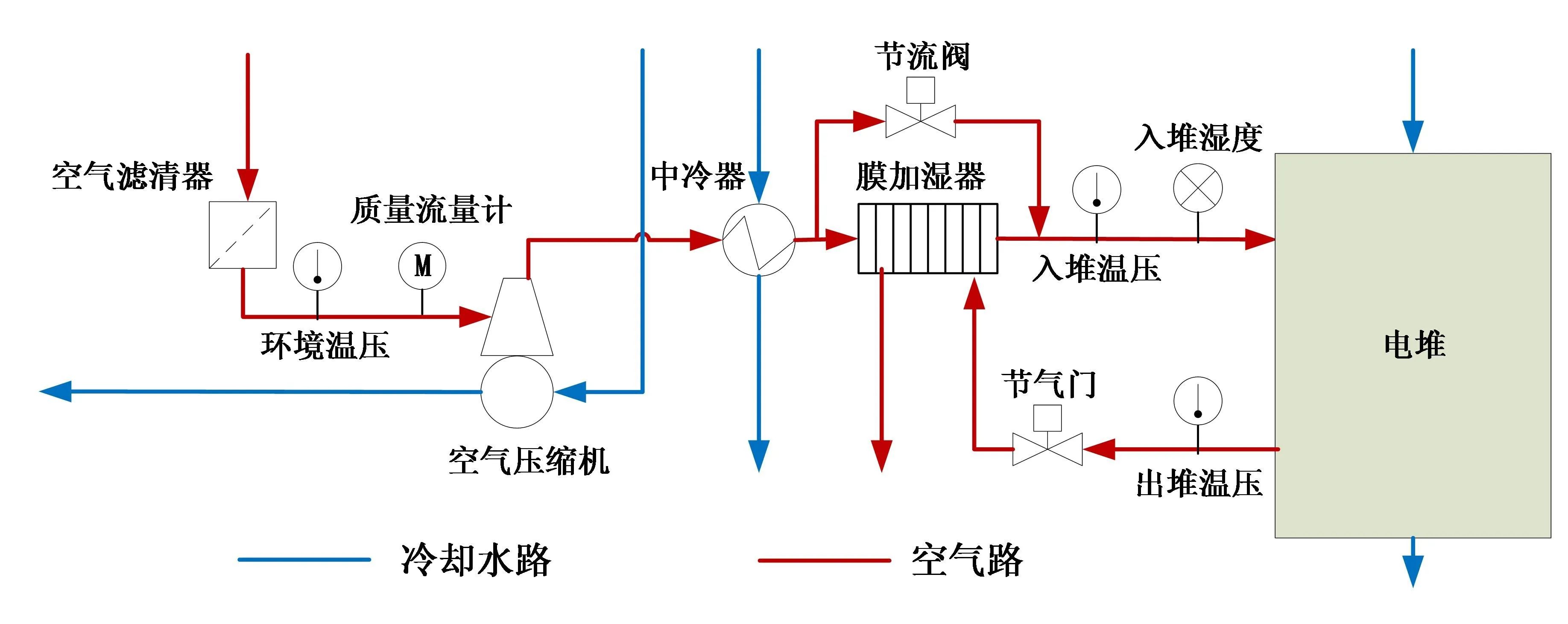
图6 带有节流阀的空气系统结构示意图

初步分析,当节流阀全闭时,电堆入口处的含湿量为正常输出值;当节流阀全开时,旁通空气流量达到最大,若假设此时分流后的两路压阻相等,则空气含湿量应近似等于节流阀全闭时的一半,混合后电堆入口处的含湿量达到最低。

此结构中节流阀靠近电堆入口,且一般情况下分流后的两路流阻不同,混合后的气体压力等参数会出现一定变化,从而导致入口处其余参数的波动,降低系统稳定性和其他执行器的控制精度。

2.3 带有泄流阀的空气系统

若将图6结构中的旁路和节流阀添加至膜加湿器湿侧,其可控范围理论上与图6结构相似。但由于膜加湿器的水传递过程是跨膜运输,膜的水传递效率会受到干湿侧的相对湿度影响,当降低湿侧的相对湿度时,膜的水传递效率降低,干侧将得到更少的水。相比于图6中的结构,其可控范围会更大。此外,改变湿侧气体状态并不会直接对干侧造成影响,而是经由膜的状态影响到干侧,其调节过程虽具有一定迟滞性,但也提高了控制容错率和抗噪声干扰能力,该结构将更为稳定可靠。

但此方案还可以进行一定改进,改进后的结构如图7所示,将湿侧的旁路直接连通大气,比例阀起到泄流的作用,此时的可控范围将更大,同时也兼具了较高的系统稳定性,该位置的比例阀可称为泄流阀。

初步分析,当泄流阀关闭时,干侧空气湿度为正常输出值;当泄流阀开到一定程度、节气门全开时,理论上此时几乎没有水蒸气进入膜加湿器湿侧,膜加湿器将不会对空气进行加湿,甚至可能造成膜向干侧吸水,此时干侧空气湿度降至最低。

此方案的优点为可控范围大,实现起来更为简单,但也存在一些问题。一方面由于泄流阀位于系统最末端,改变其开度会对背压产生一定影响,需要对节气门的控制精度提出更高要求。另一方面,湿度变化由湿侧响应到干侧的速度较慢,但也可以起到一定缓冲作用,从而避免误控或噪声干扰。综合来看,该系统稳定性较高,可控范围较大。

2.4 对比分析

基于以上分析,结合表2所示系统输入条件下的模型仿真结果,可总结出三种改进方案调节性能如表3所示。其中,比例阀的规格均与节气门相同。

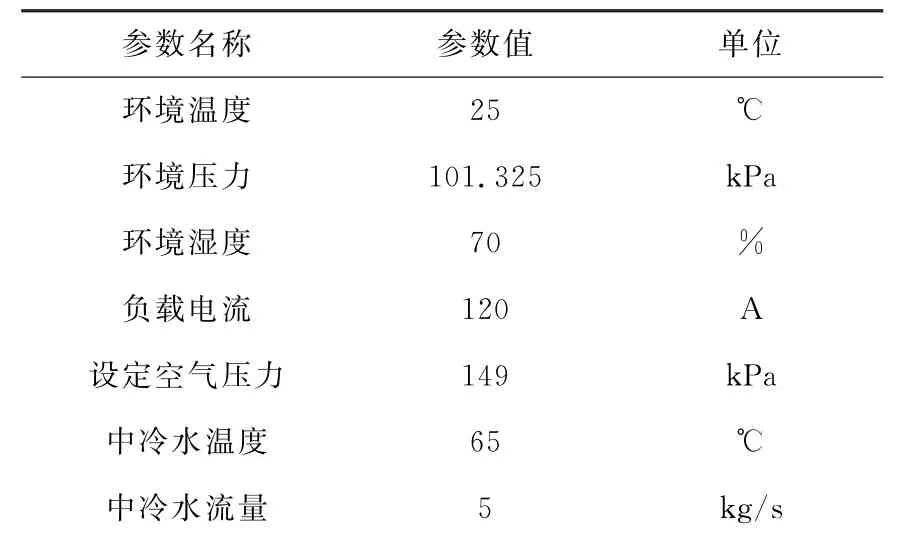
表2 系统输入量

表3 三种改进方案对比结果

电堆温度 60 ℃阳极湿度 100 %

可以看出,三种方案露点温度调节范围大小对比后的结果为:调压阀＜节流阀＜泄流阀,其中带有调压阀的改进方案可以在原基础上升高空气湿度,而其他两种方案则为降低空气湿度;系统稳定性对比后的结果为:节流阀＜调压阀=泄流阀。综合来看,采用泄流阀的系统结构可控范围最大,同时系统稳定性较高。选用此改进方案,则需要选用更高加湿性能的膜加湿器以适应最干燥的环境,来实现尽可能大的控制区间。

3 湿度控制策略

选取带有泄流阀的空气系统拓扑结构(如图7所示)作为研究对象,在系统中空气流量、压力和温度均调控稳定的情况下,结合自抗扰控制原理设计空气湿度控制器,并在模型中进行仿真验证。

3.1 自抗扰控制原理

自抗扰控制(Active disturbance rejection control,ARDC)结构示意图如图8所示。自抗扰控制由PID 控制发展而来,是一种可以解决复杂不确定性系统的有效控制方法,结构主要分为三个部分:跟踪微分器TD,扩张状态观测器ESO 和非线性状态误差反馈NLSEF。

图8 一阶自抗扰控制结构示意图

对于一阶系统来说,跟踪微分器TD 的作用是合理提取输入的微分信号,使其能够准确快速地跟踪到给定信号,用于解决不连续或带有随机噪声的离散信号和出现较大误差后的过渡缓冲。跟踪微分信号v1由以下公式求取:

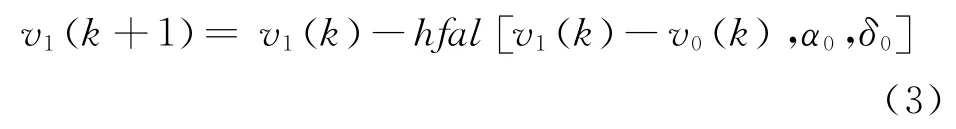
式(3)中,v1为跟踪信号,v0为设定信号,h为采样时间,k为采样序列。

状态观测器能够借助已有的输入变量和输出变量来估计出系统中的状态变量。而扩张状态观测器ESO 则可将控制信号的扰动作用扩张成新的状态变量,从而通过特殊的反馈机制观测被扩张的干扰信号。状态变量z1和被扩张的干扰变量z2的求取公式如下:

式(4)-(6)中,u为控制变量,y为输出变量,b为系统增益值;β01和β02为误差修正增益值,一般取1/h和1/3h2。

非线性状态误差反馈NLSEF 的作用为根据跟踪微分器TD 得出的跟踪信号与扩张状态观测器ESO 观测到的状态变量进行控制和扰动补偿,可表示如下:

式(7),(8)中,β为反馈过程中的比例放大系数。

下面介绍非线性函数,常见的有fsg(x,α,δ),fst(x,α,δ),fal(x,α,δ)和fhan(x1,x2,α,δ)函数[10]。其中,fal函数是上述TD,ESO和NLSEF三个板块的核心成分,其对于噪声具有很好的滤波作用。

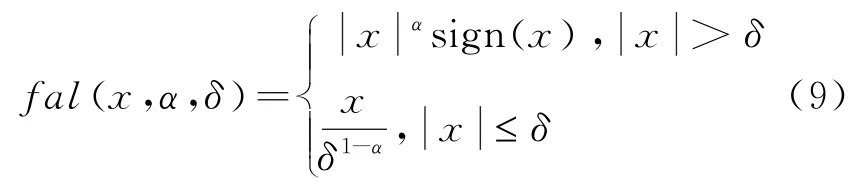
式(9)中,α为速度因子,一般取0到1;δ为滤波常数,一般取5h≤δ≤10h;sign函数为符号函数。

3.2 膜加湿器系统分析

选定泄流阀作为被控对象,从泄流阀改变湿侧的含湿量和压力到作用到膜加湿器干侧的过程中,存在内部参数影响、负载变化、环境改变等多种不确定性干扰。而自抗扰控制结构中的扩张状态观测器ESO 具有放大和监测总干扰的能力,同时,fal滤波函数具有对干扰信号、噪声信号滤波的能力,适合解决这种复杂不确定系统的控制问题。

假设中冷水流量调至最大,电堆入口的温度值始终稳定在设定值附近,而正常工况下的电堆入口相对湿度在60%至80%之间,此时可以将空气相对湿度等同于空气含湿量,且相较于露点温度,相对湿度更适合于用来分析系统特性。所以反馈信号可选定电堆入口处的相对湿度。

根据图2所示的膜加湿器结构和质量守恒定理,膜加湿器干湿侧有

式(10) 中,̇mv,dry,̇mv,wet,̇mv,dry,in,̇mv,dry,out,̇mv,wet,in和̇mv,wet,out为干侧内、湿侧内、干侧入口、干侧出口、湿侧入口和湿侧出口的水蒸气流量。

若将膜加湿器干侧出口(即电堆入口)处的湿度Hca,in等同于膜加湿器干侧内的湿度Hdry,根据理想气体状态方程,有

式(11)中,Vdry为干侧体积;Rv为水蒸气的气体常数;psat（Tdry） 为干侧温度Tdry下的饱和蒸汽压,可由式(12)计算[11]:

式(12)中,T为温度,单位℃。

进入膜加湿器的湿气来自于电堆,电堆出口水蒸气流量为̇mv,ca,out,压力为pv,ca,out,相应的总气体压力为pca,out,根据理想气体状态方程,有

式(13)中,̇mrv为流出泄流阀的气体流量,由阀门内外压差Δp和开度φrv决定。选用与节气门同种型号的阀门作为泄流阀。

整理式(10)-(14)可得式(15)-(18):

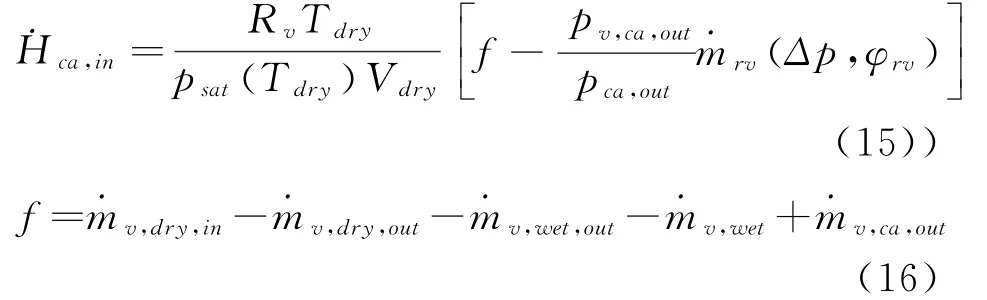
根据自抗扰控制原理,系统总干扰为:

各项输入量和输出量以及状态量分别为

3.3 模型仿真验证

可根据上述自抗扰控制原理与对系统的分析搭建空气湿度控制器Simulink模型,如图9所示。将所建立的空气湿度控制器模型加入系统模型和流量压力控制器模型中进行仿真,此时中冷水流量调至最大。根据计算和调试后的控制器参数的选取如表4所示。

表4 湿度控制器控制参数

图9 空气湿度控制器Simulink模型

由于膜加湿器处于空气系统中段,并不能直接通过环境状态判断此时膜加湿器的加湿情况。所以通过改变环境条件来验证湿度控制策略并无必要。本文在一定阶跃工况场景下,设定空气湿度目标为40%,观察入堆空气状态情况如图10所示。

可以看出,在工况不断切换的过程中,空气流量和压力始终跟随电堆需求稳定变化,说明此时流量压力控制器控制效果良好。在流量和压力突变的过程中,空压机出口空气温度也会出现突变,此时会造成图10中的入堆空气温度出现短暂突变。这一突变为相对湿度值突变的主要原因,但只要能保证温度能快速稳定在设定值,相对湿度最终也能稳定在设定值。

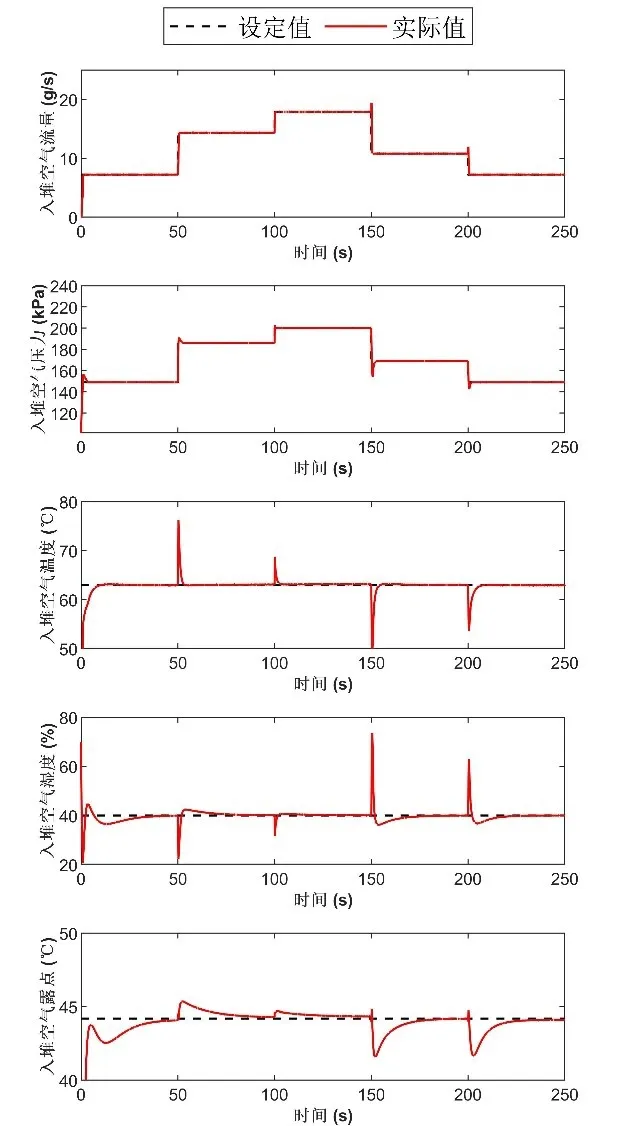
图10 控制器控制情况

从图10中可以看出,相对湿度的超调量少于3%,响应速度在20s以内。此外,从空气露点情况来看,空气露点始终能稳定在设定值附近,证明该湿度控制器在流量、压力、温度均稳定调控的前提下可以稳定控制空气含湿量。

4 结 语

提出了一种外增湿空气系统湿度可控方案。首先设计了变量实验对关键膜加湿器模型进行了验证,保证湿度模型精度符合使用需求。然后结合空气系统模型和流量压力控制器模型,在流量、压力和温度均被稳定调控的情况下,分析对比了三种主动调控湿度的空气系统拓扑结构改进方案,最后选定比例阀位置为膜加湿器湿侧入口的泄流阀作为主动调节空气湿度的手段。最后采用了自抗扰控制设计空气湿度控制器来对泄流阀进行控制,模型仿真结果显示相对湿度控制效果理想,其超调量少于3%,响应速度在20s以内。