耦合天气雷达定量降水估计与定量降水预报的中小流域洪水预报研究
2022-06-27糜佳伟田济扬楚志刚刘荣华薛海
糜佳伟, 田济扬, 楚志刚 , 刘荣华 , 薛海
(1.华北水利水电大学,河南 郑州 450046; 2.中国水利水电科学研究院,北京 100044;3.水利部防洪抗旱减灾工程技术研究中心,北京 100044; 4.南京信息工程大学,江苏 南京 210044;5.南京山禹云雷物联网科技有限公司,江苏 南京 210044)
在降雨监测方面,天气雷达具有高时空分辨率的特点,较地面雨量站能更准确测得降雨的时空分布特征[1],适用于汇流时间短且需要实现精准预报的中小流域。基于天气雷达探测资料的降雨临近预报的结果较数值降雨预报的精度高,该预报方式是延长中小流域洪水预报预见期的重要技术手段。笔者耦合天气雷达定量降水估计(Quantitative Precipitation Estimate,QPE)和定量降水预报(Quantitative Precipitation Forecast,QPF)开展中小流域洪水预报研究。
天气雷达QPE的精度主要受Z-R关系影响,不同类型降雨的Z-R关系不同[2],Z指雷达反射率,R指降雨强度。实际中常用的Z-R关系式为Z=200R1.6和Z=300R1.4[3-4],但此关系式不适用于不同天气雷达和不同类型降雨场次的情况,导致天气雷达QPE不易被直接应用于中小流域洪水预报中。为了延长洪水的预见期,开展天气雷达临近降雨预报非常必要。降雨预报的主要方法包括交叉相关系数法[5]、单体质心法[6]和光流法[7]等外推法。
目前,已有少量关于耦合天气雷达QPE与QPF的流域洪水预报的研究,但预报精度有待提高。殷志远等[8]将4种天气雷达降雨预报结果输入到半分布式模型TOPMODEL中对湖北漳河流域进行径流模拟,验证结果表明,动态Z-R关系较通用Z-R关系下的雷达降雨反演的精度高,径流模拟效果好;许继军等[9]在将天气雷达监测雨量作为GBHM(Geomorphology-Based Hydrological Model)分布式水文模型的输入量进行三峡区间洪水过程模拟时指出,雷达预测能捕获降雨的空间分布,经地面雨量站数据校正后,与GBHM分布式水文模型的结果相结合,可提高洪水预报的精度;严昌盛等[10]分别将天气雷达和地面雨量站的雨量监测数据、雷达临近降雨预报数据输入模型PDM(Probability Distributed Model)中,对王家坝以上流域(约30 672 km2)洪水进行模拟,结果表明,雷达临近降雨预报的精度基本满足实时洪水作业预报的要求,同时该精度有很大的提升空间。
福建省位于我国东南沿海地区,山丘区众多,加之受季节性台风影响,强降雨引发的洪涝灾害多发,严重威胁人民的生命财产安全[11-12]。笔者以福建梅溪流域为研究区,选取2012年的“苏拉”、2014年的“海贝思”、2016年的“尼伯特”3场台风引发的降雨洪水过程为研究对象,采用强降水识别、光流法等技术手段获取较为准确的天气雷达QPE和QPF结果,并将其作为梅溪流域分布式水文模型的输入,开展洪水预报研究,分析耦合天气雷达QPE与QPF的中小流域洪水预报的效果,探究该方法在中小流域洪水预报中的适用性。
1 研究区与数据
1.1 流域概况
梅溪是闽江的一级支流,发源于闽清县南部,流域面积956 km2,在东南沿海地区具有很强的代表性[13]。流域多年平均降雨量1 560 mm。受台风和地形影响,年内降雨主要集中在4—9月,局地短历时强降水时有发生,致使流域内洪涝灾害频发。自1949年以来,流域内发生洪灾20余次。历史最大洪水发生于2016年7月9日,强降雨引发的洪水洪峰流量达到4 710 m3/s。
1.2 数据资料
天气雷达选用福州市长乐区境内的S波段雷达(以下简称长乐雷达),数据来源于国家气象局,并通过数据质量控制。长乐雷达扫描区域半径为250 km,梅溪流域几乎全部落在雷达扫描半径为100 km的范围内,这样可保证雷达扫描数据的质量,具体如图1所示。

图1 雷达覆盖范围与流域位置
流域内共有8个雨量站、1个水文站,如图2所示。长系列降雨径流资料用于流域分布式水文模型的参数率定与验证,该资料由福建省水利水电科学研究院提供。从所测到的数据中选取2012年的“苏拉”、2014年的“海贝思”、2016年的“尼伯特”3场台风在梅溪流域引发的典型降雨洪水事件(见表1和如图3所示)为研究对象,开展耦合天气雷达QPE与QPF的中小流域洪水预报研究。

图2 雨量站、水文站与流域位置的关系

表1 3场降雨洪水事件的具体情况

图3 实测降雨洪水过程
流域下垫面资料主要用于分布式水文模型的构建,包括1∶5×104DEM、土地利用和植被类型、土壤类型等数据[14]。
2 模型与方法
2.1 雷达降水反演及临近预报模型
通过建立Z-R关系可实现雷达降水反演,但受降水类型等因素的影响,Z-R关系差异较大。正确的降水分类有助于建立不同类型下不同的Z-R关系,通过强降水识别技术[15]对不同时段、不同空间位置的场次降雨进行分类,识别出强降水区域,分别建立强降水区与非强降水区的Z-R关系,从而提高天气雷达的预报精度。经过30场历史降雨资料的反复试验,最终确定了强降水区的Z-R关系为Z=135R1.33,其它降水区的Z-R关系为Z=200R1.6。
依托STEPS(Short Term Ensemble Prediction System),在上述降水反演结果的基础上,利用光流法[16-18]开展雷达临近预报研究。为降低预报的不确定性,通过高斯扰动构建了30个集合预报成员,形成临近集合预报集,获得3场降雨1、2、3 h预见期的预报结果。
2.2 基于中国山洪水文模型的梅溪流域分布式水文模型
中国山洪水文模型(China Flash Flood hydrological model,CNFF)是由中国水利水电科学研究院自主研发的分布式水文模型,模型的基本原理见文献[19],模型结构如图4所示。该模型的主要特色与优势为:①基于高精度的地形地貌数据和考虑雨强影响的分布式单位线技术;②资料缺乏地区河道洪水演进变参数计算方法;③连续和不同场次过程暴雨洪水实时模拟和预估预报。依托CNFF框架,结合梅溪流域特征及资料,构建梅溪流域分布式水文模型,模型参数采用参考文献[20]的研究成果。该模型的概化图如图5所示。
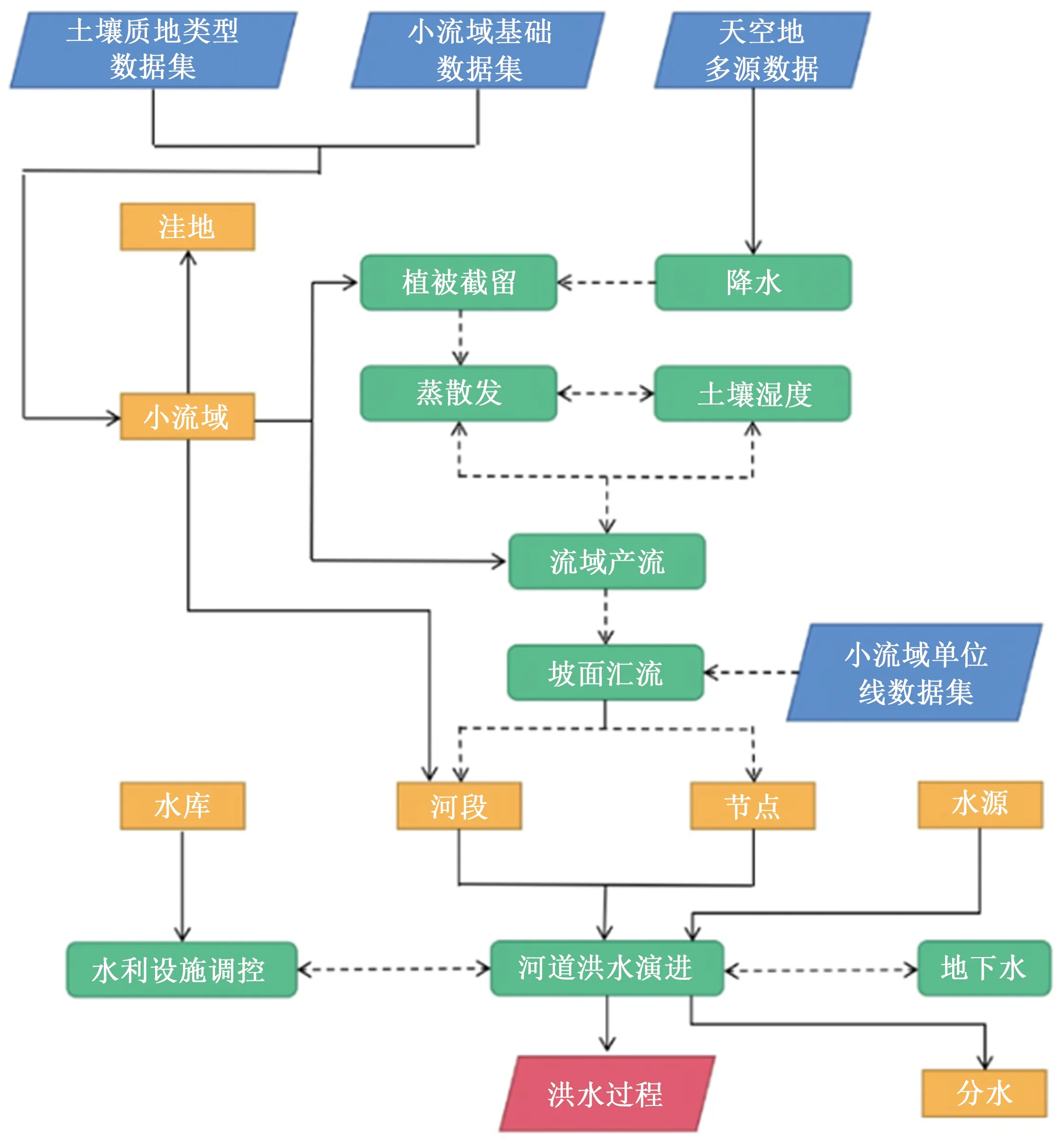
图4 CNFF水文模型结构示意图

图5 梅溪流域分布式水文模型概化图
2.3 评估方法
2.3.1 雷达测雨结果与临近预报结果评估方法
雷达测雨结果与临近预报结果评估方法中选用24 h累积雨量的相对误差(RE)和均方根误差RMSE两个指标。
1)累积雨量相对误差(RE)的计算式为:

(1)
式中:P′为雷达反演的面累积降雨量,mm;P为地面站观测的面累积降雨量,mm。P′为流域内雷达所有网格点雨量的均值,P则根据梅溪流域内雨量站的降雨数据采用泰森多边形法求得。
2)均方根误差(RMSE)的计算式为:
(2)
式中P′j和Pj分别为雷达降水反演值与地面雨量站观测的降雨量值。当进行空间尺度评价时,M为雨量站个数,P′j和Pj分别为在某一特定的空间位置j处整个观测时段内累积雨量的雷达反演值与地面雨量站的观测值;当进行时间尺度评价时,M为降雨时长,P′j和Pj分别为在观测时刻j时研究区面平均雨量的雷达反演值与地面雨量站的观测值。为了去除不同场次降雨量的影响,最终求得的RMSE值为分别除以相应维度地面雨量站观测值的平均值。
2.3.2 洪水预报评估方法
采用洪峰流量相对误差(REQ)、洪峰时间误差(TP)、确定性系数(NSE)等对梅溪流域分布式水文模型的洪水预报结果进行评价。各评价指标分别由下面的公式计算:
(3)
TP=TSP-TOP。
(4)
(5)
3 结果与分析
3.1 强降水识别效果
为说明强降水识别的效果,选用福建长乐雷达常用的Z-R关系(Z=200R1.6)对降水进行了反演,结果见表2。由表2可知,对于3场典型降雨,基于强降水识别的雷达QPE 24 h累积雨量相对误差较常规反演的分别提高了60.84%、49.03%和68.52%,降雨时空分布得到了明显改善。

表2 通过常规反演与强降水识别反演的降雨评估结果
3.2 基于强降水识别的临近预报结果
雷达临近降水预报集合共30个成员,采用30个成员预报结果的平均值作为最终的临近预报结果。3场典型降雨不同预见期的临近预报结果见表3。
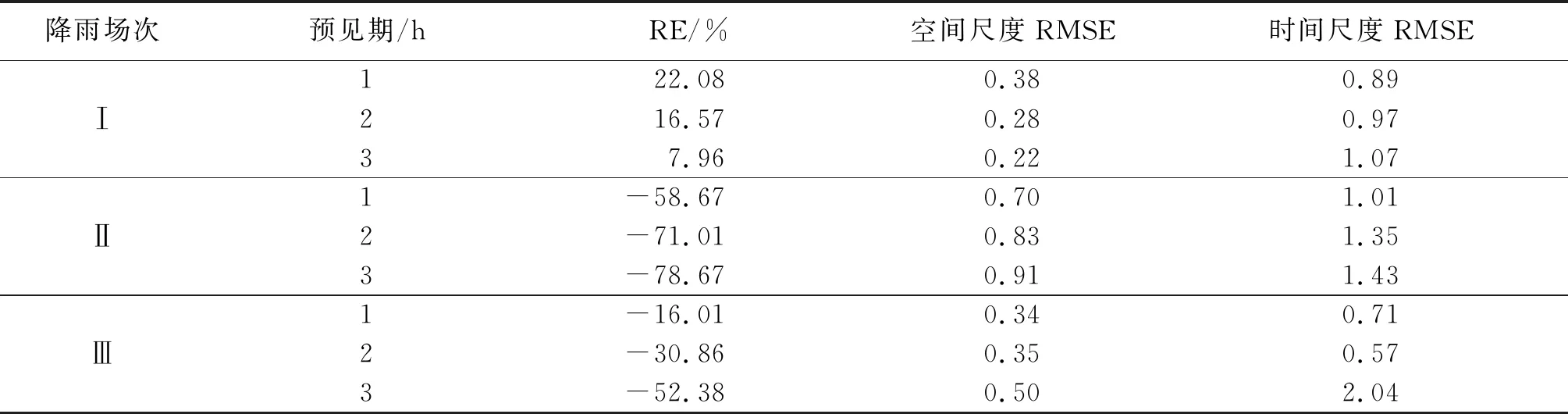
表3 基于强降水识别的降雨临近预报评估结果
由表3可知,降雨场次Ⅰ的预报效果最佳,临近降水预报结果相对可靠,降雨场次Ⅱ和Ⅲ的预报效果不理想。
3.3 基于雷达QPE的洪水预报
将经过强降水识别的雷达反演降雨量,作为梅溪流域分布式水文模型的输入进行洪水预报,结果见表4和如图6所示。
由表4和图6知:降雨场次Ⅰ的洪峰流量相对误差为-35.7%,洪峰时间误差为-0.3 h,确定性系数为0.68;场次Ⅱ的洪峰流量相对误差为-13.7%,洪峰时间误差为-1.0 h,确定性系数为0.90;场次Ⅲ的洪峰流量相对误差为6.9%,洪峰时间误差为-3.2 h,确定性系数为0.57。

表4 耦合雷达QPE的洪水预报效果

图6 基于雷达QPE的洪水预报结果
3.4 基于雷达QPF的洪水预报
将不同预见期的雷达临近预报降雨量,作为梅溪流域分布式水文模型的输入量进行洪水预报,结果见表5和如图7所示。
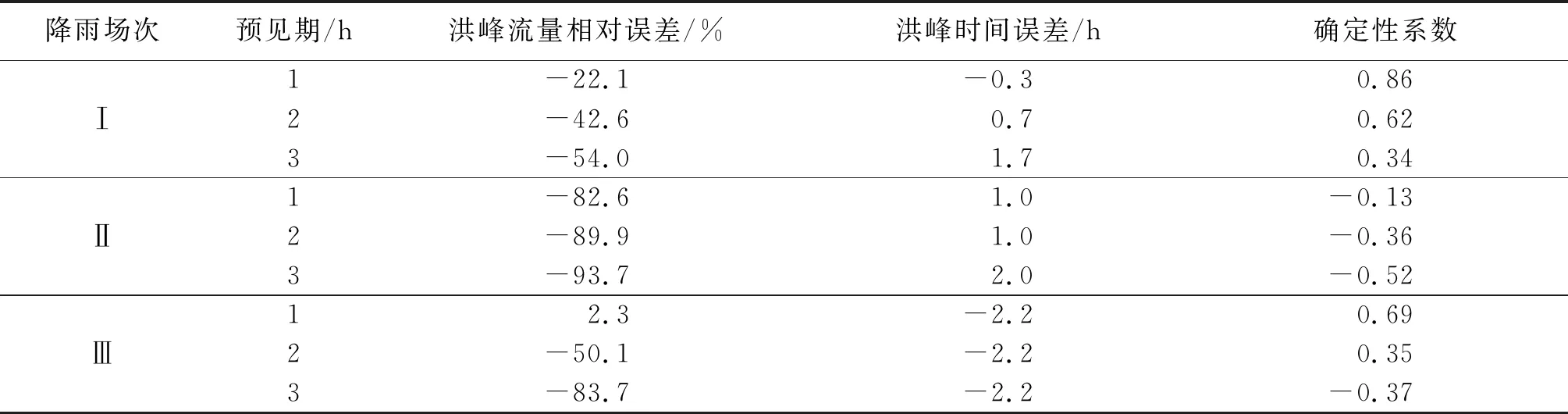
表5 基于雷达QPF的洪水预报效果
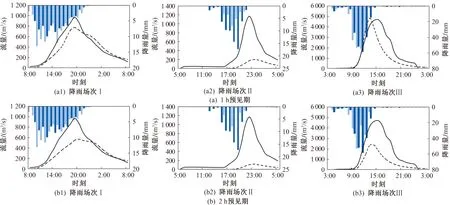

图7 基于雷达QPF的洪水预报结果
由表5和图7知:对于降雨场次Ⅰ,耦合1、2、3 h预见期雷达QPF计算的洪峰流量相对误差分别为-22.1%、-42.6%、-54.0%,洪峰时间误差分别为-0.3、0.7、1.7 h,确定性系数分别为0.86、0.62、0.34;对于降雨场次Ⅱ,耦合1、2、3 h预见期雷达QPF计算的洪峰流量相对误差分别为-82.6%、-89.9%、-93.7%,洪峰时间误差分别为1.0、1.0、2.0 h,确定性系数分别为-0.13、-0.36、-0.52;对于降雨场次Ⅲ,耦合1、2、3 h预见期雷达QPF计算的洪峰流量相对误差分别为2.3%、-50.1%、-83.7%,洪峰时间误差分别为-2.2、-2.2、-2.2 h,确定性系数分别为0.69、0.35、-0.37。
总体上,场次Ⅰ的洪水预报结果较好,而场次Ⅱ和Ⅲ的预报结果无法满足实际需要。随着降雨预见期的延长,洪水预报精度明显降低。
3.5 洪水预报的误差分析
为进一步分析耦合雷达QPE和QPF的洪水预报误差来源,分别用实测降雨量驱动梅溪流域分布式水文模型,计算洪水评估指标值,将各评估指标的结果作为分布式水文模型自身的误差(见表6);耦合雷达QPE和QPF计算的各评估指标误差为耦合系统的总误差,采用总误差的绝对值减去分布式水文模型的误差绝对值的结果,认为是降雨量偏差导致洪水预报误差。洪峰流量误差、洪峰时间误差和确定性系数误差分别记为ΔRER、ΔREQ、TP、ΔNSE,各项指标计算结果见表7和表8。

表6 分布式水文模型的洪水预报误差

表7 雷达QPE偏差的洪水预报误差
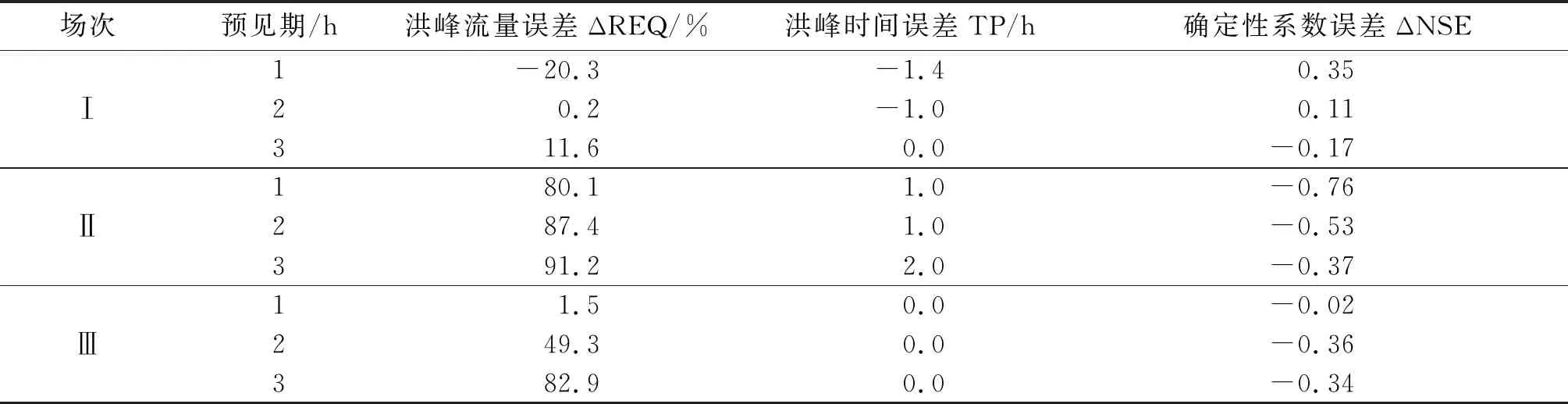
表8 雷达QPF偏差导致的洪水预报误差评估
由表4、6和7可知:对于降雨场次Ⅰ,基于雷达QPE开展洪水预报的误差较基于雨量站测雨数据开展洪水预报的误差小,说明尽管总雨量存在一定偏差,但由于空间尺度和时间尺度的RMSE值较小,雷达QPE的结果适宜作为分布式水文模型的输入,在描述降雨时空分布特征方面具有一定优势;对于降雨场次Ⅱ、Ⅲ,基于雷达QPE开展洪水预报的误差较基于雨量站测雨数据开展洪水预报的误差大,说明当总雨量、降雨时空分布均存在较大偏差时,雷达QPE的预测结果的偏差会导致洪水预报结果的精度变差。
由表5、6和8可知:对于降雨场次Ⅰ,基于1 h预见期的雷达QPF开展洪水预报的误差较基于雨量站测雨数据开展洪水预报的误差小,说明当总雨量偏差不大时,由于雷达的预测结果能准确反映降雨量的时空分布,有助于改善分布式水文模型洪水预报结果,但随着雷达QPF预见期的延长,总雨量和降雨量的时空分布的偏差变大,导致洪水预报结果的精度变低;对于降雨场次Ⅱ、Ⅲ,由于雷达QPF测得的总雨量偏差太大,耦合雷达QPF的洪水预报结果误差大幅增加。
4 结论
以梅溪流域为研究区,选取2012年的“苏拉”、2014年的“海贝思”、2016年的“尼伯特”3场台风引发的降雨洪水过程为研究对象,采用强降水识别、光流法等技术手段获取更为准确的天气雷达QPE和QPF的降雨数据作为梅溪流域分布式水文模型的输入开展洪水预报研究,分析耦合天气雷达QPE与QPF的中小流域洪水预报效果,主要结论如下:
1)强降水识别能有效提升天气雷达QPE的降雨监测精度,对于强降雨预报精度的改进效果明显;随着降雨预见期的延长,天气雷达QPF的预报精度显著降低;对于降雨量时空分布较为均匀的降雨,天气雷达QPE和QPF的预报结果将更加准确。
2)对于降雨量时空分布较为均匀的降雨,耦合天气雷达QPE的洪水预报较雨量站测雨更具优势,耦合1 h预见期天气雷达QPF预报结果能够满足中小流域洪水预报的要求。
3)对于短历时强降雨和特大暴雨,受天气雷达QPE和QPF预报精度的影响,洪水预报效果较差,较难满足中小流域洪水预报的要求。
进一步研究中将充分考虑云层结构及水汽的物理变化与演化,结合天气雷达对气象要素空间探测的能力,在光流法等传统雷达外推算法的基础上,引入气象动力学的物理概念,重点探究短历时强降雨和暴雨的临近预报方法,提高耦合天气雷达QPF的洪水预报精度。
