粒子群优化算法对配电网无功的优化分析
2022-06-26刘新鑫牛元锋
刘新鑫,牛元锋
(1.山东天祥电力设计院有限公司,山东 济南 250101;2.郑州科锐同源电力设计有限公司 济南分公司,山东 济南 250100)
0 引 言
配电网无功优化是一个多变量、多约束的非线性优化问题,国内外学者对该问题进行了大量研究,认为有功网损的优化目标无法有效实现无功优化,需要设置相关权重和阈值[1]。目前,遗传算法、蚁群算法以及禁忌搜索算法等智能算法的出现弥补已有算法的不足,并在配电网领域广泛应用。在此情况下,本文提出了一种粒子群算法,从经济性和稳定性等方面分析网损、电压偏差、无功补偿等多目标的优化问题[2]。
1 配电网无功优化的数学模型
配电网线路模型如图1所示。
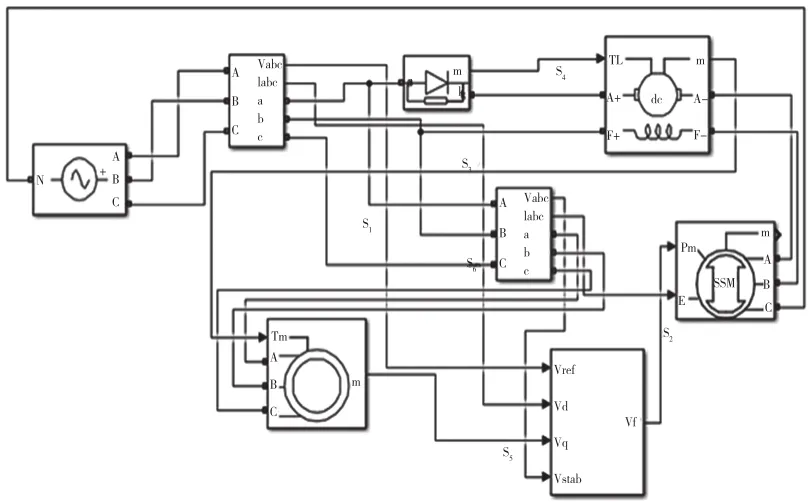
图1 配电网的数学模型
图1是由S个输电线组成的配电网系统,各线路的电流可以表示为:

式中,Qi是配电网的潮流;Ui为i线路的电压;Ri为i线路的电阻。任何一条线路S处于无功状态都会改变配电网整体的电流分布,所以图1中任意线路S的电流I′可以表示为:

式中:I1为线路1的电流;s为无功线路的集合;Si采用特殊解的形式判断其是否为无功线路,主要判断各线路中的I是否出现变化ΔI,1代表存在电流差异,0代表电流无差异[3]。ΔI的具体计算公式为:

引入电流系数τ,以调节线路中原有电阻R对电流I的影响。依据式(3)将式(1)与式(2)合并,可以得到式(4),具体为:

式中,ns为线路的初始集合,主要是依据线路的电阻R进行判断,一般为0.23。
2 配电网无功判断模型
配电网无功判断是依据各线路的潮流S、电流变化进行判断[4]。其中,线损、电压偏差的计算公式为:

式中,Gk为电导;cosθi为相邻两线的夹角。
线路S的电压约束为:

输电线路的传输功率约束为:

式中,Pi为线路i的功率。
线路电阻约束为:

线路无功补偿容量约束为:

3 基于粒子群优化算法的配电网算法构建
依据式(1)~式(9)可知,ΔI与配电网无功有相关性。实际上,配电网中任意线路S出现无功现象[5]。一般来说,调节τ可以进行有功、无功两种情况判断[6]。
3.1 确定调节系数τ
在无功情况下,对ΔI进行一阶导数,求得其最大值,其计算公式为:
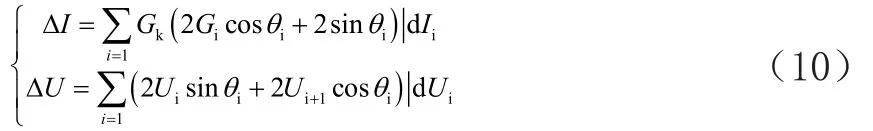
在无功情况下,对ΔU进行二阶偏导数,求得ΔU的最大值[7],计算公式为:

为了提高判断结果的精准度,缩短判断时间,要对无功进行优化[8],得到:
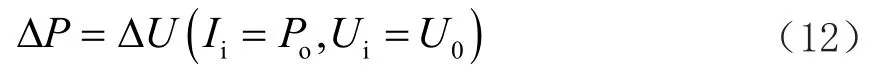
依据上述条件,求得无功线路所在的可能位置,其计算公式为:

式中,C为方案;M为母线到无功线路的可能路径。
3.2 粒子群优化算法的计算步骤
粒子群优化算法需要明确配电网S线路所在的位置,具体计算步骤如下[9]。一是录入各线路S的基础数据;二是依据线路S数据,构建无功判断矩阵;三是计算配电网各线路的潮流、电压以及电流[10];四是依据相应的潮流得到最小的电流、最大的电压[11]。
4 IEEE 33算例解析
本文以IEEE 33作为研究对象,对粒子群优化算法进行验证,计算其无功优化判断效果。
4.1 计算时间
为了比较粒子群算法的效果,对比最大潮流、最高电压、最小电流等算法,计算单目标的无功判断结果,如表1所示。

表1 单目标的无功判断分析
对双目标线路进行测试,结果如表2所示。
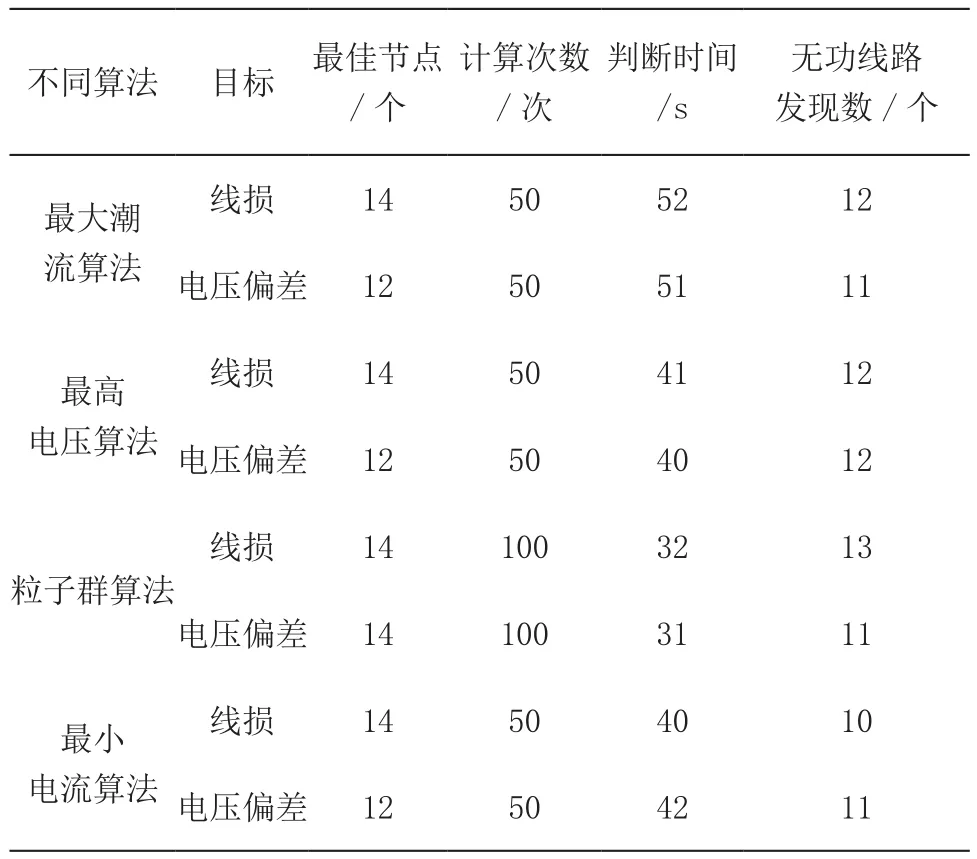
表2 双目标的无功判断分析
为了更加准确地进行粒子群算法的验证,要对其进行多目标无功判断分析,结果如表3所示。
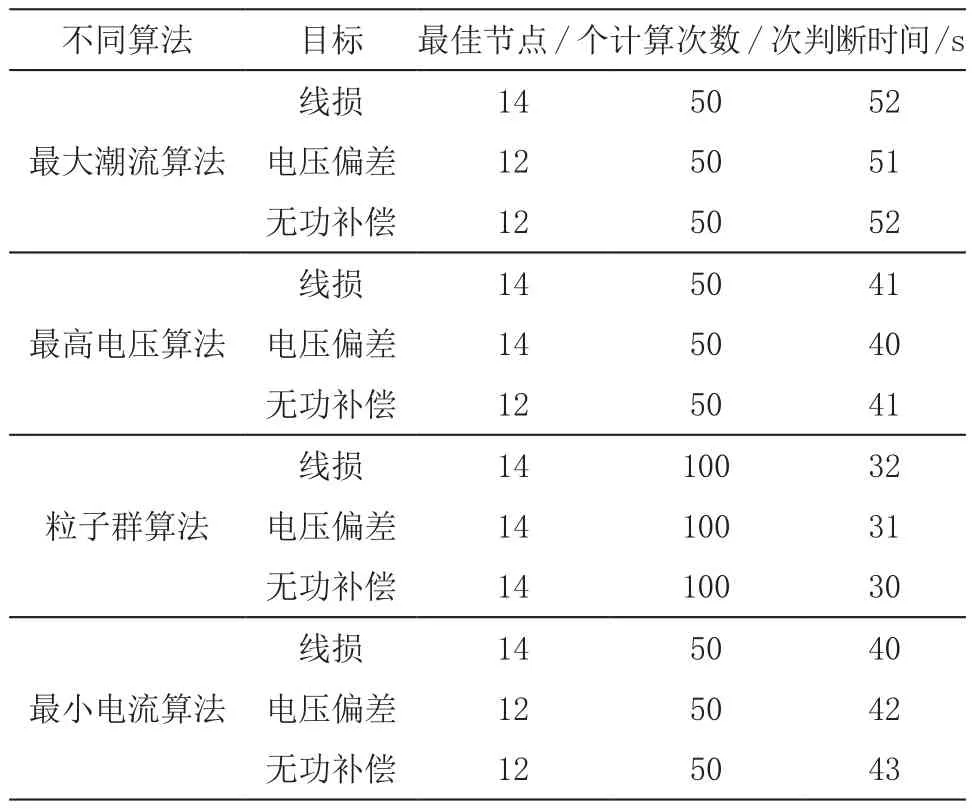
表3 多目标的无功判断分析
相对其他3种算法来说,粒子群优化算法线损、电压偏差、无功补偿的计算时间均最少,计算次数为100次,最佳节点为14个,均优于其他算法。
4.2 不同原因下的无功优化结果
为了验证粒子群算法在线损、电压偏差、无功补偿方面的判断结果,针对以下4种情况进行判断,比较判断结果的准确性。其中,目标A包括线损无功、无功补偿;目标B包括线损无功、电压偏差无功;目标C包括无功补偿无功、电压偏差无功;目标D包括线损无功、电压偏差无功、无功补偿,不同目标下的无功判断结果如表4所示。
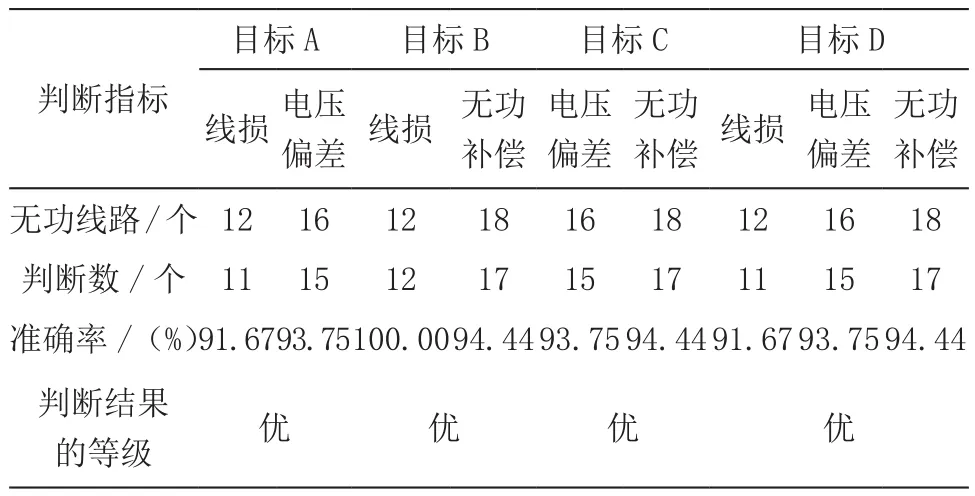
表4 不同类型的无功优化结果
依据表4的结果可知,在多目标下粒子群算法的无功判断结果更加准确,而且可以实现多目标(线路、电压偏差、无功补偿等原因所致的无功)的准确判断,说明粒子群算法可以实现配电网无功优化。
5 结 论
本文针对配电网无功优化的问题提出一种粒子群优化算法,将粒子群与无功判断相结合,用IEEE 33进行案例分析。结果显示,粒子群优化算法在计算时间、单次计算节点数、判断准确性方面优于最高电压、最小电流、最大潮流等算法,可以实现配电无功的优化。
