多元线性回归模型的异方差问题的浅析

尚云艳 祝师强 孙浩

摘 要：“应用回归分析”课程是高校应用统计学专业均开设的专业核心课程，多元线性回归模型是非常重要的知识内容，但是由于其理论内容复杂，学生学习难度大，针对此问题，本文从权的概念出发，利用权倒数的性质论证了加权线性回归的合理性。并以北京市15个经济开发区的销售收入数据为例，运用加权最小二乘估计方法改进模型，最后从残差图和拟合值绝对误差（率）两个方面进行比较，结果均表明加权线性回归效果好。该方法应用于教学，为教学内容的设计提供了新的思路，便于学生掌握并深入学习。

关键词：异方差;加权最小二乘估计;残差分析;权

文献标识码：A

回归分析的发展经历了很长的一段历史，早在18世纪，F.Galton提出利用最小二乘原理进行回归分析[1]，从那时开始，回归分析就越来越备受关注，但是随着回归分析的普及，在实际应用中往往出现违背线性回归假设的情况，比如，随机误差异方差、随机误差存在序列相关性、数据观测值异常等问题[2]。特别是对随机误差异方差的情况，加权线性回归是对普通线性回归的一种改进，但是文献[3-4]中并未证明加权线性回归的合理性。回归诊断是回归分析中必不可少的内容，由于回归假设都是针对随机误差项提出的，所以要从分析随机误差项ε的估计量（残差）入手，通过从残差和残差图分析来考察模型的合理性[5]。

本文主要讨论在随机误差异方差的情况下，怎样建立合理、合适的模型。根据以往的经验，处理随机误差异方差问题的方法有加权最小二乘法（WLS）、BOX-COX变换法和方差稳定性变换法，这些方法应用于实际，可以消除或者减弱异方差对拟合模型造成的不良影响。教科书上仅对加权线性回归的原理有所介绍，但是并没有涉及其本质内容。本文通过权、权函数、权倒数的性质揭示了加权线性回归的本质，论证了其合理性。以北京市经济开发区的销售收入数据为例，利用加权最小二乘法建立数学模型，并且进行比较分析，模拟结果表明加权线性回归比普通线性回归有一定的改进之处。

1 线性回归的基本假定[6-7]

线性回归模型I（矩阵形式）

4 实例分析

4.1 问题描述

本文数据来源于文献[6]，因变量Y为各开发区的销售收入（百万元），自变量X1为截至1998年底各开发区累计招商数目，X2为招商企业注册资本（百万元），15个开发区的具体数据如表1所示。

从因变量Y的直方图（图1）也可以看出销售收入信息呈右偏态分布，即数据具有异方差特征。

4.2 多元线性回归模型

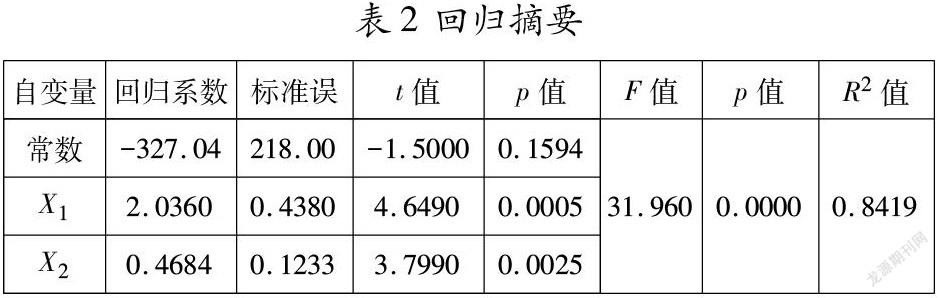
若对上述数据进行最小二乘回归，得到结果如表2所示，造成回归系数方差较大且不能通过显著性检验的原因可能是异方差性;另外，模型的决定系数为0.8419，拟合度值并不高，有提高的可能性。

4.3 加权线性回归模型的建立

由于4.2中普通残差的绝对值与自变量X中X1的等级相关系数为0.4429，与X2的等级相关系数为0.7214，于是根据2.1，选择X2构造权函数，即W=diag（1Xm1，1Xm2）。

根据对数似然值越大，回归模型拟合效果越好的原则，表3列出了m值的选择过程。

表3表明，当m=2.5时，对数似然统计量的值最大，于是m的最优值为2.5。同时，回归模型结果如表4所示。

与表2相比，表4中常系数方差变小，且通过了显著性检验，另外，模型决定系数为0.8494也大于之前的0.8419。

4.4 方法比较

对加权线性回归模型做残差图，结果如下所示：

图2中，从左至右图形中的大部分散点并没有向外侧扩散，反而有收敛趋势，可见“权”对异方差问题有一定的修正效果。

普通最小二乘和加权最小二乘的拟合值与残差的比较结果如表5所示，显然，加权最小二乘的效果较好。

4.5 回归诊断

从图示结果可以看出，图3中残差值并未出现极端上升或下降趋势，是随机均匀分布的。

結语

本文对多元加权线性回归模型的原理与本质内容作了梳理，利用权倒数的性质，论证了加权线性回归的参数估计也具有“最优”无偏性，同时结合数据案例验证了加权线性回归是解决异方差问题的有效途径，不管是从残差图还是拟合值绝对误差来讲，效果都有所改善，回归诊断结果也表现良好，即模型较优。文章的理论为以后的教学和学生学习运用加权线性回归解决此类问题提供了充分的理论依据，为学生深入学习多元线性回归模型提供了更多的可能性。

参考文献：

[1]G.A.F.塞伯.线性回归分析[M].方开泰，等，译.北京：科学出版社，1987，1.

[2]Fabsitz，R.et al.Regression Analysis of Data with Correlated Errors.An Example from the NHLBI Twin Study[J].Chron.Dis.1985，38（2）：165.

[3]何晓群，刘文卿.浅谈加权最小二乘法及其残差图[J].统计研究，2006（4）：53-57.

[4]林天水，陈佩树.一元线性回归中异方差的处理[J].统计与决策，2015（17）：86-88.

[5]胡菊华.基于残差分析的线性回归模型的诊断与修正[J].统计与决策，2019（24）：5-8.

[6]何晓群，刘文卿.应用回归分析[M].北京：中国人民大学出版社，2012.

[7]茆诗松，程依明，濮晓龙.概率论与数理统计[M].北京：高等教育出版社，2012.

基金项目：2021年度陕西省教育科学“十四五”规划一般课题“理实一体化的BOPPPS与‘六个下功夫相融合下数学教学模式创新研究”（编号：SGH21Y0293）;2020年11月陕西省教育部产学合作协同育人项目“大数据下的数学课程教学模式改革与实践”（编号：202002021019）

作者简介：尚云艳（1986— ），女，陕西咸阳人，硕士，讲师，研究方向：质量控制。FEA13F87-8594-4C1A-B251-F71883B69B98