Volume Inequalities for Sections and Projections of Asymmetric Convex Bodies

--

(1. School of Mathematics and Information Science, Henan Polytechnic University, Jiaozuo 454000,China; 2. School of Science, Zhejiang University of Science and Technology, Hangzhou 310023, China)

Abstract: In this paper, we establish volume inequalities for k-dimensional sections and projections of convex bodies (not necessarily symmetric) and their polars in a more general position than John’s position.

Keywords: Section; Projection; Asymmetric; Brascamp-Lieb inequality

§1. Introduction

The main result of this paper is stated as follows.

Note that when all (ai)m1are equal to 1, Theorem 1.1 reduces to the results established by Alonso-Guti´errez and Brazitikos [1]. Our proofs are based on the ideas developed by Ball [3,4],Barthe [5], Alonso-Guti´errez and Brazitikos [1], that the geometric Brascamp-Lieb inequality and its reverse (see Lemma 2.1) play an important role.

The rest of this paper is organized as follows. In Section 2 the background materials are collected. Section 3 contains several auxiliary lemmas. Our main results will be proved in Section 4.

§2. Background materials

We collect some basic definitions and notations in convex geometry. General references are the books of Gardner [9] and Schneider [20].

Throughout the paper, Rnstands forn-dimensional Euclidean space (n≥2) equipped with a Euclidean structure〈·,·〉. We write‖·‖for the Euclidean norm on Rn. A convex bodyKin Rnis a compact convex set with nonempty interior whose support functionh(K,·):Rn →R is defined by, forx∈Rn,

Note that the Brascamp-Lieb inequality was first established by Brascamp and Lieb [6].The geometric form (2.4) due to Ball [3] played a critical role in solving reverse isoperimetric inequalities. By using the method of mass transportation, Barthe [5] found a new proof of the Brascamp-Lieb inequality and established the reverse Brascamp-Lieb inequality (2.5). He then used the inequalities to show new reverse isoperimetric inequalities, and also showed the uniqueness of equality cases of his and Ball’s reverse isoperimetric inequalities.

Obviously, taking trace in (2.3) immediately yields that

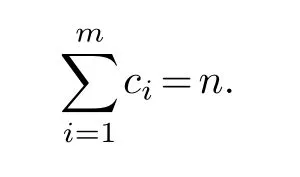
§3. Some lemmas

Form≥n, let (ui)m1be unit vectors in Rnand let (ci)m1be positive numbers satisfying condition(1.2). For ak-dimensional subspaceFof Rnwith 1≤k ≤n,the condition(1.2)induces a decomposition of the identity inF. Letζ={1≤i≤m:PF ui/=0}. For everyx∈Fandi∈ζ,we have

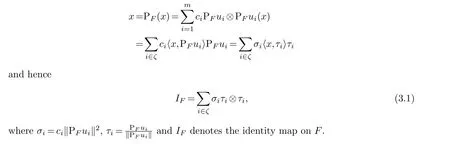
§4. Proof of the main result

Theorem 1.1 immediately follows from the following two theorems.

which gives the desired result.

Acknowledgment

The authors are indebted to the referee for the valuable suggestions and the very careful reading of the original manuscript.