层次分析法在城市道路设计中的应用

刘千石

（上海市园林设计研究总院有限公司，上海市 200031）

0 引 言

随着近年来我国社会经济水平的飞速增长，全国推进城市化的进程也在飞速前进中，随之而来的是私家车的保有量，以及城市道路货运交通的车辆数量大幅提升。城市路网作为城市的骨架，承担着市内外及过境交通，这对于城市道路的设计工作提出了更高的要求。道路设计作为城市路网建设中的重要环节，设计工作的合理性和科学性，都将是能否实现路网功能的关键因素。

现旨在通过在道路方案设计工作中，采用层次分析法，将方案的比较转换成量化比较，从而能够更加清晰地对比出某方案的优势和劣势。

1 层次分析法理论及数学模型

1.1 层次分析法理论

层次分析法的决策过程，包含了定性分析及定量分析。通过对决策目标的分析，分解出关于影响决策的不同影响因素，以及因素与因素之间、因素与不同方案之间的关系，从而构造出层次分析法的数学模型，来对不同方案进行排序比较，最终确定实现决策目标的最优方案[1]。

层次分析法的使用步骤如下：

（1）构造层次分析法数学模型；

（2）构造判别矩阵；

（3）层次单排序及其一致性检验；

（4）层次总排序及其一致性检验。

1.2 构造层次分析法数学模型

层次分析法是将决策的目标、影响因素和决策对象（待比选方案）分为三个不同层次，从高到低依次是：

（1）最高层级（目标层）；

（2）中间层级（指标层）；

（3）最下层级（方案层）。

结构模型如图1 所示：

图1 层次结构模型

1.3 构造判别矩阵

在构建完成层次结构模型后，需要对“指标层”中的各个影响因素进行两两比较，通过对比影响因素对决策目标实现的相对重要性，逐步确定各个影响因素的权重取值，并以此来构造判别矩阵，各因素的两两对比标度表如表1 所列。

表1 两两对比标度表

在确定各元素的赋值后，构成判别矩阵，如下式：

1.4 判别矩阵计算及其一致性检验

在计算出判别矩阵的特征值及特征向量后，为了验证权重取值是否合理，还需进行一致性检验。计算过程如下（设判别矩阵A 为n 阶正互反矩阵）：

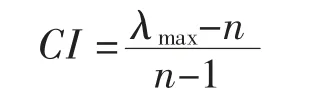
式中：λmax为判别矩阵A 的最大特征值；CI 为一致性指标。

定义RI 为平均随机一致性指标，其取值如表2 所列。

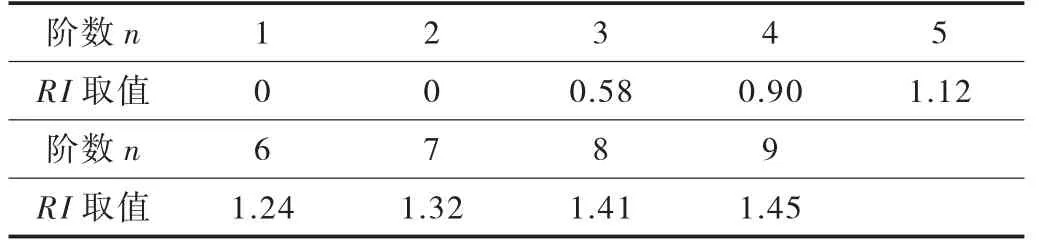
表2 平均随机一致性指标RI 取值表

设一致性比例：CR=CI/RI（n≥3；当n=1 或2 时，RI=0，因为1 阶矩阵及2 阶矩阵的判别结果总是一致的），计算结果按如下规则进行判别：

（1）当CR＜0.1 时，通过一致性检验；

（2）当CR≥0.1 时，未通过一致性检验，需适当调整判别矩阵及权重取值。

1.5 层次总排序及其一致性检验

为了从层次结构模型的总体上来检验累计的差异尺度，还需进行层次总排序的计算及一致性检验，计算过程如下：

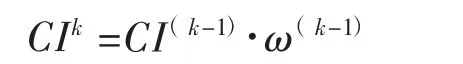
式中：CIk为第k 层各因素两两比较的层次单排序一致性指标；ω（k-1）为第k-1 层对总目标的总排序向量。

设：RIk=RI（k-1）·ω（k-1）

判别规则为：CRk＜0.1 当时，通过一致性检验。

2 应用案例1：道路横断面方案比选

在城市道路设计中，道路横断面的形式是否合理，将会直接影响道路未来的使用功能及景观效果。现运用层次分析法，构建层次结构模型，并根据不同的重要性，对不同的影响因素进行权重赋值，最终通过计算，得出每个方案的权重得分，选取权重得分最高的方案作为推荐方案。

2.1 项目背景

新汇路规划道路等级为城市次干路。新汇路南起奉贤区区界，北接上南路，全长约15 km，是贯穿浦江镇连接浦东新区与奉贤区的五条主要通道之一

该工程新汇路设计范围：南起跃进河桥接坡，北接现状先新路，设计长度约2.01 km，设计速度40 km/h，规划红线宽度40 m。其中一段新汇路建成后将连通先新路以北新汇路与新汇路大治河桥路段。该项设计拟对4 组横断面方案进行比选。

方案一：新汇路（申嘉湖高速—沈杜公路）路段

3 m 景观带+3.5 m 人行道+3.5 m 非机动车道+1.5 m 侧分带+7.5 m 机动车道+2 m 中央带+7.5 m机动车道+1.5 m 侧分带+3.5 m 非机动车道+3.5 m人行道+3 m 景观带=40 m 规划红线宽度。

方案二：新汇路（先新路—申嘉湖高速）路段

3.5 m 人行道+3.5 m 非机动车道+4.5 m 侧分带+7.5 m 机动车道+2 m 中央带+7.5 m 机动车道+4.5 m侧分带+3.5 m 非机动车道+3.5 m 人行道=40 m 规划红线宽度。

方案三：次干路典型断面

3 m 景观带+3.5 m 人行道+3.5 m 非机动车道+2.5 m 侧分带+15 m 机动车道+2.5 m 侧分带+3.5 m非机动车道+3.5 m 人行道+3 m 景观带=40 m 规划红线宽度。

方案四：两幅式型断面

1 m 绿带+3.5 m 人行道+3.5 m 非机动车道+11 m机动车道+2 m 中央带+11 m 机动车道+3.5 m 非机动车道+3.5 m 人行道+1 m 绿带=40 m 规划红线宽度。

2.2 横断面方案层次结构模型

道路横断面方案需要考虑多方面因素，来最终确定最科学合理的断面组成方案。此次新汇路横断面方案比选考虑的主要因素，按相对重要性排列如下：

（1）很重要

a. 交通需求因素；

b. 行车安全性因素；

c. 道路设计指标因素

d. 道路景观效果因素；

e. 经济性因素；

f. 用地因素。

（2）比较重要

a. 起终点路段衔接因素；

b. 未来改扩建便利性因素。

（3）一般重要：管线井盖影响因素。

根据以上因素建立横断面方案的层次结构模型，如图2 所示。

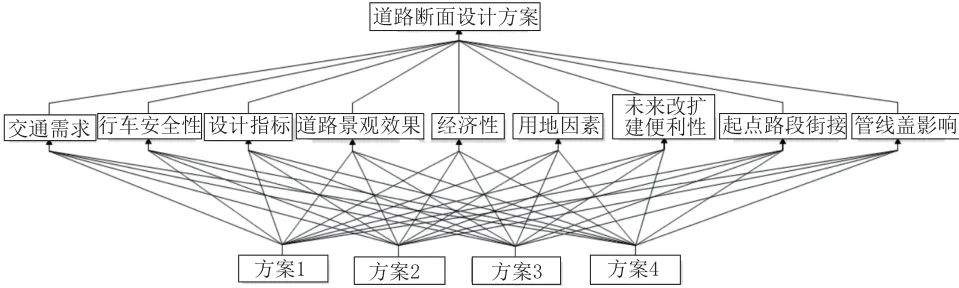
图2 道路横断面方案层次结构模型

2.3 层次单排序一致性检验

依据横断面方案层次结构模型构造的判别矩阵，分别计算最大特征值及特征向量及一致性比例，计算结果列于表3。

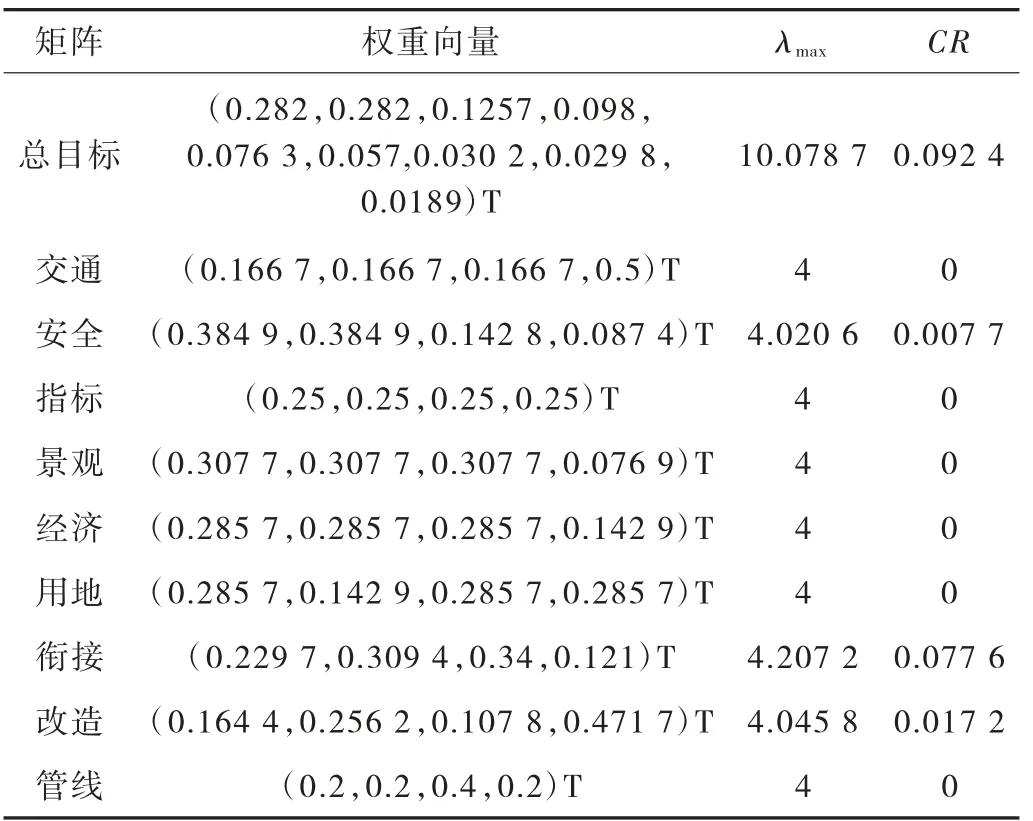
表3 判别矩阵计算结果汇总表

根据计算结果显示，所有层次单排序的一致性比例均＜0.1，通过一致性检验。

2.4 层次总排序一致性检验

通过计算，此次的层次总排序一致性检验结果为0.025 39，小于0.1，通过一致性检验。

2.5 方案比选结果

通过计算及一致性检验，此次新汇路横断面的四个方案相对优先排序如表4 所列。

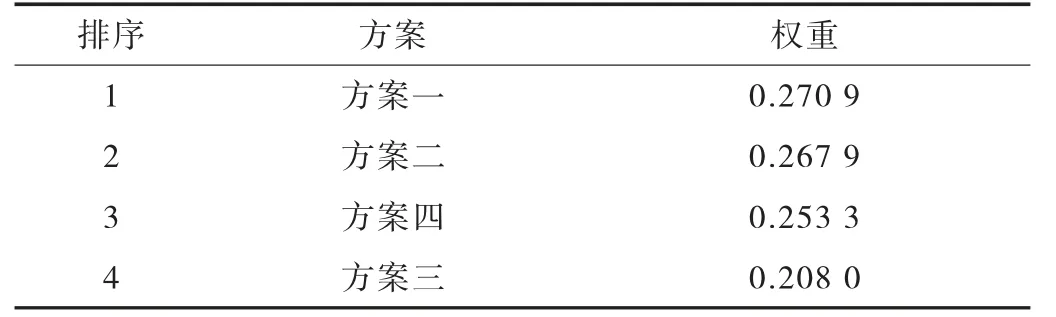
表4 方案优先排序表

根据上述权重排序结果，方案一为最佳方案。故此次新汇路横断面推荐方案为：3 m 景观带+3.5 m人行道+3.5 m 非机动车道+1.5 m 侧分带+7.5 m 机动车道+2 m 中央带+7.5 m 机动车道+1.5 m 侧分带+3.5 m 非机动车道+3.5 m 人行道+3 m 景观带=40 m规划红线宽度。

3 应用案例2：路面结构方案比选

3.1 项目背景

龙吴路位于黄浦江西岸，北起徐汇区龙华地区，南至吴泾镇，与内环、中环、外环、S32 等快速高架路相交，是一条重要的南北向的主干路，承担着大量的客货运交通。龙吴路始建成于上世纪1990 年12 月，于2001 年12 月全线改扩建竣工，2012 年对龙吴路分段进行了道路大修，并对老路路基进行了注浆加固处理，路面结构补强则采取了加罩11cm 沥青面层的方案。如今车行道沥青路面出现了大量裂缝、龟裂、沉陷及坑槽等病害，严重影响车辆的通行安全及市容市貌。

在这次大修工程中，针对路面结构的补强工作是整个设计工作的重点，该项设计在综合考虑结构强度、施工工期、交通影响等因素后，拟对如下3 种形式进行方案比选，具体如下：

方案一（刚性基层）：

4 cm SMA-13 沥青玛蹄脂碎石[SBS]

5 cm AC-20C 中粒式沥青混凝土

7 cm AC-25C 粗粒式沥青混凝土

30 cm C40 水泥混凝土（配连续钢筋网）

利用原道路路面结构

方案二（半刚性基层）：

4 cm SMA-13 沥青玛蹄脂碎石[SBS]

5 cm AC-20C 中粒式沥青混凝土

7 cm AC-25C 粗粒式沥青混凝土

38 cm 水泥稳定碎石

利用原道路路面结构

方案三（柔性基层）：

4 cm SMA-13 沥青玛蹄脂碎石[SBS]

5 cm AC-20C 中粒式沥青混凝土

7 cm AC-25C 粗粒式沥青混凝土

30 cm ATB-30 沥青稳定碎石混合料

利用原道路路面结构

3.2 路面结构方案层次结构模型

路面补强方案考虑的主要因素，按相对重要性排列如下：

（1）很重要

a. 施工可行性因素；

b. 耐久性因素；

c. 结构强度因素；

d. 道路保通影响因素；

e. 造价因素。

（2）比较重要

a. 废料外运因素；

b. 施工工期因素。

根据以上因素建立路面结构方案的层次结构模型，如图3 所示。

图3 路面结构方案层次结构模型

3.3 层次单排序一致性检验

依据路面结构方案层次结构模型构造的判别矩阵，分别计算最大特征值、特征向量及一致性比例，计算结果列于表5。

表5 判别矩阵计算结果汇总表

根据计算结果显示，所有层次单排序的一致性比例均＜0.1，通过一致性检验。

3.4 层次总排序一致性检验

通过计算，此次的层次总排序一致性检验结果为0.039，小于0.1，通过一致性检验。

3.5 方案比选结果

通过计算及一致性检验，此次龙吴路路面结构补强方案三个方案相对优先排序如表6 所列。

表6 方案优先排序表

根据上述权重排序结果，方案二为最佳方案，即选半刚性基层的补强结构方案为推荐方案。

4 结 语

本文尝试通过运用层次分析法，建立层次结构模型，构建量化的权重矩阵，将方案比选工作转为定量分析。最终通过所有方案的权重得分排序，来确定最优的推荐方案。本文通过对道路横断面方案及路面结构方案的比选为例，介绍了层次分析法在道路设计工作中的应用，以期为道路方案的设计工作提供一些有益的参考。