基于高斯混合聚类算法的西安市人工填土空间分布研究
2022-06-24刘梁石卫张晓平韩冰董欣袁琳
刘梁,石卫,张晓平,韩冰,董欣,袁琳
(1.西安市勘察测绘院,陕西 西安 710059;2.陕西省水工环地质调查中心,陕西 西安 710068;3.地质灾害防治与地质环境保护国家重点实验室(成都理工大学),四川 成都 610059;4.陕西省城市地质与地下空间工程技术研究中心,陕西 西安 710068)
城市开发过程中,一些具有特殊性质的岩土体,如人工填土、湿陷性黄土、砂土、卵砾石等,对工程建设具有较大影响,查明这类岩土体的空间分布特征,有助于做好城市规划、保障建设安全。目前,特殊岩土体的空间分布研究方法主要是根据地形、地貌及地质作用进行经验判断(西安市城市规划管理局,1998),利用地质钻孔资料进行空间插值建立三维模型进行预测(李豪,2018),以及利用遥感手段和其他相关性参数进行分析推断(郭培虹等,2010)。经验判断的方法十分依赖于研究人员对该区域的熟悉程度和经验水平;模型预测则依赖于插值方法的准确性和三维模型的精度;遥感推断与辅助参数的相关性和分析人员的技术水平关联甚密。
机器学习的主要内容是研究从数据中产生模型的算法,并将经验数据提供给这些算法,使其能够基于数据产生数学模型(周志华,2016)。机器学习是一种大数据分析方法,能够很好地利用已有数据,且在接受经验数据指导的同时降低人为因素的影响。由于地学数据割裂严重,难以形成大数据集合,因而机器学习的方法在地学领域应用较少。近年来,也有许多学者通过数据收集,开展了相关的研究,如滑坡敏感性分析及空间预测(Park Inhye et al., 2014)、土壤流失等级预测(Moller Anders Bjorn,et al.,2019)、地面沉降致因量化评价(Zhou Chaofan et al.,2019)、地下水生产潜力制图(Lee Saro et al., 2015)及滑坡易发性评价(邱维蓉等,2020)等,取得了一定的成果。机器学习中的聚类算法通常被用于对无标记训练样本进行学习,以揭示数据内在的性质和规律,为进一步的数据分析提供基础,这种方法不存在客观标准,给定一个数据集,总能从某个角度找到以往算法未覆盖的某种标准。常见的聚类算法有k均值算法(Jain,1998,2009)、学习向量量化(Kohonen,2001)和高斯混合聚类(McLachlan,2000)等。
目前常用的空间插值方法均存在主观性强、数据利用率低和通用性差的缺点。因此,笔者选用机器学习中的聚类算法来开展人工填土的分布研究。在各种聚类算法中,高斯混合聚类虽然通常被归类为聚类算法,但它本质上是一个密度估计算法,从技术角度考虑,高斯混合模型描述了数据分布的生成概率模型,它试图找到多维高斯概率分布的混合体,从而获得任意数据集最好的模型,因而更适合用作土体分布研究。
1 研究区范围及地质背景
以西安市三环内主城区约4 00 km2为研究区域,收集并整理研究区内工程地质钻孔20 793个。研究区内出露地层以新生界(Kz)为主,其中第四系厚度为600~1 000 m,对工程建设影响较大的主要地层有人工填土(杂填土、素填土)、粉质黏土、黄土状土、黄土、古土壤和砂土等。
西安市的人工填土在城区和近郊广为分布。目前所见的人工填土大多是近400~500年以来所形成的。西安市的人工填土不仅分布广泛,厚度大(多在3~10 m,局部地区最大厚度可达十几米),土层产状和厚度在平面上变化十分迅速,而且性质非常复杂。就其物质组成及工程性质而言,可将西安市的人工填土分为杂填土和素填土2类。西安市的杂填土颜色多而杂,结构疏松,物质组成是以各个时期的建筑垃圾为主,部分地区的杂填土夹有少量植物根系,土的均匀性极差,工程建设中不能直接选作天然地基的持力层。在西安市主城区,素填土一般伏于杂填土之下,在城郊则多直接出露地表。西安市的素填土多由黏性土组成,一般含有少量砖、瓦块碎屑等,具有大孔结构和轻微湿陷性,可以作为一些次要或临时性建筑的地基持力层,对二级建筑及以上建筑一般均应进行地基的加固处理。
2 空间分布特征的研究方法
2.1 高斯混合聚类
高斯混合聚类(Mixture of Gaussian)采用概率模型来表达聚类原型,在多元高斯分布定义中,对n维样本空间χ中的随机向量x,若x服从高斯分布,其概率密度函数如下。
(1)
其中μ是n维均值向量,∑是n×n的协方差矩阵。由式(1)可以看出,高斯分布完全由均值向量μ和协方差矩阵∑这2个参数确定。为了明确显示高斯分布与相应参数的依赖关系,将概率密度函数记为p(x)|μ,∑)。因此,笔者可以将高斯混合分布定义如式(2)
(2)
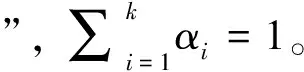
假设样本的生成过程由高斯混合分布给出:首先,根据α1,α2,…,αk定义的先验分布选择高斯混合成分,其中αi为选择第i个混合成分的概率,然后根据被选择的混合成分的概率密度函数进行采样,从而生成相应的样本。
若训练集D={x1,x2,…,xm}由上述过程生成,令随机变量zj∈{1,2,…,k}表示生成样本xj的高斯混合成分,其取值未知。显然,zj的先验概率P(zj=i)对应于αi(i=1,2,…,k)。根据贝叶斯定理,zj的后验分布对应于式(3)
pM(zj=i|xj)=
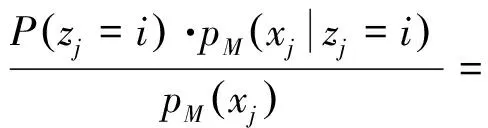
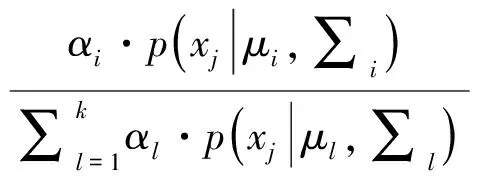
(3)
换言之,pM(zj=i|xj)给出了样本xj由第i个高斯混合成分生成的后验概率。为方便叙述,将其简记为γji(i=1,2,…,k)。
当高斯混合分布(2)已知时,高斯混合聚类将把样本集D划分为k个簇C={C1,C2,…,Ck},每个样本xj的簇标记λj如下确定。
λj=argmaxi∈{1,2,…,k}γji
(4)
因此,从原型聚类的角度来看,高斯混合聚类是采用概率模型(高斯分布)对原型进行刻画,簇划分则由原型对应后验概率确定。
(5)
即每个高斯成分的混合系数由样本属于该成分的平均后验概率确定。
由上述分析即可获得高斯混合模型的EM算法,即在每步迭代中,先根据当前参数来计算每个样本属于每个高斯成分的后验概率γji(E步),再更新模型参数{αi,μi,∑i|1≤i≤k}(M步)。
高斯混合聚类算法描述见图1。算法第1行对高斯混合分布的模型参数进行初始化,然后,在第2~12行基于EM算法对模型参数进行迭代更新。若EM算法的停止条件满足(例如已达到最大迭代轮数,或似然函数LL(D)增长很少甚至不再增长),则在第14~17行根据高斯混合分布确定簇划分,在第18行返回最终结果。

图1 高斯混合聚类算法图
2.2 聚类算法的检验
高斯混合模型采用似然函数作为目标函数,当训练数据足够多时,可以不断提高模型精度,但是以提高模型复杂度为代价的,同时带来一个机器学习中非常普遍的问题——过拟合。所以,模型选择问题在模型复杂度与模型对数据集描述能力(即似然函数)之间寻求最佳平衡。人们提出许多信息准则,通过加入模型复杂度的惩罚项来避免过拟合问题,常用的2个模型选择方法——赤池信息准则(Akaike Information Criterion,AIC)和贝叶斯信息准则(Bayesian Information Criterion,BIC)。
2.2.1 赤池信息准则
AIC是衡量统计模型拟合优良性的一种标准,由日本统计学家赤池弘次在1974年提出,它建立在熵的概念上,提供了权衡估计模型复杂度和拟合数据优良性的标准。
通常情况下,它是拟合精度和参数未知个数的加权函数,AIC定义为:
AIC=2k-2ln(L)
(6)
其中,k是参数的数量,L是似然函数。当在2个模型之间存在着相当大的差异时,这个差异出现于式(6)的第二项,而当第二项不出现显著性差异时,第一项起作用,从而参数个数少的模型是好的模型。
假设模型的误差服从独立正态分布,让n为观察数,RSS为剩余平方和,那么AIC变为:
AIC=2k+nln(RSS/n)
(7)
一般而言,当模型复杂度提高(k增大)时,似然函数L也会增大,从而使AIC变小,但是k过大时,似然函数增速减缓,导致AIC增大,模型过于复杂容易造成过拟合现象。目标是选取AIC最小的模型,AIC不仅要提高模型拟合度(极大似然),而且引入了惩罚项,使模型参数尽可能少,有助于降低过拟合的可能性。可见AIC准则有效且合理地控制了参数的维数k。赤池信息准则的方法是寻找可以最好地解释数据但包含最少自由参数的模型。
2.2.2 贝叶斯信息准则
贝叶斯信息准则与AIC相似,用于模型选择,1978年由Schwarz提出。训练模型时,增加参数数量,也就是增加模型复杂度,会增大似然函数,但是也会导致过拟合现象。针对该问题,AIC和BIC均引入了与模型参数个数相关的惩罚项,BIC的惩罚项比AIC的大,考虑了样本数量,样本数量过多时,可有效防止模型精度过高造成的模型复杂度过高。
BIC=kln(n)-2ln(L)
(8)
其中,k为模型参数个数,n为样本数量,L为似然函数。式(8)中第一项为惩罚项,在维数过大且训练样本数据相对较少的情况下,可以有效避免出现维度灾难现象。
3 西安市人工填土空间分布研究
3.1 数据准备
在研究区范围内,钻孔数据集中包含杂填土的钻孔共有13 687个,包含素填土的钻孔共有7 106个。区内杂填土层底埋深在0.1~24 m,素填土层底埋深在0.1~16.5 m。按照城市地下空间开发层次将人工填土数据划分为厚度小于3 m、厚度介于3~10 m、厚度大于3 m 3种分类,分别进行聚类计算及制图。
土体分布研究中常常使用土体平面坐标及层厚作为分布计算的属性。土体平面坐标(x坐标、y坐标)及层厚属性均为连续属性,可以直接参与聚类任务的距离计算。在本次研究中,笔者增加了土体时代成因属性参与到聚类任务中,以优化聚类过程,从而得到更贴切土体分布要求的聚类结果。土体的时代成因属于离散属性,在其定义域上是有限个取值。在距离计算时,土体的地质时代属性为有序属性,而成因属性则为无序属性。因此,直接使用土体地质年代作为其标准化结果(Q4->4;Q3->3;Q2->2;Q1->1),同时使用一组连续正整数对土体成因进行编码处理(表1)。

表1 土体成因编码表
3.2 聚类计算
将准备好的数据导入事先编制好的计算程序中,利用前述的高斯混合模型进行聚类计算。输入的训练集数据为一系列5维数组,每单个数据包含了该钻孔的x坐标、y坐标、层厚、地质时代和成因属性。
聚类计算首先要进行试算以确定最优的聚类簇数,即先假定聚类簇数n,再分别计算当聚类簇数为n时,赤池信息准则AIC值及贝叶斯信息准则BIC值,比较各聚类簇数对应的AIC和BIC值,选择合适的聚类簇数为最终计算参数。如图2所示,笔者首先从聚类簇数n=1时开始试算,杂填土的试算终点为n=280,素填土的试算终点为n=200,试算步长为1。由于聚类簇数过小时,杂填土聚类计算的AIC和BIC值过大,因此,为了曲线美观便于观察,将杂填土的计算从聚类簇数n=50开始绘制分析曲线。从杂填土聚类簇数分析曲线(图2a)中可以看出,杂填土数据的AIC值程持续下降趋势,即聚类簇数越大,赤池信息准则模型评价越精确,在n≥140后,曲线下降趋于平缓。而其BIC值有明显的“底部”,即120≤n≤140时,BIC值更小,表明n在这个区间范围内取值时,贝叶斯信息准则模型评价最精确。从素填土聚类簇数分析曲线(图2b)中可以看出,素填土数据的AIC值程持续下降趋势,即聚类簇数越大,赤池信息准则模型评价越精确,在n≥140后,曲线下降趋于平缓。其BIC值与AIC值趋势相似,n≥120后曲线趋于平缓,表明n在这个区间范围内取值时,贝叶斯信息准则模型评价最精确。综合2种评价准则,取杂填土和素填土的聚类簇数n=140。
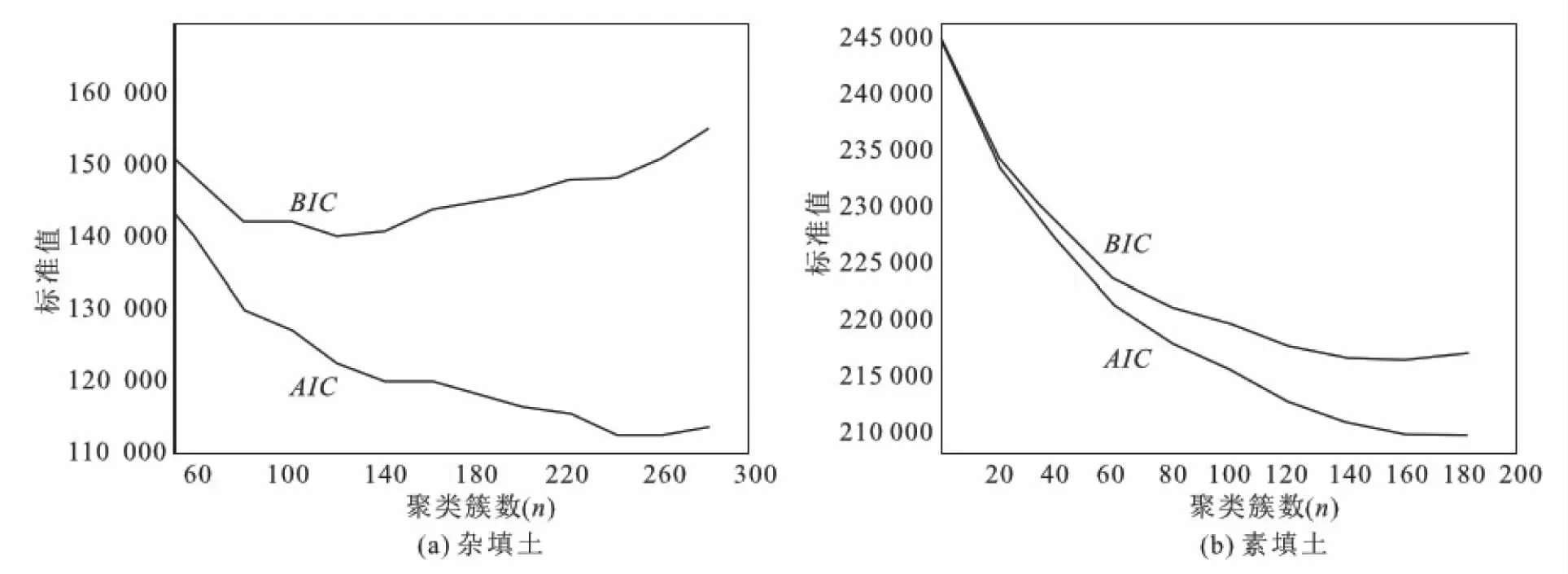
图2 人工填土聚类簇数分析曲线图
3.3 分布特征
研究区人工填土分布广泛,厚度多在3~10 m,局部地区最大厚度可达十几米,土层产状和厚度在平面上变化迅速,性质较为复杂,主要可分为杂填土和素填土2类。杂填土颜色多且杂,结构疏松,物质组成是以各个时期的建筑垃圾为主,土的均匀性极差,工程建设中不能直接选作天然地基的持力层。研究区内杂填土广泛分布,埋深多在3 m以内,部分地区埋深可达3~10 m,极少数区域杂填土层底深度达到10 m以上。研究区内素填土与杂填土相似,均广泛分布于城区各处,埋深多在3 m以内,部分地区埋深可达3~10 m,极少数区域素填土层底深度达到10 m以上(图3)。
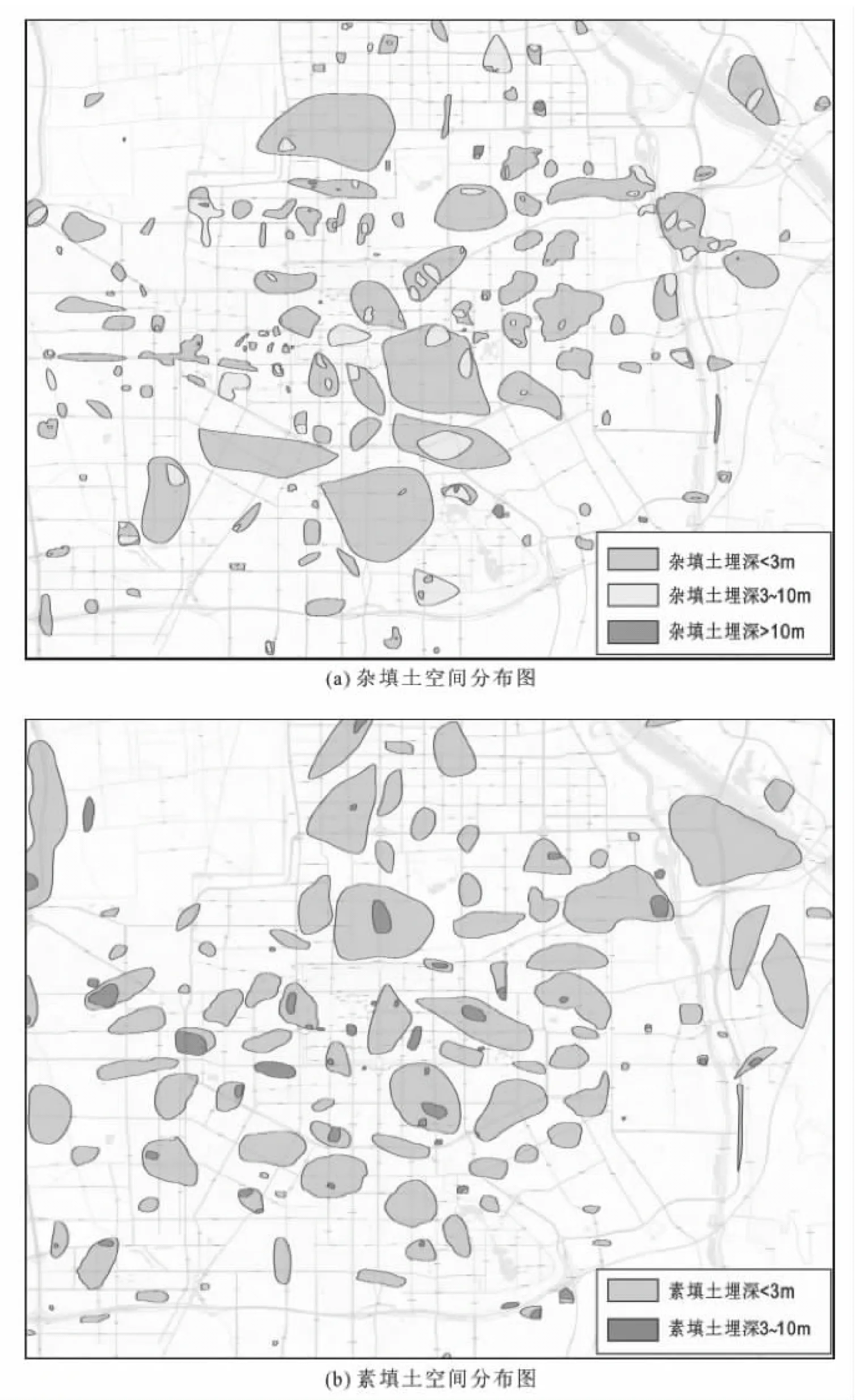
图3 西安市人工填土空间分布图
4 结论
(1)高斯混合模型采用似然函数作为目标函数,当训练数据足够多时,可以不断提高模型精度,能够准确而快速的表达土体的分布特征,但需要借助赤池信息准则和贝叶斯信息准则来避免出现模型过拟合的问题。
(2)赤池信息准则(AIC)及贝叶斯信息准则(BIC)检验试算结果表明,在聚类簇数n=140时,高斯混合聚类模型能更为准确的评价西安市人工填土的空间分布状态。
(3)西安市主城区内杂填土广泛分布,埋深多在3 m以内,部分地区埋深可达3~10 m,极少数区域杂填土层底深度达到10 m以上,主要分布于主城区大部分区域,浐灞河沿线、西绕城、南绕城也有零星分布。
(4)西安市主城区内素填土广泛分布于城区各处,埋深多在3 m以内,部分地区埋深可达3~10 m,极少数区域素填土层底深度达到10 m以上。浐灞河三角、浐河沿线、西绕城沿线、鱼化寨区域有成片分布。
