基于四面体单元的三维裂纹自动化建模
2022-06-24高文王生楠
高文,王生楠
(西北工业大学航空学院,西安 710072)
0 引言
工程结构由于材料夹杂或服役等原因不可避免地存在缺陷或裂纹,这些缺陷或裂纹在疲劳载荷的作用下逐渐扩展最终导致结构发生断裂。据统计,大约60%的结构失效是由疲劳裂纹扩展引起的,因此,需要对含裂纹结构的安全性进行量化分析。在线性弹性断裂力学(Linear Elastic Fracture Mechanics,简称LEFM)范围内,应力强度因子(Stress Intensity Factors,简称SIFs)用来表征裂纹尖端附近应力场强度,是研究裂纹起裂和扩展的关键因素。但只有少数形式简单的裂纹可以通过试验或解析的方式获得应力强度因子解,对于形式复杂的裂纹问题,不可避免地要使用有限差分法、有限元法、边界元法等数值方法来求解。在这些方法中,有限元法由于其较高的求解效率和可以模拟任意复杂几何形状而在工程界占据主导地位。

本文以二次四面体单元VCCM法为基础,对应用四面体单元进行三维裂纹有限元建模方法进行研究,对VCCM法计算断裂参数的影响因素进行分析,裂纹建模过程需要繁琐的手工操作,全自动化建模也是本文的研究重点。
1 虚拟裂纹闭合法
1.1 二次四面体单元的VCCM法计算式
由VCCM法的理论可知,在裂纹的虚拟扩展面上需要有单元面片存在以获得计算所需的节点力,且裂纹前缘两侧的面片宽度需相等。四面体单元的面是三角形,典型的裂纹前缘二次四面体单元分布示意图如图1所示。裂纹前缘的三角形单元面片分为两种:一种是三角面片的一条边位于裂纹前缘,记为;另一种是三角面片的一个顶点位于裂纹前缘,记为,Δ为单元宽度,如图2所示。面片和上的计算式如式(1)~式(2)所示。


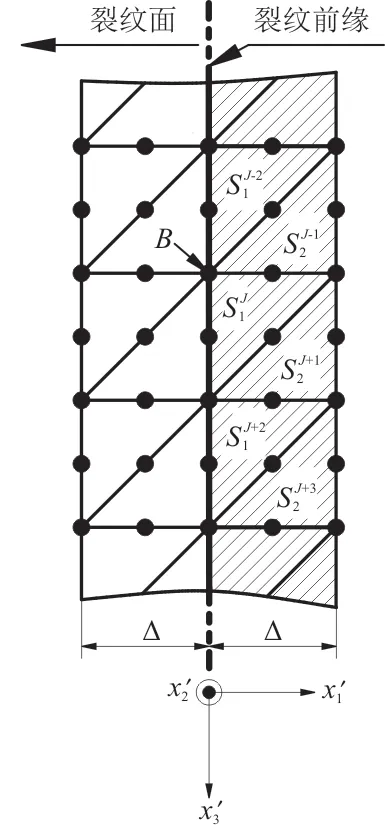
图1 典型裂纹前缘单元分布示意图Fig.1 Element face arrangements across the crack front
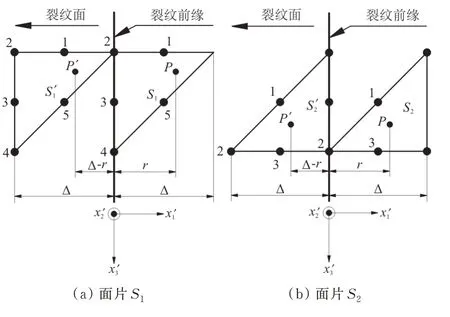
图2 裂纹前缘两种单元面片示意图Fig.2 Two kinds of arrangements of paring finite element faces
线弹性断裂力学范围内,和的关系如式(3)所示。

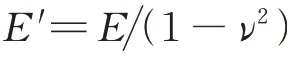
由此可得单元面片S(=1,2)对应的SIFs计算式:
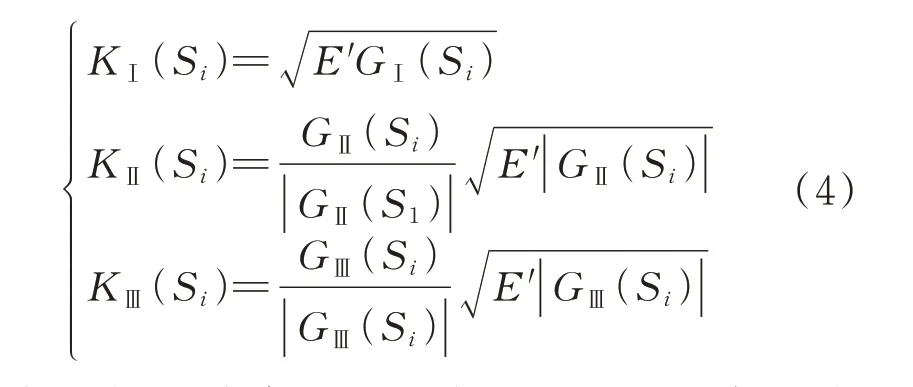
应变能释放率总是假设为正,注意到式(1)、式(2)和式(4)中和可能为负,此处的正负号表示裂尖局部坐标系下裂纹的变形方向。
1.2 节点力和裂纹张开位移的计算
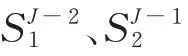

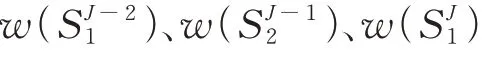


裂纹张开位移的计算较简单,裂纹面上表面的节点位移减去下表面对应节点的位移,可得全局坐标系下的裂纹张开位移,再将其转换成裂尖局部坐标系下的位移分量,即可得Ⅰ、Ⅱ和Ⅲ型对应的裂纹张开位移。
2 三维裂纹自动化建模
应用ABAQUS软件分析裂纹问题的步骤包括:裂纹几何特征创建,材料属性赋值,分析步创建,裂纹属性赋值,创建边界条件和载荷施加,网格划分,定义输出,提交计算,断裂参数计算及结果保存等,这个过程需要非常繁琐的手工操作。ABAQUS软件提供了丰富的二次开发接口,所有在ABAQUS/CAE中实现的前处理和后处理均可通过Python程序实现自动化操作。本文以二次四面体单元VCCM法为基础,应用Python编程语言,结合开源科学计算库NumPy和SciPy,采用面向对象的程序设计技术,开发了三维裂纹分析程序包。该程序包由一系列函数、类和模块组成,其工作流程和在ABAQUS/CAE中分析裂纹问题的工作流程一致。上述裂纹分析步骤通过调用相应的函数或实例化相应的类来完成,各建模步骤需要的参数通过不同的接口文件给定。
2.1 裂纹几何特征创建
FRANC3D软件通过其特有的“裂纹模板”功能来完成裂纹前缘单元布置和裂纹快速插入。ZENCRACK软件通过“Crack-Block”技术引入不 同 形 式 的 裂 纹。J.C.Sobotka等提 出 在ABAQUS软件上通过Python语言二次开发生成椭圆裂纹前缘网格和裂纹快速插入的方法。上述技术和方法的目的有两个:一是在裂纹前缘生成高质量单元以提高断裂参数计算精度;二是在待分析结构上快速引入裂纹。本文通过显式创建裂纹前缘单元面片、布种控制单元分布来完成基于二次四面体单元VCCM法的三维裂纹建模,以此为基础开发参数化裂纹模板库,用于不同形式、不同尺寸的裂纹几何特征的快速引入。
待分析结构中引入裂纹几何特征可分为三步:①读取裂纹定义文件里的裂纹形式、尺寸、裂纹前缘单元数量、单元宽度、裂纹插入位置和方位等参数;②根据第①步中的裂纹参数创建裂纹几何部件;③根据第①步中的裂纹位置参数通过平移、旋转等操作,将裂纹部件移动至指定位置和待分析结构进行切割、合并等几何布尔运算,完成裂纹几何特征的引入。椭圆裂纹是一种非常重要的裂纹形式,在飞机结构的损伤容限评定中,对于结构内部、表面、孔边等部位的初始损伤通常用椭圆/圆形裂纹、二分之一椭圆/圆形裂纹、四分之一椭圆/圆形角裂纹来表示。本文以椭圆裂纹为例来说明参数化裂纹模板的实现过程。
设为全局坐标系,坐标系原点坐标为(0,0,0),基底向量为=(1,0,0),=(0,1,0),=(0,0,1),裂纹初始位置位于全局坐标系平面上,椭圆中心位于坐标系原点,裂纹面坐标系记为,如图3(a)所示。裂纹前缘上一点的坐标(,,)可由式(7)得到:

式中:,为椭圆的短半轴和长半轴尺寸;为点椭圆离心角,∈(-π,π]。


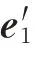
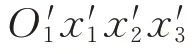

图3 椭圆裂纹前缘面片顶点Fig.3 Vertices of element faces across the crack front
由此,对椭圆上的离散点序列(,,,…)的每一个点执行同样的操作,可得位于裂纹面上的点序列(,,,…)和位于裂纹虚拟扩展面上的点序列(,,,…)的坐标,对这三组点进行编号,然后将这三组点按逆时针连接形成裂纹前缘三角面片,同时对面片进行编号并记录面片和点的拓扑连接关系,然后在ABAQUS中根据前面得到的点和三角面片连接关系及点坐标创建裂纹几何部件,如图4所示。需注意,裂纹前缘三角面片应具有良好的形状以避免在后续的模型网格生成中产生低质量四面体单元。
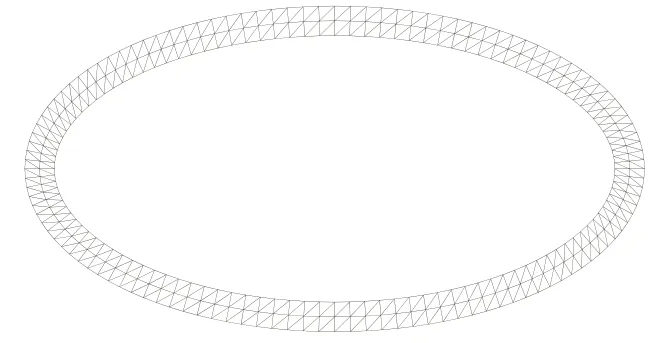
图4 椭圆裂纹模板Fig.4 Elliptical crack front template
2.2 裂纹插入及裂纹相关数据信息
裂纹几何部件创建完成后,根据裂纹定义接口文件里的裂纹位置、方位等信息,在ABAQUS软件的Assembly模块里,通过平移、旋转等操作将裂纹部件放置到指定位置,同时计算旋转、平移操作后的裂纹前缘三角面片顶点的坐标,然后和待分析结构件进行切割、合并等几何布尔运算完成裂纹几何特征的创建。对于表面裂纹或穿透裂纹,由于裂纹前缘三角面片是预先产生的,布尔运算后可能会在自由表面附近产生不规则的、影响后续网格划分的小边和小面,需要进一步做小面删除、短边合并、新面添加等操作,完成后对裂纹前缘三角面片顶点坐标、面片编号、面片面积等数据信息进行更新。
裂纹平面初始位置位于全局坐标系的平面上,裂纹面局部坐标系和全局坐标系重合。一个空间坐标系可以用另一个参考坐标系的三次空间旋转来表达,由此可知,空间任意位置的裂纹可通过将初始裂纹最多旋转三次来实现。假设裂纹插入位置的坐标为(t,t,t),绕裂纹面局部坐标系轴、轴、轴依次旋转、和,则对应的坐标转换矩阵为
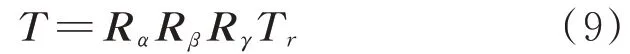
其中,R、R、R、T的定义如下:

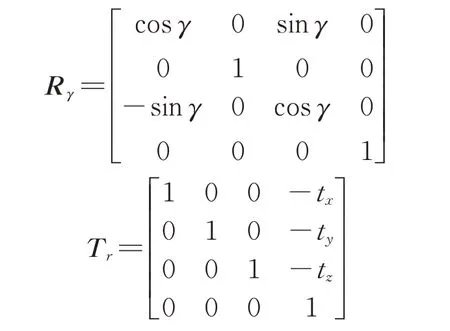
由此,(,,)为某点的初始坐标,则经旋转平移后的坐标(,,)可由式(10)计算得到。
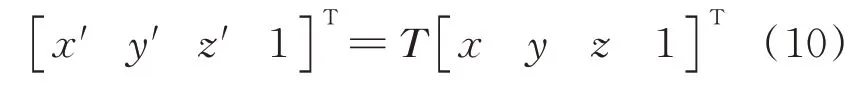
2.3 网格划分
四面体单元可以方便的自动化生成,在有限元软件ABAQUS中对模型进行网格划分的步骤主要包括布种、网格生成技术和算法指定、单元形状和类型选择、单元尺寸增长比选择等。布种包括全模型布种和局部边或面布种,两者分别从总体和局部描述了模型网格密度。读取网格设置接口文件里的全模型布种尺寸和局部边布种尺寸及边的查找坐标,完成全局布种和局部边的布种,裂纹前缘三角面片的每条边上强制布置一个单元,单元类型设定为二次四面体单元(C3D10),网格生成技术为自由网格划分,算法选择默认网格生成算法。在关心部位的网格密度足够的情况下,单元尺寸增长比可以有效控制模型总体单元规模。根据经验,其他网格参数保持不变的情况下,单元尺寸增长比取1.0时生成的模型四面体单元数量是取1.5时生成单元数量的3~4倍。单元尺寸增长比设置过小会导致网格规模偏大,过大则可能会产生低质量单元进而影响计算结果。为了兼顾网格质量和计算效率,通过迭代的方式决定单元尺寸增长比的大小。具体思路如下:网格划分其余设置不变,单元尺寸增长初值设为1.5,每次迭代初值减0.1直至1.0停止循环,每次循环对模型进行一次网格划分,划分完成后对网格质量进行评估,如果该次循环没有警告单元,跳出循环,模型网格划分完成;如果迭代至循环结束每一次循环均有警告单元,取警告单元数量最少的网格为最终的模型网格。
2.4 节点集合和单元集合创建

由上述分析可知,计算所需的节点力需要用裂纹面上方的单元来计算,裂纹张开位移需要裂纹上表面位移节点和下表面对应节点的位移差来计算,此过程均需判断四面体单元和面片的位置关系。和节点力节点(图2中面片上的节点1,2,3,4,5和面片上的节点1,2,3)关联的四面体单元可分为3种情况:①四面体单元一个顶点和三角面片的顶点重合;②四面体单元的一条单元边和三角面片的边重合;③四面体单元的一个单元面和三角面片重合。如果根据四面体单元的顶点坐标去判断四面体单元和三角面片的位置关系,需要进行较为繁琐的情况甄别和顶点选取,而四面体单元的内切球球心必定和四面体单元位于面片的同一侧,本文通过判断四面体内切球心和三角面片的位置来确定四面体单元和面片的位置关系。
点和面的位置关系可以通过判断该点和面内三点坐标组成的行列式的符号来判定。设三维空间点,,,,坐标分别为(a,a,a),(b,b,b),(c,c,c),(d,d,d),定义行列式:

式(11)的几何意义为,,三点逆时针排列,当det(,,,)<0时,点位于过、三点平面的上方;当det(,,,)>0时,点位于过、三点平面的下方。
由此可以得出四面体单元和三角面片的位置关系判断方法:①根据四面体单元的顶点坐标计算四面体单元的内切球球心坐标;②将三角面片的三个顶点坐标和四面体球心坐标带入式(11),根据行列式的符号即可得四面体单元和面片的位置关系。
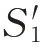
以面片为例来说明载荷面片相关数据信息的建立过程:①根据三角面片的顶点坐标获得载荷节点(图2中面片上1,2,3,4,5节点)的坐标;②根据坐标查找网格节点,获得网格节点编号,同时计算该节点的载荷分配系数;③根据单元和节点连接关系获得包含该节点的所有四面体单元;④根据四面体单元和三角面片位置判断方法对第③步中获得的四面体单元进行过滤,保留位于面片上方的单元。
对每一个位移面片和载荷面片按照上述方法建立计算所需的数据信息,所有的位移面片上的位移节点取并集得到节点集合Set-NodesU,所有载荷面片上节点力计算相关的单元取并集得到单元集合Set-ElemsF,这两个集合将用于定义输出位移和节点力。
2.5 输出定义
模型创建完成后,调用ABAQUS/Standard生成模型的*.inp文件,通过修改*.inp文件定义输出计算所需的相关节点的位移和节点力至*.dat文件。定义输出节点力和位移的命令如下:
*EL PRINT,ELSET=Set-ElemsF
NFORC
*NODE PRINT,NSET=Set-NodesU
U
2.6 其他步骤
材料属性赋值:读取材料属性定义文件里的材料属性参数,调用函数完成模型材料属性赋值。
裂纹属性赋值:有限元法以无应力面的形式来模拟裂纹,ABAQUS软件里通过给面片或边赋Seam属性来定义裂纹,生成网格时在Seam面片上产生重叠的重复节点,在分析过程中节点分离来模拟裂纹受载。根据存储的裂纹面相关面片坐标信息,对几何面片赋Seam属性。
边界条件和载荷:根据载荷和边界条件定义文件里的相关参数,完成载荷施加和边界条件创建。
提交计算:模型*.inp文件修改完成后,调用函数提交计算。
断裂参数计算及结果保存:有限元模型求解完成后,读取输出文件*.dat里相关节点的位移和节点力,根据前述的VCCM法理论并应用光顺技术计算裂纹前缘SIFs,计算完成后将计算结果和对应位置的坐标、局部坐标系等相关信息保存至文件以供下一步操作。
3 数值算例
通过数值算例对VCCM法计算断裂参数的影响因素进行分析,在此基础上,对表面裂纹的SIFs进行计算。
3.1 VCCM法影响因素分析
应用四面体单元计算得到的断裂参数沿裂纹前缘 会出现 震荡,H.Okada等采用 光顺技术来解决这一问题。光顺技术的核心思想是以一小段裂纹前缘上的均值来取代单个面片的值。本文以Ⅰ型和复合型内埋椭圆裂纹为例对光顺面片数量、单元宽度Δ以及单元尺寸对VCCM法计算断裂参数的影响进行分析。
3.1.1 光顺面片数量
H.Okada等的研究表明,随着变大,沿裂纹前缘计算结果波动变小,但当进一步取至21时,裂纹前缘曲率变化大的位置的计算结果和理论解的相对误差扩大。原因是值越大参与光顺的面片覆盖的裂纹段就越长,裂纹前缘曲率变化大的裂纹段上变化比较大,而光顺算法的核心是取均值,由此导致数值计算结果和真实值出现偏差。因此,值的选择倾向于相对小的值以避免光顺范围内的裂纹段上结果有明显波动,文献[11]给出的建议是取5~15。然而,当裂纹前缘某段曲率变化很大时,即使取相对小的值也不能解决上述问题。以文献[11]中的Ⅰ型内埋椭圆裂纹算例为例,取9,当取较大值时,VCCM法计算结果和理论解最大相对误差均小于2%;当取0.2时,VCCM法的计算结果和理论解的最大相对误差扩大至3.9%。文献[11]没有给出取更小值时VCCM法计算结果和理论解的对比,但有理由相信两者的误差会更大。该问题其中一个改善方法是沿曲线裂纹前缘非等尺寸布置单元,曲率大的地方单元尺寸适当减小,如图4所示。由此在特定的值下,裂纹前缘曲率大的地方参与光顺计算的面片覆盖的裂纹段减小,该裂纹段上的波动范围也会相对减小。
承受远端拉伸载荷内埋斜置椭圆裂纹示意图如图5所示,当=0时,裂纹尖端承受Ⅰ型载荷。模型尺寸=10,可视为无限大体;取0,裂纹前缘单元数取360,单元宽度Δ取裂纹前缘 平 均 单 元 尺 寸/,为 裂 纹 前 缘 长度,/分别取0.1,0.2,0.4,0.5,0.6,0.8,1.0,模型单元数为113 590~173 198,节点数为159 272~239 448,/0.5时内埋椭圆裂纹有限元网格如图6所示。需注意,大多数情况下,Δ取都能获得形状良好的裂纹前缘三角面片,但当/取很小的值(比如0.1)时,有可能会产生自相交而导致建模失败,此时,可通过改变裂纹前缘单元数或减小单元宽度Δ来解决,这一过程由程序自动完成。

图5 远端拉伸内埋斜置椭圆裂纹示意图Fig.5 The problem of embedded elliptical crack

图6 a/c=0.5时内埋椭圆裂纹有限元网格Fig.6 A typical finite element model for the embedded elliptical crack problem for the case of a/c=0.5
=0.5,取不 同 值 时VCCM法 计 算结 果和理论解的对比如表1所示,为了更清晰地展示取不同对VCCM法的影响,表1中的误差分析保留三位小数,后续的误差分析均保留两位小数。

表1 a/c=0.5时Ne取不同值VCCM法计算结果误差分析Table 1 Summary of error for modeⅠembedded elliptical crack with different Ne computing SIFs
从表1可以看出:=2时,计算结果和理论解的平均误差和最大误差分别为0.507%和1.639%,但波动明显,如图7(a)所示;随着进一步变大,计算结果波动性变小,和理论解的相对误差变小,当取至30时,计算结果和理论解依然吻合非常好,平均误差为0.145%,最大相对误差为0.360%,如图7(b)所示,并没有出现文献[11]中误差明显扩大的现象,说明在当前的裂纹前缘网格布置下(如图4和图6所示),VCCM法计算断裂参数的稳定性有提高。综合各方面因素,本文后续的分析中,取10。

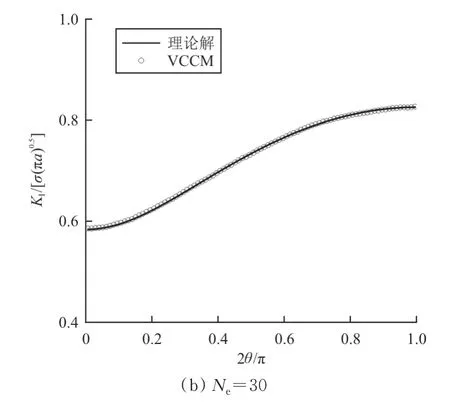
图7 Ne取不同值VCCM法计算结果和理论解的对比Fig.7 The distributions of the stress intensity factor along the crack front for different Ne
/取不同值时VCCM法计算结果和理论解的误差分析如表2所示,可以 看出:当/≥0.4时,VCCM法计算结果和理论解吻合非常好,平均误差小于0.24%,最大误差小于0.71%;随着/变小,误差稍有扩大,但依然和理论解吻合很好,当=0.2和=0.1时,平均误差分别为0.53%和1.64%,最大相对误差分别为1.02%和3.03%。误差变大的原因是小的值靠近长轴的裂纹前缘单元尺寸小,单元宽度取定值导致的单元形状不够优良。
表2 Ⅰ型内埋椭圆裂纹误差分析Table 2 Summary of error for modeⅠembedded elliptical crack with fixed-width element faces
3.1.2 单元宽度
由前面的分析可以看出,当取很小的值,比如0.1时,VCCM法的计算结果和理论解的误差稍有扩大,原因是裂纹前缘的单元形状不够优良。本节裂纹前缘面片采用变宽度,单元宽度等于单元尺寸,如图8所示。模型尺寸=10,裂纹前缘单元数取360,/分别取0.1,0.2,0.4,0.5,0.6,0.8,1.0,模 型 单 元 数 为94 414~131 068,节点数为133 788~183 942。VCCM法计算结果和理论解的误差分析如表3所示,可以看出:/=0.1时,相较于裂纹前缘单元宽度取定值,计算结果和理论解的平均误差和最大误差均有改善;/=0.2时,平均误差有小幅改善,但最大相对误差稍有扩大;/≥0.4时,两种裂纹前缘单元布置的数值计算结果很接近。
两种裂纹前缘单元布置的计算结果说明单元宽度对VCCM法的影响很小,裂纹前缘单元具有良好的形状即可获得非常好的结果。实际上,对于真实裂纹,小的值对应的裂纹形状是不稳定的,在疲劳载荷的作用下,裂纹前缘陡峭的地方随着裂纹的扩展会快速变得平缓。
图8 变宽度单元面片的椭圆裂纹模板Fig.8 Elliptical crack front template with changing element width
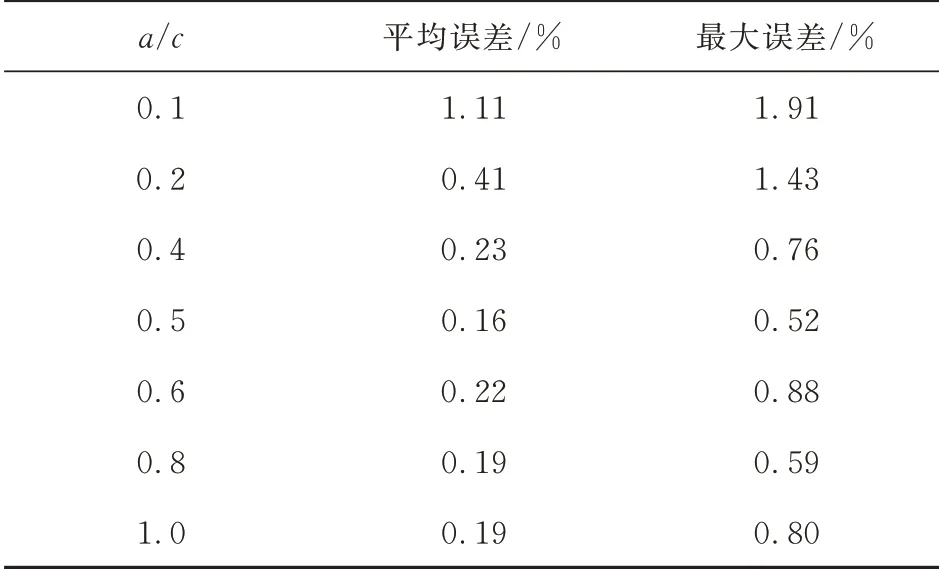
表3 Ⅰ型内埋椭圆裂纹误差分析Table 3 Summary of error for modeⅠembedded elliptical crack with changing-width element faces
3.1.3 单元尺寸
本节对复合型内埋椭圆裂纹的SIFs进行计算并和理论解进行对比,研究单元尺寸对VCCM法计算断裂参数的影响。模型尺寸=10,模型尺寸大于10倍裂纹尺寸,可视为无限大体,取π/4,裂 纹 前 缘 单 元 数分 别 取180和360,分别取0.4,0.6,0.8,裂纹前缘单元宽度Δ取定值。取180时,模型单元数为56 644~65 957,节点数为82 847~95 730;取360时,模型单元数为87 619~128 285,节点数为125 930~180 278。复合型内埋椭圆裂纹误差分析如表4所示。

表4 复合型内埋椭圆裂纹误差分析Table 4 Summary of error for mixed mode embedded elliptical crack
从表4可以看出:随着裂纹前缘网格加密,VCCM法计算的Ⅰ、Ⅱ、Ⅲ型应力强度因子、、和理论解的平均误差均减小,、和理论解最大误差同样减小,和理论解的最大误差反而有小幅增大。说明随着网格加密,裂纹前缘上绝大多数位置的数值计算结果和理论解的误差均减小,个别位置的值和理论解误差稍有扩大。=180时,VCCM法计算的、、和理论解的平均误差为0.24%~0.35%、0.56%~1.21%、0.47%~0.68%;=360时,VCCM法计算的、、和理论解平均误差为0.23%~0.27%、0.36%~0.57%、0.27%~0.32%。表明两种网格均得到了很好的结果,同时也说明单元尺寸对VCCM法的影响有限。
3.2 Ⅰ型表面裂纹应力强度因子计算

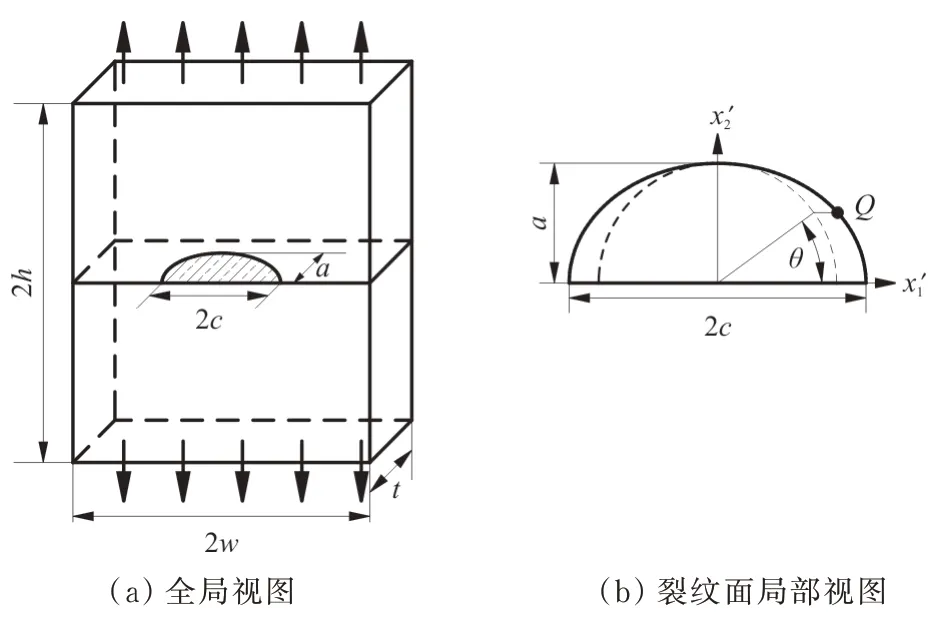
图9 有限宽板表面裂纹Fig.9 The problem of semi-elliptical surface crack

图10 a/c分别取0.6和0.8时裂纹前缘应力强度因子分布Fig.10 The distributions of the SIFs for a/c being 0.6 and 0.8
4 结论
(1)通过显式创建裂纹前缘单元面片结合布种控制单元分布实现了基于二次四面体单元VCCM法的三维裂纹建模。全模型采用常规四面体单元显著简化了建模流程,提高了三维裂纹自动化建模的稳定性和鲁棒性。
(2)本文开发了基于二次四面体单元VCCM法的参数化三维裂纹分析程序包,实现了三维裂纹从建模到断裂参数计算的全流程自动化,有效提升了三维裂纹问题的分析效率。
(3)单元宽度和单元尺寸对二次四面体单元VCCM法影响有限,数值算例结果和文献结果一致性良好。
(4)本文的建模方法同样可用于其他有限元软件的三维裂纹全自动化建模。此外,本文的程序包可用于三维裂纹疲劳扩展的全自动化数值模拟。
