前缘下垂结合内吹式襟翼失速特性研究
2022-06-24何萌张刘赵垒李昌
何萌,张刘,赵垒,李昌
(中国空气动力研究与发展中心低速空气动力研究所,绵阳 621000)
0 引言
飞行器起降性能是飞机设计的关键因素,当前运输机一般需要机场有较长的跑道进行起降,限制了小型机场的使用,而短距起降飞机能够充分利用所有机场以缓解机场拥挤。德国宇航中心正在研究一种新型的支线飞机SFB880,主要设计目标之一是具有短距起降能力。美国空军针对军用运输机的设计提出了“速度机敏(Speed Agile)”概念,要求运输机需同时满足高亚声速巡航性能(具有较高的0.8巡航效率)和超短距起降能力。因此对增升装置提出了更高的要求,而传统机械式增升装置难以满足,动力增升概念为复杂襟翼系统的替代提供了可能。其中环量控制翼型(CCA)是利用柯恩达效应(Coanda Effect),即射流中的压强与气流绕曲面的离心力平衡,使射流依附于曲面表面流动,改变气流方向,可有效增加翼型的环量和升力。
内吹式襟翼是环量控制翼型的典型应用,将发动机的高压气流通过管道引导到襟翼前缘,增加襟翼表面气流动量。巡航时襟翼恢复为机翼的尖后缘,可减小巡航阻力,且没有缝道流动,降低飞机的噪声水平。国内外针对内吹式襟翼设计做了很多研究,例如内吹式襟翼的增升机理、几何参数影响、非定常吹气效应、气弹特性、升力响应特性、参数化方法及优化设计等。
内吹式襟翼失速迎角在较高的吹气动量系数下明显下降,限制了内吹式襟翼的应用潜力,可考虑使用前缘下垂设计来延缓失速,此外前缘下垂装置无缝隙,具有气动噪声小的优势。针对前缘下垂也有许多研究,例如通过前缘变弯度扩大层流 区从而 减小阻力;M.L.Preey等对低 雷诺数下FX63-137翼型的前缘下垂进行研究,结果表明,前缘下垂可使最大升力系数增加9.2%,前缘下垂5°时性能最好,并且由于当地前缘有效迎角减小,因此失速迎角增加;Niu J等研究了可变前缘下垂装置对NACA0012翼型动态失速控制的影响,结果表明,可变前缘下垂装置可抑制前缘涡,改善流动分离和动态失速特性。目前柔性材料的使用及前缘的结构设计能够实现翼型表面蒙皮光滑、无缝隙、大弯度变形,为其工程化应用提供了可能。
国内对前缘下垂及内吹式襟翼的组合设计研究、内吹式襟翼的失速机理和失速控制分析较少。国外,M.Burnazzi等研究了内吹式襟翼结合前缘下垂设计的气动特性,分析了不同前缘设计方法对内吹式襟翼失速特性影响,但对不同前缘下垂装置的失速特性和流场特征分析不够全面和细致,并且没有分析不同襟翼偏角下前缘下垂装置的作用效果。
本文针对前缘无缝下垂襟翼和后缘内吹式襟翼组合高升力设计,进行不同参数影响规律的工程应用研究;分析不同前缘设计对内吹式襟翼失速特性的改善效果,对流场特征进行规律总结;探究不同襟翼偏角下前缘下垂的作用效果。
1 内吹式襟翼模型设计
本文计算模型采用某亚声速无人机kink站位翼型,将翼型单位化(=1 m),翼型最大相对厚度为12%。襟翼弦长为0.25,初始襟翼偏角为65°,襟翼偏转轴为翼型下表面75%弦长处,射流缝高度=0.001。为了更精确地模拟射流,引入射流腔室,射流出口位于襟翼前缘,其与偏转轴的连线与弦线垂直,射流方向与出口处曲线相切。内吹式襟翼几何模型如图1所示。

图1 内吹式襟翼几何模型Fig.1 Internally blown flap geometry
2 数值求解方法
2.1 求解器计算精度验证
使用RANS方程求解器进行定常求解,全湍计算的湍流模型为-SST(Shear-Stress-Transport),本文采用基于有限体积法的中心离散格式,空间离散为二阶迎风格式,时间推进方式采用LU-SGS(Lower-Upper Symmetric Gauss-Seidel)隐式时间推进算法。
翼型在大迎角失速时,涉及到分离非定常效应,定常求解时升力波动,采用平均升力系数表示计算结果。30P30N翼型是道格拉斯公司设计的三段翼,已有大量计算和实验研究,是广泛应用于CFD验证的标模之一。本文使用30P30N三段翼用于CFD求解器精度验证。计算状态为=0.2,=5.0×10,计算网格如图2所示,采用结构网格,O型网格拓扑,计算域为75倍弦长,弦向前缘缝翼布置65个网格点,主翼布置203个网格点,襟翼布置105个网格点,网格量约32万,物面第一层网格高度为2×10,满足≤1。
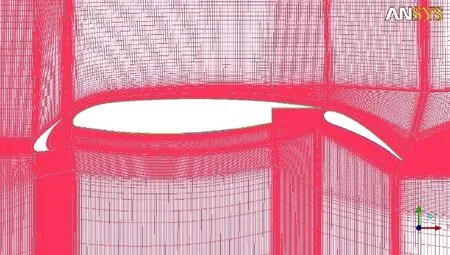
图2 30P30N翼型网格剖面Fig.2 Schematic of 30P30N airfoil mesh grid
升力系数计算值与实验值对比如图3所示,可以看出:30P30N翼型的计算结果在线性段与实验数据吻合较好,失速评估相较于实验值略微提前。因此采用的求解器满足工程应用研究需求的计算精度和可靠性。
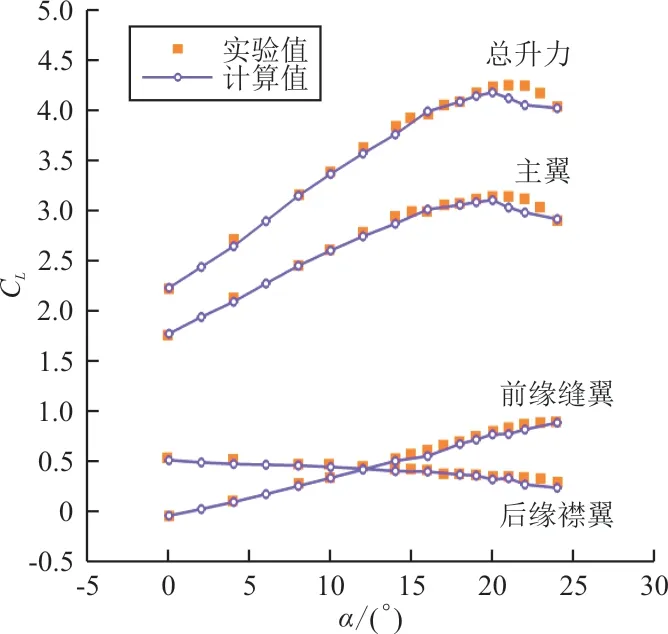
图3 30P30N翼型升力系数计算值与实验值对比Fig.3 Comparison of calculated and experimental results of the lift coefficient of the 30P30N airfoil
2.2 内吹式襟翼网格无关性
采用结构网格和C型网格拓扑对内吹式襟翼进行网格划分,如图4所示。在翼型前缘、射流出口襟翼上表面及后缘进行网格加密以精确捕捉流场结构和流动细节。

图4 内吹式襟翼网格划分Fig.4 Internally blown flap mesh grid
生成L0(46万)、L1(25万)、L2(6万)三套网格,计算结果如表1所示。在相同迎角下,使用6万的网格计算时相较于25万网格量,升力系数减小0.284 2,使用46万网格量相较于25万网格量,升力系数只增加了0.019 1,可认为46万与25万网格具有相当的计算精度,故采用25万网格量进行计算。
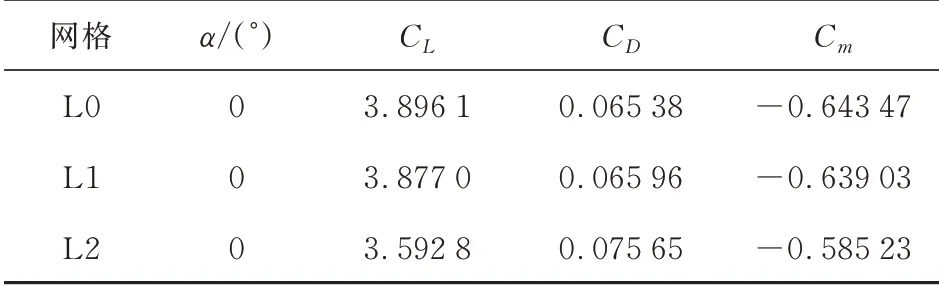
表1 网格无关性研究Table 1 Study on computational grid
3 内吹式襟翼的失速特性
采用吹气动量系数C衡量射流动量大小,通过给定射流腔室入口处的总温、总压从而改变吹气动量系数。
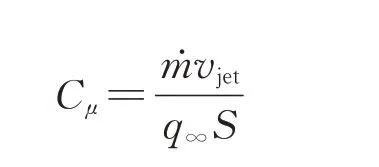
式中:̇为射流出口的质量流量;为出口射流速度;为自由来流动压;为参考面积。
计算状态为自由来流50 m/s,0°迎角下翼型升力系数随吹气动量系数变化曲线如图5所示。随着吹气动量系数增加,根据升力系数变化趋势,可分为附面层分离控制区和超环量控制区两个阶段,附面层分离控制区相较于超环量控制区,趋势线的斜率大,增升效率更高。定义临界吹气动量系数用于区分附面层分离控制区和超环量控制区。本文所采用内吹式襟翼临界动量系数C为0.024 3,对应的升力系数为3.53,与不吹气情况相比,升力增加85%。

图5 升力系数随吹气动量系数的变化曲线Fig.5 Variation of lift coefficient with jet momentum coefficient
不同吹气动量系数下升力系数随迎角变化曲线如图6所示,可以看出:最大升力的迎角在较高的吹气速度下明显下降,吹气动量系数为0时,失速迎角为12°,吹气动量系数为0.024 3时,失速迎角已下降为0°;当吹气动量系数再次增加时,失速迎角变化不大,吹气动量系数为0.081 2,失速迎角有略微增加。
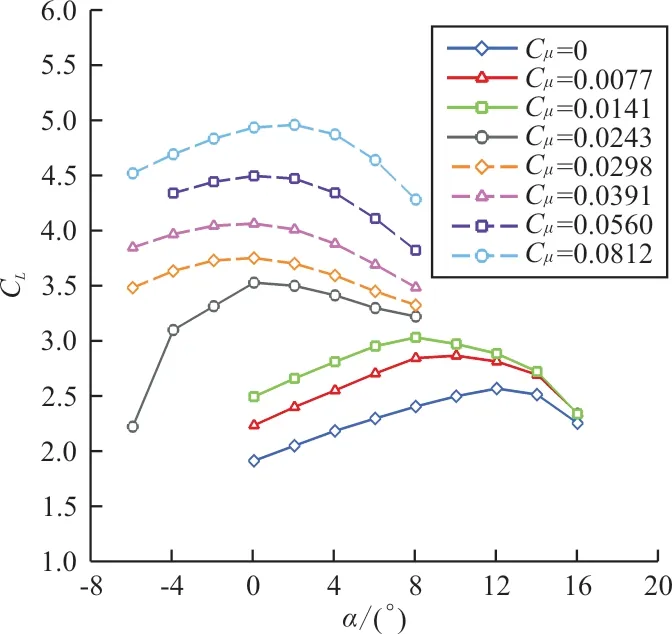
图6 不同吹气动量系数下升力系数随迎角变化曲线Fig.6 lift coefficient in function of angle of attack for different jet momentum coefficient
不同计算状态下翼型表面压力系数如图7所示,可以看出:射流动量增加,襟翼前缘负压峰值增大,内外压差增大使柯恩达效应增强,射流使翼型上表面气流流动加速的作用增强,前缘驻点后移,主翼前缘负压峰值增大,翼型有效迎角增加,失速迎角提前;增大迎角,主翼前缘负压峰值增加,逆压梯度增大,附面层动量损失厚度增加,襟翼前缘负压峰值减小。

图7 不同计算状态压力系数对比Fig.7 Comparison of pressure coefficient distributions for different calculation condition
柯恩达射流与外流相互作用下流线图如图8所 示,可以看出:C=0.014 1、=0°时的流 场 形态,射流动量较小,迎角小因而外流的边界层较薄,使得射流与外流混合后,在襟翼上表面产生分离;随着迎角的增大,前缘吸力峰值增加,附面层动量损失厚度增加,射流与外流之间的附着效应减弱,使得射流和外流之间产生分离,射流附着在襟翼表面(如图8(b)所示);吹气动量系数C=0.056 0,=0°时,属于超环量控制区,射流动量足以完全消除气流与襟翼分离(如图8(c)所示);迎角=8°时,翼型上表面逆压梯度增加,附面层动量损失厚度增加,射流和外流之间仍发生分离(如图8(d)所示)。
射流出口S1、S2位置示意图如图8(a)~图8(d)所示。
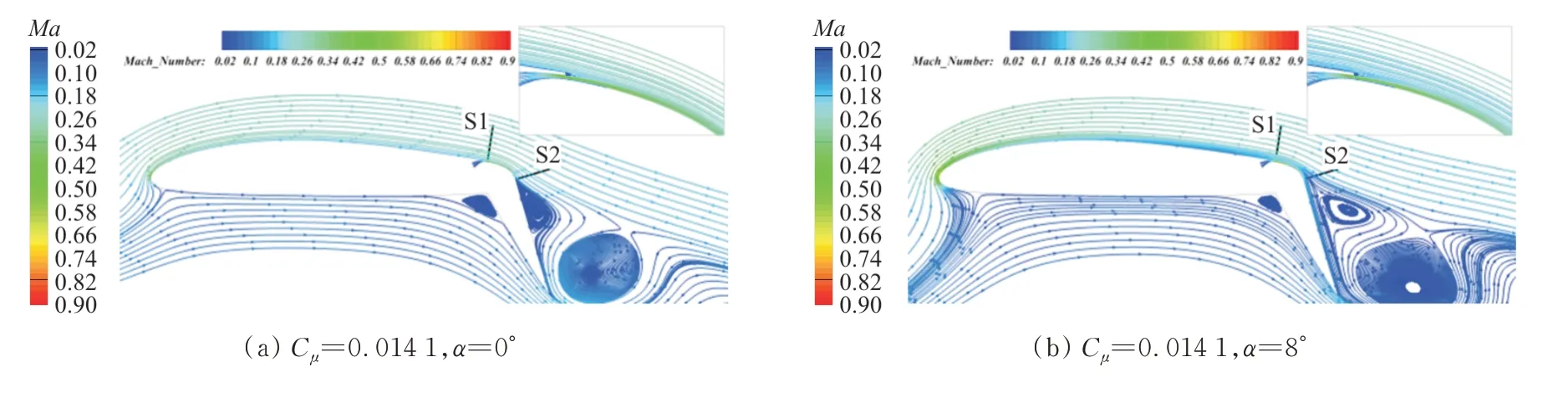

图8 不同吹气动量系数柯恩达射流与外流相互作用下流线图Fig.8 Ma contour and streamlines of the interaction between Coanda jet and outflow for different jet momentum coefficient
S1位于射流出口处,吹气动量系数越大,射流速度越大;吹气动量系数不变,增加迎角,前缘的黏性损失和逆压梯度增加,降低了到达射流出口时的外流动量,射流出口处静压增大,射流出口速度减小。从S2位置分析射流与外流的混合,C=0.056 0相较于C=0.014 1,吹气动量系数增加,有更多的射流能量传递到外流,射流使边界层下部区域流动加速,上部区域气流仍有较大的动量损失,随着迎角增加,气流的动量损失增加。当C=0.081 2时(如图8(e)和图8(f)所示),射流增强了向外流的动量传递,外流能克服较强的逆压梯度,故失速略微延迟。
不同吹气动量系数下速度型对比如图9所示。
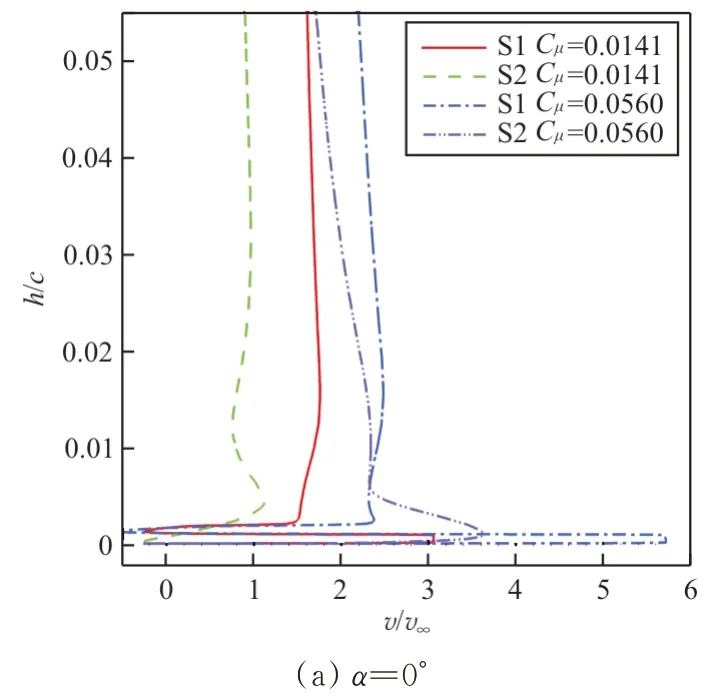
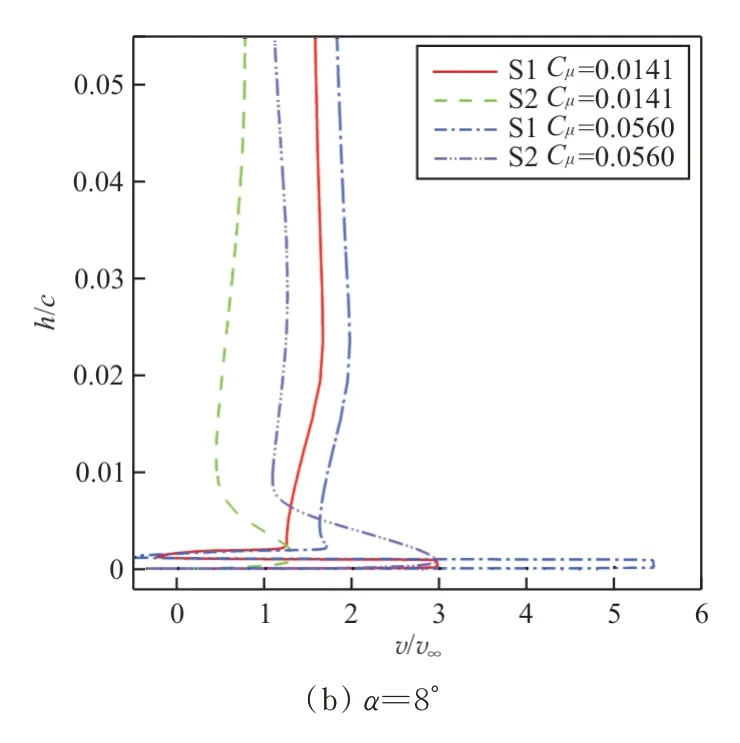
图9 不同位置速度型对比Fig.9 Comparison of different position velocity profiles
4 前缘下垂设计
本文采用刚性偏转、增加弯度和厚度等方法对前20%翼型弦长的几何外形进行修改,实现前缘下垂设计。设计的几何约束包括保持前缘下垂段的表面弧长不变,以便在结构上可以使用非拉伸的柔性蒙皮。
4.1 前缘刚性偏转失速特性分析
前缘刚性偏转技术成熟度高,在不改变前缘形状的条件下,将前20%翼型型面绕给定转轴进行偏转,本文所给转轴位置、初始翼型和前缘偏转5°、10°、20°、30°、35°、40°的几何外形对比如图10所示,定义前缘刚性偏转角为。

图10 不同前缘刚性偏转构型Fig.10 Different rigid droop-nose configurations
C=0.056时前缘不同刚性偏转角下升力系数随迎角的变化曲线如图11所示,可以看出:刚性偏转30°效果最好,最大升力系数为4.76,失速迎角为4°,与前缘无偏转构型相比,最大升力系数增加0.267,失速迎角推迟4°。
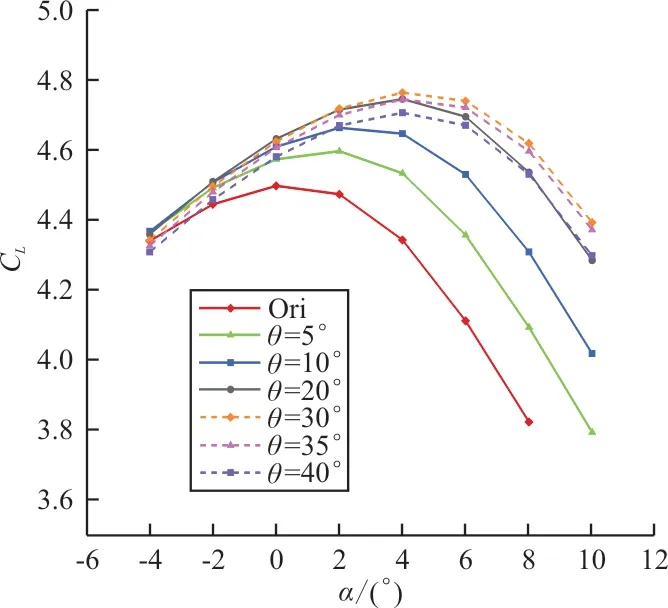
图11 不同前缘刚性偏转构型失速性能对比(Cμ=0.056)Fig.11 Comparison of stall characteristics for different rigid droop-nose configurations(Cμ=0.056)
=4°时,不同前缘刚性偏转构型压力系数、前缘驻点位置和前缘边界层动量厚度对比如图12所示。前缘部分有两个明显的负压峰(如图12(a)可所示),分别定义为前缘处的负压峰和连接处的负压峰,前缘刚性偏转,上表面连接处的曲率增大,气流产生二次加速,因此产生负压峰;随着前缘偏角的增大,翼型前缘负压峰值减小,连接处的负压峰值增加,前缘偏角从0°增加到30°时,连接处第二个吸力峰的形成使得逆压梯度降低,延缓上翼面流动分离,因此推迟了失速迎角,增加了最大升力系数;但继续增加前缘偏角时,连接处的负压峰值过大,前后缘压差又逐渐增加,边界层的黏性损失增加,因此升力系数减小。
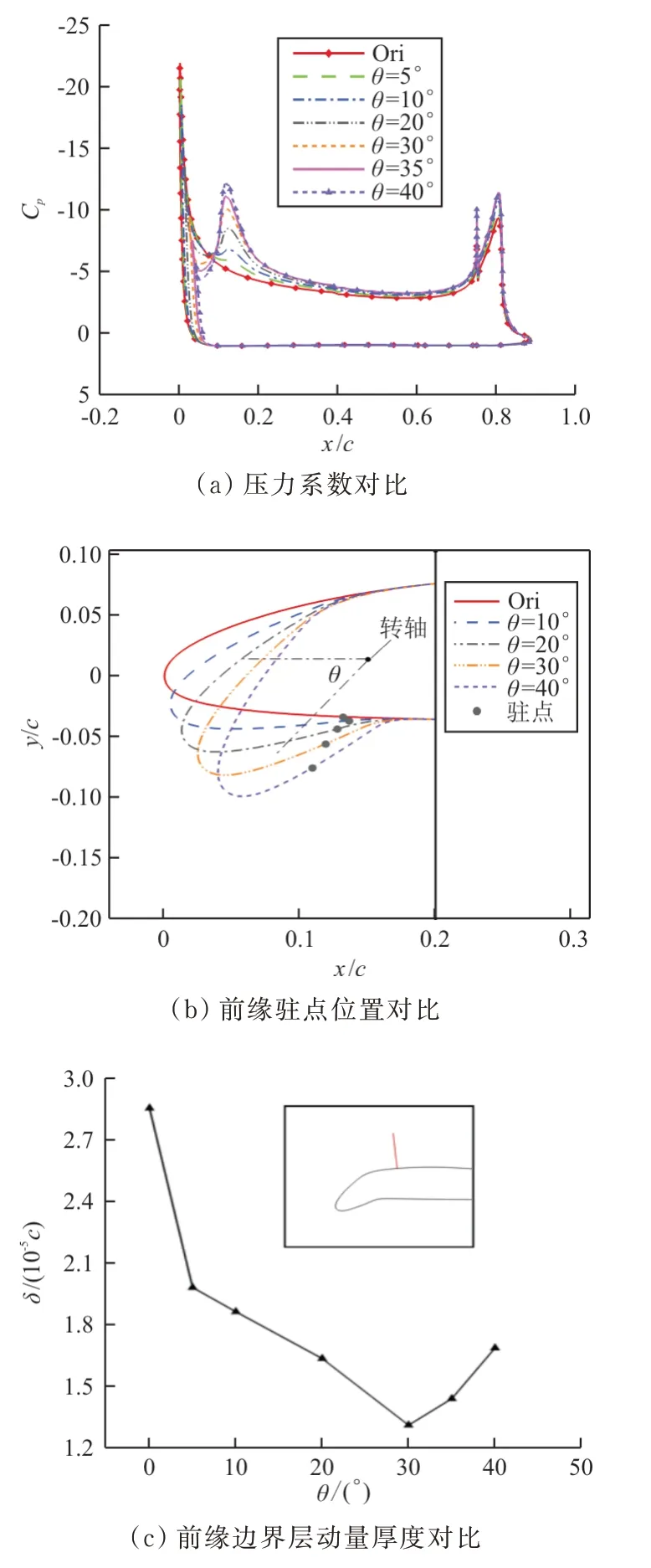
图12 不同前缘刚性偏转构型压力系数、前缘驻点位置和前缘边界层动量厚度对比(α=4°)Fig.12 Comparison of pressure coefficient distributions,leading edge stagnation point position and boundary layer momentum thickness for different rigid droop-nose configurations(α=4°)
从图12(a)可以看出:前缘偏角增加造成前缘吸力损失,前缘载荷减小,使得抬头力矩减小,低头力矩增大,不利于飞机起降阶段的俯仰力矩配平。
从图12(b)可以看出:随着前缘偏角的增大,前缘驻点前移,说明前缘局部有效迎角逐渐减小。
从图12(c)可以看出:边界层动量厚度在前缘偏转30°时黏性损失最小,说明了此时内吹式襟翼失速特性的改善效果最好。
为了更直观地了解前缘不同刚性偏转构型前缘流动特征,=4°时不同前缘刚性偏转构型马赫数云图对比如图13所示,可以看出:初始翼型前缘位置出现马赫数峰值且为单峰值,随着前缘偏角的增大,以0.34等值线为例,可以看到较高马赫数区域的面积逐渐增大,马赫数峰值由单峰值转变为双峰值;=40°时,马赫数峰值由前缘后移至连接处位置,且又变为单峰值。
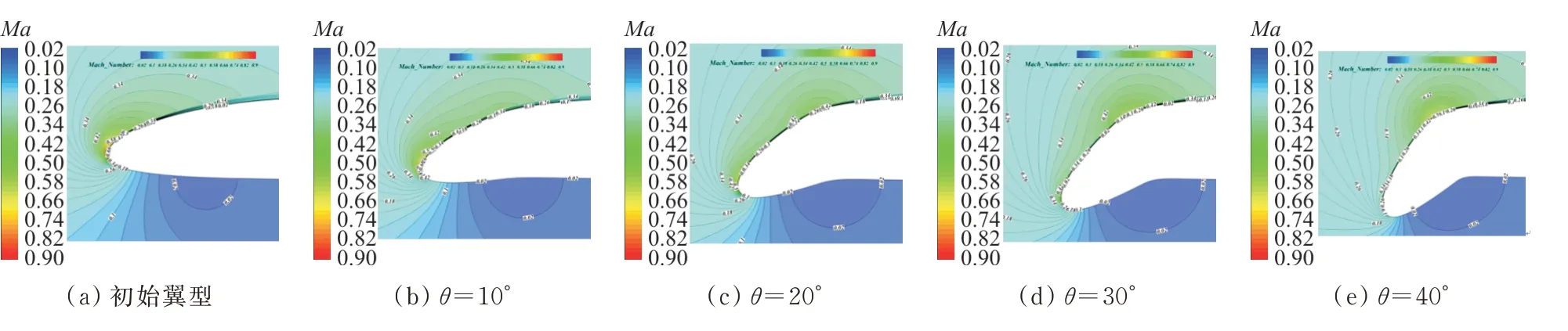
图13 不同前缘刚性偏转构型马赫数云图对比(α=4°)Fig.13 Comparison of Ma contour for different rigid droop-nose configurations(α=4°)
综上所述,前缘或连接处的负压峰值过高,为单峰值时,导致翼型性能恶化,通过适当的前缘偏转,将过高的单峰值转变为较低的双峰值能有效提高失速特性。
=30°时不同迎角下的翼型表面压力分布如图14所示。流动发生分离是黏性和逆压梯度共同作用的结果,随着迎角增加,环量增加,前缘处和连接处的负压峰值增加,在逆压梯度的作用下,促使边界层厚度迅速增加,导致=4°时开始失速。

图14 θ=30°构型不同迎角下压力系数对比Fig.14 Comparison of pressure coefficient distributions of θ=30°configurations for different angle of attack
在同一襟翼偏角下,迎角越大,前缘流动加速明显,因此前缘负压峰值越大。但迎角增大,在射流缝上游的黏性损失增大,边界层动量厚度增加,使射流缝处外流能量较低,静压增大,射流腔室与外流压差减小,射流速度减小,对外流的加速作用减弱,因此襟翼处负压峰值减小。
4.2 前缘弯度增加失速特性分析
前缘变弯度偏转通过逐渐改变翼型前缘表面曲率实现偏转,翼型弦长前20%用新的弧线代替,为了简化,弧线的曲率半径恒定,不同曲率半径得到的弧线控制前缘变弯程度,翼型厚度分布保持不变,定义弧线对应的圆心角参数为。
为15°,30°,45°,60°,75°,90°时的几何外形如图15所示。在不同取值下,曲率半径的确定需满足前缘下垂段变弯前后长度相等的要求。
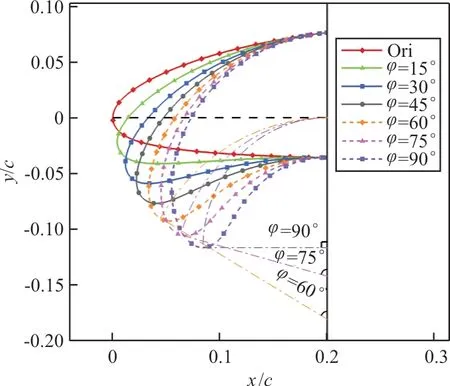
图15 不同前缘变弯度偏转构型Fig.15 Different lead edge camber increase configurations
C=0.056时不同前缘变弯度构型的性能对比如图16所示。
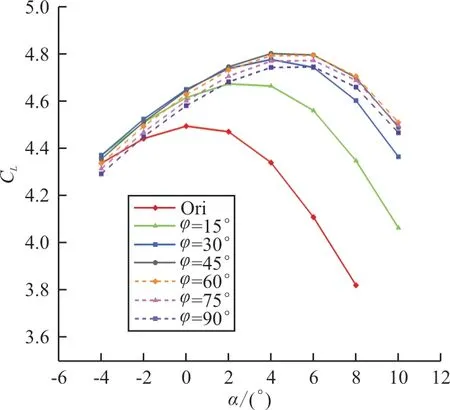
图16 不同前缘变弯度构型的性能对比(Cμ=0.056)Fig.16 Stall characteristics of different lead edge camber increase configurations(Cμ=0.056)
从图16可以看出:变弯度最佳构型为=45°,最大升力系数为4.8,失速迎角为4°,与前缘无变弯构型相比,最大升力系数增加0.3,失速迎角推迟4°。
=4°时不同前缘变弯度下翼型表面压力系数如图17(a)所示,可以看出:随着变弯程度的增加,前缘负压峰值减小,前缘气流缓慢加速,逆压梯度减小,有效提高了失速迎角,增加了升力系数,前缘变弯度构型相较于刚性偏转构型,连接处曲率变化量小,没有明显的前缘二次负压峰的现象,低压在前缘较大的范围内分布;变弯程度过大时(45°时),前缘弦长减小使前缘升力略有损失,前缘低压范围后移,前缘负压峰进一步减小,升力系数增加量相较于前缘低变弯程度构型有所减小,最大升力系数减小。
=4°时不同前缘变弯度构型前缘驻点位置如图17(b)所示,可以看出:随着变弯程度的增加,前缘驻点前移,减小了前缘局部有效迎角。
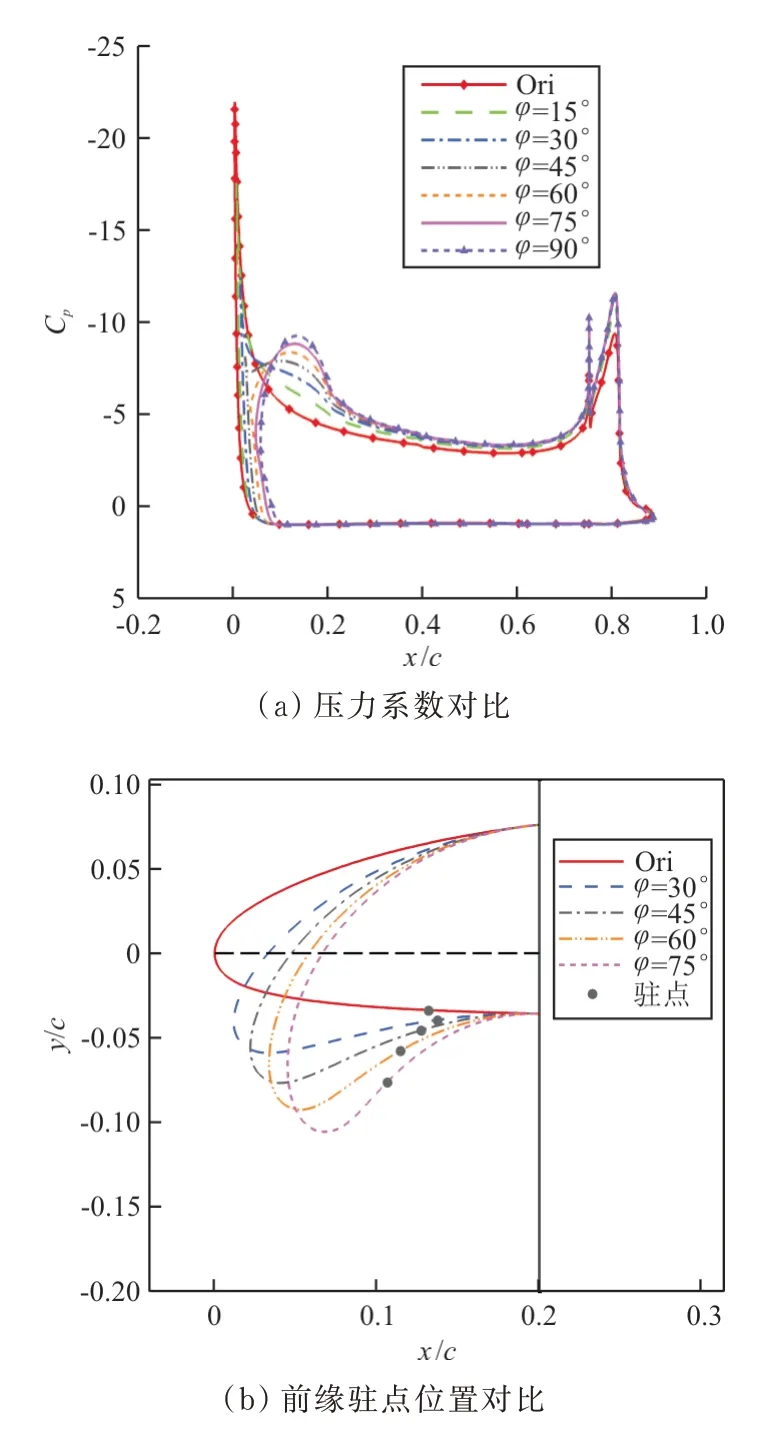
图17 前缘变弯度构型压力系数和前缘驻点位置对比(α=4°)Fig.17 Comparison of pressure coefficient distributions and leading edge stagnation point position for different lead edge camber increase configurations(α=4°)
=4°时不同前缘变弯度构型马赫数云图如图18所示。相较于初始翼型,前缘弯度增加构型马赫数峰值减小,气流加速变缓且加速范围增加,以0.34等值线为例,较高马赫数区域的面积增大并后移。

图18 不同前缘变弯度构型马赫数云图对比(α=4°)Fig.18 Comparison of Ma contour for different lead edge camber increase configurations(α=4°)
4.3 前缘厚度增加失速特性分析
增加翼型的前缘半径有助于改善低速性能,提高翼型的升力系数,可以通过增加前缘厚度来增大前缘半径。定义二次函数,满足(0.2)=1,′(0.2)=0,(0)=,通过值控制前缘厚度,然后将翼型上各点到中弧线的距离乘以函数来改变前缘厚度,前缘加厚构型计算结果如图19所示。本文结合厚度和弯度变化,在前缘变弯度45°和60°的基础上增加前缘厚度,模型如图19(a)和图19(b)所示。
C随变化的计算结果如图19(c)和图19(d)所示,可以看出:改善效果不明显,=45°构型最大升力系数和失速迎角恶化;=60°,=1.4构型大迎角的升力系数有略微提升。
=45°构型=6°时压力系数对比如图19(e)所示,由于前缘厚度增加,前缘20%处左侧曲率减小,故加厚构型前缘二次负压峰的现象进一步削弱。=45°构型前缘弯度增加,低压在前缘较大的范围内上分布,前缘顺压梯度的范围增加,流动加速的范围增加,在变弯度的基础上增加前缘厚度,前缘半径增大,但前缘上表面约2%~10%范围内的曲率相较于不加厚构型曲率增加,加厚构型的上表面曲率的增加使得流动进一步加速,因此加厚构型的负压峰值增加,相应的逆压梯度增大,边界层的厚度增加,对最大升力系数和失速迎角改善效果不明显。
=60°构型=6°时压力系数对比如图19(f)所示,可以看出:=60°构型相较于=45°构型前缘低压范围后移,增加厚度后,前缘上表面约2%~10%范围内的曲率减小,故促进流动加速,使负压峰值前移且略微增加。随着厚度进一步增加及迎角的增大,引起的逆压梯度的增加使边界层厚度增加,无法改善失速迎角,也造成升力系数的损失,其最优厚度控制参数为1.4。

图19 前缘加厚构型计算结果(Cμ=0.056)Fig.19 Result of lead edge thick increase configurations(Cμ=0.056)
4.4 结果对比分析
初始翼型、=30°构型和=45°构型在给定迎角下射流缝上游翼型表面的速度型对比如图20所示,可以看出:初始翼型0°迎角下的速度型和前缘刚性偏转30°构型、前缘变弯度45°构型4°迎角下的速度型相似,尤其在C=0.056时吻合程度较好,说明前缘下垂装置有效延缓了翼型边界层动量厚度随迎角增加而增加的趋势。
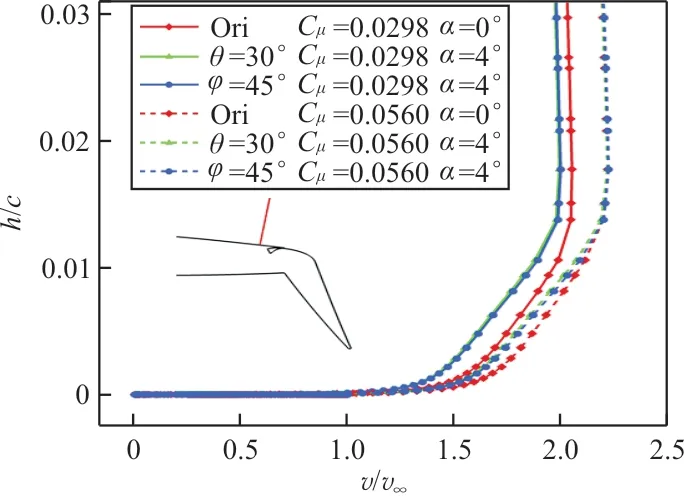
图20 射流翼缝上游的速度型对比Fig.20 velocity profiles comparison over the jet slot
射流缝上游边界层动量厚度对比如图21所示,射流动量系数的增加增强了对翼型上表面气流的卷吸作用,减小了翼型边界层动量厚度。所有构型随着迎角的增加在射流缝上游的黏性损失增大,边界层动量厚度增加,采用前缘下垂装置有效减小了射流缝上游边界层动量厚度,且前缘变弯度45°构型相较于刚性偏转30°构型效果更好。
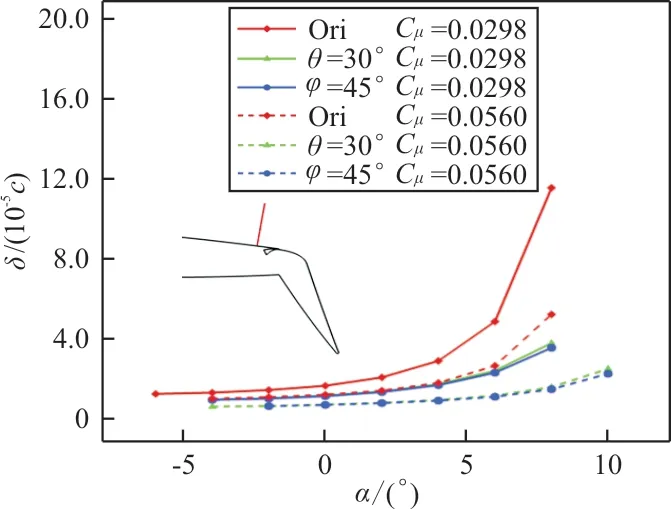
图21 射流翼缝上游边界层动量厚度对比Fig.21 layer momentum thickness comparison
初始翼型、=30°和=45°构型在C=0.056,=4°时前缘驻点流线如图22所示,可以看出:=30°和=45°构型前缘驻点位置相较于初始翼型均前移,=30°构型因前缘偏转程度更明显,前缘驻点位置更靠前,但=45°构型前缘曲率变化率小,更有助于失速特性的改善。

图22 前缘驻点流线对比(Cμ=0.056,α=4°)Fig.22 leading edge stagnation point streamlines comparison(Cμ=0.056,α=4°)
5 襟翼偏角对失速特性的影响
襟翼偏角55°,C=0.056时前缘不同变弯度构型的气动性能对比如图23所示,可以看出:=60°时,最大升力系数为4.60,失速迎角为8°,与前缘无偏转构型相比最大升力系数增加0.38,失速迎角增加4°。

图23 不同前缘变弯度构型的性能对比(Cμ=0.056)Fig.23 Stall characteristics of different lead edge camber increase configurations(Cμ=0.056)
襟翼偏转65°时=0°和=45°构型、襟翼偏转55°时=0°和=60°构型最大升力系数和失速迎角随C增大的变化情况对比如图24所示。
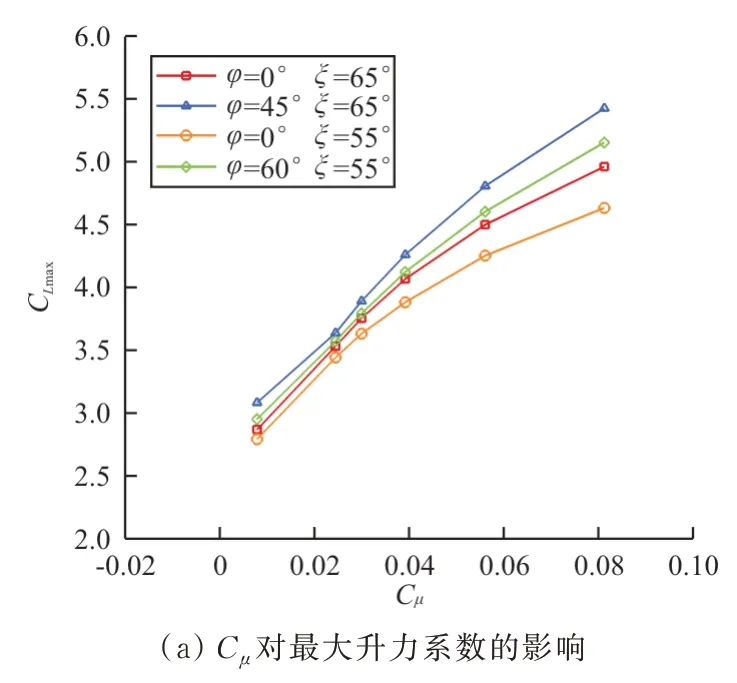
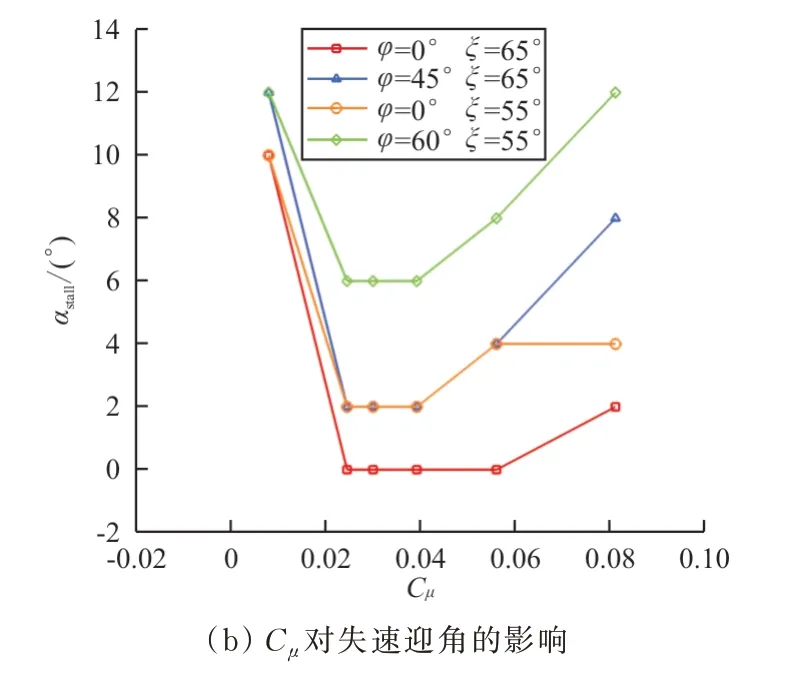
图24 Cμ对不同构型失速特性的影响Fig.24 Effect of Cμ on stall characteristics for different configurations
从图24可以看出:随着吹气动量系数的增加,翼型最大升力系数增加,但是失速迎角先下降后略有增加。吹气动量系数较小时,翼型在小迎角时就可能发生失速,失速后,机翼上的分离流会对飞机的飞行品质、操稳、结构等造成严重的危害,增加升力并延迟失速迎角是低速飞行安全的重要保证。在超环量控制区,随着吹气动量系数增加,升力增加,失速迎角增加,有利于飞机起飞着陆阶段的失速控制和飞机的低速飞行安全。
襟翼偏角增加会增大升力系数,减小失速迎角,相同吹气动量系数C=0.081 2下,前缘变弯设计使襟翼偏转65°构型失速迎角增加6°,襟翼偏转55°构型失速迎角增加8°。后缘襟翼偏角从65°减小到55°,失速迎角从8°增加到12°,最大升力系数从5.42降低到5.15,因此襟翼偏角设计时需要根据设计升力系数和失速迎角的需求合理选择。
C=0.081 2时,襟翼偏角65°、45°构型和襟翼偏角55°、60°构型在=8°时表面压力分布和流线对比如图25所示。
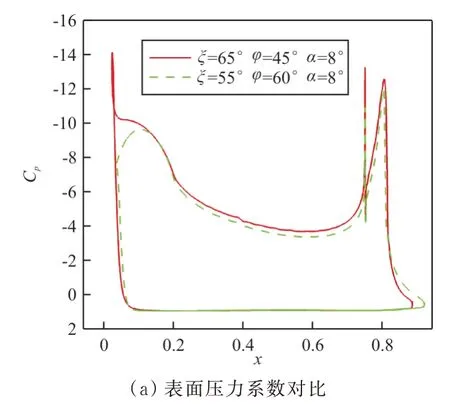
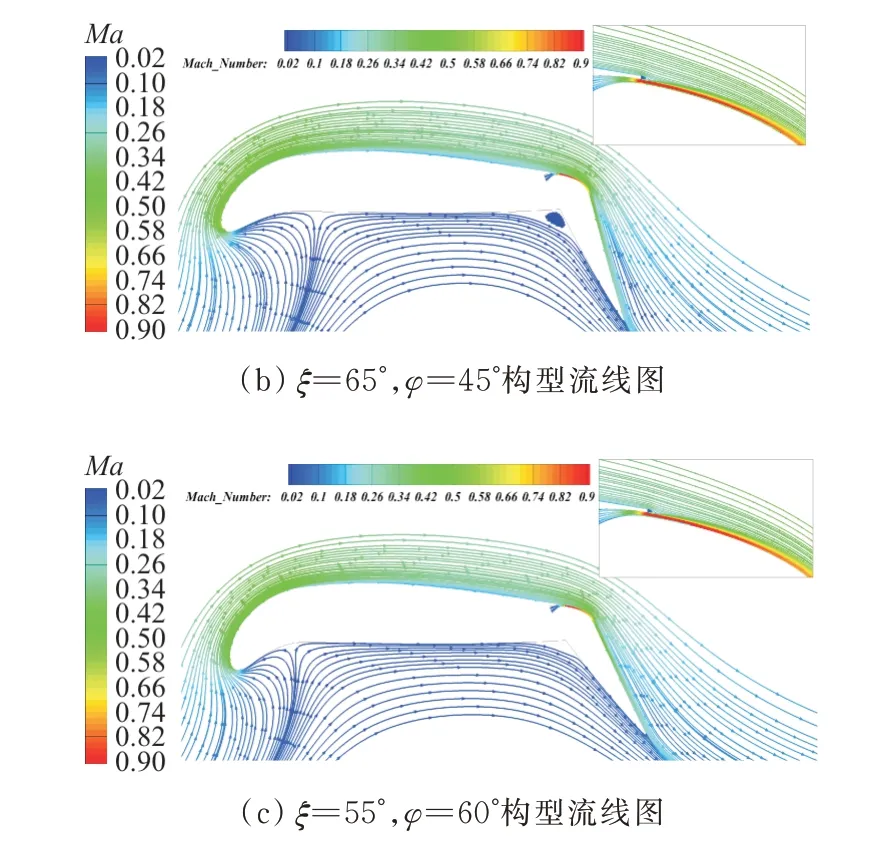
图25 表面压力系数及流线对比(Cμ=0.081 2,α=8°)Fig.25 Pressure coefficient distributions and streamlines comparison(Cμ=0.081 2,α=8°)
施加吹气时,增加襟翼偏角,襟翼吸力峰值增大,襟翼部分的升力增大,对主翼产生的上洗作用增强,因此翼型前缘的吸力峰值也增大,主翼上表面的压力系数减小,升力系数增加,但襟翼上表面逆压梯度增大,对流动的阻碍作用增强,射流能量对外流的加速作用减弱,尾流中低速区域增大,易发生流动分离,因此失速迎角提前。
6 结论
(1)随着吹气动量系数C的增加,内吹式襟翼最大升力系数增加,在附面层分离控制区,失速迎角随C的增加迅速下降,而在超环量控制区,由于射流动量系数的增加,增加了翼型上表面气流的能量,减小了翼型边界层动量厚度,失速迎角增加。
(2)通过前缘下垂设计,改善了翼型前缘附近的压力分布,靠近前缘的局部迎角减小,从而减小了不利的压力梯度及当地马赫数,延缓了翼型边界层动量厚度随迎角增加而增加的趋势,延迟了流动分离,有效提高了失速迎角,增加了大迎角下的升力系数,使得在获得相同升力系数时吹气动量减小。
(3)前缘刚性偏转技术成熟度高,但连接处曲率增加,导致产生第二个负压峰值,在C较大时,限制了其作用效果。前缘变弯度设计可采用柔性蒙皮,通过逐渐改变前缘表面曲率实现,对最大升力系数和失速迎角的改善作用更好。在前缘变弯度构型的基础上增加前缘厚度,对失速特性的改善作用并不明显。
(4)前缘下垂结合内吹式襟翼设计能在提高翼型最大升力系数的同时改善失速迎角,是一种有效的动力增升装置的失速改善方案。
