基于KPCA-BLSTM的航空发动机多信息融合剩余寿命预测
2022-06-24胡启国白熊杜春超
胡启国,白熊,杜春超
(重庆交通大学机电与车辆工程学院,重庆 400074)
0 引言
航空发动机在正常运行中发生事故,会造成巨大的经济与社会损失,为了保证航空发动机可靠、安全地运行,利用设备监测数据对其进行剩余寿命预测显得尤为重要,可以为设备提前检修提供参考依据。
众多研究者对剩余寿命预测进行了深入研究。裴洪等总结和分析了基于机器学习的设备剩余寿命(Remaining Useful Life,简称RUL)预测方法,通过分析基于机器学习的剩余寿命模型理论和模型内部结构的层数,将其分为浅层机器学习和深度学习的方法;武博等提出利用主成分分析建立不同程度判断标尺构建导弹筒寿命预测模型,实现对导弹筒的全周期寿命评估;杜方舟等基于航空发动机排气温度裕度数据,利用遗传算法优化基于支持向量机的剩余寿命预测模型,最终拟合出的寿命曲线与原厂数据高度切合,得到较好的预测效果;高峰等通过多域特征量对数据集进行扩充,并搭建了长短时记忆(Long Shortterm Memory,简称LSTM)神经网络寿命预测模型,最终利用C-MAPSS数据集验证了该方法的可靠性;马忠等通过改进卷积神经网络(Convolutional Neural Networks,简称CNN)解决了航空发动机多状态变量下的非线性特征导致剩余寿命预测困难的问题,结果表明改进CNN进行寿命预测的准确性得到显著提高;牟含笑等提出基于深度置信网络与BLSTM神经网络的航空推进系统剩余寿命预测方法,该方法适用于时间序列的处理;李杰等等提出一种融合神经网络的剩余寿命预测方法,该方法精度高且具有良好的鲁棒性;车畅畅等将一维卷积神经网络与BLSTM神经网络混合模型运用到航空发动机的剩余寿命预测中,准确地预测寿命变化的结果,相较于单一使用BLSTM或CNN网络模型的预测精度有所提高;曾慧洁等通过模型对样本集正反序列的训练学习,建立了BLSTM网络模型来预测航空发动机故障,并将结果与其他神经网络模型对比,表明双向长短时记忆神经网络预测精度更高;宋亚等提出了一种基于自动编码器和双向LSTM的混合模型来预测涡轮发动机的RUL,并获得了比LSTM模型更好的预测结果。针对航空发动机寿命预测问题,国外E.L.Ntantis等总结了航空发动机故障与提前维修预测方法,对比了物理建模、人工神经网络、贝叶斯神经网络、CNN等多种方法,得出基于神经网络的预测方法更加快速、准确;I.Remadna等考虑航空发动机退化数据特征提取困难的问题,利用CNN对复杂退化信息进行提取,再利用BLSTM神经网络对航空发动机剩余寿命进行了预测,通过C-MAPSS数据集验证了该方法;C.Ordóñez等提出一种由差分自回归移动模型与支持向量机组成的混合模型对航空发动机RUL进行预测,通过航空发动机数据集验证了该模型,并取得不错的预测效果。
虽然众多研究者所提出的RUL模型都取得了不错的预测效果,但大多研究者在预测时并未考虑数据间的非线性关系及多信息冗余问题导致模型训练时学习过多产生不必要的信息而使得预测精度大打折扣的问题。
本文提出利用核主成分分析处理非线性数据的优越性,对多维退化性息进行融合降维;针对BLSTM神经网络处理时间序列的能力提出一种基于KPCA-BLSTM神经网络的航空发动机多信息融合剩余寿命预测模型,并利用C-MAPSS航空发动机数据集进行对比验证,并与SVR、CNN、BLSTM神经网络模型的预测结果进行对比。
1 双向长短时记忆神经网络原理
航空发动机的退化过程是一个累积的过程,状态变化不仅与当前时刻的监测信息有关,而且某个历史时刻的信息也会影响设备的状态变化。国内外研究者提出的LSTM神经网络,相对于普通循环神经网络(Recurrent Neural Networks,简称RNN),既可以更好地处理长时间序列的数据信息,又可以解决训练过程中的梯度消失和梯度爆炸问题。
1.1 LSTM神经网络

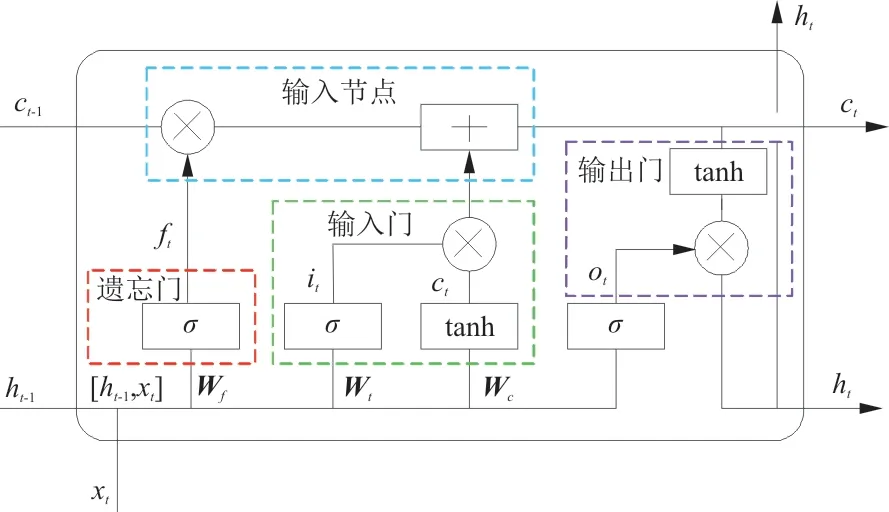
图1 LSTM神经单元示意图Fig.1 Schematic diagram of LSTM neural unit
LSTM模型通过使用由上一层输出的h和当前时间输入的x组成的输入向量计算遗忘门f来控制存储单元的状态:

式中:W为输入层的权重矩阵;b为偏置向量;(·)为激活函数,即sigmoid函数。
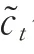
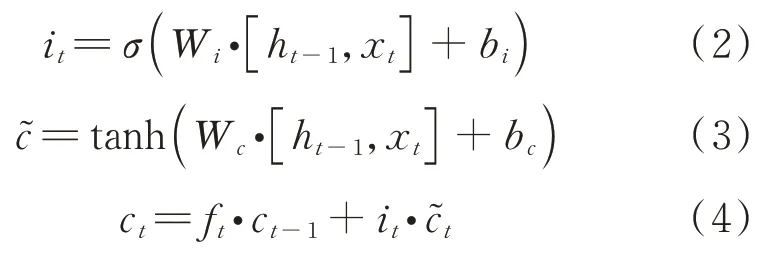
式中:W,b分别为状态更新层的权重和偏差。
信息传递到输出层后,网络通过输出门o控制更新状态的输出。
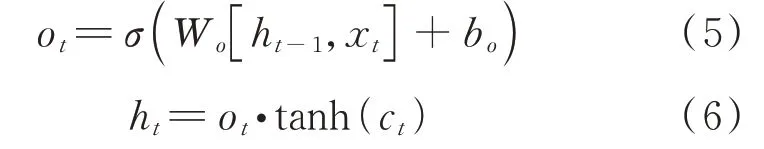
式中:W,b分别为输出层的权重和偏差。
1.2 双向LSTM神经网络
双向LSTM神经网络由LSTM层的两个方向组成。在长时间序列的训练过程中,可以从正反两个方向捕获整个序列的信息,具有比LSTM更高的性能。双向LSTM结构如图2所示。
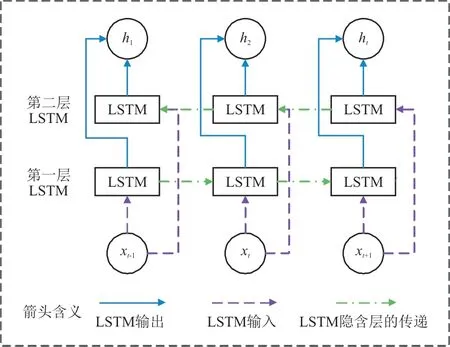
图2 双向LSTM结构示意图Fig.2 Schematic diagram of BLSTM structure
第一层LSTM结构计算当前输入的正向序列信息,第二层LSTM结构反向计算相同的序列,两层结构均存在相互独立的隐含层。LSTM结构层间的隐含层输出,不仅要传递给下一层的输入层,而且通过双向LSTM结构还需要传递给上一层的输入结构中。在训练过程中,通过对输出单元的正反向传播,完成对神经网络的权重更新。
2 多信息融合RUL预测模型
2.1 预测模型建立
航空发动机在投入到生产使用过程中受到内部因素和外界环境的影响,其性能会发生退化,各项性能指标也会相应降低,直至失效完全失去工作能力。在实际试验或运用中,会通过各种传感器获得这些设备的现场运行监测数据,这些数据可视为以设备运作为基础的时间序列。
设一组设备的监测数据可表示为
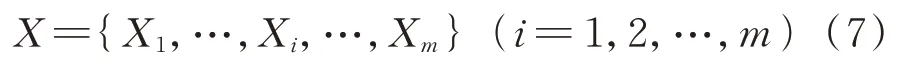
式中:X为第台设备的所有运行状态监测数据集合。
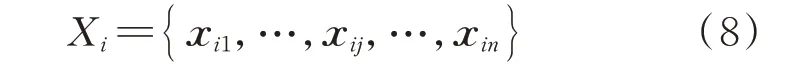
式中:x为第台设备的第个状态监测变量的时间序列。
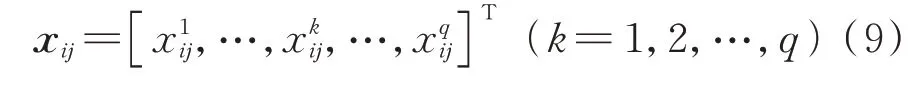
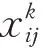
因此,与第台监测设备的状态数据相对应的剩余寿命集合表示为

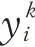
基于以上思想,本文提出一种针对多状态多维度退化特征的监测数据RUL预测模型,整体流程如图3所示。
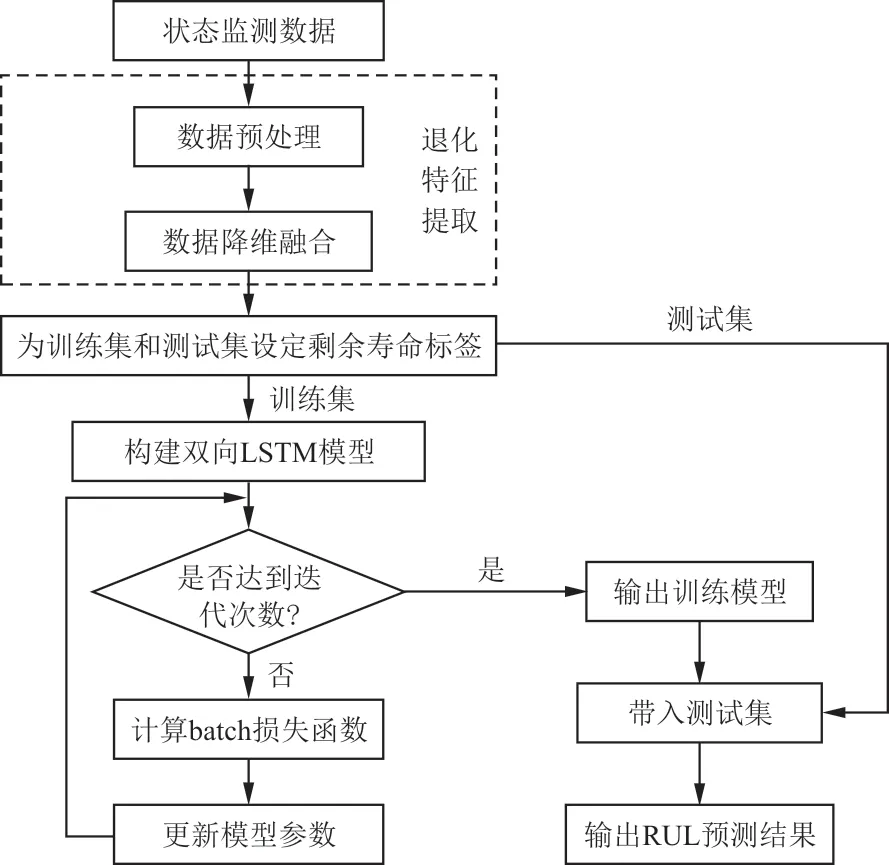
图3 RUL预测模型流程图Fig.3 RUL prediction model flowchart
由于整个模型的输入为多状态监测数据,首先进行数据预处理,并采用KPCA对预处理后的多维状态数据进行融合降维;其次添加RUL标签,按照时间窗大小对低维监测数据的时间序列进行划分,并建立双向LSTM深度学习网络模型;然后分别设置批量(batch)从20开始,以10个批量为间隔数增加,根据每个迭代次数的平均损失函数与更改模型权重参数选取最佳批量,直至损失减小并趋于稳定;最后将测试数据导入模型进行验证,通过评价模型判断模型训练的效果。
2.2 数据预处理
在进行预测之前,需要对多状态监测数据进行预处理,为了使设备的真实值和预测值在训练时表现出差异性,需要对数据集添加RUL标签。退化过程是退化量累积的过程,在航空发动机运行初期,退化特征并不明显,一段时间后设备能够平稳运作,直到运行到某一阶段,设备开始进入加速退化阶段,并出现故障,因此采用分段线性模型进行预测,如图4所示。
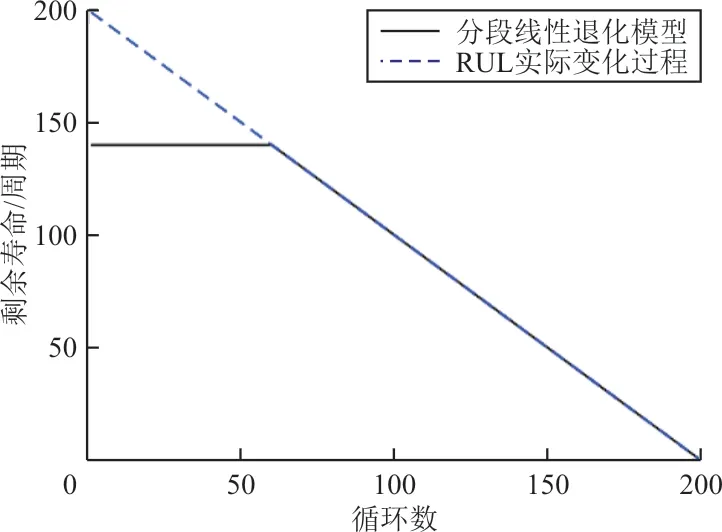
图4 分段线性模型Fig.4 Piecewise linear model
为了消除传感器参数范围的差异,对每组传感器监测的数据进行线性归一化处理,使得处理后的参数值在[0,1]的范围内。其表达式为

2.3 模型输入
经过数据预处理后,采用KPCA进行降维,然后根据方差贡献量选择适当的维数。在模型训练过程中,为了防止模型出现过拟合现象,在双向LSTM层与全连接层中添加一个Dropout层,并且设置一定的丢弃率去掉隐含层部分输出值,确保神经元在正向传播中不被影响。根据时间步长对训练集和测试集进行分割,并将分割后的训练集输入到双向LSTM模型中。选择均方误差作为损失函数,其表达式为
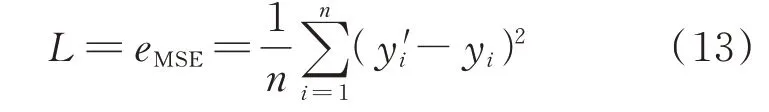
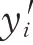
2.4 模型评价标准
利用同样处理训练集的方法对测试集进行数据处理,并输入到训练后的神经网络模型中,输出RUL预测值。为了定量评价模型预测能力,采用均方根误差和非对称评分函数作为评价依据。
均方根误差可以反映预测误差的大小,其表达式为

非对称评分函数能够通过判断预测值是否大于或小于真实值而给出截然不同的计算结果,其中评分正比于误差,其函数表达式为
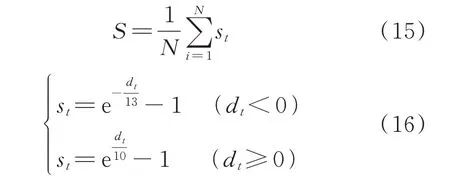
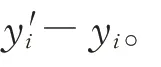
3 对比验证
3.1 数据集介绍
本文采用C-MAPSS数据集进行仿真验证,数据集由四个子集组成,包含6种不同的工作条件和4种故障形式,每个子集记录了在不同工作条件和故障类型下航空发动机的健康状况退化数据。CMAPSS数据集中包含的全部信息如表1所示。
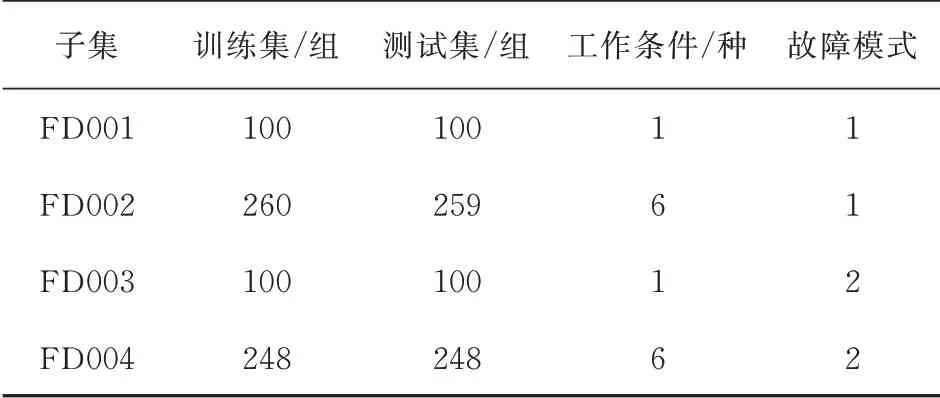
表1 航空发动机监测数据Table 1 Aero engine monitoring data
选用FD003子集作为实验数据集,FD003数据集包括3个工作条件参数:飞行高度,马赫数和油门旋转变压器角度,它们可以组合成六个对发动机性能有重大影响的工作条件。数据还包括21个发动机传感器,例如风扇入口处的压力,燃烧器的燃料空气比和旁路比。FD003的故障模式为HPC退化和风扇退化失效。
3.2 仿真验证
为了减小训练模型的复杂度,增强其稳定性,选用KPCA对发动机高维数据进行降维,KPCA是一种常用的数据融合和维数约简方法,即构造高维特征空间,把原始变量转化为空间内积矩阵,并利用原始变量空间的核函数代替内积函数。为了确定目标降维量,将累计方差贡献量作为目标降维量选取的标准,经计算得出各特征的方差贡献量如图5所示,前10维累计方差贡献量达到0.95,由此选定10维作为目标降维量。
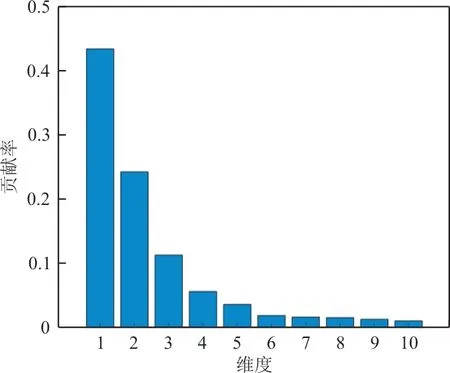
图5 KPCA方差贡献量Fig.5 KPCA variance contribution
经KPCA降维后,根据时间步长对训练集和测试集的时间序列进行划分。输入模型的3D张量为(24 720,50,10)。在将数据输入模型之前,需要设置模型的各种参数。模型参数直接影响模型的性能,选择合适的神经网络参数对模型的训练成功与否起着至关重要的作用,经反复调试参数后,确定模型的主要参数,如表2所示。

表2 BLSTM神经网络参数设置Table 2 BLSTM neural network parameter settings
将输入模型的数据集以9∶1的比例划分为训练集和验证集。设置“提前停止”的参数,如果在10个周期内验证集的误差无下降趋势,则将停止训练。利用验证集(即100组发动机)验证模型准确度,验证结果如图6所示,可以看出:预测值与真实值的拟合度较高,说明模型的预测效果较好。
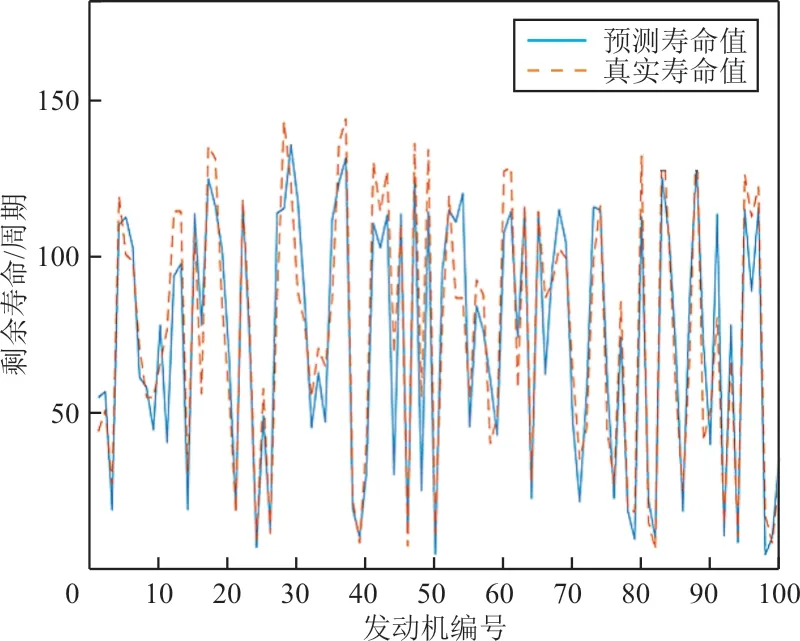
图6 模型预测结果Fig.6 Model prediction results
为了进一步验证所建立模型的预测效果,对C-MAPSS数据集的FD003中1、9、24、35号发动机剩余寿命进行预测拟合,其中部分发动机数据拟合结果如图7所示。
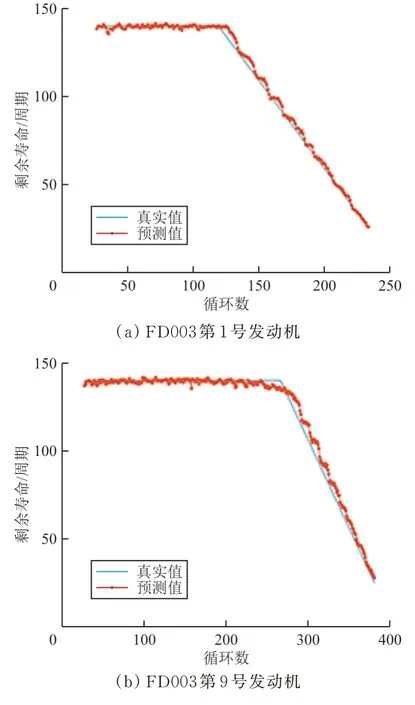
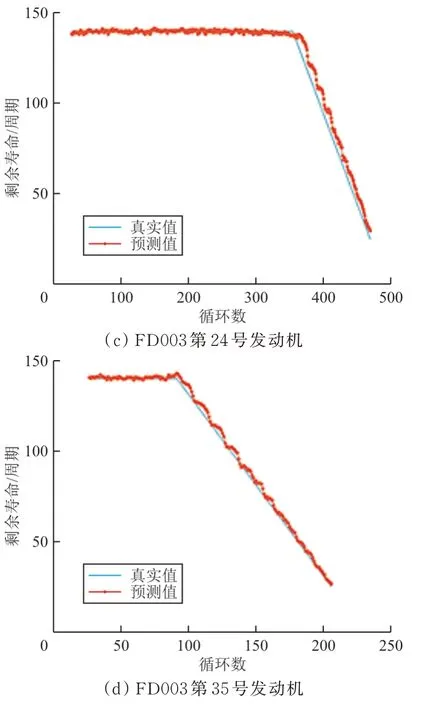
图7 不同型号发动机预测对比Fig.7 Comparison of predictions for different types of engines
从图7可以看出:无论发动机处于循环周期的前、中、后期,该模型得到的预测值和真实值的拟合程度都较为准确,预测值分布在真实值附近。由此可以得出本模型针对发动机这类复杂设备具有较高的预测精度,为提升发动机的可靠性和安全性提供了依据。
3.3 多模型预测结果对比
为了证明模型的准确度,选用FD003中1号发动机数据,分别搭建支持向量机回归(SVR),CNN,LSTM以及BLSTM预测模型,并与KPCABLSTM预测结果相对比,对比结果如表3所示。

表3 多模型预测结果对比Table 3 Comparison of multi-model prediction results
从表3可以看出:KPCA-BLSTM模型在误差和得分上均优于单个模型,三种深度学习模型预测结果优于传统机器学习方法SVR;BLSTM比LSTM具有更好的性能,这表明BLSTM在处理较长时间序列时可以结合历史和将来的信息来充分表征状态监视数据的内部关系。
4 结论
(1)利用KPCA对航空发动机多监测信息进行降维与融合,通过方差贡献量判断10维为最佳目标降维量,最终得到一个低维信息融合数据集。
(2)搭建了BLSTM神经网络预测模型,利用经信息融合后的数据集对其进行训练,最终模型预测值对真实值拟合程度较高,表明模型的预测效果较好。
(3)选取所提出的剩余寿命预测模型,将预测结果与SVR、CNN以及双向LSTM预测模型进行对比,KPCA-BLSTM模型的均方根误差与得分皆优于其他三种模型。
