液压缸用外置式磁感应位移传感器设计*
2022-06-23樊烨男廉自生
樊烨男,高 飞,廉自生
(太原理工大学 机械与运载工程学院,山西 太原 030024)
0 引 言
电液伺服系统既具有液压系统的优势,又拥有电子系统的可控性能,使得其在采矿、机械制造等领域得到了广泛应用。
液压缸作为电液伺服系统的关键执行元件,其高精度、高可靠的位移检测要求一直推动着测量技术的发展,各式各样的位移传感器也随之出现。
近年来,较多学者对液压缸位移检测技术进行了研究。李学胜等人[1,2]基于磁致伸缩原理设计了适用于液压缸的位移传感器,其测量精度高、量程大;但该类传感器结构复杂,需在活塞杆加工出深孔放置波导杆,对工艺要求较高,并且还涉及到传感器的耐高压问题,成本也很高。张文杰等人[3,4]利用磁环控制干簧管通断,将位移转变为电压信号,实现了液压缸位移检测;但其测量精度受干簧管排列间隙影响,且抗振动差,干簧管易碎裂,检修困难。陈陆曦等人[5,6]通过将活塞杆表层制成凹凸相间结构,实现了对永磁体磁力线的周期调制,使活塞杆具有标尺功能,达到了类磁栅的检测效果;但是采用该方法得到的输出信号过于微弱。李志宾等人[7]通过重新设计调理电路,提高了信号的输出质量;但其电路过于复杂,成本也比较高昂。
以上研究针对的是液压缸内置式位移传感器,因而具有传感器安装工艺复杂、检修困难等问题。
随着磁感应技术的日趋成熟,PERIS C等人[8-13]使用霍尔或磁阻传感器实现了位移测量,但大多数研究者都是利用工作在磁场饱和区的各向异性磁电阻(anisotropic magneto resistive,AMR),通过测量磁场角度来判断位移量。
基于以上研究,笔者设计一款外置式磁感应位移传感器,利用工作在非饱和磁场的TMR磁阻元件[14]检测活塞永磁环运动时缸筒外部磁场强度的变化来实现对位移的测量,通过仿真模型分析磁场与磁阻的输出信号,为计算永磁环位移提供理论基础,并通过实验对传感器设计的可行性进行验证。
1 传感器构成及原理
液压缸通过液压阀控制进出液,将压力能转化为活塞的动能,继而完成伸缩动作[15]。笔者据此原理设计了传感器测量结构,主要包括活塞永磁环、外置磁感应位移传感器两部分。
传感器结构如图1所示。

图1 传感器结构
1.1 活塞永磁环
笔者通过在活塞处安装永磁环,将活塞的位移转化为永磁环的位移。
永磁环安装方法如下:首先在活塞表面加工出与永磁环尺寸相同的凹槽,随后将非导磁材料,如工业陶瓷等均匀填入凹槽内,确保工作时不产生液体泄漏,同时减弱活塞的导磁作用,最后将永磁环嵌入凹槽内即可。
永磁环结构如图2所示。

图2 永磁环结构
永磁环由两个径向充磁、尺寸相同的钕铁硼磁环组成,两侧会产生强度相同、方向相反的规律磁场,相比单个磁环,该结构更有助于提高测量位移的精度。
1.2 外置磁感应位移传感器
由于缸筒为导磁材料,液压缸外部磁场强度较弱,磁阻元件选用多维公司生产的TMR9002磁阻元件,如图3所示。

图3 TMR9002磁阻元件
该磁阻元件在正向磁场下产生正向输出电压,输出与磁场强度成正比,非线性度0.5%,灵敏度100 mV,且具有优越的温度稳定性,无需进行温度补偿,抗电磁干扰能力强、精度高,满足使用要求。
磁场检测由直线排列的多个磁阻元件完成,与电路板一起封装在非导磁外壳内,传感器整体平行于活塞杆安装在液压缸缸筒外部,其轴线与永磁环充磁方向垂直。当永磁环发生位移时,缸筒外部磁场强度产生变化,磁阻元件将检测到的磁场信号转换为电压信号,输送至信号调理电路,通过单片机计算出永磁环位移。
相较以上几种研究,该传感器结构更为简便,检修难度更小,且永磁环使用寿命长、稳定性较高,无需经常更换。
2 传感器电路设计
电路的主控制器需满足采集频率高、计算功能强大等条件,笔者在设计中选用STM32系列单片机,该系列单片机内置32 K~128 K的闪存,时钟频率36 MHz~72 MHz,能够快速实现大量数据的采集、存储、处理功能[16]。
传感器电路图如图4所示。

图4 传感器电路图
笔者以8个TMR9002磁阻元件为一组进行信号采集,每组共输出16路差分电压信号,两个多路选择开关的使能端INH与通道选择端a,b,c由单片机进行逻辑控制,同时选通某一个磁阻元件的两路输出;
因磁阻元件输出幅值较小,为便于单片机电压信号采集,需使用差分比例电路对信号进行放大处理,用2.5 V基准源与运算放大器组成偏置调节电路,通过调节电阻比例来调节偏置信号的大小,信号经放大与偏置后,利用电压跟随器接入A/D采集接口,并使用单片机对A/D的转换进行控制。
3 传感器仿真分析
3.1 仿真模型
基于Ansoft Maxwell电磁仿真软件,笔者建立了传感器测量系统有限元模型,其中,液压缸结构与永磁环磁场分布基本对称,对模型做了轴对称处理[17]。
传感器仿真模型如图5所示。
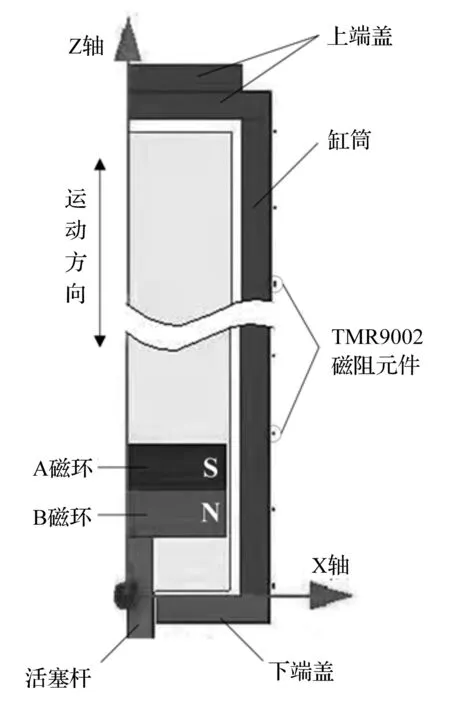
图5 传感器仿真模型
模型的主要参数如下:液压缸长600 mm,活塞行程560 mm,缸筒厚度15 mm,磁导率500 H/m,永磁环外径110 mm,内径60 mm,A、B磁环高为25 mm,沿X轴方向充磁,材料为NdFe35钕铁硼,矫顽力HC为-8.9×105A/m,磁阻元件根据TMR9002传感器实际参数设置,沿缸筒外壁直线排列,间隔相等,数量若干。为方便后续描述,将永磁环分为A、B磁环表示。
仿真选用瞬态磁场求解器,其矢量磁位A满足的场方程如下:
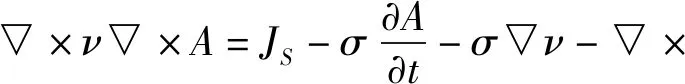
(1)
在以永磁环自身坐标分析时,偏时间导数变成全时间导数,运动方程为:
(2)
式中:HC—永磁体的矫顽力;ν—永磁环的运动速度;A—磁矢位;JS—源电流密度。
设置运动的时间步为0.5 s,终止时间50 s,运动速度ν=11.2 mm/s,求解器便可根据式(1,2)解算出有限元模型任一时间段内任一点的磁场强度。
3.2 磁场分析
永磁环运动至25 s时,其附近区域的磁通密度云图和磁力线分布图如图6所示。
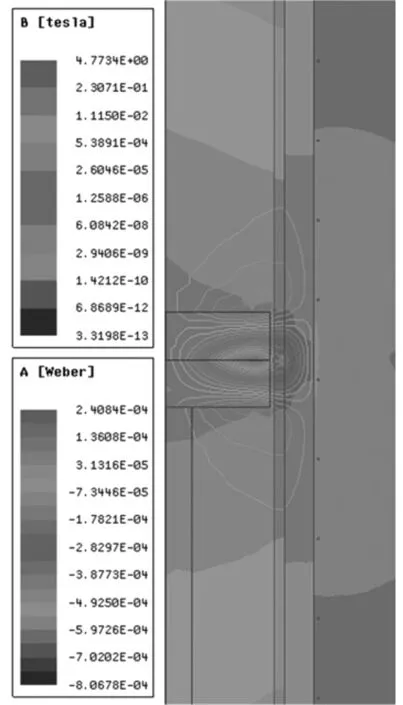
图6 磁通密度云图与磁力线分布图
从图6可以看出:在永磁环附近,由于缸筒的导磁作用,液压缸内部磁场强度明显高于外部磁场,但缸筒外仍有部分漏磁,满足磁阻元件的检测要求;永磁环外磁路共有3条路径,方向分别为A磁环N极到A磁环S极,B磁环N极到A磁环S极,以及B磁环N极到B磁环S极;磁力线在A磁环的S极和B磁环的N极处最为密集,此处磁场强度最大,且由两磁极向两端逐渐减小;在永磁环上下两侧,磁力线形状基本相同,两侧磁场强度相等,方向相反,由此可推测,在永磁环经过某一磁阻元件时,其输出信号应为关于某点近似对称的曲线。
3.3 输出信号分析
笔者以未经信号电路处理的传感器输出信号进行分析,单个磁阻元件的输出曲线及位置示意图如图7所示。
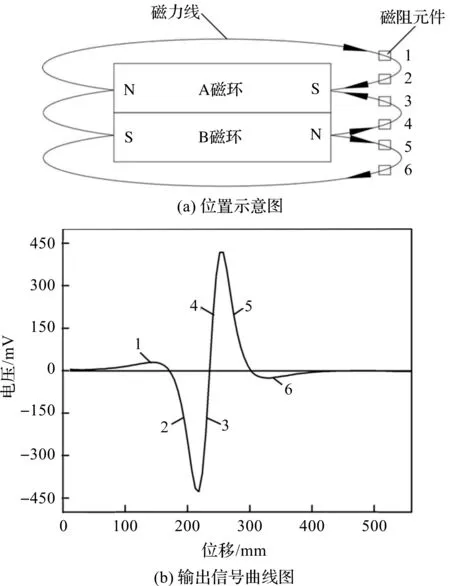
图7 单个磁阻元件输出曲线及位置示意图
图7(a)中:1~6表示磁阻元件与永磁环的相对位置,箭头表示磁场方向。永磁环由远及近靠近磁阻元件时,磁阻元件首先处于1位置,磁场方向为正,此时磁阻元件距离永磁环磁极较远,输出幅值较小,对应图7(b)中的1段曲线;
磁阻元件处于2,3位置时,靠近A磁环S极,磁场方向为负,磁场强度先增大后减小,输出幅值较大,达到负向峰值,对应2,3段曲线;
磁阻元件处于4,5位置时,靠近B磁环N极,磁场方向为正,磁场强度先增大后减小,达到正向峰值,对应4,5段曲线;
当永磁环远离该磁阻元件时,元件处于6位置,磁场方向为负,输出幅值较小;
曲线各零点表示磁场方向与磁阻元件的敏感方向垂直时元件输出为0,其中,两峰值间的零点表示磁阻元件位于A、B磁环连接处。曲线正、负峰值相等,关于3,4段曲线零点近似对称,与磁场分析结果一致。
3.4 位移计算方法
由图7可知,正、负峰值间曲线线性度较高,该段曲线为磁阻元件的有效线性工作区,笔者采用多个磁阻元件的有效线性工作区叠加的方式来测量永磁环位移。
单片机计算永磁环位移的程序逻辑如下:
(1)前提条件。永磁环作全量程位移,对各位置磁阻元件输出信号进行采集,完成数据初始化,因单片机采集到的信号经过放大与偏置,需将信号还原,使程序根据磁阻元件的初始输出数据进行判断;
(2)一组磁阻元件的初始输出如图8所示。

图8 一组磁阻元件初始输出
(3)完成初始化后,测量开始。当永磁环运动至该组传感器测量范围时,单片机采集到8路磁阻元件的初始输出信号,即U1—U8;
(4)确定永磁环的位移区间。将a、b零点之间的距离以其他曲线峰值之间的零点为界限分为7个小区间,永磁环运动至c段区间时,U4为正,U5为负,同理,永磁环位于其他区间时,相邻两个传感器元件输出正负不同,因此当程序判断Ui>0,Ui+1≤0时,便可确定永磁环所处区间;
(5)将(0,0),(d,Ux)两点代入y=ax+b中,求得每个元件的线性公式,其中Ux为Ui+1=0时Ui的取值,d为两相邻磁阻元件的间隔距离;
(6)将Ui代入永磁环所在小区间的线性公式,即可解得永磁环在该小区间的位移。
总位移表达式为:
L=d×(i-1)+Lx
(3)
式中:L—永磁环的总位移;Lx—永磁环在小区间内的位移。
每组元件测量范围为a零点至b零点,量程7×dmm,多组元件工作时总量程为:(N-1)×d,N表示磁阻元件总数量,安装时,首个磁阻元件的安装位置需与永磁环位移为零时A、B磁环的连接处平齐。
为得出磁阻元件的最佳间隔距离d,引入线性度的概念。线性度即非线性误差为实际输出曲线和拟合直线之间的偏差。其计算公式为:
(4)
式中:δ—线性度;ΔUmax—最大非线性绝对误差;U—输出满量程,即两峰值的差值。
以0.5 mm为增量,笔者通过MATLAB软件求出元件间隔d为9 mm~14 mm时,线性公式对应曲线的线性度以及误差小于1 mm时曲线的线性度要求,如表1所示。

表1 不同间隔时曲线线性度
由表1可知,随着间隔距离d增大,曲线线性度逐渐减小,间隔距离为12.5 mm时,曲线线性度刚好不超过误差小于1 mm时的线性度要求。
因此,在满足线性度要求的前提下,为避免间隔距离过小,造成磁阻元件的浪费,笔者选择元件间隔距离d=12.5 mm。
3.5 缸筒对检测结果影响
笔者通过改变缸筒磁导率和厚度参数研究了缸筒变化对磁阻元件输出信号的影响。磁场强度超过TMR9002的工作范围时,选用其他型号的TMR磁阻元件。
缸筒材料一般为铸铁、铸钢等,铸铁磁导率为200 H/m~400 H/m,铸钢稍高一些,常用的45号钢磁导率可达600 H/m,不同处理方式下材料磁导率不同,但大都不超过1 000 H/m[18]。
笔者以缸筒厚度15 mm为前提,将磁导率μ分别设为50 H/m,100 H/m,200 H/m,500 H/m,1 000 H/m,得到不同磁导率下磁阻元件的输出信号曲线,如图9所示。

图9 不同磁导率下输出信号
通过图9可知:当磁导率取值逐渐增大时,磁阻元件输出幅值明显降低,正、负峰值由4 000 mV降至200 mV。5条曲线的变化趋势相同,各零点与取得峰值的位置未变化。
以磁导率500 H/m为前提,笔者将厚度h分别设为15 mm,20 mm,25 mm,30 mm,得到不同厚度下磁阻元件的输出信号曲线,如图10所示。
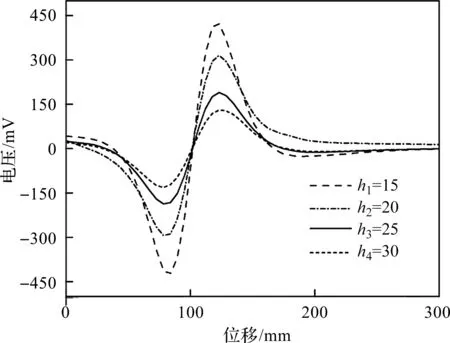
图10 不同厚度下输出信号
通过图10可知:当缸筒厚度逐渐增加时,传感器元件输出幅值降低,正、负峰值由420 mV降至130 mV。各曲线变化趋势相同,正、负峰值间零点与取得峰值的位置未变化,但缸筒厚度改变会使磁路路径发生变化,因此,正、负峰值前后零点位置均有较小变化。
结合图9、图10,缸筒磁导率与厚度变化时,磁阻元件的有效线性工作区对应位移区间长度不变。因此,检测缸筒材料与厚度不同的液压缸时,完成数据初始化后,无需改变磁阻元件的间隔,仍可按照原有程序参数计算位移,提高了传感器的使用效率。
4 实验测试
由位移计算的方法可知,磁阻元件输出两峰值间曲线的线性度是影响传感器测量精度的关键因素,因此,笔者利用实验装置对磁阻元件实际输出曲线的线性度进行分析。
实验装置如图11所示。

图11 实验装置
除缸筒磁导率外,各项参数与仿真模型一致,活塞杆带有精度1 mm的刻度尺,单片机液晶显示器显示磁阻元件的电压输出。
笔者使液压缸作全量程位移,每5 mm对液晶显示器的数值进行记录,重复测量3次,求各点的输出平均值。
笔者将其中一个磁阻元件的数据绘制成曲线图,并和理想的线性拟合曲线进行对比,如图12所示。
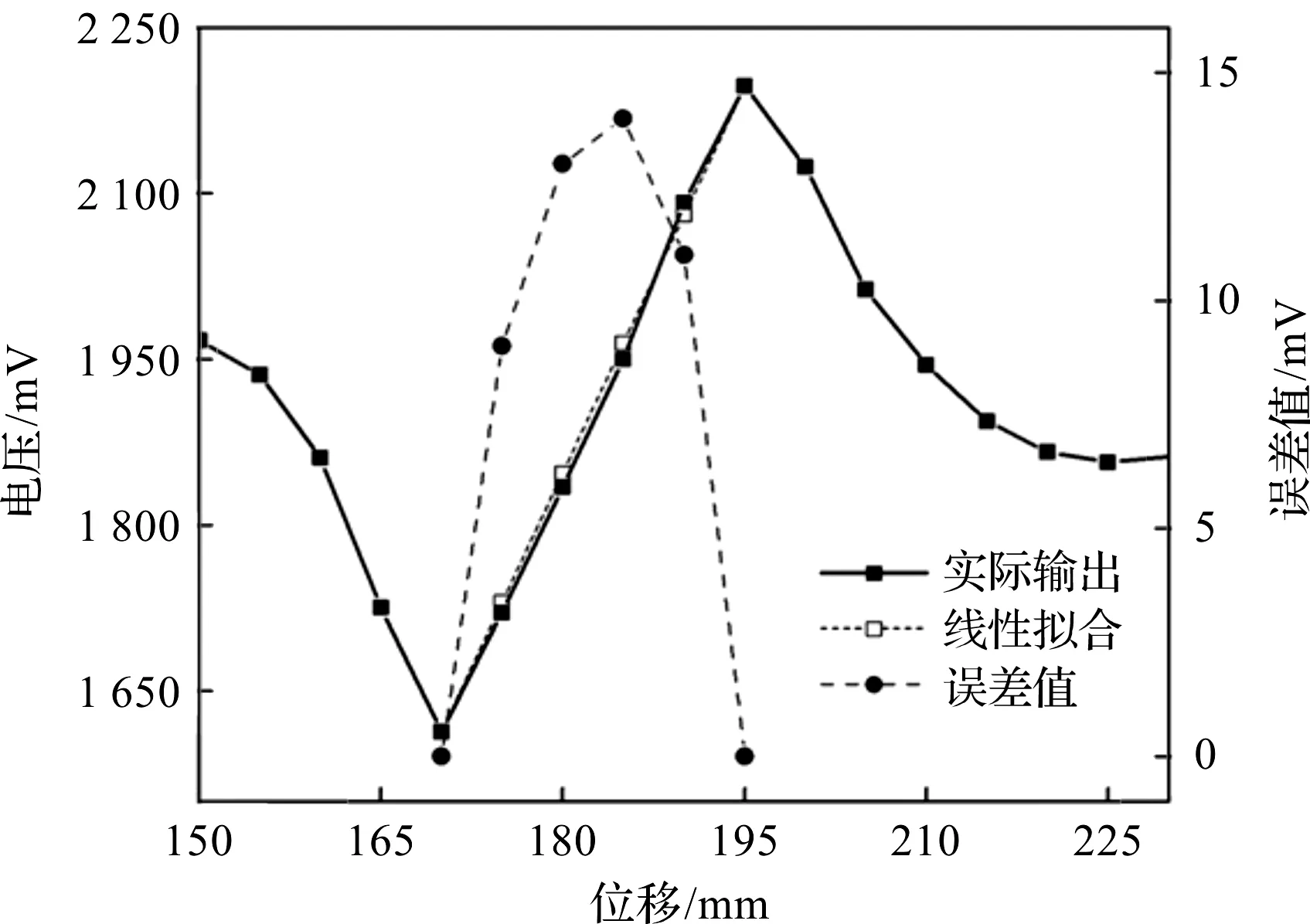
图12 磁阻元件的线性度
通过图12可知:输出满量程为584 mV,最大非线性绝对误差为14 mV,根据式(4)求得该磁阻元件线性区域的线性度δ=2.39%。线性区域对应位移区间长度25 mm,因此,永磁环每移动1 mm磁阻元件产生23.36 mV的电压输出,由此得出,当线性区域的最大非线性误差不超过23.36 mV,即线性度不超过4%时,传感器理论测量误差小于1 mm,精度可达0.16%,该磁阻元件线性度满足要求。
传感器位移测量结果是由单片机根据磁阻元件输出的电压信号计算得出,在该方法中,输入量为磁阻元件电压信号,其最小变化单位为1 mV,输出量为永磁环位移量。在该磁阻元件的线性区间内,每相邻两个采样点之间的曲线斜率不同,计算传感器分辨率时,应采用使输出量产生阶跃变化的输入量中的最大变化值即斜率最小的一段曲线作为衡量指标。
由图12可以求得,在斜率最小的曲线段内,每1 mV电压变化对应永磁环位移为0.045 mm,即该磁阻元件可分辨的最小位移为0.045 mm,考虑各磁阻元件的差异性,传感器整体可分辨的最小位移可达0.05 mm,传感器量程600 mm,分辨率为0.008 3%。传感器灵敏度由单片机程序设定,可通过改变程序参数调节灵敏度数值大小。
为验证传感器的重复性,笔者在该磁阻元件的线性输出区域,即170 mm~195 mm范围内,测试永磁环不同位置下元件的电压信号。
试验3次后,得到测试的结果如图13所示。
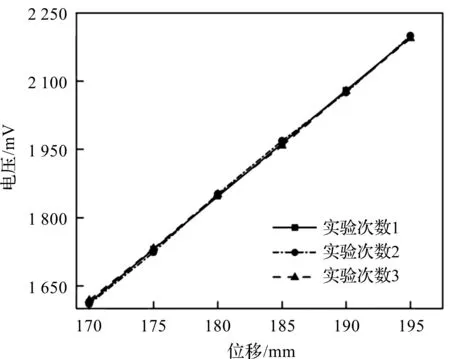
图13 磁阻元件重复性测试结果
由图13可知,3次实验磁阻元件输出信号的重复误差较小,所设计的传感器重复性较好,能够确保其在实际测试系统中的使用。
5 结束语
笔者设计了一款液压缸用外置式磁感应位移传感器,运用Ansoft Maxwell软件分析了其工作磁场及磁阻元件输出信号,基于分析结果提出了位移计算方法,研究了缸筒磁导率和厚度对测量结果的影响,并通过实验对仿真结果及传感器各项性能指标进行了验证分析。
研究结论如下:
(1)传感器磁场分布规律与磁阻元件输出信号变化规律一致,符合永磁环双环结构的设计预想;
(2)磁阻元件排列的最佳间隔距离为12.5 mm,缸筒磁导率与厚度变化不改变磁阻元件的有效线性工作区对应位移区间的长度,因此,传感器可直接测量缸筒材质与厚度不同的液压缸;
(3)通过实验求得,磁阻元件实际输出曲线的线性度为2.39%,满足测量误差小于1 mm对线性度的要求,精度为0.16%,可分辨的最小位移为0.05 mm,分辨率为0.008 3%,具有良好的重复性。
在后续的研究当中,笔者将对永磁环尺寸对传感器测量结果的影响进行分析,并不断提高磁阻元件输出信号的线性度,优化位移算法,提升磁感应位移传感器的各项性能指标,争取早日实现其产品化。
