基于机器学习和测井数据的碳酸盐岩孔隙度与渗透率预测

2022-06-23侯贤沐王付勇廉培庆

吉林大学学报（地球科学版） 2022年2期

侯贤沐，王付勇，宰芸，廉培庆

1.油气资源与探测国家重点实验室，北京 102249 2.中国石油大学(北京)非常规油气科学技术研究院，北京 102249 3.中石化石油勘探开发研究院，北京 100083

0 引言

在评价储层和评估油气储量时，测井数据具有十分重要的意义。可根据测井数据推断储层构造，构建相应油藏地质模型。传统过程需要基于专家经验，根据经验公式、岩石物理实验、地质沉积构造等方法综合考虑，效率低，人为误差较大。在当前数据驱动方法快速发展的背景下，将测井数据与机器学习相融合，实现测井数据的自动智能解释与分析是未来发展的趋势[1]。

孔隙度和渗透率是油藏储层关键的物性参数。通过取心井获取储层天然岩心，通过实验室测定孔隙度、渗透率等参数，是获取储层物性参数最为准确方法，然而，取心井取心的缺点是耗时长、成本高。虽然有许多物理方法可预测孔隙度和渗透率，比如传统的线性回归方法及数字岩心等效分形介质模型预测方法[2]，但是这些物理方法预测过程繁琐或者预测条件局限性较大。基于机器学习分析测井曲线与钻孔中各地层物性参数、岩性以及沉积规律之间的关系和特征响应模式，为测井数据处理分析提供了新的解决途径[3-5]。

前人基于机器学习，利用测井数据对储层孔隙度和渗透率等物性参数进行预测。崔学慧等[6]基于声波时差(DT)、自然电位、自然伽马(CGR)、地层真电阻率(Rt)4种测井曲线，采用随机森林(RF)回归算法预测孔隙度，预测效果远好于线性回归预测。K-近邻(KNN)方法在聚类分析方面具有突出的优势，多应用于地层属性识别及油田数据分类[7-10]，而较少应用于渗透率和孔隙度的回归预测，但本文也将尝试利用KNN方法进行储层孔隙度与渗透率预测。袁伟等[11]根据测井数据划分储层类型，分别建立了各类储层的渗透率预测模型，利用支持向量机(SVM)方法对每类储层进行训练学习，发现分类后的预测精度较分类前有明显提高。用传统SVM方法预测孔隙度与渗透率时，SVM高斯核函数中的参数对SVM学习预测性能的影响较大。当样本量较小时，SVM回归模型对孔隙度和渗透率样本群体的大小不敏感；当样本量较大时，预测拟合准确度又不高。最近几年，遗传算法和粒子群算法普遍应用于机器学习参数的选择优化，SVM回归得到进一步的发展[12-14]。Elkatatny 等[15]建立了一个人工神经网络(ANN)模型，并基于Rt、岩性密度(RHOB)和补偿中子(NPHI)3种测井数据预测非均质碳酸盐油藏的渗透率，得到一种数学方程，节省了预测时间并提高了预测渗透率精度。Ahmadi等[16]采用的数据样本包括DT、NPHI、RHOB和总孔隙率，依据模糊算法或粒子群算法，结合机器学习的预测效果突出。张东晓等[17]研究测井曲线生成方法时发现长短期记忆(LSTM)方法能够更有效地从训练数据中提取信息，即使训练数据较少，LSTM仍然可以实现有效训练。武中原等[18]基于LSTM，以CGR、光电吸收截面指数(PE)、RHOB、DT、NPHI和Rt等6种测井参数为输入参数，构建了岩性识别模型，与传统方法相比，LSTM方法岩性识别准确率更高。

目前研究主要针对储层物性较好的砂岩油气藏，而对非均质性更强、裂缝与溶孔广泛发育的碳酸盐岩油藏研究较少。基于中东某碳酸盐岩油藏测井数据，选取4种不同的机器学习方法(RF、KNN、SVM、 LSTM)预测储层孔隙度与渗透率，并与取心实验测试孔隙度与渗透率对比，筛选最优机器学习方法，以期实现碳酸盐岩储层孔隙度、渗透率智能准确预测。

1 机器学习方法

1.1 随机森林

RF[19]是一种以决策树为基础的集成学习算法，算法核心是Bagging思想[20]和随机子空间法[21]。输入样本，RF将内部多个决策树的预测结果取平均得到最终的结果。能够进行非线性反演，对高维特征数量具有很好的预测效果。此外，RF还具有操作简单、易于实现、不易过拟合、计算效率高等优点。

1.2 K-近邻

KNN回归预测方法是对连续的数据标签进行预测，依据计算数据点最临近的k个数据点平均值而获得预测值。

1.3 支持向量机

SVM的基本思想是通过核函数将样本空间映射到一定维度的特征空间，在特征空间中求出原样本的最优分类面，得到输入变量和输出结果之间的一种线性或非线性关系，即寻找SVM进行模式分类。而SVM回归是SVM中一个重要的应用分支，主要是通过升高维度后，在高维空间中构造线性决策函数来实现线性回归。通过引进核函数，既能升高维度，又能控制过拟合。同时，核函数代替线性方程中的线性项可以使原来的线性算法“非线性化”，实现非线性回归。核函数种类有很多种，如线性核、多项式核、Sigmoid核和径向基函数(RBF)核。由于特征数据维度较高，本文选用RBF核函数：

(1)

式中：K为核函数；x、y为特征向量；γ为核参数。

1.4 长短期记忆网络

LSTM由Hochreiter等[22]于1997年首次提出，经过后续发展，形成当今应用广泛的机器学习算法。LSTM是对常规循环神经网络(RNN)的一种改进和完善，加入了遗忘层、输入层、输出层结构，能保留跨度较大序列中的有用信息，解决了RNN单元结构中一个tanh层下部分信息相关性低下的问题，避免了常规RNN中出现的梯度消失、梯度爆炸等问题。LSTM是目前应用最成功的RNN网络之一。

图1是经典的LSTM重复单元，核心公式如下：

it=σ(Wixt+Wiht-1+bi)；

(2)

ft=σ(Wfxt+Wfht-1+bf)；

(3)

ot=σ(Woxt+Woht-1+bo)；

(4)

gt=tanh(Wgxt+Wght-1+bg)；

(5)

ct=ft⊗ct-1+it⊗gt；

(6)

ht=ot⊗tanh(ct)。

(7)

式中：Wi、Wf、Wo和Wg分别为输入门、遗忘门、输出门和待选记忆细胞的权重参数；bi、bf、bo和bg分别为输入门、遗忘门、输出门和待选记忆细胞的偏置项；t为时刻。

σ. sigmoid非线性激活函数；ct-1、ct. 前一序列、当前序列隐藏层节点状态；ht-1、ht. 前一序列、当前序列隐藏层节点输出；xt. 当前序列隐藏层节点输入；it. 输入门；ft. 遗忘门；ot. 输出门；gt. 待选记忆细胞；⊗、⊕. 矩阵对应位置元素相乘、相加。

图1 LSTM单元结构图

Fig.1 LSTM unit structure diagram

由式(5)经过tanh激活，得到gt，通过式(6)和式(7)得到ct和ht。循环计算时，权重参数将不断变更，每次都会输出得到的一个ht和ct，通过投影矩阵解码出对应的值。

2 现场应用实例

中东某碳酸盐岩油藏主力含油层系为白垩系F、S组，均为碳酸盐岩沉积。S组沉积范围为2 700～3 400 m，厚度约为680 m；F组沉积范围为4 000～4 500 m，厚度为400～450 m。以F层测井参数作为研究对象开展研究。如表1所示，共有8口取心井，计914块岩心在实验室测定孔隙度与渗透率，取心深度为4 072.84～4 404.03 m。对原始测井数据进行筛选，选取CGR、无铀伽马(SGR)、PE、Rt、DT、RHOB和NPHI 等7种测井数据，通过机器学习方法预测储层孔隙度与渗透率。A1井的139组数据用于预测集，其余7口井的775组数据作为训练集。

表1 各取心井取心数据统计

建立数据库(8口取心井的孔隙度和渗透率)，采用min-max标准化方式消除不同测井数据量纲的影响：

(8)

式中：x为测井参数原始值；x*、xmin、xmax分别为x的归一化值、最小值、最大值。

本文展示了以A1井孔隙度为例的部分标准化样本数据(表2)。

基于Python编程语言实现RF、KNN和SVM算法，基于MATLAB编程语言实现LSTM循环神经网络算法，训练预测过程如图2所示。

因为均方根误差(RMSE)能够表示真实值与预测值之间存在的误差，故选取RMSE作为评判预测效果的指标。同时，采用统计学中的判定系数(R2)作为辅助评判指标，其值越大，预测值越接近真实值。

2.1 孔隙度预测

使用Python编程语言，调用sklearn库，调试超参数，基于RF、KNN和SVM预测孔隙度。

实现基于RF预测孔隙度的过程如下。第一步，输入样本集，从初始样本集中有放回地随机抽取固定数量样本，进行T轮采样，得到T个训练集。

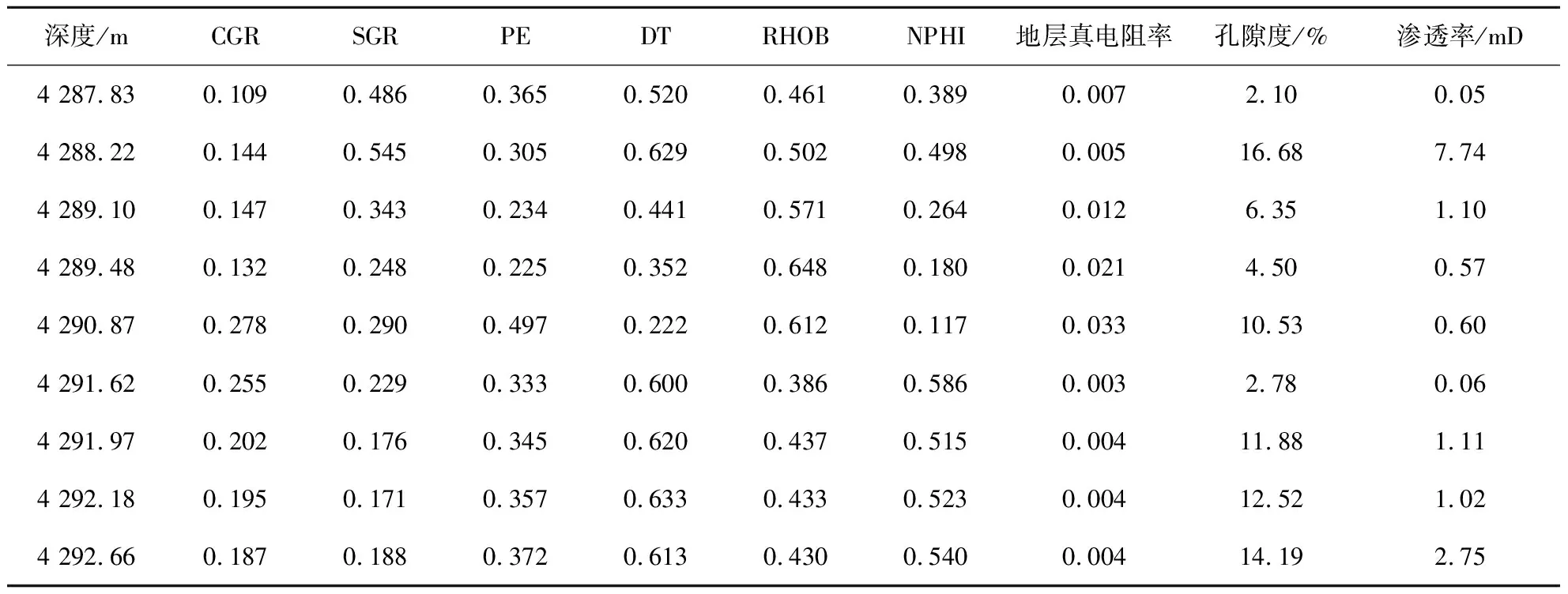
表2 A1井部分标准化样本数据以及对应孔隙度和渗透率

图2 基于机器学习的储层孔隙度和渗透率预测流程图

第二步，决策树选择最优属性的节点分裂。在这个过程中，每一个训练集全部子集属性等概率被选择，且每个样本训练子集相互独立，最后生成T个决策树，T个决策树预测结果的均值作为最终的预测结果。反复实验，最终确定本次回归RF核心参数决策树数量为90个。

实现基于KNN预测孔隙度过程主要为k值选取。根据经验k一般取10，样本数据量小的时，k可以适当调大。反复训练模型，当KNN核心参数k为13时，预测效果达到最优。

SVM选取核函数为RBF，根据sklearn官网给出惩罚因子与核参数γ的关系。结合实践，在10-3～103的对数范围内选取惩罚因子即可满足预测精度，因此从10-3开始，最终选取合适的惩罚因子为100，γ为0.01，得到SVM模型最好的评价指标。

使用MATLAB编程语言，调试超参数，实现LSTM预测孔隙度。将7种测井参数作为输入参数，创建具有3个隐藏层的神经网络。优化每层神经元数，隐藏层节点数必须小于m-1(m为训练样本数量)。m必须大于网络模型参数数量，一般是其2～10倍。基于本文训练样本为775组，神经元总数应在70～400之间，逐步调整超参数合理数值，得到LSTM模型最优评价指标，最终设置第1层、第2层、第3层隐藏层神经元数分别为85、75、65。选用Adam优化算法代替经典的随机梯度下降法，其优点是可以有效更新网络权重，自动调整学习率。批量大小设置为20，初始学习率为0.01，进行200次训练。因每次随机生成的权重参数不同，生成的损失函数可能不收敛，则需再次训练，直至水平收敛即可。为了达到理想结果，预测集重复预测5次，最终选取RMSE评价指标最高的预测模型。

孔隙度预测均基于以上设定。由于机器学习方法在机器学习拟合过程中起主导作用，超参数只起到基本调节作用，改善精度效果不明显，因而免去重复调节超参数的过程，继续后续研究，以提高本次研究的效率。

图3给出了A1井测井参数与实际孔隙度的相关性，其中NPHI与孔隙度相关性最高，其余测井参数与孔隙度相关性从高到低依次为RHOB、DT、PE、Rt、SGR和CGR。

依据图3中的相关性顺序，进行特征消除选择。首先删除相关性最小的特征值CGR，输入其余6种参数，利用机器学习方法训练模型；进一步删除SGR测井数据，输入剩余5种测井数据训练模型；后续依次删除Rt、PE、DT和RHOB数据，直至剩余NPHI的数据为止。统计RF、KNN、SVM、 LSTM 4种机器学习方法的RMSE，结果如图4所示。当NPHI、RHOB和DT 3种测井参数数据作为输入时，LSTM方法的RMSE值最低，说明预测精度最高；而且LSTM方法较其他3种机器学习方法，输入不同参数时，预测精度普遍更高。

在输入NPHI、RHOB、DT 3种参数数据的条件下，分别采用RF、KNN、SVM和LSTM方法预测孔隙度，预测值与真实值对比见图5。从图5可以看出，孔隙度小于5%或大于20%的范围预测偏差较大。这些真实孔隙度在整个底层段是两个极端方向的值，预测值有所偏差是正常的，整个预测值与真实值的走势大致相同，达到了预期目的。因此，选取合适的测井参数对提高孔隙度预测效果至关重要。

表3为RF、KNN、SVM、LSTM方法NPHI、RHOB、DT 3种参数预测A1井孔隙度的RMSE和R2，可以看出：LSTM方法的RMSE最低，其值为4.536 2，R2为0.577 2，说明采用LSTM方法预测结果最好；相较其他方法，RF方法的RMSE最高，达到了5.356 3，说明RF方法不太适合预测拟合孔隙度。

2.2 渗透率预测

分别采用LSTM、RF、KNN和SVM方法进行渗透率预测。首先给出A1井7种测井数据与实际渗透率半对数相关性，如图6所示。从图6可以看出：因渗透率与测井参数相关性特征选择顺序有所变化，输入参数种类改变，需依次剔除CGR、Rt、SGR、DT、PE和RHOB测井数据，训练各自模型，评价最优模型。基于渗透率的测井参数选择，LSTM方法3个隐含层参数依次设置为90、75和70，其他程序条件未作变动。最终统计结果见图7，可见4种方法拟合预测值与真实值偏差均较大。表4为4种机器学习方法仅输入NPHI参数预测A1井渗透率的误差，其中：RF方法最好，预测结果的RMSE为45.882 3，R2为0.407 3，效果仍不理想；KNN、SVM和LSTM方法预测偏差同样较大，SVM预测模型的R2甚至出现负值，这与实际情况相差甚远。究其原因，主要有以下两点影响因素：第一，碳酸盐储集层储集空间类型多、次生变化大这些差异导致岩心完整性不好，影响整个层位实验参数的代表性；第二，测试岩样体积特别小，所测得渗透率不能反映整个层位的性质，当碰到碳酸盐岩这类非均质性较强的储层时，微裂缝和孔洞广泛发育，测井曲线精度会影响机器学习预测的准确性。

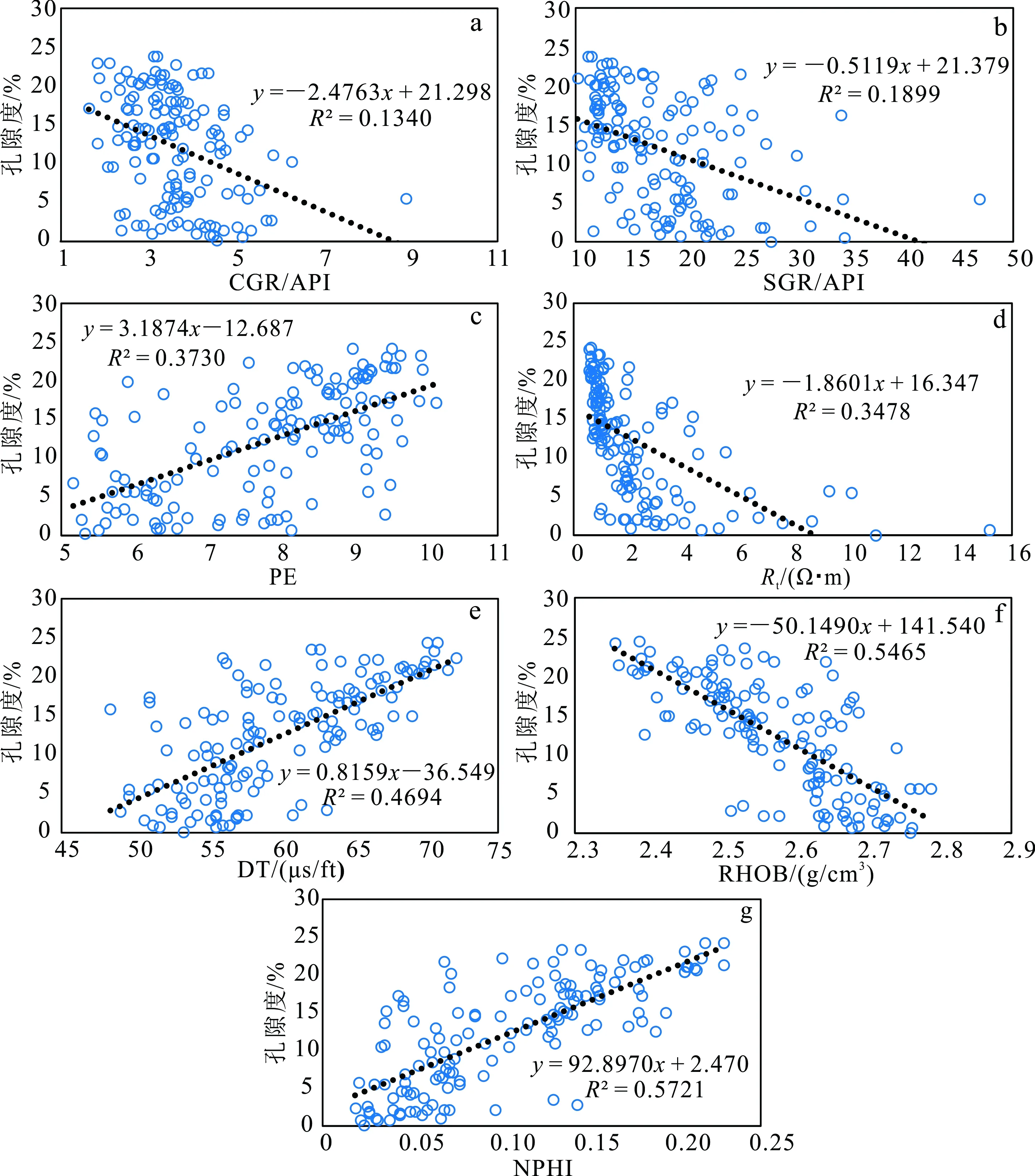
ft(英尺)为非法定计量单位，1 ft=0.301 8 m，下同。

图4 基于孔隙度相关性特征参数选择输入的RMSE变化值

表3 4种机器学习方法预测孔隙度误差和判定系数

NPHI与渗透率相关性最高，其余测井参数与渗透率相关性从高到低依次为RHOB、PE、DT、SGR、Rt和CGR；相较于孔隙度与测井参数数据的相关性，渗透率与测井参数数据的相关性表现较差，说明储层渗透率比孔隙度难于表征。

图5 基于RF(a)、KNN(b)、SVM(c)和LSTM(d)方法的预测值与真实值对比图

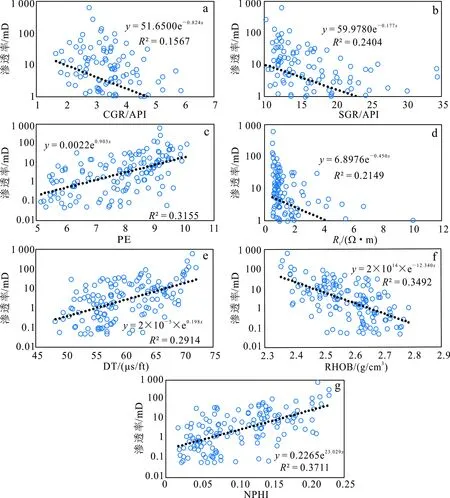
图6 A1井7种测井数据与实际渗透率半对数相关性图

虽然渗透率模型评价参数表现不理想，图8还是给出了本次渗透率预测精度最高的RF模型预测值与真实值对比图，此时仅输入NPHI参数数据。整个渗透率预测值与真实值的走势相同，特别是深度在4 340～4 380 m之间，真实渗透率走势先上升，然后再下降，模型预测值反映出这个趋势。简而言之，模型预测精度还有很大提升空间，值得进一步研究。