数值优化方法在确定张力计反应时间上的应用性

林鸿州, 郭 怡, 白建帮, 彭建兵

长安大学地质工程与测绘学院，西安 710054

0 引言

在自然界与工程实践中所遇到的土多为非饱和土，非饱和土的基质吸力是影响非饱和土的强度、变形与渗透特性的关键物理量。为了测量非饱和土的基质吸力，学者们开展了大量的试验研究工作，开发出许多吸力的测量方法，如张力计、压力板仪、滤纸法与热传导吸力计等[1-2]。这些方法中，又以张力计可直接且快速地测量非饱和土的基质吸力，并广泛应用于实验室、物理模型与现场试验中[3-6]；在滑坡、泥石流等地质灾害防灾减灾工作中，张力计也常用来监测降雨条件下坡体基质吸力的变化特征，并作为多参数监测预警系统的一环[7-9]。此外，测定非饱和土体渗透系数也需要张力计准确地确定土体基质吸力[10]。

尽管张力计较其他方法可较快且较可靠地测量基质吸力，但其仍需一定的时间，才能使土体的基质吸力经由张力计陶土头传递到张力计内的压力传感器，这一时间即为张力计的反应时间(能合理反映出土体基质吸力所需的时间)，或者称为再平衡时间。这一时间与张力计陶土头型式及其饱和程度、土壤结构和土的渗透系数密切相关[11-13]。因此，也可通过张力计的反应时间与测得土的压力变化特点，推估非饱和土的渗透系数[14]。

此外，如果将张力计应用于非饱和土中水的动态不平衡效应的研究(如动态土水特征曲线的确定等)上，张力计反应时间的快慢对瞬时基质吸力的测量将会产生显著的影响[3, 15]。因此，张力计的选用如不合适，将不能合理地探讨非饱和土中水的动态不平衡效应问题。

一般而言，张力计的反应时间可由张力计所测量的压力读数曲线依经验或半经验图解法近似求得，也可通过设定基质吸力变化率准则[12]或理论公式近似计算出[3, 16-17]。其中，半经验图解法依据张力计与土体基质吸力平衡后，其压力响应曲线近似为线性的特点，通过作图法找出合宜的拟合直线，则该拟合直线的起始点(张力计记录的压力读数曲线段与直线段的分段位置)所对应的时间即为反应时间。显然，半经验图解法的优点是直观，但通过目视判断这一曲线段和直线段之间的分段点，对于压力读数抖动幅值较大的情况(离散性很大的压力读数特征)，不仅不易找出合理的张力计反应时间且耗时也较长。因此，为了避免采用半经验图解法所导致的人为误差，并减少时间成本，本文以不同含水量条件下泾阳黄土、定边黄土以及毛乌素砂土为例，先通过张力计测量其压力响应曲线，再利用数值优化方法确定张力计的反应时间，并以此探讨数值优化方法的实用价值及其局限性，以期提出标准化的张力计反应时间判定方法与操作流程。此外，由于反应时间的快慢是选用适宜张力计的关键所在，因此，也希望通过研究为张力计的选用提供科学合理的依据，以利相关试验的开展。

1 材料与方法

1.1 试验土性

为了使研究成果更具普适性，试验土样采用泾阳黄土、定边黄土以及毛乌素砂土3种，这些土性包括了黏土(CL)、粉土(ML)与砂土(SP)。并依据张力计测量基质吸力的量程范围，制备了3种不同含水量的湿土(砂)、中湿土(砂)及干土(砂)，以了解不同土性、不同含水量条件下，张力计测量读数的变化特点。试验用土的基本物理性质如表1所示。

1.2 试验设备与方法

本文采用土柱试验测定张力计的响应曲线，即依照所需土柱的制样含水量与干密度，在侧壁开孔(张力计安装孔，距底面5 cm)的圆柱管内，用落锤将试验用土分层击实成高10 cm、直径8 cm的土柱，分层击实过程中需注意每个分层界面均需打毛；此外，填土的分层界面不能设在张力计安装孔的高程位置，以防止张力计与土之间产生界面空隙，影响测量结果。土柱制备完成后，用保鲜膜与透明胶带密封土柱顶面与张力计安装孔，并静置12 h以上，使土中水重新分布，处于新的平衡状态。之后，即可开始张力计的测量工作，在张力计安装前，需确保张力计陶土头完全饱和，且其内注满除气水。对于较硬的干土样，可在安装张力计前，先预钻小孔，以避免安装过程中损坏陶土头；而安装张力计也需确保陶土头位于土柱中心点，并一次到位，避免反复挤压拉拔，影响陶土头与土体的接触。此外，土柱在试验过程中需保持密封条件，以减少土中水的蒸发对张力计读数的影响。

试验采用的张力计为METER公司生产的微型张力计T5x，数据采集的时间设为2 s。由于微型张力计陶土头的体积小，具有反应时间快且对压力变化响应更灵敏的特点；因此倘若设置较密的数据采集时间，就可捕捉到更细致的读数响应特征。此时测量读数容易受到其他因素干扰而出现抖动的现象，亦即测量数据的离散程度有可能很高，但可借此特点来分析数值优化方法的实用价值及其局限性。

1.3 数值优化方法与计算方案

如前所述，压力读数曲线段与直线段的分段位置所对应的时间即为张力计的反应时间。因此，如要利用数学方法求取反应时间，需用合适的非线性拟合函数拟合曲线段，而用线性函数拟合直线段；也就是说，这一问题在数学上即为非线性回归分析的分段拟合问题，且由于分段点未知，求解这一问题就涉及到全局优化(global optimization)问题。因此，本文选用七维高科所开发的数学优化分析软件1stOpt，通过其核心算法——通用全局优化(universal global optimization, UGO)算法来求解双函数段的分段拟合问题的最优解[18]。

由于可用于非线性回归问题的全局优化算法有很多，依据算法优化利用的数据信息可分为两类：一类是利用函数值和导数值信息进行迭代的Levenberg-Marquardt优化法(LM+UGO)、BFGS准牛顿优化法(BFGS+UGO)、共轭梯度优化法(conjugate gradient method, CGM+UGO)；另一类则是直接利用函数值信息进行比较计算的Powell优化法(Powell optimization, PO+UGO)、单纯形优化法(simplex method, SM+UGO)，以及基于进化算法的差分进化法(differential evolution, DE)与最大继承优化法(max implementation optimization, MIO)[18-20]。本文将讨论上述方法在求取张力计反应时间的实用价值与局限性，包括曲线段的最佳拟合函数、计算效率、优化解的合理性与稳定性等，最后依据分析结果，给出了适合求取张力计反应时间的优化方法与建议。此外，为了便于对比各方法的计算结果，优化方法所需的计算参数，除MIO采用种群数40、变异率0.01外，其他参数均采用软件的默认值。

2 结果与讨论

2.1 张力计读数的响应特征

通过土柱试验所测得的张力计压力读数与时间关系可知：张力计插入土体，会使土体受到挤压扰动，导致张力计读数发生剧烈变化，甚至会出现正值的超静孔压或较高值的基质吸力；张力计受到土中基质吸力的作用，会使陶土头内的水与其周围土体的水产生流动，直至土体的基质吸力与张力计传感器受到的压力相互平衡(此过程即为压差反应，其造成张力计可合理测量土的基质吸力的时间相对滞后)。因此，张力计读数随时间的响应特征可分为3段：张力计安装扰动段、压力反应滞后段以及稳定平衡段(图1)。

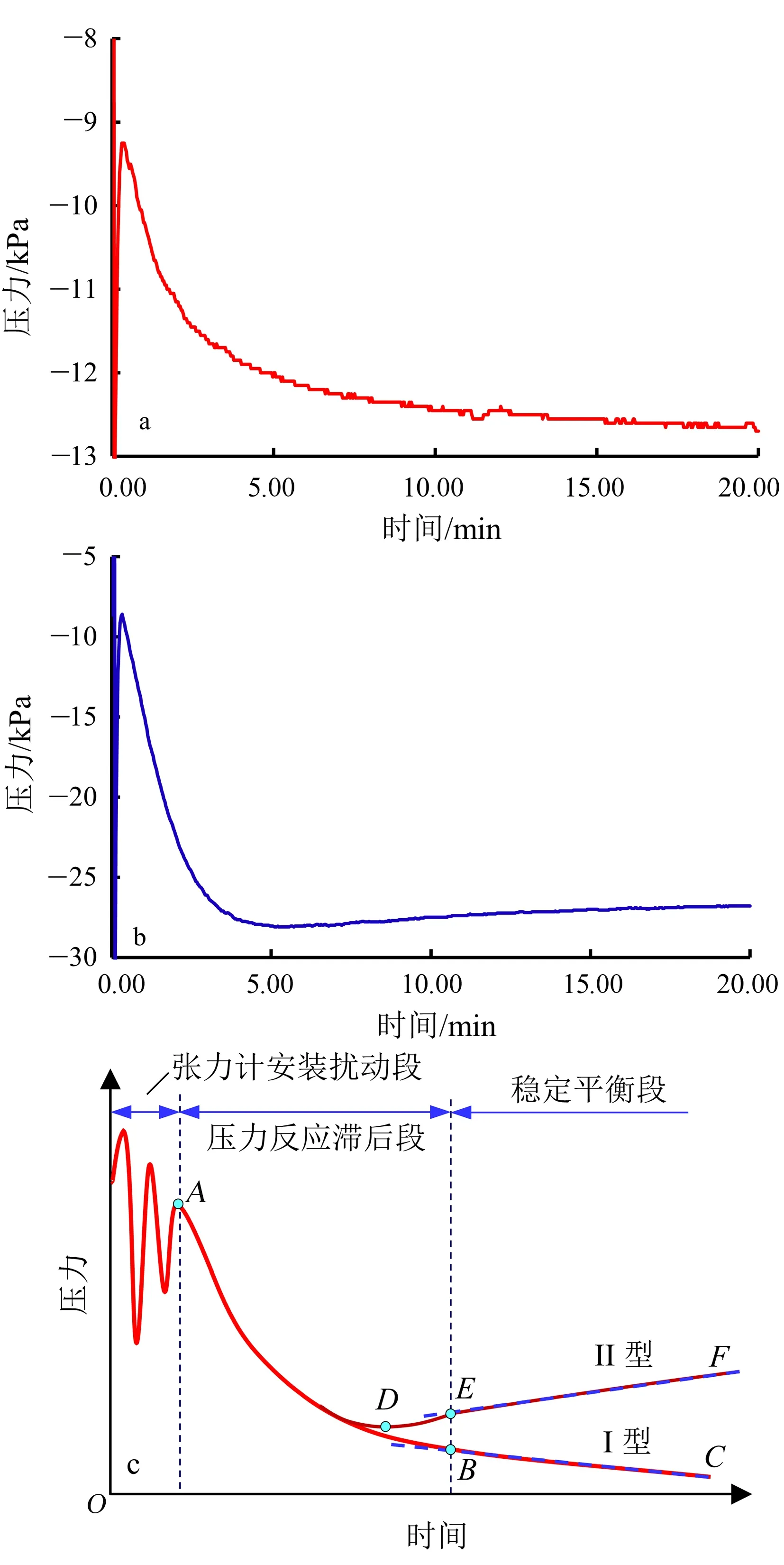
a. 泾阳湿土(Ⅰ型)；b. 定边中湿土(Ⅱ型)；c. Ⅰ型和Ⅱ型响应曲线特征。

试验结果表明，稳定平衡段的压力-时间关系曲线可近似为直线，并可依其斜率分为3种不同的情况：一是所测得的压力随时间缓慢减少(基质吸力缓慢增加，斜率为负)，这可能是土柱环境处于微量蒸发情况(陶土头周围土体水分缓慢减少)所导致；二是测得的压力基本保持不变(斜率较小，接近于0)，亦即陶土头周围土体的水分基本没有变化；三是压力读数随时间缓慢增加(斜率为正)，造成这一现象的原因可能是土体受到张力计陶土头及其有机玻璃管表面附着水的影响，使土的含水量微增，导致所测量的孔压也缓慢增加。

此外，也可依据压力反应滞后段是否产生明显的极值现象将响应曲线分为2种类型：一类是所测得的孔压响应先逐渐减少，再趋于稳定(Ⅰ型，响应曲线可近似为单调递减型，即稳定平衡段的斜率为负或斜率较小接近于0)(图1a、c)；另一类则是孔压先减后增，再趋于稳定(Ⅱ型，存在明显的局部极值点，即稳定平衡段的斜率为正)(图1b、c)。其中，张力计插入土体那一瞬间的时刻设为0点。依据试验结果，泾阳湿土、泾阳中湿土、泾阳干土、定边湿土、定边干土、毛乌素中湿砂与毛乌素干砂的张力计读数响应特征为Ⅰ型；定边中湿土和毛乌素湿砂为Ⅱ型。

试验结果表明，基质吸力较大的情况通常为Ⅰ型，而基质吸力较小的情况则多为Ⅱ型。值得一提的是，定边中湿土的基质吸力较泾阳湿土高，但其压力响应特征为Ⅱ型，这可能是由前述陶土头及其有机玻璃管表面的附着水所导致。

此外，从张力计测量的压力响应特征(图1c)可看出，压力反应滞后段与稳定平衡段具有不同的函数特征，如果我们将压力反应滞后段用非线性函数表示，稳定平衡段用线性函数表示，则可通过非线性分段拟合的数值优化算法来求出张力计的反应时间。可以预见，对于Ⅰ型响应曲线(ABC)，除了数据点出现突然抖动现象(如在数采过程中，误触试验设备)外，数值优化算法一般不会遇到局部最优解问题；但对于Ⅱ型响应曲线(ADEF)，则可能会搜索到局部最优解D点，而非全局最优解E点。

2.2 压力反应滞后段拟合函数的确定

如前所述，张力计的压力响应曲线可分为两种不同的类型，显然地，采用多项式函数可同时满足这两类压力反应滞后段的拟合需求，且高次多项式的R2要高于低次多项式。为了确定用于拟合压力反应滞后段的多项式函数的合适次数，本文将前述的泾阳湿土和定边中湿土作为典型案例，对其开展3～8次多项式反应时间估算的非线性回归分析工作；其中，数值优化法采用BFGS+UGO计算，结果如表2所示。此外，计算结果表明，对于泾阳湿土(Ⅰ)，各多项式拟合的R2为0.996 5～0.998 8，而定边中湿土(Ⅱ)拟合的R2为0.998 2～0.999 3，从R2值来看，各多项式均有较高的拟合度。

表2 典型案例中多项式次数对张力计反应时间估算的回归分析结果与图解法的对比

尽管高次多项式的拟合结果也很好，但不一定可以得出与图解法相近的结果，两者的差异有时非常明显，导致这一结果的原因是采用高次多项式会将部分稳定平衡段一并拟合，使所得的反应时间较图解法大许多。计算结果表明，压力反应滞后段需采用4次多项式拟合才能有效求取张力计的反应时间，而较低次的多项式或较高次的多项式都不适合作为压力反应滞后段的拟合函数。

2.3 数值优化方法的计算效率

由于涉及非线性回归的数值优化算法非常多，要在这些方法中进行优选，除了要考虑计算结果的合理性外，还需考虑计算效率。因此采用同一台电脑针对典型案例开展各算法的计算工作，并统计各算法所需的计算时间，以分析这些方法的计算效率，作为方法比选的依据。各方法的计算时间整理于表3。

由表3可知，两种类型中，除了CGM+UGO与PO+UGO外，其他方法所需的计算时间均较短，而PO+UGO耗时最久，其所需时间甚至是CGM+UGO的1.74倍以上。因此，如果考虑计算效率，不建议采用PO+UGO分析。

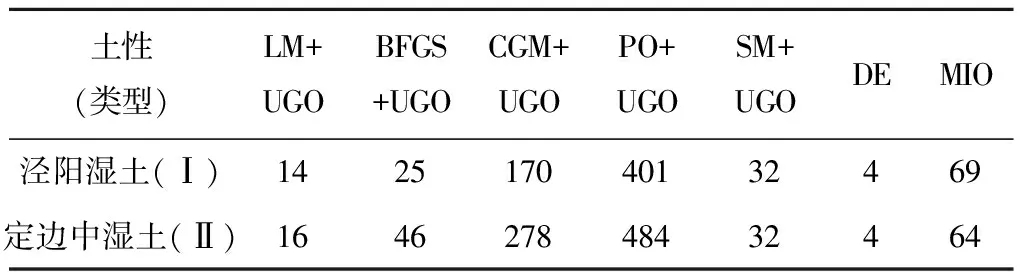
表3 各数值优化方法计算典型案例所需的计算时间

2.4 数值优化解与半经验图解法的对比分析

为了衡量各数值优化方法是否适合求取张力计的反应时间，本文先从典型案例计算，并与图解法的结果(表2)对比，各方法的计算结果整理于表4。对于泾阳湿土(Ⅰ)，各方法拟合的R2为0.998 0～0.998 1，而对定边中湿土(Ⅱ)拟合的R2为0.998 4～0.998 5。

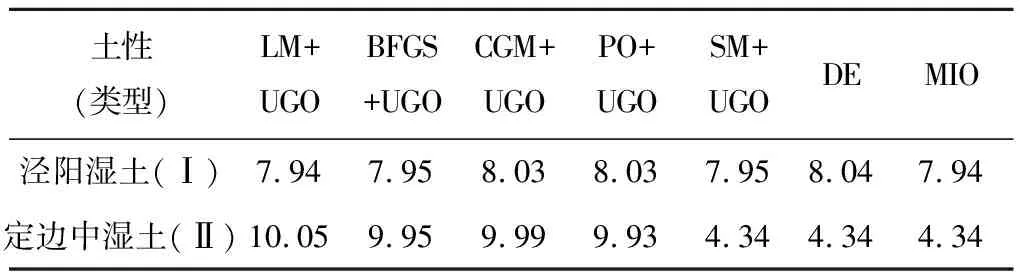
表4 各数值优化方法计算典型案例的反应时间

计算结果表明，对于没有明显局部极值的Ⅰ型响应曲线，各数值优化方法所计算的结果与图解法所得结果差异不大。对于有明显局部极值点的Ⅱ型响应曲线，LM+UGO、BFGS+UGO、CGM+UGO与PO+UGO等法与图解法的结果相近；然而，SM+UGO、DE和MIO等方法却得出局部极值附近的解，而非全局最优解，且这一解的值稍小于试验得出的局部极值(约在5.00 min，图1b)。

导致这一结果的原因可从算法原理来分析。对于SM+UGO，其是通过不断对比、筛选、替换相邻个体直至选出其中的最优解，由于这一过程是对邻近的点作比较，故常收敛到离初始位置较近的局部最优解上，因此对于存在多局部最优解或相邻局部最优解距离较远的问题时，则不易得出全局最优解[19]。而DE和MIO均为演化算法，其是通过对全数据点组成的群体进行变异、杂交和选择操作，并可借此提高计算效率(表3)。但这也会降低原有群体的多样性，不利于求得全局最优解，甚至会导致搜索停滞的问题[20]；这使得这两种方法在处理有局部极值的Ⅱ型张力计响应曲线时，易陷入局部最优解。因此，对于DE和MIO往往需通过测试才能确定出合适的参数设置来避免这一问题，而这无疑会降低这两种方法的实用价值。综合上述分析，不建议采用SM+UGO、DE和MIO等数值优化方法来求取张力计的反应时间。

此外，为了进一步验证LM+UGO、BFGS+ UGO、CGM+UGO与PO+UGO等法的实用性，本文针对其他土性进行验算工作，并与图解法的估算结果相比较，其结果如表5所示。各方法对于泾阳中湿土(Ⅰ)、泾阳干土(Ⅰ)、定边干土(Ⅰ)、毛乌素中湿砂(Ⅰ)、毛乌素干砂(Ⅰ)与毛乌素湿砂(Ⅱ)的R2依次为0.996 2、0.999 2、0.999 2、0.994 4、0.994 3与0.940 2；而定边湿土(Ⅰ)的R2在0.982 1～0.982 2之间。从R2值来看，毛乌素湿砂(Ⅱ)的拟合效果稍不如其他土性，这是由于在湿砂中张力计读数的抖动较其他土性明显偏多(图2)。导致这一现象的原因主要有二，一是安装在砂土的张力计容易受到外力而晃动，二是砂土的基质吸力较小，读数抖动的幅值对拟合效果的影响较大。

由表5可知，对于除典型案例以外的7种土，数值优化方法所计算的结果与图解法差异同样不大，即使对于R2值相对较小的毛乌素湿砂(Ⅱ)，其计算结果仍在可接受的范围。以图2所示的毛乌素湿砂的张力计实测读数与BFGS+UGO的计算结果来说明，由于所记录的压力读数呈现一定的数据抖动现象，使得半经验图解法不易较快且合理地求得张力计的反应时间；但如能辅以数值优化法所预测的稳定平衡段的拟合直线，则有助于张力计反应时间的合理确定，并可缩短张力计反应时间判定所需的时间。此外，可以预见，倘若数据抖动出现在张力计反应时间点附近或存在突变型张力计响应曲线特征，数值优化方法将不易得出较为合宜的张力计反应时间。

数值优化计算结果表明：对于张力计响应曲线较为平滑的情况，LM+UGO、BFGS+UGO、CGM+UGO、PO+UGO等数值优化方法可用来确定张力计的反应时间；但对于数据抖动幅度较大或存在突变型曲线特征的情况下，仍需借由经验判断才能确定合宜的反应时间。

2.5 数值优化解的稳定性分析

需说明的是，由于数值优化法所得的解并非唯一解，因此本文针对前述的典型案例，将LM+UGO、BFGS+UGO、CGM+UGO、PO+UGO等方法重复计算10次，探讨所得解的稳定性，计算结果如表6所示。

数值稳定性分析结果表明：PO+UGO在计算Ⅱ型的定边中湿土，10次中就有1次陷入局部最优解，而得不到全局最优解；而LM+UGO、BFGS+UGO、CGM+UGO等法尽管每次计算都有些微差异，但整体来看，这3种方法均能合理估算张力计的反应时间，其中又以BFGS+UGO的标准差与变异系数最小。

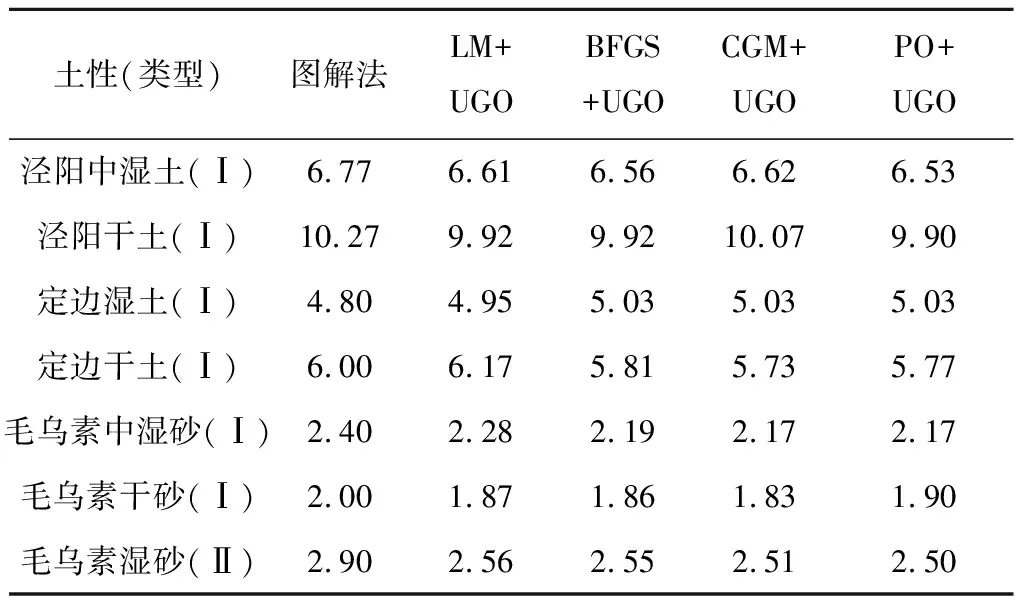
表5 各数值优化方法计算的反应时间与图解法的比较

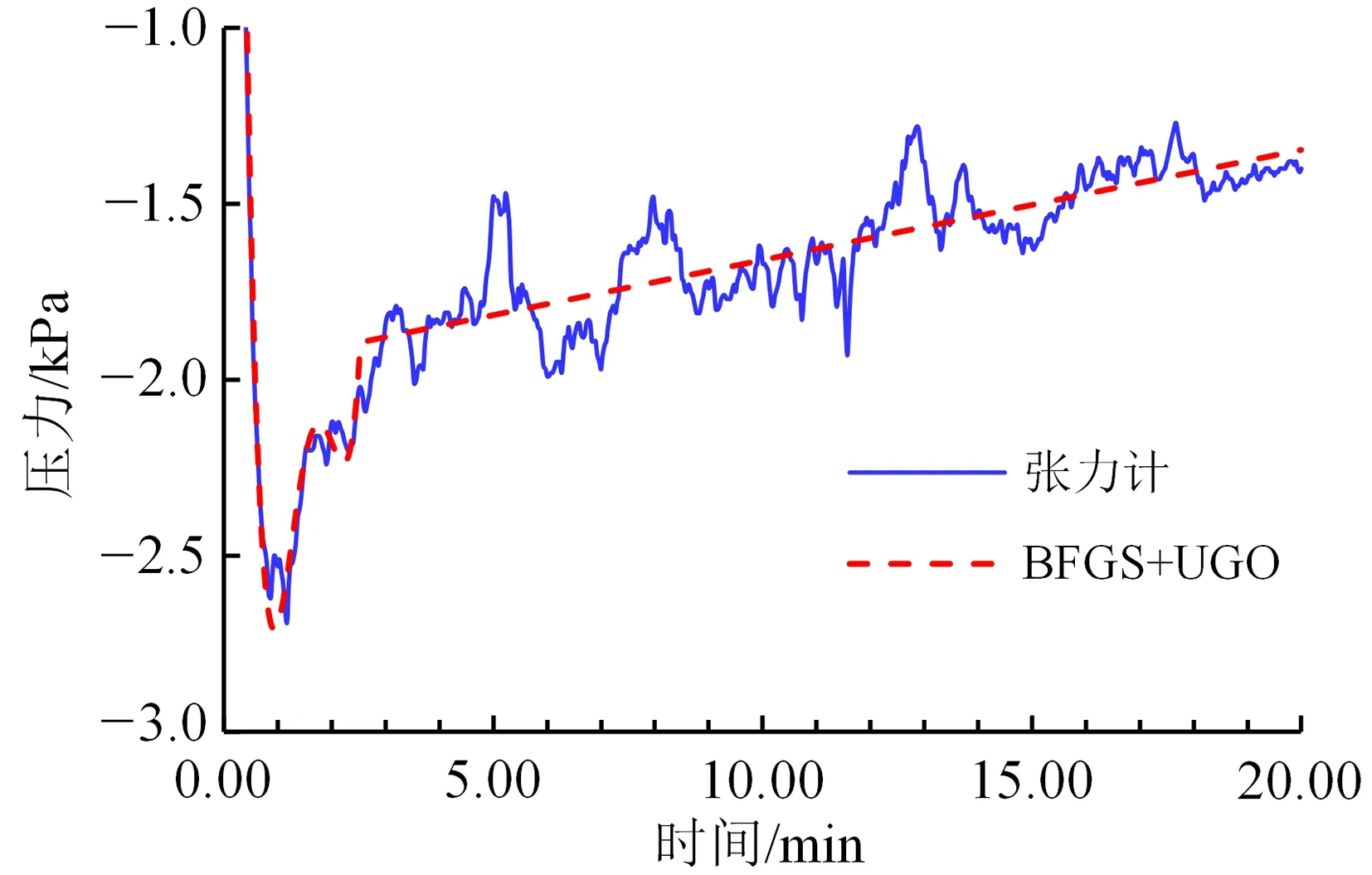
图2 毛乌素湿砂的张力计压力响应曲线与BFGS+UGO的预测结果的对比

同样地，也可从PO的算法原理来分析PO+ UGO陷入局部最优解的原因。PO在本质上也是一种共轭梯度法，但与CGM不同的是，其是通过直线搜索技术寻找一组共轭方向，因此仅需计算目标函数值而不必求出导数值。由于PO+UGO的搜索起点系由1stOpt软件随机给出，这使得仅利用函数值信息的优化算法易因某一搜索起点不当，而在某一循环方向组中的矢量系出现线性相关的情况，导致所得出的解是局部最优解而非全局最优解，甚至会造成无法收敛的结果[18]，这也是造成PO+UGO计算时间偏长的原因(表3)。因此，尽管本文所计算的案例中，10次仅有1次得出局部最优解，仍不建议采用PO+UGO来确定张力计的反应时间。

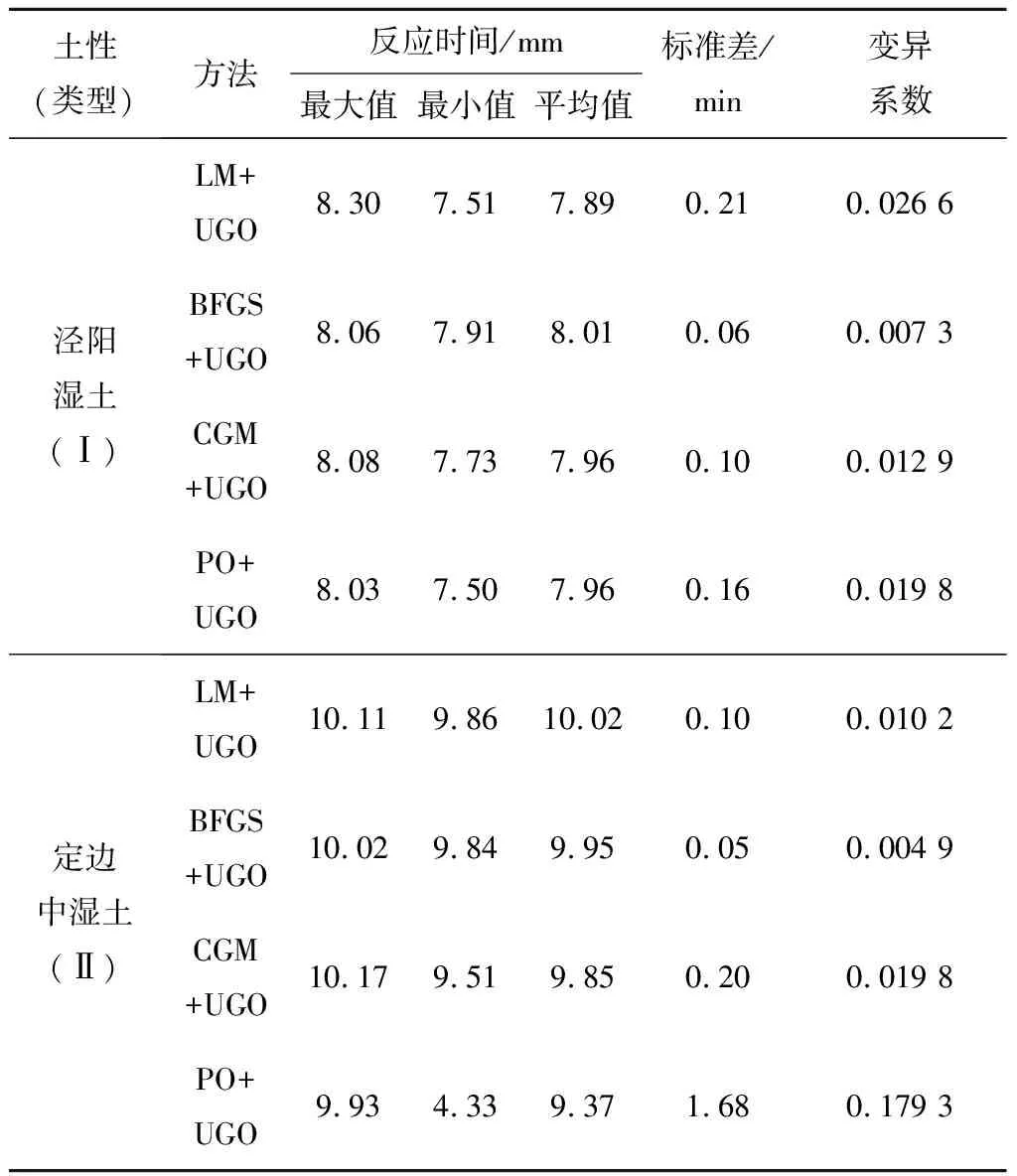
表6 各数值优化方法计算典型案例解的稳定性分析结果

3 方法建议与操作流程

综上所述，利用数值优化算法确定张力计反应时间的方法与流程可总结如图3所示，其步骤简述如下：

1)利用标准化的土柱试验型式(控制土体的均匀性、密封性，并静置使土中水的分布再平衡)，测定张力计响应曲线，并剔除张力计安装扰动段的数据点，得出张力计压力反应滞后段与稳定平衡段的响应曲线(图1c)。

2)采用全局优化算法的数值优化法求解非线性回归分析的分段拟合问题。其中，数值优化算法建议选用LM+UGO、BFGS+UGO或CGM+UGO。

3)张力计响应曲线的压力滞后段建议采用4次多项式函数拟合，而稳定平衡段则用线性函数拟合。

4)审视数值优化方法所得的双函数段分段点所对应的时间是否为合宜的张力计反应时间。

5)若数值优化方法得出合理的张力计反应时间，则建议计算5～10次，再求取其平均值，以作为张力计的反应时间；若所得结果陷入局部最优解或因数据大幅抖动导致计算结果不理想，再通过经验判断修正。

通过上述步骤可求得较为标准化的张力计反应时间，以减少过多的人为干预和误差等问题，并缩短判定所需的时间。所得的张力计反应时间，可用以估算非饱和土的渗透系数或应用于不同张力计型式的比选上(如：可通过上述方法，求得不同型式张力计的反应时间，对于基质吸力变化速率较快的环境，需选用反应时间短的张力计)。此外，也可借由本文所介绍的张力计反应时间的确定方法，来评估所研制的新型张力计的实用价值。

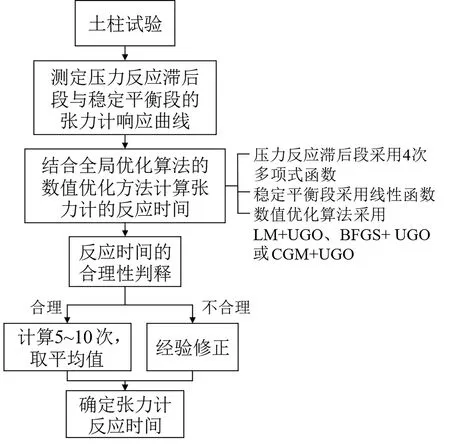
图3 张力计反应时间测定流程图

4 结论

1)土柱试验结果表明，张力计的响应曲线可分为张力计安装扰动段、压力反应滞后段以及稳定平衡段。并可依其在压力反应滞后段内是否出现明显的极值现象，区分为两种类型：一类是所测得的孔压响应先逐渐减少，再趋于稳定(Ⅰ型，响应曲线可近似为单调递减型)；另一类则是孔压先减后增，再趋于稳定(Ⅱ型，存在明显的局部极值点)。

2)从张力计的响应曲线来看，压力反应滞后段与稳定平衡段具有不同的函数特征，两者的分界点即为反应时间，因此可用非线性回归分析的数值优化方法结合全局优化算法求取张力计的反应时间。研究结果表明，压力反应滞后段可采用4次多项式函数拟合，而稳定平衡段则用线性函数拟合。

3)对于没有明显局部极值的Ⅰ型响应曲线，各数值优化方法所计算的结果与图解法所得结果差异不大；但对于有明显局部极值点的Ⅱ型响应曲线，PO+UGO、SM+UGO、DE和MIO等方法会陷入局部最优解的问题。

4)在一般情况下，LM+UGO、BFGS+UGO、CGM+UGO等方法可合理估算张力计的反应时间。但对于数据抖动幅度较大或存在突变型曲线特征等复杂形式的张力计响应曲线，数值优化算法仍不易获得较理想的结果，此时需借由经验判断，以合理确定张力计的反应时间。