数轴——确定字母范围的神器

文／余丹丹

一元一次不等式（组）中含字母范围的问题，代数特征明显，比较抽象。在做题时，我们如何化抽象为形象呢？数轴是确定字母范围的神器，能帮助我们拨开字母范围的迷雾。

例1若不等式组无解，则m的取值范围是________。

【解析】解不等式组的本质，就是找几个不等式的解集的公共部分。运用数形结合思想，我们可以将问题转化为图形问题。

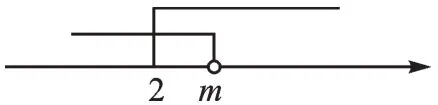
图1

图2

例2若不等式x＜m的正整数解有2个，求m的取值范围。

【解析】由不等式x＜m的正整数解有2个，不难知道，这两个正整数解只能是1、2。因此，如图3，数轴上m点只能在2的右侧和3的左侧，而且不能与2重合，但可以与3重合。所以m的取值范围为2＜m≤3。本题要注意，我们不仅要考虑2在解集里，而且要考虑3不在解集里。

图3

例3关于x的不等式-2k-x+6＞0 的正整数解只有1、2、3、4，求k的取值范围。

【解析】我们先确定不等式的解集为x＜-2k+6，然后根据正整数解只有1、2、3、4，把“-2k+6”当成一个整体，利用数轴来确定“-2k+6”的范围。由图4可知，-2k+6必须要大于4且小于或等于5，解得≤k＜1。

图4

例4 若不等式a≤x≤a+1 中每一个x的值都不满足不等式1＜x＜3，则a的取值范围是_________。

【解析】先在数轴上表示出1＜x＜3 和a≤x≤a+1，如图5。1＜x＜3 的区域是固定的，而a≤x≤a+1 的区域是可以移动的。a≤x≤a+1 中每一个x的值，都不满足1＜x＜3，也就是说，1＜x＜3与a≤x≤a+1没有公共部分。所以，我们移动a≤x≤a+1 的区域，如图6，发现当a+1≤1或a≥3时满足题意，进而可得a≥3或a≤0。

图5

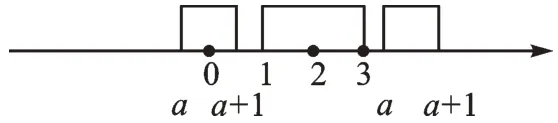
图6