区域地表水主要污染物的主成分分析

2022-06-23金志浩王晨君魏亚龙

绿色科技 2022年10期

金志浩，王晨君，魏亚龙

(上海市虹口区环境监测站，上海 200083)

1 引言

在水质污染状况分析时，需考虑影响水质状况的多种因素。为减少分析问题的复杂性，学者们致力于从众多的影响因素中剔除含重复信息或测量误差太大的因素，找到最佳的关键因素组合[1～4]。主成分分析作为一种定量化研究的多元统计分析方法，可以利用降维思路，在数据损失最少的原则下，把多指标转化为少数几个综合指标，能够客观地确定影响水质的主控因子，相较于其他方法有一定的优越性，并在解决实际问题中取得了良好的成效，是环境质量综合评价一种简单有效的方法[5～8]。本文采用SPSS软件对某区域地表水主要污染物进行主成分分析，从而探究该分析方法在水质污染状况评价中的可行性[9～15]。

2 研究方法

数据来源于2019年上海市虹口区生态环境局发布的生态环境质量报告书[16]，包括区域内11个地表水监测断面的溶解氧、高锰酸盐指数、化学需氧量、五日生化需氧量、氨氮、总磷、总氮、挥发酚和石油类等9种主要水质污染物监测指标的年均值。

主成分分析法，采用SPSS22.0统计软件，进行单因素方差分析，比较差异的显著性，并确定水体主要污染因子，从而探讨影响水质状况的主要因素。

综合水质指数法，采用单因子评价法，根据GB 3838-2002《地表水环境质量标准》对地表水监测断面的各监测指标进行评价。

3 结果与讨论

3.1 数据标准化处理

2019年虹口区11个地表水监测断面的水质监测结果(年均值)，如表1所示。

将表1中所列的数据进行标准化处理，构成标准化矩阵Z，其Z元素分布表(无纲量)，如表2所示。

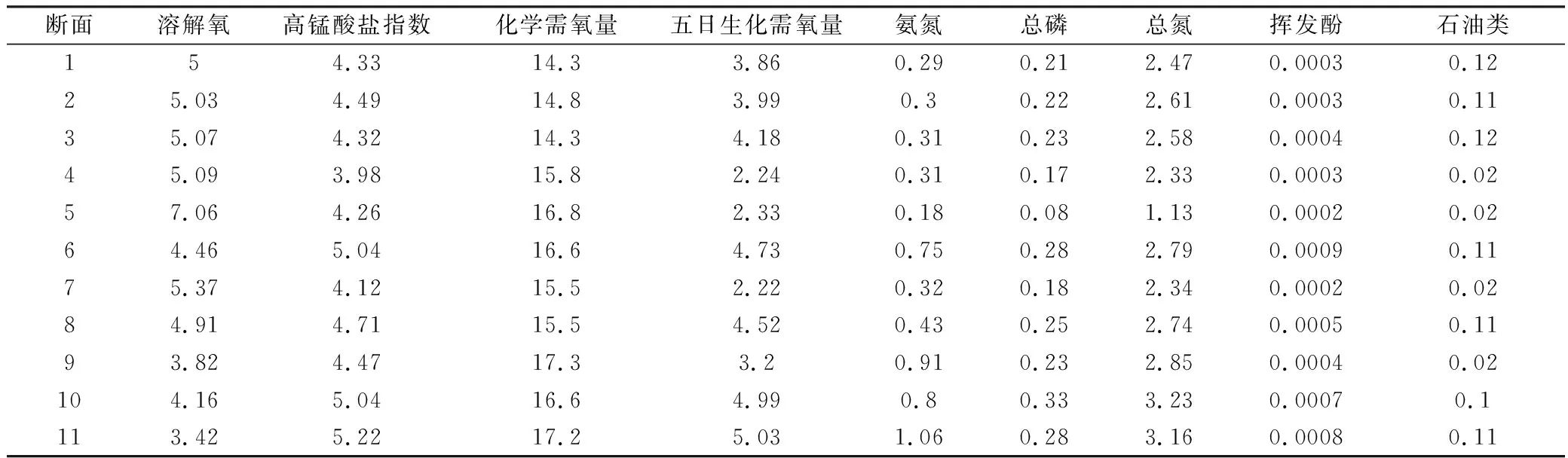
表1 地表水监测结果 mg/L

3.2 主成分分析

对矩阵Z进行主成分分析，求出Z的协方差矩阵的特征值，计算结果如表3所示。

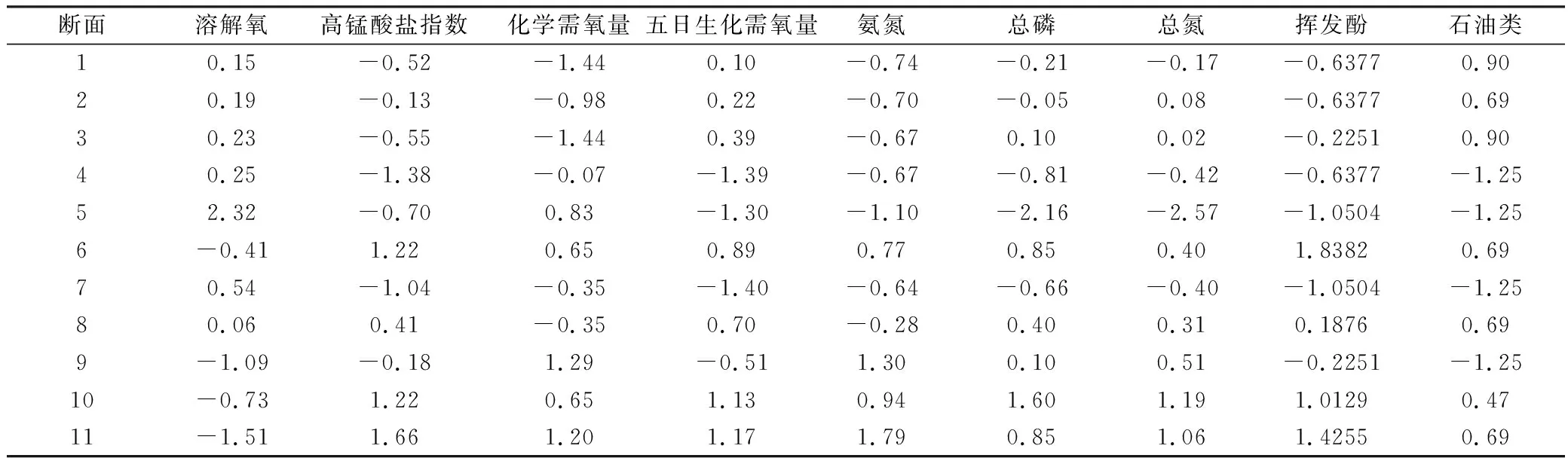
表2 标准化矩阵Z元素分布

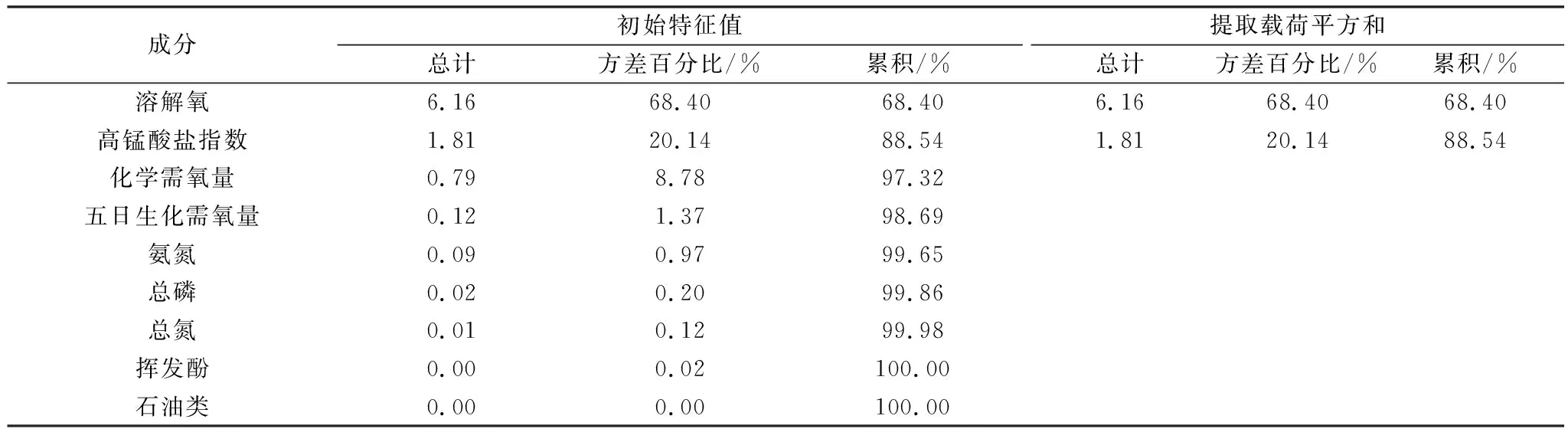
表3 主成分特征值和累计贡献率

由表3可知，特征值λ1=6.16，λ2=1.81，第1、2主成分占总方差的相对贡献为88.54%[17]。一般认为累计方差贡献率大于85% 时，就能保证不丢失太多的重要信息[18]。因此，可以把第1、2主成分作为共同因子。9个参数在第1、2公共因子上的主成分矩阵，如表4所示。

表4 主成分矩阵

由表4可知：主成分与指数变量之间有着相关关系。第1成分与溶解氧之间有着较强的负相关关系，与其他因子之间有较强的正相关关系。第2成分与溶解氧、五日生化需氧量、总磷、总氮、石油类之间有着一定的负相关关系。可以看出，第1、2主成分均与溶解氧指标有着较强的相关关系，这可能是由于溶解氧是首要污染因素所导致的。