基于随机抽样的近似聚集查询处理综述

胡 欢，李建中

（哈尔滨工业大学 计算机科学与技术学院，哈尔滨 150001）

0 引言

近似查询处理（approximate query processing，AQP）是数据库领域中一个重要的研究方向，而近似聚集查询是AQP 的核心研究问题。常用的处理近似聚集查询的方法包括随机抽样、直方图、小波变换、草图等等。在这些方法中，只有随机抽样能够应对较复杂的聚集查询（比如包含复杂的选择条件、连接操作等等）。因此，本文将研究基于随机抽样的近似聚集查询。文献［1，3，5，6］总结了大量相关工作。随机抽样大体可分为在线随机抽样和离线随机抽样两种方式。接下来，先分别概述基于在线随机抽样和基于离线随机抽样的近似聚集查询的研究现状，然后简要探讨近似聚集结果的误差估计的主要方法。

1 聚集查询

简单来说，聚集查询是返回一个或多个聚集值的SQL 查询的统称。聚集值可以是均值（AVG）、求和（SUM）、方差（VAR）、标准差（STDEV）、计数（COUNT）、最大值（MAX）、最小值（MIN）等等。文献中提出的各种方法通常只适用于特定的一类聚集查询。假设＄T ＄是一张有d＋d个属性的表，D＝｛，，…，D｝ 为上的选择属性集合，D＝｛，，…，M｝为上的聚集属性集合。那么，一个基本的聚集查询如下所示：

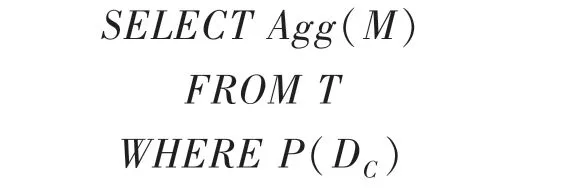
其中，（D）是D上的一个谓词，作为对表的选择条件，（）是∈D上的一个聚集操作。该聚集查询的语义是在＄T ＄的满足选择条件（D）的所有行上执行聚集操作（）。通常，一个更复杂的聚集查询可以在上述基本聚集查询的基础上进行如下扩展：

（1）增加分组操作（GROUP BY），对分组后的数据分别计算聚集值。

（2）增加连接操作（JOIN），对多个表连接后的结果计算聚集值。

（3）聚集操作，作用在不同列之间的计算结果之上，比如（），其中，∈D。

聚集查询处理作为联机分析处理（online analytical processing，OLAP）的一个基本组成部分，被广泛运用于决策支持系统，以帮助企业进行商业决策。

2 基于在线随机抽样的近似聚集查询研究

基于在线随机抽样的近似聚集查询会在每个聚集查询到来的时候进行抽样，并且使用抽到的样本集来处理当前查询。其优点是可以根据不同查询的特点有针对性地抽样，比如使用索引结构在满足选择条件的数据上进行抽样，也可以自由控制样本集的大小以保证聚集结果足够准确。但其缺点也很明显，需要为每个查询重新进行一次随机抽样，开销比较大。下面拟对主要相关工作进行简要回顾与论述。

在上世纪80 年代，Olken 等人就已经开始研究基于在线随机抽样的近似聚集查询了。到了上世纪90 年代末，Hellerstein 等人提出了众所周知的在线聚集，是以交互的方式处理聚集查询。举例来说，一个支持在线聚集的系统会在一个聚集查询被提交后不断进行抽样、更新近似聚集结果并将其连同误差一起反馈给用户。一旦用户对当前近似聚集结果满意，就可以手动提前终止该查询，从而节省时间。在线聚集一经提出就引起了学术界的广泛关注。此后出现了大量在线聚集相关的工作。比如，Qin 等人提出了第一个并行计算环境下的在线聚集框架PF-OLA。PF-OLA 将计算近似聚集结果和估计误差两项任务并行，以提高查询的响应速度。Zhang 等人利用多核CPU 与多核GPU 的并行计算能力加快在线聚集的处理。此外，Condie 等人修改了Hadoop 上的MapReduce 框架以支持分布式在线聚集，而Pansare 等人提出了一个适合于MapReduce 框架的在线聚集模型并且在一个开源项目Hyracks 上实现了该模型。Zeng 等人提出了一个在线聚集模型G-OLA，以有效处理任意嵌套的聚集查询。

当聚集查询涉及多个表之间的连接时，在线聚集变得复杂多了。Haas 等人提出的Ripple Join方法简单地先从要做连接的每个表中随机抽取一个样本集，然后在这些样本集上进行连接。这种盲目的抽样方法很容易使得某些聚集结果缺失或者聚集结果误差很大。Acharya 等 人提出的 Join Synopses 方法只在第一个表上抽取一个样本集，然后将之与其他表进行连接。当其他表很大时，这种方法效率会很低。稍后，Li 等人提出的Wander Join 方法以随机游走的方式有选择性地抽样，能够取得较高的效率。但是，这种方法需要大量索引结构，因此预处理开销和存储开销大。Zhao 等人指出通过Ripple Join 方法得到的一个多表连接结果的样本集是均匀、但非独立的，而通过Wander Join 方法得到的一个多表连接结果的样本集是独立、但非均匀的，进而又提出了一个生成均匀独立样本集的框架。

3 基于离线随机抽样的近似聚集查询研究

基于离线随机抽样的近似聚集查询会在预处理阶段从原始数据上抽取一个随机样本集并保存起来以用于处理之后到来的多个查询。可见，相较于基于在线随机抽样的近似聚集查询，基于离线随机抽样的近似聚集查询不需要为每个查询进行一次抽样，因此具有响应速度快的特点。不过，后者由于使用同一个样本集来处理多个不同的查询，可能导致这些查询的近似聚集结果之间具有相关性，从而出现误差传播问题。下面将对主要相关工作做简要回顾与论述。

基于离线随机抽样的近似聚集查询通常假设聚集查询任务是相对固定的（试想一下，如果聚集查询任务不固定，那么几乎需要把整个数据集当作样本集才能保证任意查询的聚集结果误差足够小）。这样一来，研究的基本思想是根据给定的聚集查询任务有针对性地使用各种非均匀抽样方法进行抽样，使得得到的样本集尽可能小，而且在此之上估计出来的近似聚集结果误差尽可能小。在现有相关文献中，比较受欢迎的处理方法是基于查询列集（query column set，QCS）的方法。这种方法在具有相同QCS 的聚集查询之间共享一个样本集。这个样本集可能不大，却能够保证查询结果的准确度足够高。然而，这种方法的不足也是显而易见的：QCS 的个数可能很大，因此为每个QCS 抽一个样本集可能需要大量预处理时间，而且存储这些样本集也可能需要大量空间开销。

最近，有不少工作通过结合离线抽样和其他技术进一步提高了近似聚集查询处理的性能。Galakatos 等人通过在交互式分析中结合离线样本集和先前计算出的近似聚集结果来加速当前聚集查询的计算，从而节省查询处理时间。Peng 等人通过结合离线样本集和精确的预聚集结果来提高查询响应速度和聚集结果准确度。Ding 等人不仅离线地抽取一个样本集用于处理查询，而且在离线样本集不足以保证给定的聚集结果准确度时会临时再通过在线抽样得到更多的样本。

4 误差估计方法

在基于随机抽样的近似聚集查询研究中，近似聚集值的误差通常用一个置信区间来表示。文献［25］强调了准确估计误差的重要性并探讨了大量误差估计方法的优缺点。最主要的3 种误差估计方法分别是基于中心极限定理的方法、基于大偏差界（large deviation bounds）的方法和拔靴法（bootstrap）。对此将给出研究分述如下。

基于中心极限定理的方法不适用于聚集值MIN、MAX 和由用户自定义聚集函数计算出的结果的误差估计。由于中心极限定理依赖于数据总体方差而通常数据总体方差未知，该方法需要假设样本方差等于数据总体方差，进而用样本方差代替数据总体方差。因此，当数据倾斜度很大时该方法不能够准确估计误差。此外，该方法要求数据服从正态分布，除非抽取的样本量“足够”大。

基于大偏差界的方法是一大类误差估计方法，最常用的2 种分别是基于切比雪夫不等式的方法和基于霍夫丁不等式的方法。与基于中心极限定理的方法一样，这类方法也不适用于聚集值MIN、MAX 和由用户自定义聚集函数计算出的结果的误差估计。基于切比雪夫不等式的方法需要做出跟基于中心极限定理的方法相同的假设，而基于霍夫丁不等式的方法不需要做出任何假设。相比于基于中心极限定理的方法和基于切比雪夫不等式的方法，基于霍夫丁不等式的方法的缺点是对离群点很敏感。如果离群点偏离很大，那么该方法会表现得很差。

拔靴法通过不断地重采样来估计聚集值的分布情况进而估计出近似聚集值的误差。该方法的优点是能够适用于比上述2 种方法更多种类的聚集值的误差估计，比如中位数。但是，方法的缺点有2 个。第一是需要不断重采样，时间开销大；第二是依赖于很强的假设，导致估计出来的误差经常不准确。

5 结束语

近二十年来，基于随机抽样的近似聚集查询一直都是学术界的研究热点。在线随机抽样和离线随机抽样这2 种抽样方式在处理近似聚集查询时各有优缺点。样本集大小和聚集结果准确度是评价一个抽样方法好坏的关键指标。现有工作中不同的抽样方法可能基于不同的假设、采用不同的技术、能有效处理不同类型的聚集查询。

当前研究面临若干重大挑战，其中包括没有统一的AQP 模型、没有可靠的查询优化策略、在倾斜数据上难以保证给定的误差界等等。目前，虽然已经开发了一些原型系统，如BlinkDB、SnappyData、Quickr、VerdictDB，但是距离开发出真正成熟的系统却仍有待更进一步的探索和研究。