海翼水下滑翔机测流应用

褚福硕 , 司宗尚 , 庞重光 , 俞建成

(1. 中国科学院海洋研究所海洋环流与波动重点实验室, 山东 青岛 266071; 2. 中国科学院大学, 北京100049; 3. 青岛海洋科学与技术试点国家实验室海洋动力过程与气候功能实验室, 山东 青岛266237; 4. 中国科学院海洋大科学研究中心, 山东 青岛 266071; 5. 中国科学院沈阳自动化研究所, 辽宁 沈阳 110016)

水下滑翔机是一种新型自主水下航行观测平台,其通过改变浮力及俯仰角可以在海洋中实现垂直及水平运动[1], 一般水下滑翔机完成1次1 000 m浮潜测量需要4~6 h。相比锚定和走航式海洋观测平台,水下滑翔机可以实现高精度海洋观测并通过全球卫星定位系统(GPS)实时传输观测数据。除提供如温度和盐度等基本海洋水文要素外, 利用水下滑翔机还可以测量剖面的深度平均流[2-3]。

利用航位推算技术, Davis等[4-5]计算Seaglider水下滑翔机相对于陆地完成1次下潜获得的理论出水速度与利用GPS获得的实际速度之差从而获得深度平均流, 并通过均方根进行误差分析, 其结果显示深度平均流精度为0.01 m/s; Todd等[6]利用船载声学多普勒剖面仪 (ADCP)与Slocum水下滑翔机测量3年加利福尼亚沿岸流对比分析指出其深度平均流不确定性仍为0.01m/s; Rudnick等[7]指出受海洋生物影响, 长期Spray水下滑翔机观测误差随时间逐渐增大, 导致深度平均流均方根误差从0.014 m/s增大到0.017 m/s, 因此在每次使用前需对测量仪器精度漂移误差进行实验室测量校准。

深度平均流是水下滑翔机作为海洋观测平台的独特观测要素。通过实时计算深度平均流, 水下滑翔机可以穿越或跟随复杂的海洋水流环境从而更高效的进行观测。除此之外, 通过积分水下滑翔机连续观测剖面可以获得水体通量, 该通量评估的准确性依赖深度平均流的精度, 如0.01 m/s 的流速误差在水平100 km和水深1 000 m尺度上会产生1 Sv输送误差, 因此利用深度平均流作为参考可以计算包含正压输送的绝对地转流, 从而使得水下滑翔机在边界流观测上具有重要的应用价值[8]。

自2003年起, 中国科学院沈阳自动化研究所及天津大学分别开展了水下滑翔机基础研究工作, 并成功利用研发出的多种型号海翼水下滑翔机和海燕水下滑翔机取得一系列研究成果, 如Huang等[9]提出一种迭代算法优化水下滑翔机路径追踪技术; Ma等[10]利用水下滑翔机理论下水模型成功反演出南海内孤立波[10]; 针对海洋流场, Ma等[11]通过水下滑翔机搭载ADCP和校准水下滑翔机模型参数发现利用ADCP测量海水经向和纬向流速误差均少于0.06 m/s等。

近几年, 中国科学院沈阳自动化研究所研发的海翼水下滑翔机在南海开展了一系列海上观测项目[12], 基于获得温度、盐度, 经纬度, 航向角及俯仰角数据, 我们评估了利用海翼水下滑翔机获得的深度平均流数据以及地转流数据, 并利用船载ADCP校正技术对深度平均流误差做出分析, 同时利用深度平均流计算水下滑翔机穿越西沙群岛冷涡时的绝对地转流。

1 方法

1.1 深度平均流

深度平均流的计算是基于理论出水速度与实际出水速度之差获得[7], 假定水下滑翔机下潜角为φ(相对于水平面), 垂直位移dz, 水下滑翔机航向角θ,滑翔时间为t, 则其理论出水速度为:

1.2 绝对地转流

根据(5)、(6)可以计算绝对地转流, 首先在深度上积分热成风公式[8,13]:

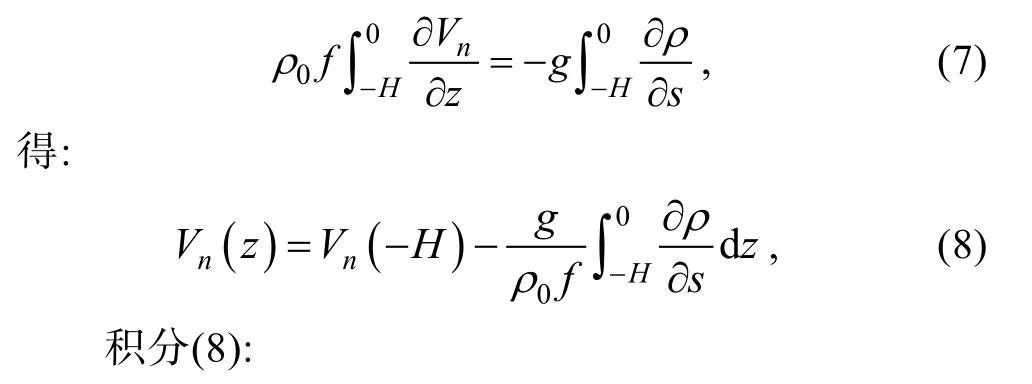
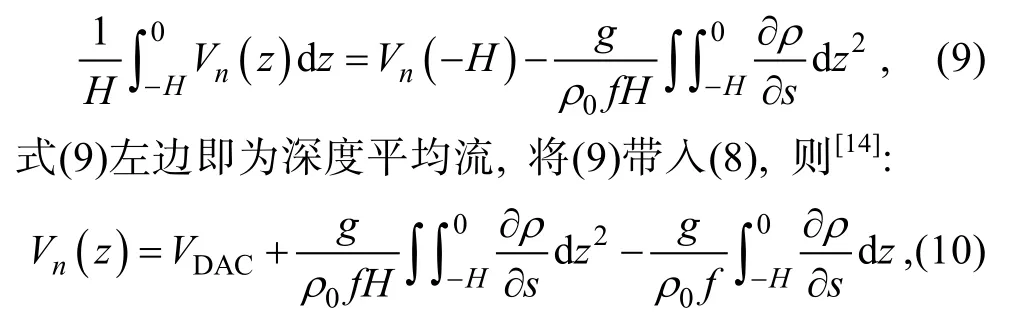
其中,Vn为跨轨迹速度,H为水下滑翔机下潜最大深度,0ρ为参考密度,f为科氏力参数,g为重力加速度,VDAC为深度平均流, (10)式左边第一项为绝对地转流,右边第一和第二项为地转流正压项, 第三项为地转流斜压项[13]。

2 结果分析

2.1 深度平均流

中国科学院沈阳自动化研究所于2018—2019在南海西沙群岛附近开展了一系列水下滑翔机观测计划, 我们选取其中一组数据评估深度平均流, 该水下滑翔机自2018年9月3日至2019年3月31日沿既定轨迹(110.22°E, 17.15°N~111.25°E, 15.18°N)连续重复观测(图1), 最大下潜深度1 012 m, 本次航行共获得933组观测数据, 包括温度、盐度、深度、航向角及经纬度数据。水下滑翔机在海表面通过卫星传输数据, 下潜时通过改变排水体积的方法改变浮力, 其利用回油路上电磁阀带动液压泵反向旋转减小载体外皮囊充油量, 从而减小排水体积完成下潜, 上浮时通过直流电机带动液压泵增大外皮囊充油量, 从而增大排水体积完成上浮。滑翔机在水下保持22°倾角航行,下潜(上浮)时受密度影响其净浮力通量随深度逐渐增大(减小), 因此其下潜(上浮)速度逐渐减小(增大), 其中速度扰动受海洋高频信号如内波影响, 但由于水下滑翔机在水中的下潜深度及倾角保持相对恒定, 水面的深度与水平距离曲线不受内波的影响, 因此其通过水面的水平速度约为0.23 m/s (图2)。

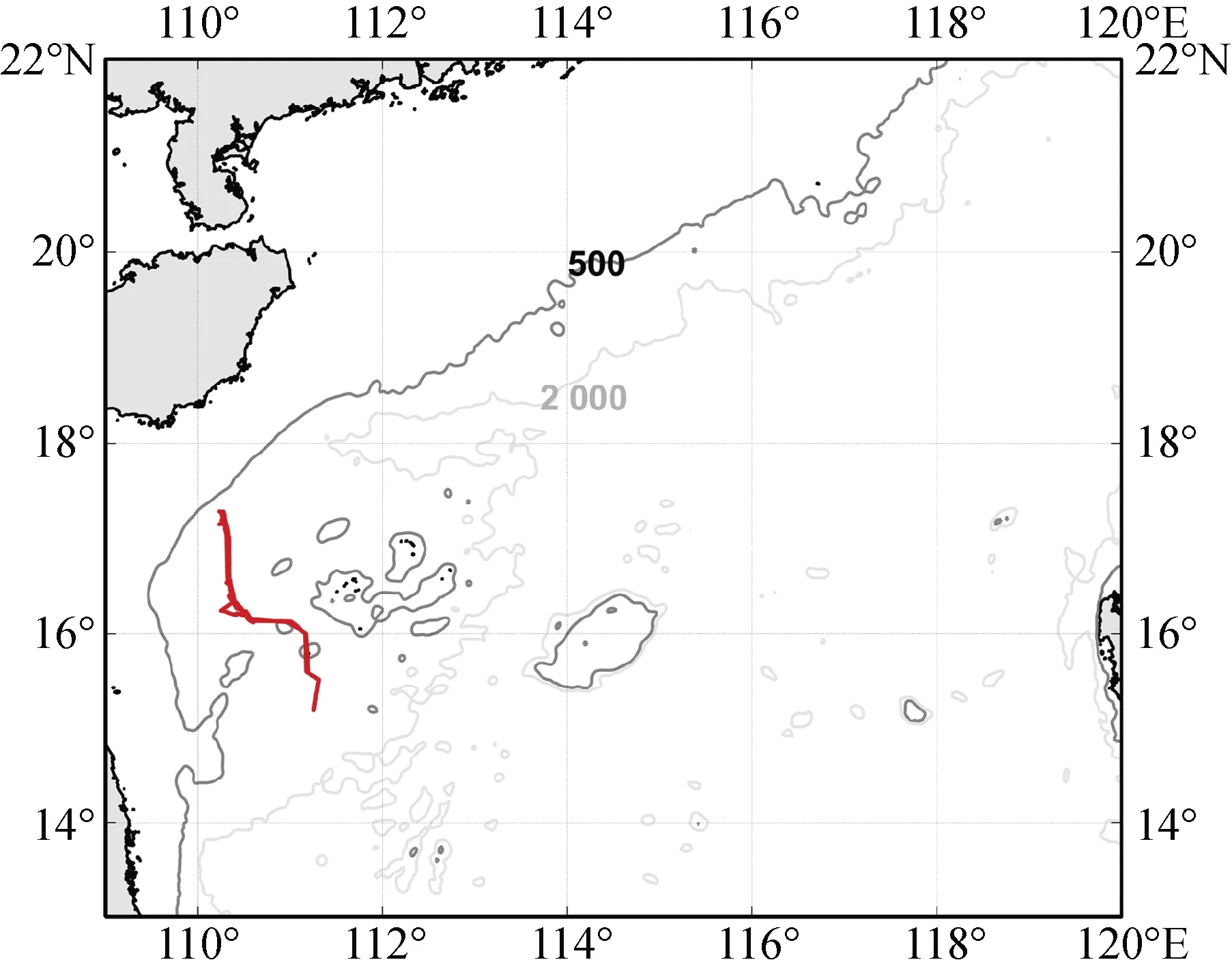
图1 2018年9月—2019年4月海翼水下滑翔机航行轨迹(红线), 等值线代表500 m及2 000 m等深线Fig. 1 Sea Wing glider tracking (red line) from September 2018 to April 2019, Isolines represent 500 m and 2 000 m Isobaths

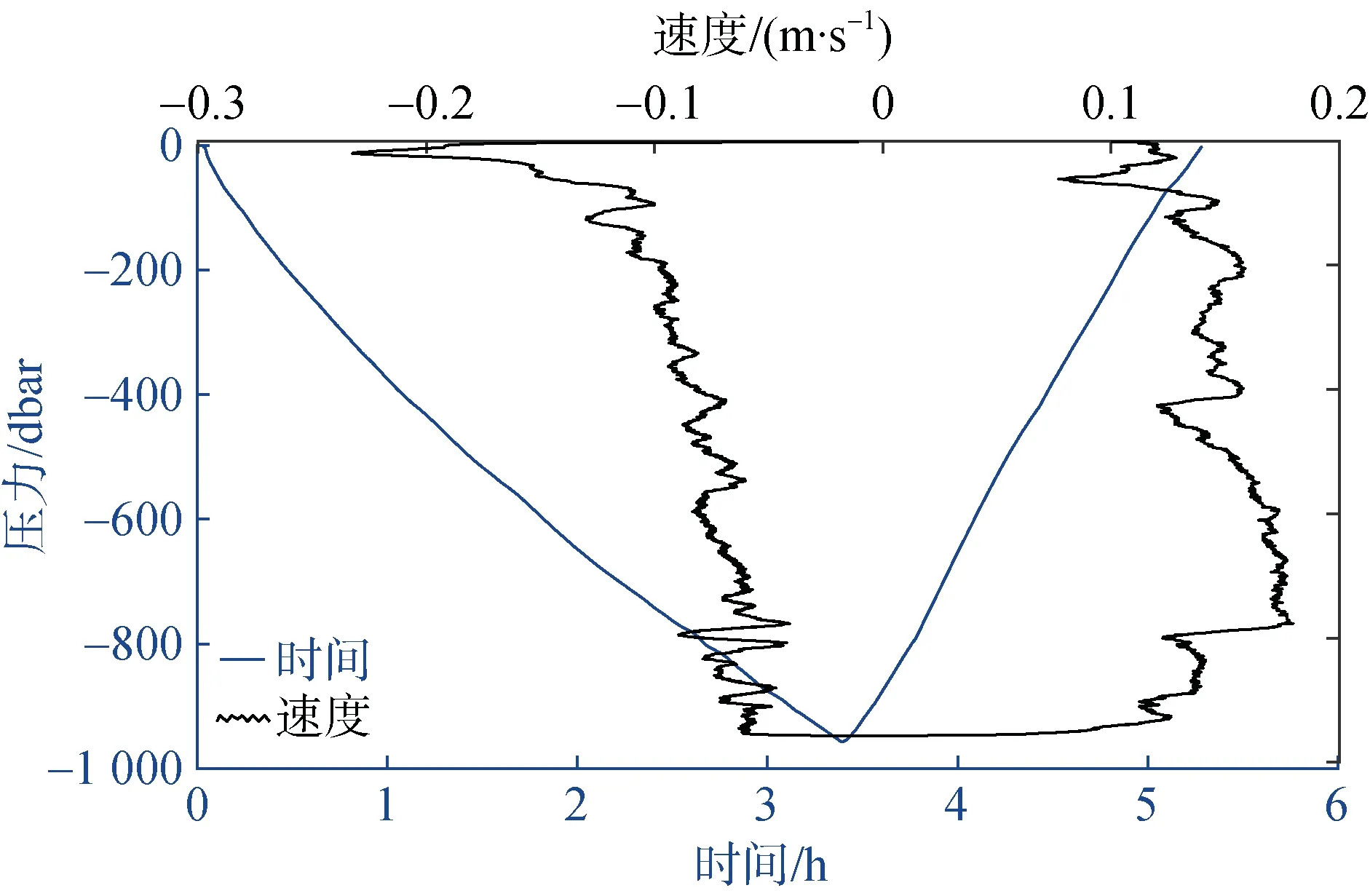
图2 水下滑翔机垂直速度与时间随压力的变化Fig. 2 Glider vertical speed and time changes with pressure

根据公式(1)—(4), 我们计算933组剖面数据的理论出水速度与实际出水速度, 如图3, 在12月25日前计算理论速度与实际速度相差不大, 表明流场较弱, 在12月30日后理论速度与实际速度相差较大,表明该段时间流场变化较大, 这是由于随着季风转换, 冬季南海北部盛行东北风使得南海北部存在一支东南向的沿岸流, 该沿岸流沿着南海北部流经西沙群岛随后沿越南东岸向南一部分经海峡流出南海, 一部分向东流入南海南部, 同时由于西沙群岛地理环境影响, 西传的中尺度涡能量经背风波及次中尺度过程耗散, 使得该区域流场环境复杂。在观测期间一个冷涡自东北向西南经过西沙群岛并在越南东岸耗散(图4), 通过改变观测路径, 该水下滑翔机于1月3日—2月16日自南向北穿过冷涡, 我们根据式(1)—(5)计算其深度平均流, 为了验证深度平均流的准确性, 我们假定水下滑翔机下潜最大深度为零动力面, 并在深度上获得平均地转流, 结果显示纬向深度平均流及地转流相关系数达到0.95, 表明水下滑翔机获得深度平均与地转流的一致性, 其不同可能来自深度平均流误差、海洋高频信号及零动力面的选取, 因此下文将利用水下滑翔机获得的深度平均流计算中尺度涡的绝对地转流。

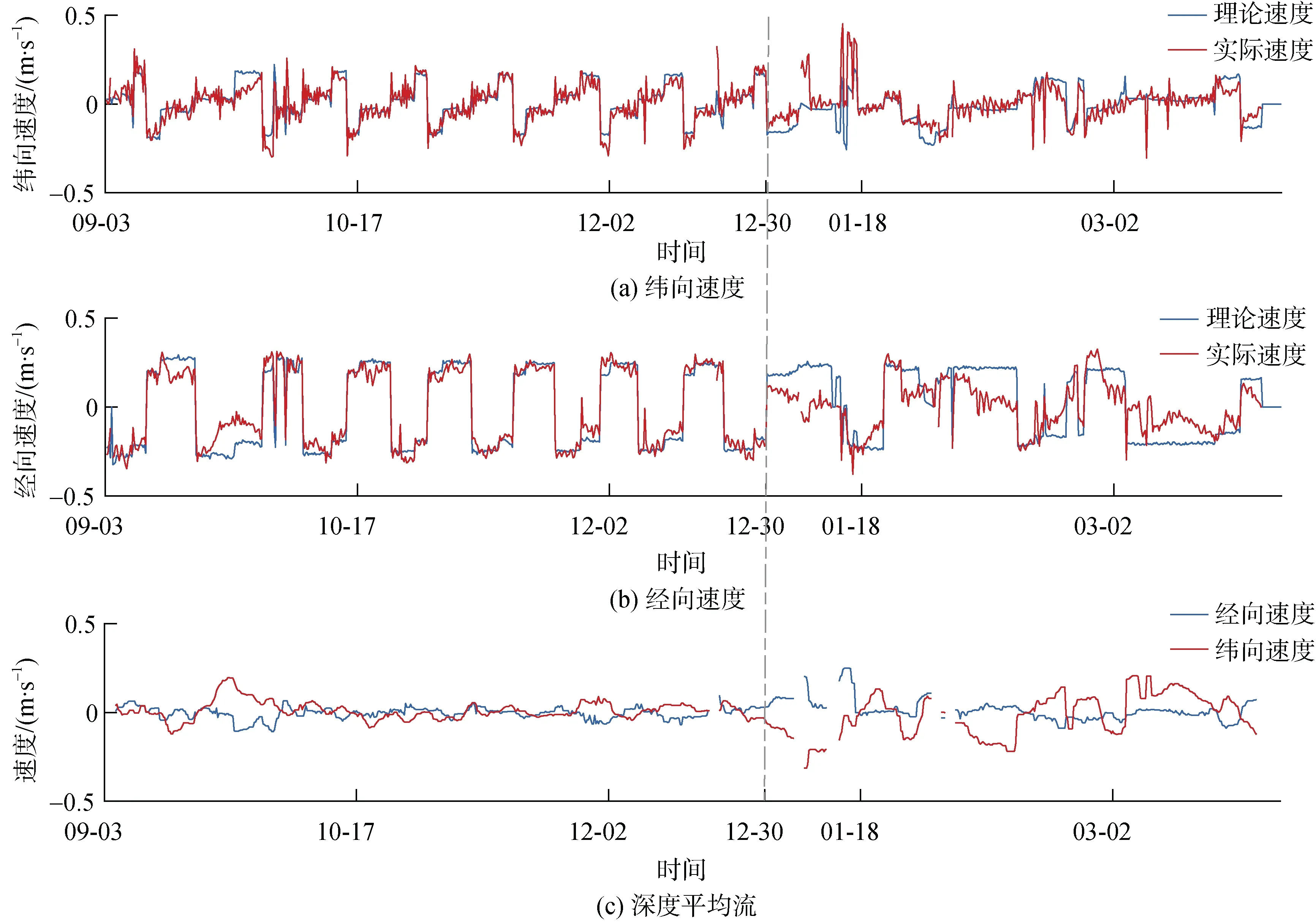
图3 水下滑翔机计算深度平均流Fig. 3 Depth average current calculated from the glider’s observation

2.2 误差分析

深度平均流的误差受GPS定位误差、依靠水下滑翔机浮力、俯仰、横滚和航向模拟获得理论水动力模型误差、CTD、压力传感器精度误差等多种因素影响, 考虑到可能存在的潜在误差, 我们采用校正船载ADCP观测数据方法定量分析深度平均流误差。由于船载ADCP直接获得海水相对于船体的流速, ADCP坐标系与船体坐标系的相对偏差会导致测量流速和大小的误差, 为了消除这种误差, Joyce采用一组坐标变化α、β去除航向产生的角度误差和噪声, 其真实水速由船速与修正后ADCP测量水速之差得到[15]。基于以上原理, 我们假定水下滑翔机按航行路径航行, 在每一次转弯前后测量的流速相同(图5), 为了排除海洋高频信号影响, 我们对数据做如下处理: 1) 48小时低通滤波深度平均流; 2) 对转弯前后5个剖面数据平均;3) 剔除单次转弯俯冲角度相对于水面大于55°的数据; 4) 剔除在转弯前或转弯后单次位移角度大于20°的数据; 5) 剔除GPS数据信号丢失数据。在做以上处理后, 我们共获得23次转弯数据, 其中3组转弯由于误差过大被排除, 基于Joyce的方法,我们假定水下滑翔机获得误差可以通过一组坐标变化修正[15-16], 即:

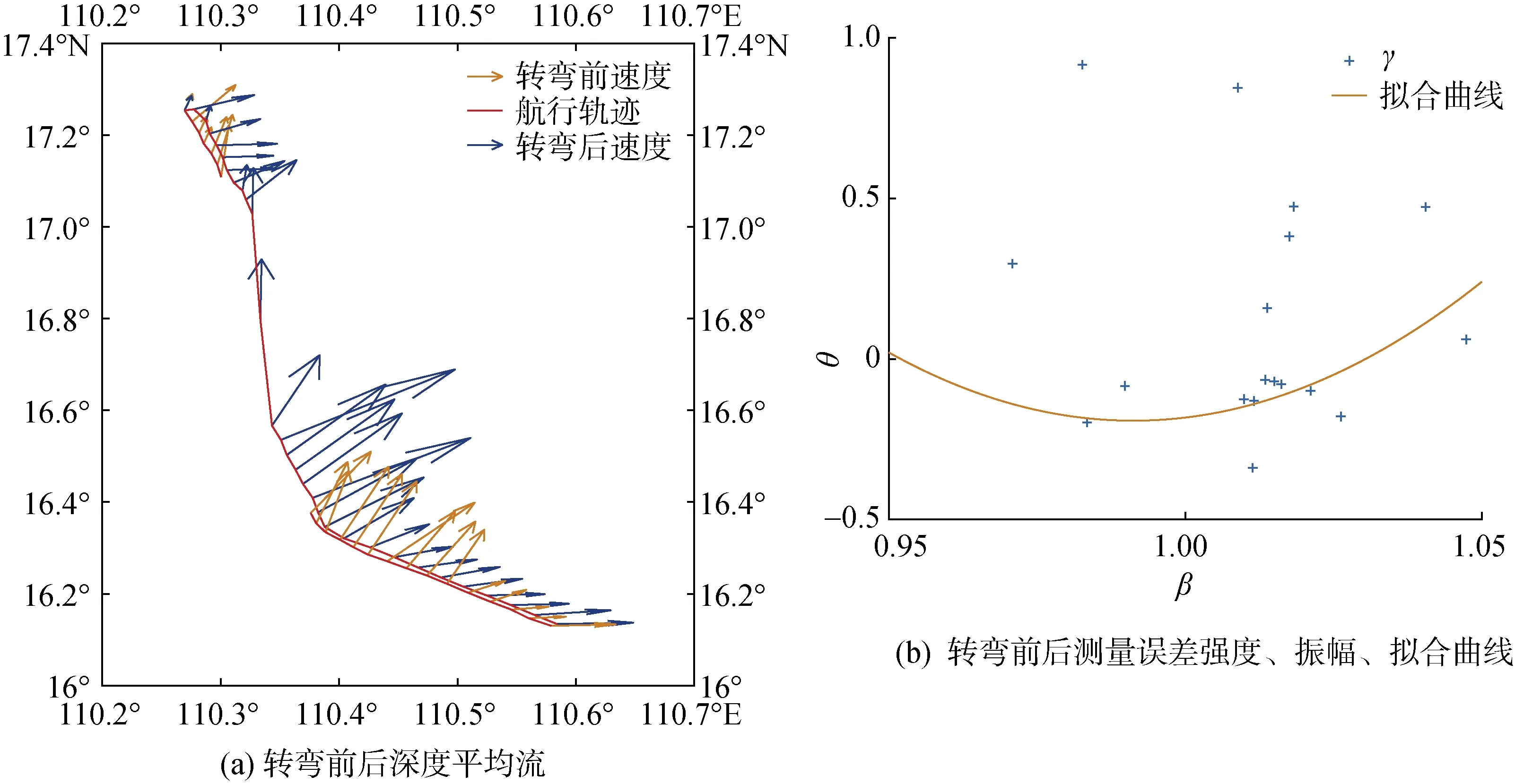
图5 转弯前后深度平均流及测量误差强度、振幅、拟合曲线Fig. 5 Depth average current, observation error intensity, amplitude, and fitting curve before and after the glider turns

其中,ug1、ug2为水下滑翔机转弯前后深度平均流,ur为实际流速, 假定海洋流速恒定以及滑翔机测量没有误差, 则γ恒等于1, 若存在测量误差, 则测量误差受测量角度和测量误差强度β影响，定义误差：

根据以上公式, 我们计算20组水下滑翔机转弯误差强度和角度(表1), 振幅β表明深度平均流计算过高估计0.01 m/s, 误差精度约为0.036 m/s, 低于其他作者描述精度, 这可能是由于 1) 没有对GPS进行磁力校正; 2) 长时间投放水下滑翔机使得测量精度产生漂移; 3) 长时间断面观测使得转弯前后数据过少。

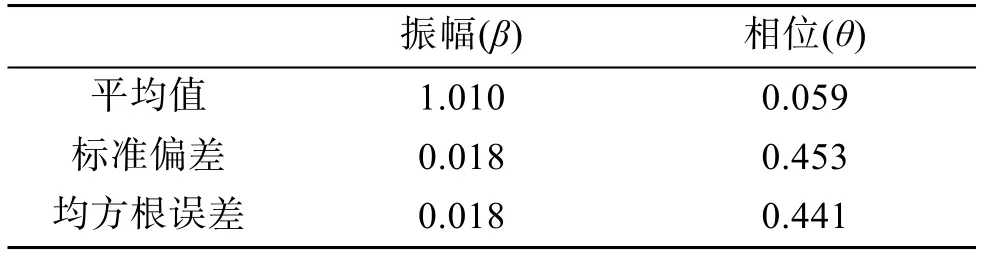
表1 误差强度振幅与相位Tab. 1 Error intensity and phase

2.3 绝对地转流

利用深度平均流以及热成风公式, 我们计算水下滑翔机穿越冷涡时的绝对地转流, 如图6, 水下滑翔机自南向北穿过冷涡(图4), 受观测计划影响, 冷涡外围观测密度较大, 绝对地转流显示出冷涡特征,在15.95°N以南, 绝对地转流为东向流, 速度剪切在上层500 m较强, 在500米以下较弱, 最大流速约为0.48 m/s, 最大深度处平均流速约为–0.015 m/s, 在15.95°N 以北, 绝对地转流为西向流, 地转流速稍弱于冷涡南侧, 冷涡最大深度到达500 m, 最大流速约为0.47 m/s, 最大深度处平均流速约为–0.028 m/s, 最大深度处速度受地转影响在冷涡南部为东向流, 在冷涡北部为西向流。根据式(10), 绝对地转流包含利用温盐计算获得斜压地转流及利用深度平均流计算获得水下滑翔机最大深度处正压地转流, 因此相比绝对地转流, 利用零动力面假设获得相对地转流计算流量将产生一定输送误差(如假定获得最大深度处速度精度为0.03 m/s在水平100 km和水深1 000 m尺度上会产生3 Sv 输送误差)。

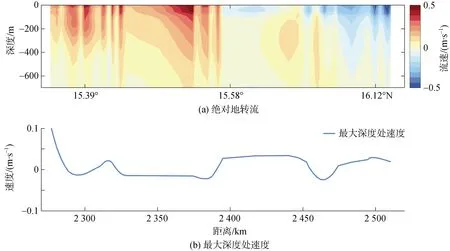
图6 纬向绝对地转流和纬向最大深度处速度Fig. 6 Zonal absolute geostrophic current and zonal maximum depth velocity

3 总结

利用水下滑翔机观测温盐及经纬度数据可以计算深度平均流, 其计算是根据GPS理论出水速度与实际水下滑翔机出水速度之差获得, 本文利用中国科学院沈阳自动化研究所海翼水下滑翔机在南海西沙群岛附近获得的温盐剖面数据评估深度平均流,并利用地转流数据验证深度平均流的准确性, 结果显示深度平均流与深度平均地转流相关系数达到0.95,表明流场的一致性, 假定水下滑翔机在每次转弯前后速度一致, 其误差可以用船载ADCP校正法做误差分析, 结果显示深度平均流计算误差高约0.01 m/s,精度约为0.036 m/s 低于其他作者计算精度, 其原因可能是用于未修正的GPS 精度以及西沙群岛复杂流场导致, 未来应考虑对照ADCP数据对深度平均流做进一步精度分析; 利用深度平均流可以计算最大深度处地转速度, 从而计算绝对地转流, 本文利用水下滑翔机穿越一个冷涡并计算穿越冷涡时水下滑翔机获得的绝对地转流, 结果显示冷涡南部绝对地转流速略大于冷涡北部, 在冷涡南部绝对地转流及最大深度处流速为东向流, 流核在表层至500 m处, 在冷涡北部绝对地转流及最大深度处流速为西向流, 流核在上层300 m处, 受观测计划及地转流速影响, 冷涡外围观测密度较大。

水下滑翔机作为一种新型观测载体, 其具有高精度、长时间的观测优势, 使得其正越来越多的应用在世界各大洋尤其边界流区域, 然而受流场以及海洋生物影响, 需对观测数据做有意义的数据预处理, 利用更加严格、标准化的数据将提高水下滑翔机的可应用性, 尤其在边界流区域, 考虑到计算的深度平均流精度以及观测样本间隔问题, 本文未对流量做出估计。