双组分层撞击流反应器流场振荡特性研究

张建伟, 阚延勇, 董 鑫, 冯 颖

双组分层撞击流反应器流场振荡特性研究

张建伟, 阚延勇, 董 鑫, 冯 颖

(沈阳化工大学 机械与动力工程学院, 辽宁 沈阳 110142)

为了研究双组分层撞击流流场振荡特性，选用大涡模拟对反应器内流场进行分析，通过分析一次和二次撞击区域的运动情况，获得了不同进口雷诺数、不同喷嘴间距、喷嘴边界受限程度下撞击面偏斜振荡规律。结果表明，二次撞击后的轴向速度与径向速度分布呈双峰形式，轴向速度与径向速度随雷诺数的增大而增大。二次撞击面发生偏斜振荡，偏斜振荡周期随喷嘴间距增大而增大，随进口雷诺数增大而减小。喷嘴间距越小，偏斜振荡周期对喷嘴边界受限程度越敏感。基于数值模拟结果，得出偏斜振荡周期与各因素之间的无量纲关联式，关联式计算结果与数值模拟值吻合较好，可以很好地预测二次撞击偏斜振荡周期。

撞击流；二次撞击；偏斜振荡；振荡周期；大涡模拟

1 前言

撞击流(impinging stream，IS)概念最早由Elperin[1]提出，其中心思想指气—固两相流体相向高速运动进行撞击，形成一个高剪切速率与高湍流的撞击区，以此实现热、质传递的强化。众多学者[2-5]对其相关化工过程进行研究，证明了撞击流可以提高传递过程的相间传递系数几倍到几十倍不等。

大量研究表明[6-11]，反应器撞击区流体流动行为与混合效果紧密相关，而其中撞击面的稳定性起重要作用，因此，近年来关于撞击流反应器撞击面的研究成为重点。Tomac等[12]在研究混合室中相互撞击的双射流的振荡特性时，证明了混合室振荡行为的存在，并且解释了振荡行为的存在是由于不稳定的冲击区域和来自壁面的压力反馈所产生的涡。Li等[13]采用平面激光诱导荧光技术(PLIF)研究改变结构参数下的T型反应器半偏转振荡对反应器混合的影响。Hao等[14]运用粒子图像测速技术(TR-PIV)对不同雷诺数下的双腔通道振荡进行研究，结果表明振荡的剧烈程度与雷诺数有关。Kiyan等[15]对撞击驻点的偏移量进行研究，发现驻点偏移量随着出口速度比的减小而线性增加，且撞击面向射流速度较小的一侧偏移。Tu等[16]利用粒子成像测速系统和高速摄像机对激励下的T型反应器的振荡行为进行了研究，结果表明，反应器的结构参数对其振荡行为有显著影响，且撞击面激励振荡幅值随雷诺数和激励幅值的增大而增大，随激励频率的增大而非单调递减。许鑫磊等[17]通过实验和模拟研究T型反应器非稳态吞噬流机理，结果表明，大涡模拟能较好地对非稳态吞噬流的振荡特性进行预测。以上单层对置撞击流反应器更多关注流场分布和流动形态等对混合效果影响的研究，本工作在反应器流动特性研究基础上，设计了新型双组分层撞击流反应器，对二次撞击面的振荡特性进行研究。

本工作利用大涡模拟对双组分层撞击流反应器内流场进行研究。通过比较不同时刻下相同雷诺数和不同雷诺数反应器内速度分布规律，考察二次撞击区域的振荡形式及其周期性变化，分析二次撞击偏斜振荡周期变化规律与喷嘴边界受限程度的变化，建立偏斜振荡周期无量纲关联式。本研究成果可为多层撞击流反应器的结构优化提供参考依据。

2 数值模拟

2.1 物理模型

双组分层撞击流反应器的物理模型结构如图1所示，反应器高度500 mm，内径130 mm，反应器上部设直径40 mm的出口，出口中心距反应器顶部30 mm，喷嘴采用上下两组对置放置，上层喷嘴距反应器顶部130 mm，下层喷嘴距反应器顶部为230 mm，取反应器底部中心为坐标原点，喷嘴轴线为轴，水平向右为正方向，轴正向向上，轴正向向里，选取直角坐标系，如图1所示(面)。4个喷嘴直径相同，取=10 mm，为喷嘴间距(mm)。

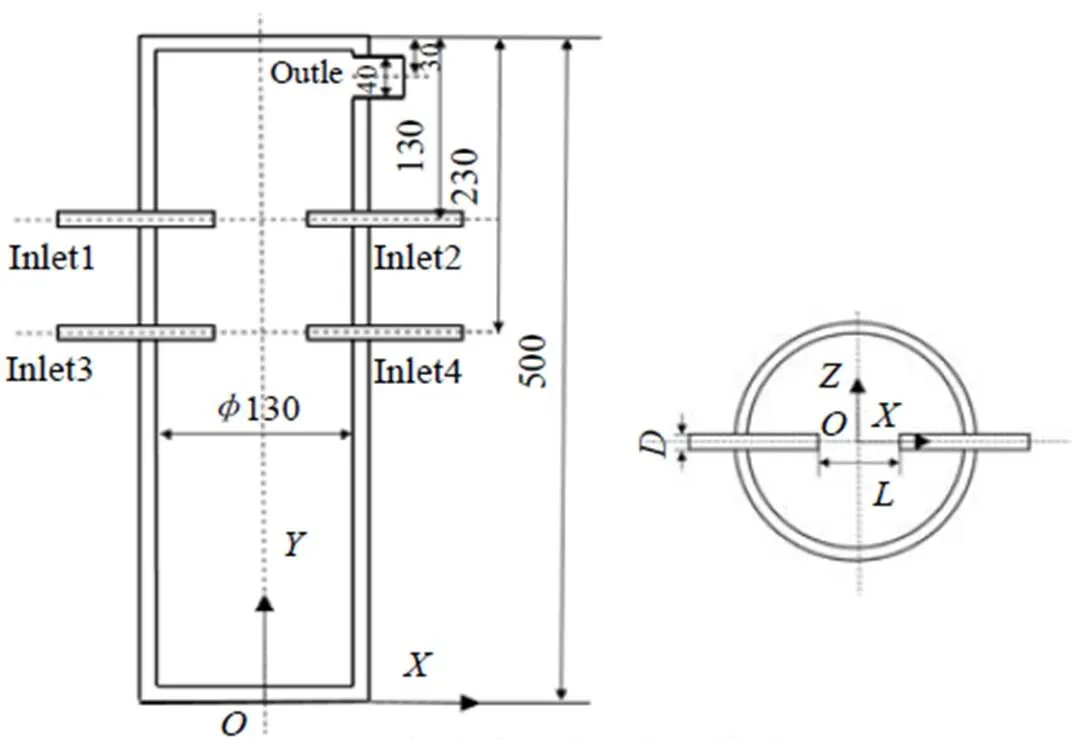
图1 撞击流反应器物理模型

模拟具体工况如表1所示，表中/为喷嘴边界受限程度。其中雷诺数用式(1)计算

表1 模拟条件下的工况

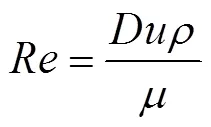
式中：为射流进口流速，m×s-1；为密度，=0.997×103kg×m-3；为黏度，=1.005×10-3Pa×s。

2.2 网格划分与计算区域

采用非结构化网格对上层、下层流体撞击区域进行局部网格加密。为了确保模拟结果对网格无依赖性，分别采用538 294、928 879、1 161 898、1 294 290网格模型对下层喷嘴轴线的速度分布进行计算，如图2所示。当网格数达到1 161 898后，数据误差在8% 以内。因此，在保证模拟准确性和计算时间的情况下，选用网格数量为1 161 898的数值模型进行计算。

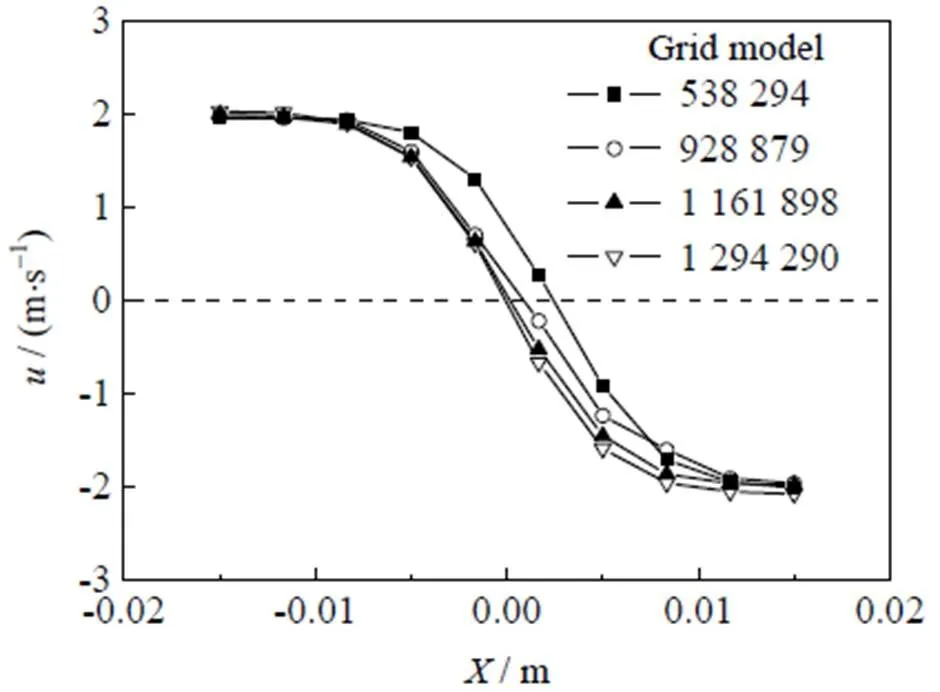
图2 不同网格数量的模拟结果

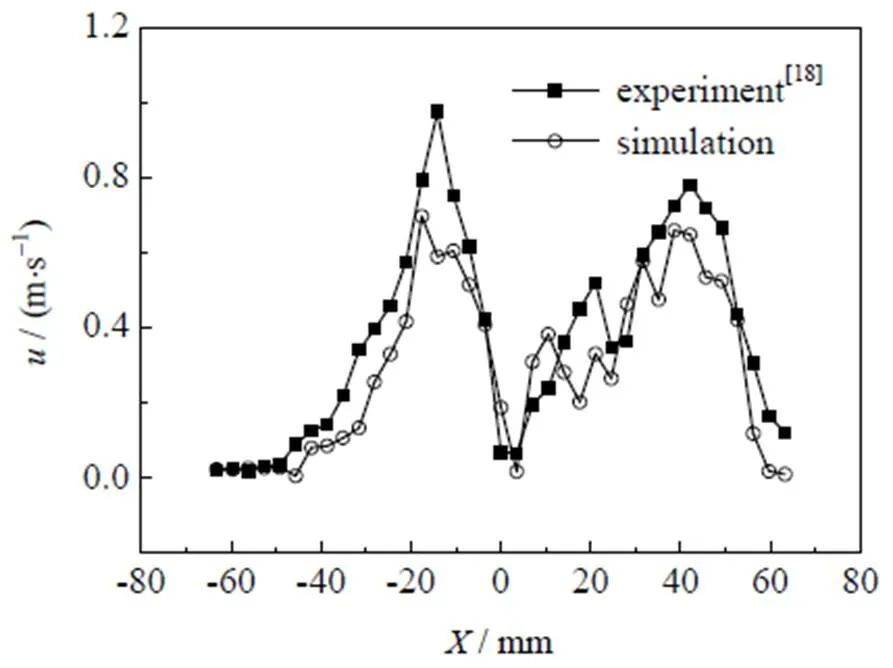
图3 轴向速度分布

为了进一步确保模拟的准确性，对模型进行验证，以喷嘴间距30 mm、喷嘴直径=10 mm、雷诺数=16 000的工况下进行模拟，模拟结果与张建伟等[18]实验工况数据比较如图3所示，由图可见，计算模拟值与实验数据的相关系数为0.920 2，说明模型具有可靠性。选取二次撞击面上的点A为速度的监测点，三维坐标分别为A(5,320,0)，如图4所示。

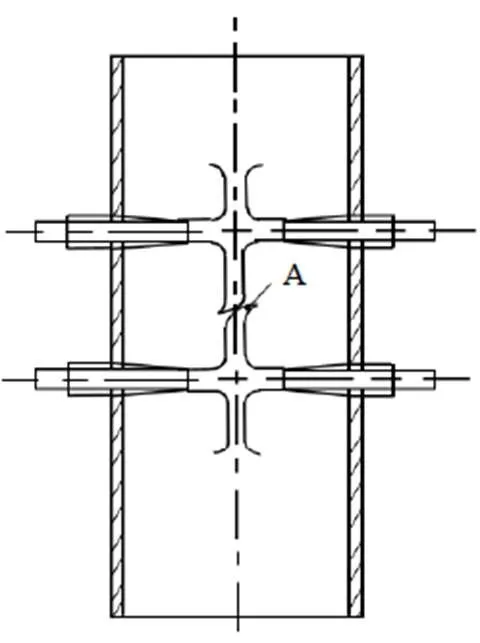
图4 测量位置示意图

2.3 边界条件与模拟方法

模拟采用的流体介质为20 ℃水，流体进口边界为“Velocity inlet”，反应器进口速度波动采用涡方法，根据文献[19]以及模拟验证，所加涡数量设置为200个；相对湍流强度为默认设置；出口为“Pressure outlet”压力出口，其余反应器边界均为默认设置。

大涡模拟能直接计算在湍流流场中起主导作用的大尺度涡旋结构，而仅对小尺度涡旋结构做模型假定，且能模拟撞击面摆动现象[20]。屠功毅等[21]运用大涡模拟研究了平面撞击流反应器的振荡特性，通过实验与模拟的对比，验证了大涡模拟湍流模型对撞击流振荡研究的准确性。为了研究双组分层撞击流反应器的振荡特性，本研究选用Fluent软件中的大涡模拟(large-eddy simulation，LES)湍流模型和动态Smagorinsky-Lilly亚格子模型，模型常数s为0.1。

在湍流流场中大尺度涡旋结构起主导作用，而湍流动量的扩散主要由小尺度涡旋结构所决定。大涡模拟方程通过在傅里叶或空间域不可压缩流体的N-S方程过滤掉时间项得到，在计算中，可以有效地滤掉小于过滤网格的涡旋结构，从而得到大涡的以下方程：

质量守恒方程：

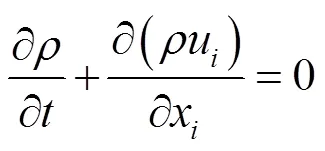
动量守恒方程：

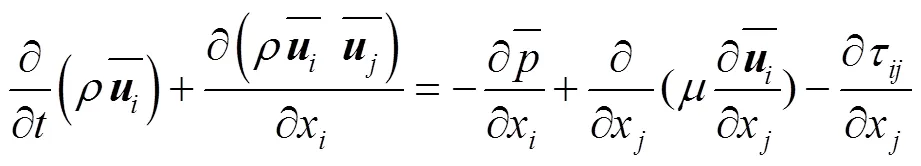
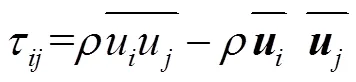
亚格子应力普遍用涡黏性假设，定义为

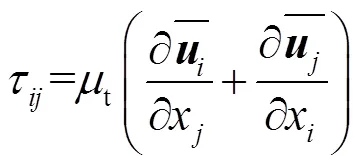
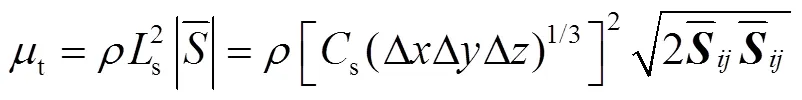
其中，

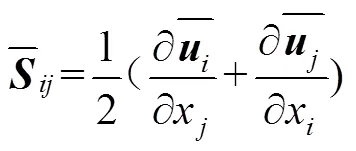
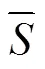
采用SIMPLE方法作为压力-速度耦合，采用Least Squares Cell Based方法作为空间离散梯度方法，采用Standard方法作为压力求解，采用QUICK型式作为动量求解方法，采用Second Order Implicit求解作为瞬态方程式，时间步长为0.001 s，每时间步长迭代20次，收敛标准为连续性方程，残差值控制在10-3，其余方程残差值控制在10-5。

2.4 偏斜振荡周期无量纲关联式

为了更准确比较不同喷嘴间距、不同雷诺数和喷嘴边界受限程度下的双组分层撞击流反应器偏斜振荡量纲1周期差异，用函数关系式表示偏斜振荡量纲1周期/(/)(表示偏斜振荡周期，s)。影响偏斜振荡周期变化的主要因素为：两水平喷嘴间距与喷嘴直径比(/)、进口雷诺数和喷嘴边界受限程度。采用无量纲分析法，确定偏斜振荡量纲1周期与各因素之间的关系式：

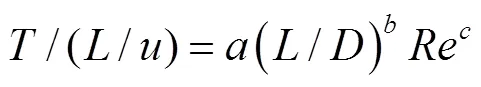
式中：为待定系数，利用模拟数据进行拟合确定系数，从而得到偏斜振荡周期无量纲关联式。

3 结果与讨论

3.1 撞击流反应器速度分布规律

上下两层喷嘴流体水平碰撞形成一次撞击，由一次撞击形成的上下径向射流竖直碰撞形成二次撞击，如图4所示。为分析进口雷诺数=16 000条件下撞击流反应器内流场速度分布规律，得到面速度分布云图，如图5所示。二次撞击区的两股相向流体相互作用会产生偏斜的现象，并且随着时间的变化，径向射流呈“S”形摆动。

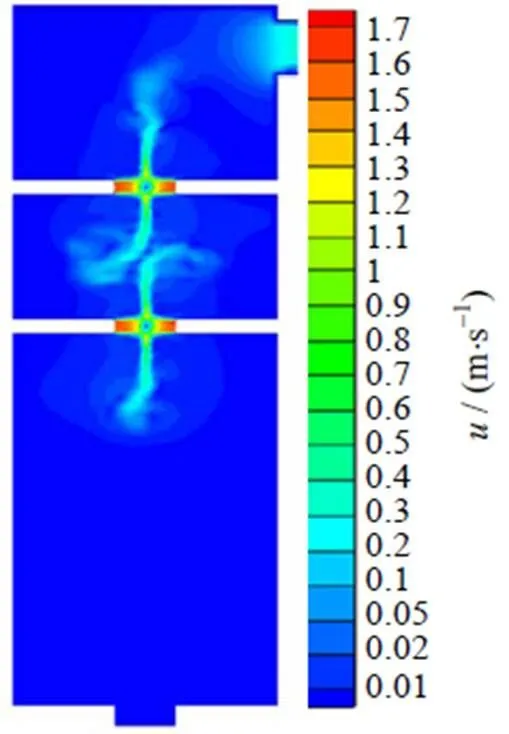
图5 双组分层撞击流反应器速度分布云图

为进一步分析二次撞击区的速度分布，图6为撞击流反应器在不同雷诺数下轴向速度分布和径向速度分布。由图6(a)和(b)可知，随着雷诺数的增大，整个流场的速度分布都随之增大。而从图6(a)可知，速度在撞击中心处最低，原因是撞击中心处压力最大，沿撞击中心向左右两侧流体速度表现为先增大后减小然后缓慢增大再减小，整体速度分布呈双峰形式，这是因为撞击中心处压力向四周释放以及反应器器壁阻碍的作用。从图6(b)可知，二次撞击中心处速度损耗量较大使得其速度最小，而此时速度较小位置为一次撞击中心处，且其速度大于二次撞击中心处速度，整体速度分布也呈双峰形式，并且图6(b)的径向速度变化规律性更强。

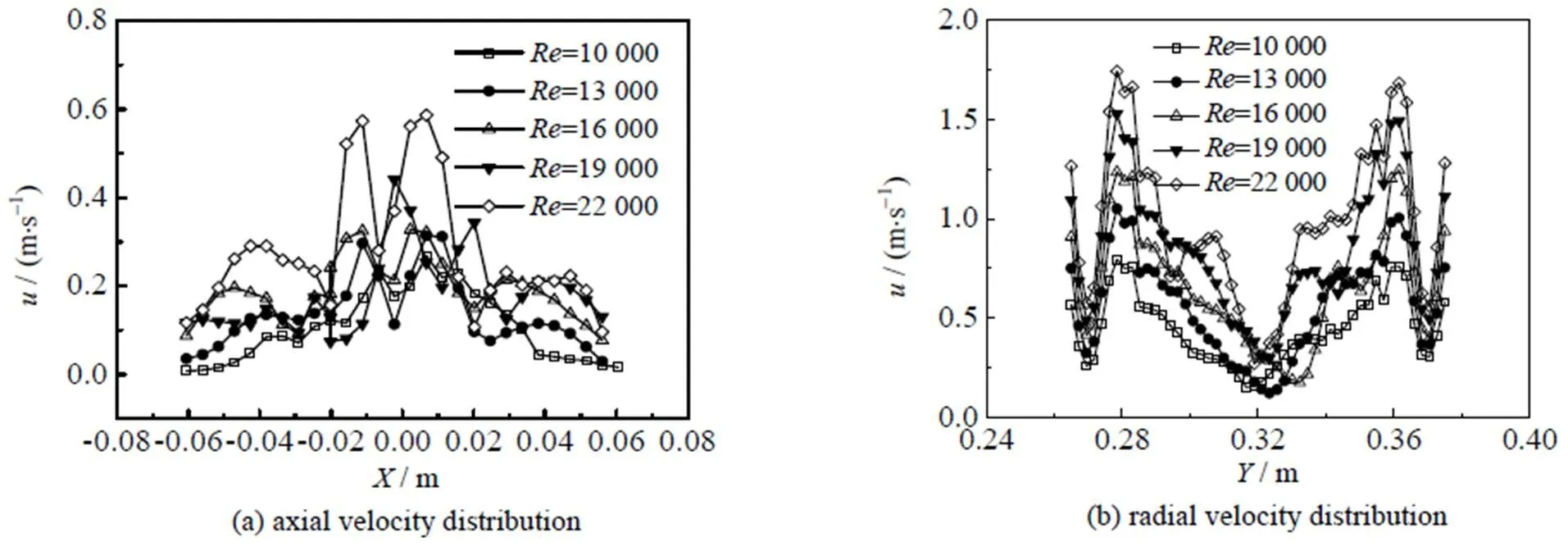
图6 不同雷诺数下XOY面轴向速度分布和径向速度分布

图7为=16 000下面不同时刻下径向速度分布，从图7可知，一次撞击中心处速度波动较小，为3.9%，而二次撞击中心处速度波动较大，为58%，主要是二次撞击区域流体卷吸和撞击面偏斜共同作用的结果。

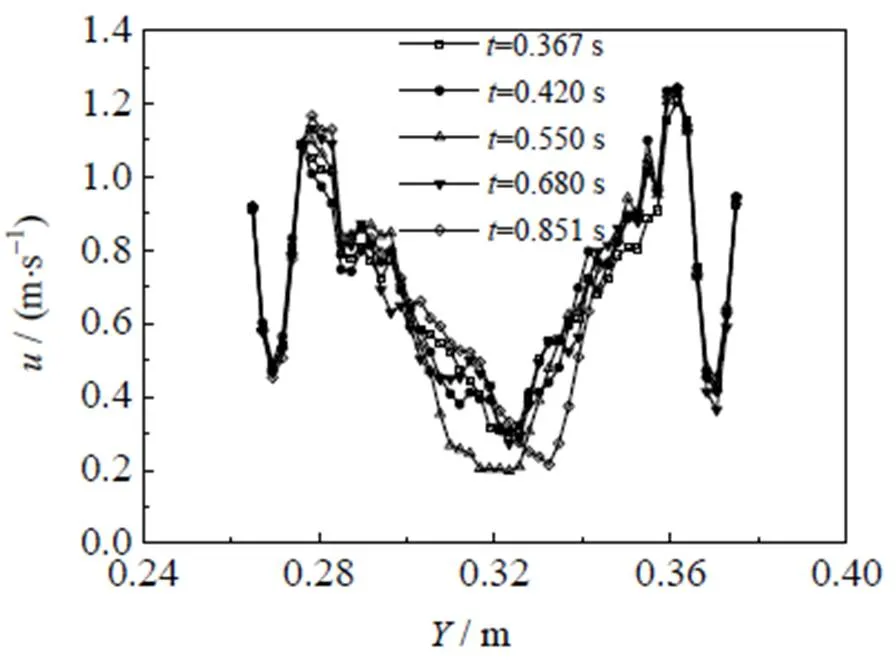
图7 XOY面不同时刻径向速度分布

3.2 撞击流反应器二次撞击区振荡特性

图8给出了雷诺数=16 000，两喷嘴水平间距=3时不同时刻双组分层撞击流反应器流场变化的速度云图。从图8可知，两股径向流体首先在二次撞击中心处相互偏斜，随即在撞击中心处碰撞，然后流体相互反向偏斜，最后再相互碰撞，往复循环完成一个周期，这种撞击模式称为偏斜振荡[23]。所以二次撞击面处是偏斜振荡，并且偏斜振荡存在固定的周期。利用流场中的速度场能很好说明偏斜振荡运动过程[24]，偏斜振荡周期能反映速度的变化规律，准确地描述偏斜振荡特性。屠功毅等[23]对水平对置撞击流反应器振荡特性进行研究，发现偏斜振荡周期能较好地解释偏斜振荡这一撞击模式，因此可以利用偏斜振荡周期分析偏斜振荡特性。

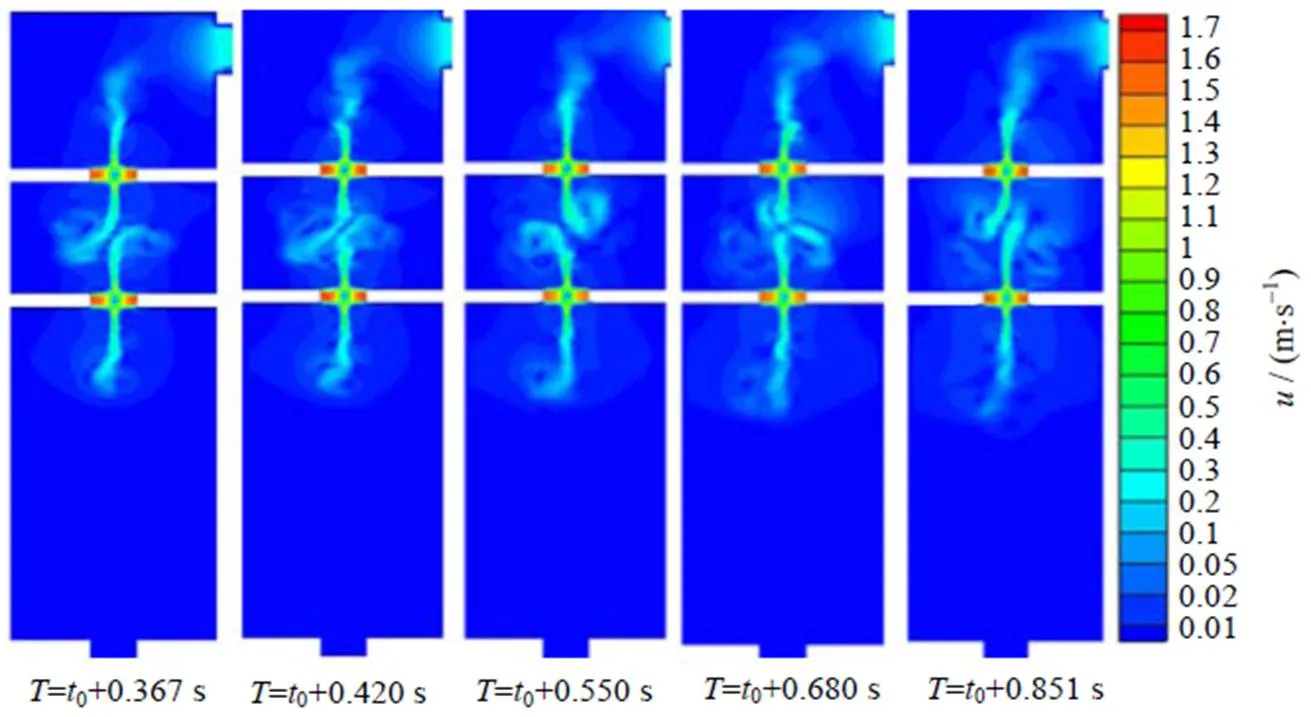
图8 Re=16 000时XOY面的速度云图

通过对图4的A点进行速度监测，发现A点速度随时间变化具有周期性，原因为2股径向射流周期性产生相互偏斜撞击。如图9为雷诺数=16 000，两喷嘴水平间距=3的工况下，A点速度随时间变化情况，相邻两峰之间为一个周期，图中周期为0.48 s。

图9 A点速度随时间变化

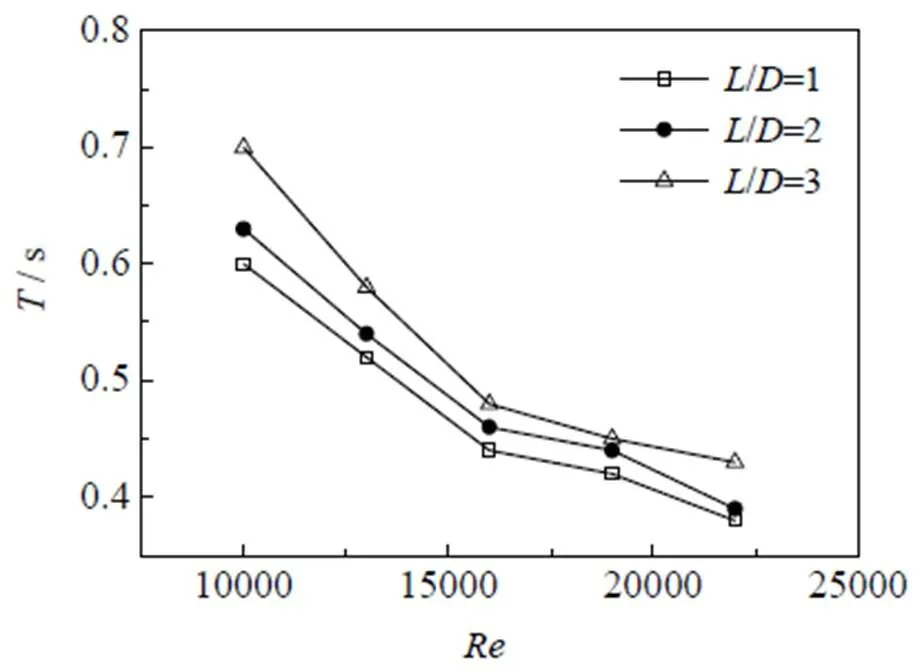
图10 偏斜振荡周期分布

为了研究二次撞击面偏斜振荡周期分布，对A点速度进行监测，得到不同喷嘴间距下，二次撞击偏斜振荡周期随进口雷诺数的变化，如图10所示。当喷嘴间距相同时，随进口雷诺数增大，偏斜振荡周期逐渐减小，而当进口雷诺数相同时，随着喷嘴间距增大，偏斜振荡周期逐渐增大。其中当喷嘴间距为/=3，进口雷诺数从10 000增加到22 000时，偏斜振荡周期减小最多，为38.6%，说明进口雷诺数对偏斜振荡周期影响明显。

偏斜振荡周期会受到撞击流喷嘴边界受限程度/的影响[21]，如图11所示为偏斜振荡周期随/的变化规律，相同喷嘴间距下随着/增大，偏斜振荡周期逐渐增大。不同的喷嘴间距下随着两喷嘴间距减小，与/逐渐增大，说明对/的变化变得敏感。

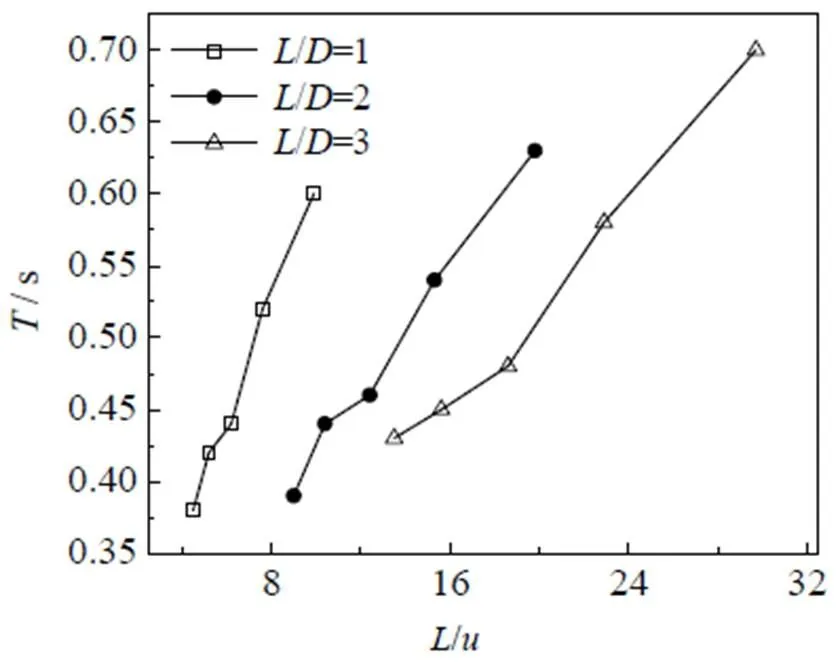
图11 偏斜振荡周期随L/u的变化

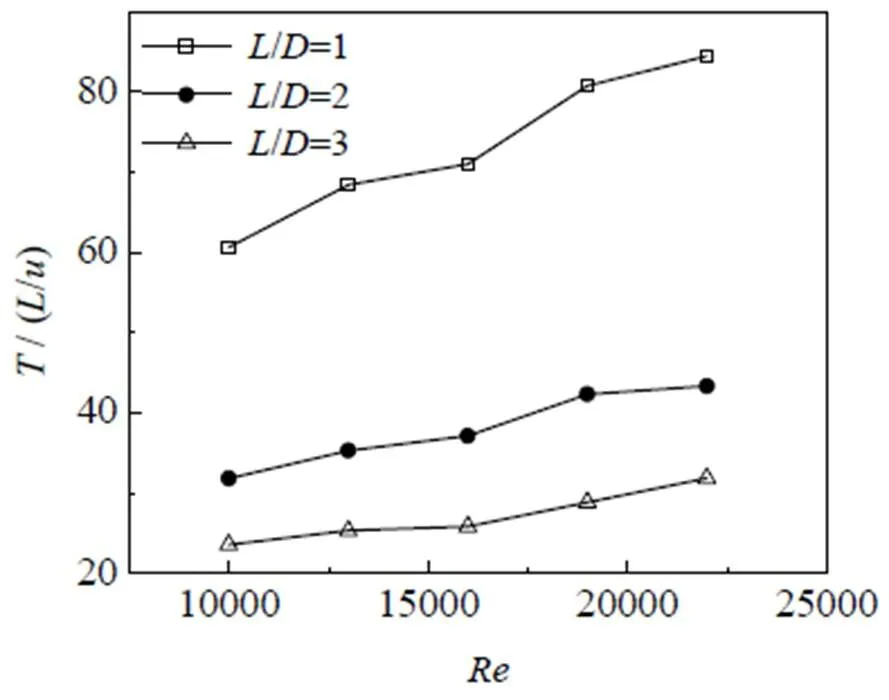
图12 T/(L/u)随进口雷诺数的变化

如图12所示为偏斜振荡量纲1周期与各影响因素的关系。当喷嘴间距与喷嘴直径比相同时，随着进口雷诺数的增大，/(/)逐渐增大，当进口雷诺数相同时，随着喷嘴间距与喷嘴直径比增大，/(/)逐渐减小，而/=1时，/(/)较大，原因为此时喷嘴间距最小，喷嘴边界处流体受限最为明显。

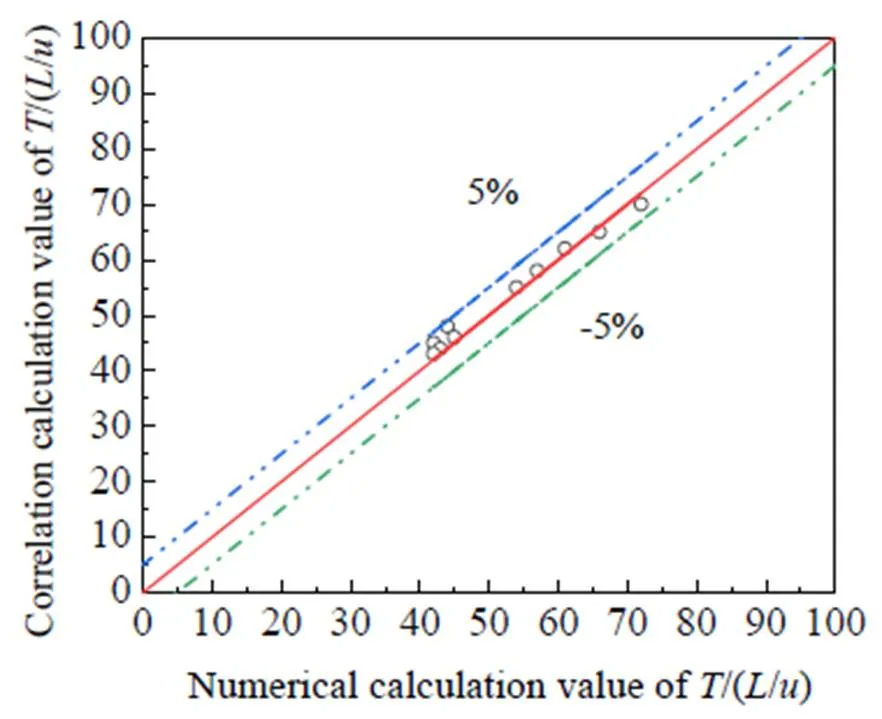
图13 T/(L/u)的关联式计算值与数值计算值对比

3.3 二次撞击偏斜振荡周期无量纲关联式

二次撞击偏斜振荡周期的影响因素有、/和/。因此，对图12中/(/)数据点用式(8)进行拟合，确定待定系数、、，得到其无量纲关联式为：

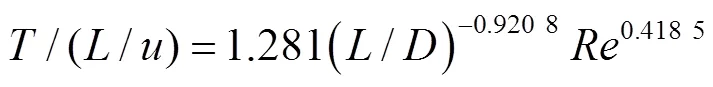
关联式计算结果与数值计算值对比如图13所示，由图可见，/(/)的无量纲关联式计算结果与数值计算值吻合较好，可以准确地预测偏斜振荡周期变化。

4 结论

采用CFD软件Fluent，对新型双组分层撞击流反应器的振荡特性进行数值模拟。对不同雷诺数下撞击流反应器流场速度分布进行了研究，得到如下结论：

(1) 双组分层撞击流反应器的速度分布规律：轴向速度与径向速度分布呈双峰形式，且随着进口雷诺数的增大，轴向速度和径向速度逐渐增大，二次撞击面处振荡为偏斜振荡。

(2) 通过对不同雷诺数和不同喷嘴间距下的偏斜振荡进行研究，二次撞击偏斜振荡周期随两喷嘴间距增大而增大，随雷诺数增大而减小，两喷嘴距离越小，二次撞击偏斜振荡周期对喷嘴边界受限程度越敏感，且二次撞击偏斜振荡周期无量纲关联式与数值计算值吻合较好。

[1] ELPERIN I T. Heat and mass transfer in opposing currents [J]. Journal of Engineering Physics, 1961, 6(6): 62-68.

[2] YANG P F, LUO S, ZHANG D S,. Extraction of nitrobenzene from aqueous solution in impinging stream-rotating packed bed [J]. Chemical Engineering and Processing-Process Intensification, 2018, 124(6): 255-260.

[3] PAUL F, JÉRÔME G, ERIC G,. The potamochemical symphony: New progress in the high frequency acquisition of stream chemical data [J]. Hydrology and Earth System Sciences, 2017, 21(12): 1-41.

[4] CHANG J, JIA F K, SRINIVASAKANNAN C,. Impure ions removal from multicomponent leach solution of nickel sulfide concentrates by solvent extraction in impinging stream rotating packed bed [J]. Chemical Engineering and Processing - Process Intensification, 2019, 137(10): 54-63.

[5] DONG B, LI G, YANG X G. Controllable synthesis of (NH4)Fe2(PO4)2(OH) 2H2O using two-step route: Ultrasonic-intensified impinging stream pre-treatment followed by hydrothermal treatment [J]. Ultrasonics Sonochemistry, 2018, 42(7): 452-463.

[6] 汪铁林, 王博, 周玉新, 等. 撞击流反应合成纳米二氧化锡[J]. 化工进展, 2008, 27(11): 1832-1835, 1845.

WANG T L, WANG B, ZHOU Y X,. Synthesis of tin oxide nanoparticles by impinging stream reaction [J]. Chemical Industry and Engineering Progress, 2008, 27(11): 1832-1835, 1845.

[7] CHEN Z Y, LIU Y, ZHANG Y Z,. Ultrafine layered graphite as an anode material for lithium ion batteries [J]. Materials Letters, 2018, 229(10): 134-137.

[8] 祁贵生, 武晓利, 刘有智, 等. 超重力液相沉淀法制备纳米铁酸钴 [J]. 化工进展, 2018, 37(5): 1680-1686.

QI G S, WU X L, LIU Y Z,. Preparation of cobalt ferrite nanoparticles by high gravity liquid precipitation method [J]. Chemical Industry and Engineering Progress, 2018, 37(5): 1680-1686.

[9] PITT G J, MILLWARD G R. Coal and modern coal processing: An introduction [J]. Thermochimica Acta, 1981, 15(4): 186-219.

[10] 张建伟, 董鑫, 马红越, 等. 双喷嘴水平对置撞击流混合器内湍流流动及混沌特性[J]. 化工进展, 2015, 34(7): 1832-1840.

ZHANG J W, DONG X, MA H Y,. Turbulence flow and chaotic characteristic in the dual nozzle opposed impinging stream mixer [J]. Chemical Industry and Engineering Progress, 2015, 34(7): 1832-1840.

[11] MARIA I N, RICARDO J S, MADALENA M D,. Micromixing assessment of confined impinging jet mixers used in RIM [J]. Chemical Engineering Science, 2012, 74(15): 276-286.

[12] TOMAC M N, GREGORY J W. Oscillation characteristics of mutually impinging dual jets in a mixing chamber [J]. Physics of Fluids, 2018, 30(11): 117102.1-117101.14.

[13] LI W F, YAN W, TU G Y,. Experimental study about mixing characteristic and enhancement of T-jet reactor [J]. Chemical Engineering Science, 2016, 144(11): 116-125.

[14] HAO F, HE C X, LIU Y Z. Self-sustained oscillation of the flow in a double-cavity channel: A time-resolved PIV measurement [J]. Journal of Visualization, 2020, 23(4): 245-257.

[15] KIYAN P, ESMAEIL E, UGUR A.. A numerical study of turbulent opposed impinging jets issuing from triangular nozzles with different geometries [J]. Heat and Mass Transfer, 2011, 47(4): 427-437.

[16] TU G Y, LI W F, QIAN W W,. Experimental study on oscillation behaviors in T-jets reactor with excitation [J]. Chemical Engineering Science, 2015, 134(3): 67-75.

[17] 许鑫磊, 严嘉玮, 张巍, 等. T型反应器内非稳态吞噬流机理[J]. 化工学报, 2018, 69(12): 5073-5080.

XU X L, YAN J W, ZHANG W,. Unsteady engulfment flow regime in T-jets reactor [J]. CIESC Journal, 2018, 69(12): 5073-5080.

[18] 张建伟, 马繁荣, 冯颖, 等. 双组分层不对称撞击流流场能量的研究 [J]. 高校化学工程学报, 2018, 32(4): 831-839.

ZHANG J W, MA F R, FENG Y,. Study on flow field energy of stratified asymmetric impinging flow of two groups [J]. Journal of Chemical Engineering of Chinese Universities, 2018, 32 (4): 831-839.

[19] MATHEY F, COKLJAT D, BERTOGLIO J P,. Assessment of the vortex method for large eddy simulation inlet conditions [J]. Progress in Computational Fluid Dynamics An International Journal, 2006, 6(1/2/3): 58-67(10).

[20] LIU Y, OLSEN M G, FOX R O. Turbulence in a microscale planar confined impinging-jets reactor [J]. Lab on A Chip, 2009, 9(9): 1110-1118.

[21] 屠功毅, 李伟锋, 黄国峰, 等. 平面撞击流偏斜振荡影响因素的大涡模拟[J]. 化工学报, 2013, 64(7): 2353-2359.

TU G Y, LI W F, HUANG G F,. Large-eddy simulation of influencing factors of deflecting oscillation of planar opposed jets [J]. CIESC Journal, 2013, 64(7): 2353-2359.

[22] SMAGORINSKY J. General circulation experiments with the primitive equations: I. The basic experiment [J]. Monthly Weather Review, 1962, 91(3): 99-164.

[23] 屠功毅, 李伟锋, 黄国峰, 等. 平面撞击流偏斜振荡的实验研究与大涡模拟[J]. 物理学报, 2013, 62(8): 346-353.

TU G Y, LI W F, HUANG G F,. Large-eddy simulation and experimental study of deflecting oscillation of planar opposed jets [J]. Acta Physica Sinica, 2013, 62(8): 346-353.

[24] 孙志刚, 李伟锋, 刘海峰, 等. 平面撞击流振荡特性[J]. 化工学报, 2009, 60(2): 338-344.

SUN Z G, LI W F, LIU H F,. Oscillation characteristics of two planar opposed jets [J]. CIESC Journal, 2009, 60(2): 338-344.

Study on flow field oscillation characteristics of two-component stratified impinging stream reactor

ZHANG Jian-wei, KAN Yan-yong, DONG Xin, FENG Ying

(School of Mechanical and Power Engineering,Shenyang University of Chemical Technology, Shenyang 110142, China)

Large eddy simulation was made to study the flow field oscillation characteristics of two groups of stratified impinging streams in the reactor. By analyzing the motion of the primary and secondary impinging regions, the deflection oscillation laws of the impinging surface under different Reynolds numbers, different nozzle spacing and nozzle boundary restriction (/) were obtained. The results show that the distribution of axial velocity and radial velocity after secondary impact was bimodal, and the axial velocity and radial velocity increased with the Reynolds number. The secondary impact surface had skew oscillation, and the skewed oscillation period increased with the increase of nozzle spacing and decreased with the increase of inlet Reynolds number. The smaller the nozzle spacing was, the more sensitive the deflection oscillation period was to the restriction degree of nozzle boundary (/). Based on the simulation results, the dimensionless correlation between the deflection oscillation period and various factors was obtained. The calculation results of the correlation are in good agreement with the simulation values, which can well predict the deflection oscillation period of secondary impact.

impinging stream; secondary impact; skew oscillation; oscillation period; large eddy simulation

TQ 021.1

A

10.3969/j.issn.1003-9015.2022.03.010

1003-9015(2022)03-0380-07

2021-05-27；

2021-08-23。

国家自然科学基金(21476141)；辽宁省兴辽英才计划(XLYC1808025)；中央引导地方科技发展专项(2020JH6/10500051)；沈阳市中青年科技人才项目(RC190323)。

张建伟(1964-)，男，辽宁义县人，沈阳化工大学教授，博士。

董鑫，E-mail：dongxin1106@syuct.edu.cn

张建伟, 阚延勇, 董鑫, 冯颖.双组分层撞击流反应器流场振荡特性研究 [J]. 高校化学工程学报, 2022, 36(3): 380-386.

：ZHANG Jian-wei, KAN Yan-yong, DONG Xin, FENG Ying. Study on flow field oscillation characteristics of two-component stratified impinging stream reactor [J]. Journal of Chemical Engineering of Chinese Universities, 2022, 36(3): 380-386.