考虑张拉的强度折减法在岩质边坡稳定性评价中的应用
2022-06-22陆嘉伟张继勋任旭华
张 辉,陆嘉伟,2,王 健,张继勋,任旭华
(1.河海大学水利水电学院,江苏 南京 210024;2.上海市政工程设计研究总院(集团)有限公司,上海 200092;3.中国一冶集团有限公司,湖北 武汉 430081)
0 引 言
含软弱夹层岩质边坡广泛存在于水利工程、矿业工程和交通工程等领域,其失稳会导致大量人员伤亡和经济损失。由于软弱夹层对岩质边坡的稳定性有着很大的影响,研究含软弱夹层岩质边坡的稳定性和破坏模式至关重要[1]。目前,边坡稳定分析使用较多的方法有刚体极限平衡法、极限分析法和强度折减法。刚体极限平衡法的物理意义明确,计算简单,但简化较多,没有考虑岩土体的变形,且需要预先假定滑动面。相对于刚体极限平衡法来说,极限分析法更严谨,假定合理,考虑了岩体的变形,但只能求出理想情况下的解析解,现实情况下很难有理想条件,在上限解和下限解相同的情况下,才能认为它的解是合理的。强度折减法最先于1975年被Zienkiewicz[2]提出,但受到当时计算机技术的限制,未被大规模采用,后来随着计算机技术的发展和数值计算理论的完善,这种方法越来越多的被应用[3]。强度折减法考虑了岩土体的变形,不需要假定滑动面,而且不受材料不均匀的限制。鉴于前2种方法的局限性,强度折减法越来越多地被运用到岩质边坡的安全稳定分析中。
长期以来,许多学者对岩质边坡稳定性进行了大量的研究。郑颖人等[4-5]提出的M-C等面积圆屈服准则,并成功应用于岩质边坡,认为边坡的贯通破坏是一个从局部剪切破坏逐步扩展到整体剪切破坏的渐进过程。吴顺川等[6]将基于遍布节理模型的强度折减法应用到岩质边坡中,提出通过剪应变速率判断最危险滑面,底部滑移面倾角与节理面等效内摩擦角基本一致。郭建军[7]采用双强度折减法,对黏聚力和内摩擦角进行单一变量折减,得到2个安全系数,根据2个安全系数的权重确定最终安全系数,认为随着边坡稳定性的降低,内摩擦角对坡体的稳定性影响程度增大,黏聚力对坡体稳定性的影响程度减小。王吉亮等[8]以乌东德电站右岸边坡为例,分析了边坡结构对边坡稳定性的影响和工程边坡的开挖对环境边坡的稳定性影响,认为顺向缓倾角岩质边坡变形破坏模式主要表现为顺层滑移,工程边坡的开挖可能引起环境边坡出现倾倒变形。靳晓光[9]以三峡库区边坡为例,通过三维有限元数值模拟,研究软弱夹层对岸坡岩体应力、位移的影响以及软弱夹层岩土体的位移特征,认为软弱夹层是顺向岩质边坡稳定的主要控制因素, 岸坡位移和应力随着软弱夹层的强度降低而显著增大。
上述学者利用强度折减法分析边坡稳定时大多只考虑抗剪强度的折减,但边坡的实际破坏过程中,某些部位主要表现为张拉破坏[10],因此岩土体的抗拉强度也会出现不同程度的折减。为此,本文基于FLAC3D软件,在传统强度折减法的基础上同时折减岩土体的抗拉强度,计算不同软弱夹层分布的岩质边坡的稳定性。根据不同折减系数塑性区分布的边坡的失稳破坏特征,以最大剪应变增量搜索滑动面,同时将该计算结果与传统强度折减法的计算结果进行对比。
1 考虑张拉破坏的强度折减法
1.1 基本原理
τ=c+σntanφ
(1)
式中,c为黏聚力;φ为内摩擦角;τ为剪切面的剪应力;σn为剪切面的正应力。
传统强度折减法基于M-C屈服准则,以岩土体材料的抗剪强度为储备,对黏聚力c和内摩擦角φ进行折减。即
(2)
式中,F为材料的强度折减系数;c′为折减后的黏聚力;φ′为折减后的内摩擦角。
实际上,边坡破坏不只存在剪切破坏,还存在张拉破坏,只考虑剪切破坏不符合实际。根据M-C强度准则,岩土体的最大抗拉强度可通过下式计算
(3)
式中,σtm为材料的最大抗拉强度。传统的强度折减计算由于c和tanφ的折减比例相同,σtm并改变。在实际工程中,岩土体的抗拉强度很难达到最大抗拉强度,将最大抗拉强度折减一次的结果作为实际抗拉强度,即
(4)
式中,σt为材料的实际抗拉强度。
枪声定位模拟实验通过鞭炮声来模拟枪声信号,每次网络检测到枪声信号都存在单一节点直接失效的风险,尤其是簇头的直接失效将会导致整个网络的瘫痪。在一组实验中,存在始终没有作为簇头的节点,并以此节点的实验数据为例,表1中列出了簇头失效情况下的5次检测的结果。序号0表示鞭炮的实际位置,序号1表示单点定位结果,序号2表示本次网络数据融合定位结果。
本文在考虑张拉破坏的基础上,对传统强度折减法进行改进,对实际的抗拉强度再进行一次折减,即
(5)

1.2 失稳方式判别方式的选择
在强度折减法的计算中,边坡失稳判据主要有3类[11]:①塑性区产生贯通;②数值计算在规定次数内未能得到收敛;③边坡特征点(如坡顶、坡脚)的水平位移较上一次计算有明显的突变。郑颖人认为塑性区贯通是边坡失稳的特征,是必要条件而非充分条件。边坡失稳时滑块由静态转为动态,必然会产生很大位移突变,位移突变的判别带有主观性,不宜直接采用。但位移突变时,有限差分法迭代方程的收敛性很难满足,即在计算不收敛的同时也会满足位移突变,所以本文以计算不收敛为失稳判据。
1.3 实现方式
本文基于改进的强度折减法,采用有限差分软件FLAC3D,对黏聚力、内摩擦角和抗拉强度进行折减,流程见图1。建立边坡模型,输入一个较小的数为初始折减系数,对其材料属性进行强度折减并进行有限差分计算,通过计算不收敛判断其是否失稳。如果计算结果稳定,则对折减系数进行递增,回到第二步重新计算,如果计算结果不稳定,输出此时的折减系数为安全系数。

图1 考虑张拉破坏的强度折减法流程
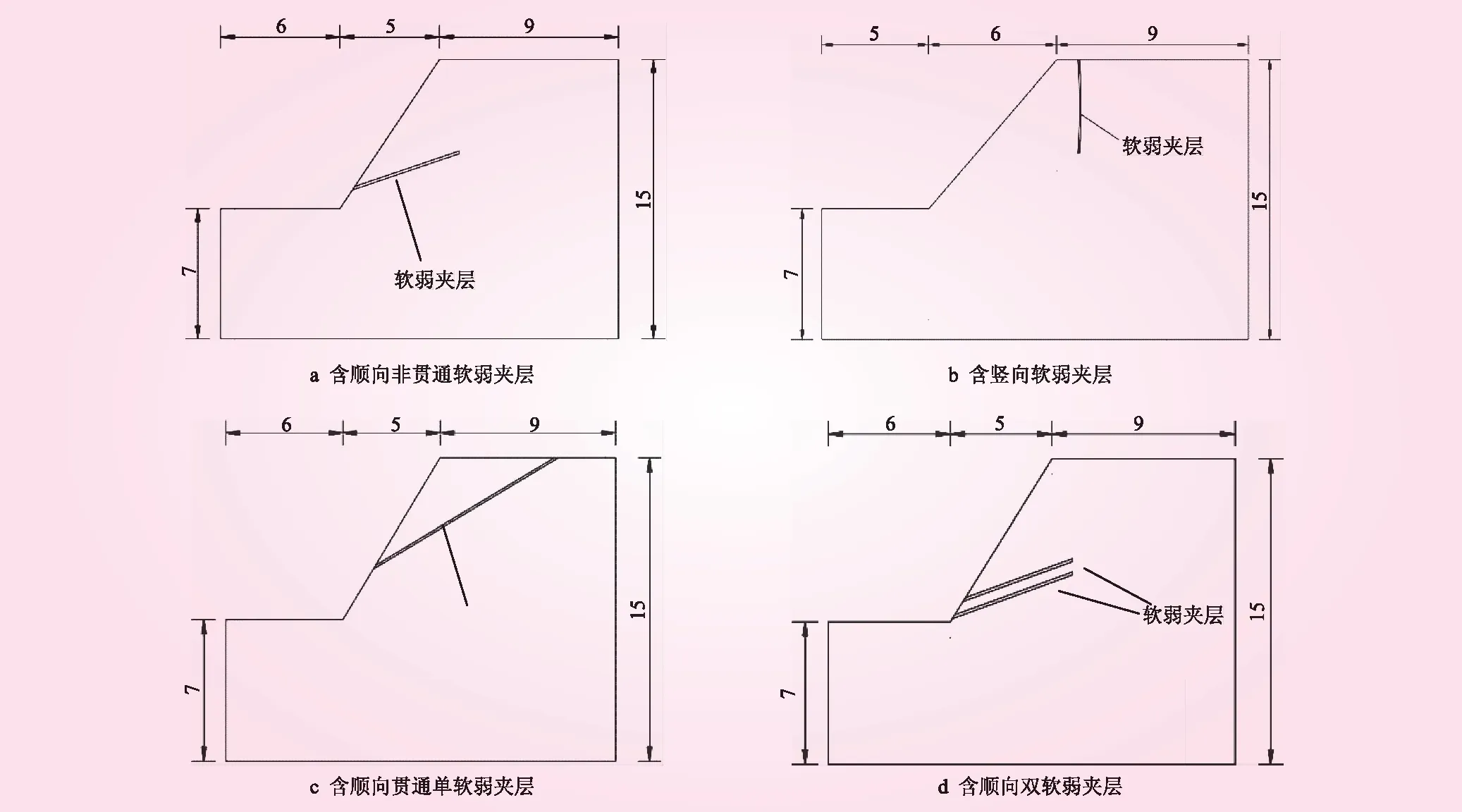
图2 岩质边坡算例(单位:m)
1.4 滑裂面的确定
在有限元强度折减法计算中,临界滑裂面的点往往是沿着深度方向塑性应变最大的点[12],在有限差分强度折减法的计算中,计算结果的塑性区是一片区域,没有塑性应变的数值,所以无法使用剪应变。在FLAC3D中,应变增量是有关节点位移的物理量[13],在一个时间增量步中,四节点四面体单元应变增量的计算公式为
(6)

从式(6)可知,应变增量是一个时间增量步内位移增量的大小,可以认为应变增量为塑性应变。岩土体的破坏大多为剪切破坏,所以将最大剪应变增量最大的位置当做是滑裂面的点是合理的。
2 算 例
本文选取含顺向非贯通软弱夹层岩质边坡、含竖向软弱夹层岩质边坡、含顺向贯通单软弱夹层岩质边坡和含顺向双软弱夹层岩质边坡为典型算例。算例1为坡脚处含顺向非贯通软弱夹层的岩质边坡;算例2为坡顶处含与水平面夹角为90°的非贯通软弱夹层的岩质边坡;算例3为含与水平面夹角为30°的顺向贯通软弱夹层的岩质边坡;算例4为含双顺向非贯通软弱夹层岩质边坡。4种边坡统一采用同等性质的岩体和软弱夹层,岩体的容重γ1=27 kN/m2、黏聚力c1=100 kPa、内摩擦角φ1=30°、弹性模量E1=200 MPa、泊松比ν1=0.3;软弱夹层的容重γ2=20.2 kN/m2、黏聚力c2=50 kPa、内摩擦角φ2=20°、弹性模量E2=50 MPa、泊松比ν2=0.3。岩质边坡算例见图2。
2.1 算例1

图3 本文方法得到的边坡塑性区
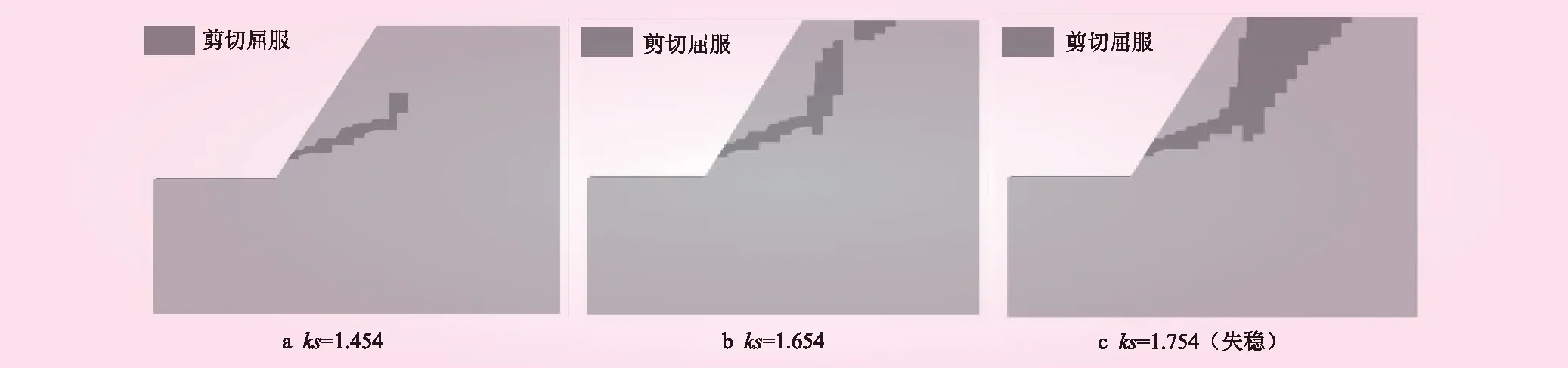
图4 传统方法得到的边坡塑性区
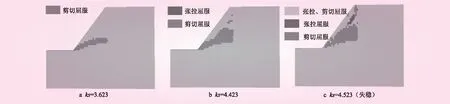
图5 本文方法得到的边坡塑性区
采用考虑张拉破坏的强度折减法计算得到的边坡塑性区见图3。从图3可知,折减系数ks增大到1.365时,底部顺向软弱夹层产生剪切屈服;ks增大到1.565时,剪切屈服区向软弱夹层两侧岩体扩大,并在软弱夹层末端向上发展,同时坡顶开始产生张拉塑性区,并向下发展;ks增大到边坡失稳时,底部剪切屈服区和顶部张拉屈服区贯通,两区域相连并有部分重合。
传统强度折减法计算得到的边坡塑性区见图4。从图4可知,折减系数ks增大到1.454时,坡顶产生剪切塑性区,并向下发展;当折减系数增大到边坡失稳时,底部剪切屈服区和顶部剪切屈服区贯通。
对于这种结构的岩质边坡,2种计算方法的差别主要体现在坡顶的部分区域,考虑张拉破坏时坡顶部分区域为张拉屈服破坏,传统强度折减法计算得到的全部为剪切屈服区。
2.2 算例2
采用考虑张拉破坏的强度折减法计算得到的边坡塑性区见图5。从图5可知,折减系数ks增大到3.623时,坡脚处开始产生剪切屈服,并向后扩展到竖向软弱夹层处;ks增大到4.423时,底部剪切屈服区向上扩展,竖向软弱夹层的底部开始产生剪切和张拉屈服;ks增大到边坡失稳时,后侧软弱夹层全部产生剪切和张拉屈服,并与底部塑性区贯通。
传统强度折减法计算得到的边坡塑性区见图6。从图6可知,折减系数ks增大3.718时,坡脚处开始产生剪切屈服,并向后扩展到竖向软弱夹层底部,同时竖向软弱夹层也产生剪切屈服;ks增大到4.518时,底部剪切屈服区向上扩展;ks增大到边坡失稳时,底部剪切屈服区向上扩展至斜坡处,整个竖向软弱夹层产生剪切屈服。
对于这种结构的岩质边坡,2种计算方法得到的塑性区的范围和形式不同,考虑抗拉强度时后侧软弱夹层产生张拉和剪切屈服,屈服区沿着竖向软弱夹层贯通至坡顶。传统强度折减法计算得到的塑性区全部为剪切塑性区,屈服区沿着两部分向上贯通,一部分贯通至斜坡,另一部分沿着软弱夹层贯通至坡顶。

图6 传统方法得到的边坡塑性区
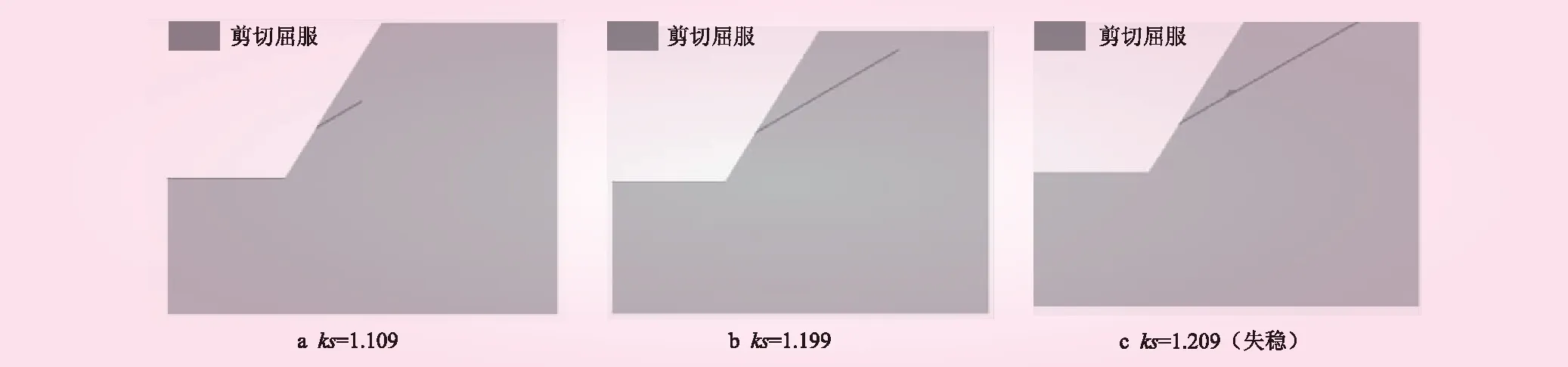
图7 本文方法得到的边坡塑性区

图8 传统方法得到的边坡塑性区
2.3 算例3
采用考虑张拉破坏的强度折减法计算得到的边坡塑性区见图。从图7可知,折减系数ks增大到1.109时,软弱夹层底部开始产生剪切屈服,并沿着软弱夹层向上发展;ks增大到1.199时,软弱夹层范围扩大;ks增大到失稳时,软弱夹层全部产生剪切屈服,塑性区沿着软弱夹层贯通。
采用传统强度折减法计算得到的边坡塑性区见图8。从图8可知,破坏方式与使用考虑张拉破坏的强度折减法的计算结果基本一致。
计算这种结构的岩质边坡,是否考虑抗拉强度,对结果无影响。
2.4 算例4
采用考虑张拉破坏的强度折减法计算得到的边坡塑性区见图9。从图9可知,折减系数ks增大到1.248时,剪切塑性屈服区在软弱夹层处产生,并在软弱夹层末端向上扩展;ks增大到1.448时,剪切屈服区向软弱夹层两侧岩体扩大,并在软弱夹层末端向上发展,同时坡顶开始产生张拉塑性区并向下发展;ks增大到边坡失稳时,底部剪切屈服区和顶部张拉屈服区发生贯通,2个区域相连并有部分重合。
传统强度折减法计算得到的边坡塑性区见图10。从图10可知,折减系数ks增大到1.559时,并且坡顶处也产生剪切屈服,并向下发展;ks增大到边坡失稳时,底部剪切屈服区和顶部剪切屈服区贯通。

图9 本文方法得到的边坡塑性区

图10 传统方法得到的边坡塑性区
对于这种结构的岩质边坡,2种计算方法的差别主要体现在坡顶的部分区域,考虑张拉破坏时坡顶部分区域为张拉屈服破坏,传统强度折减法计算得到的全部为剪切屈服区。
2.5 滑裂面分析
对于上述4种边坡,采用2种方法下计算得到的剪应变增量见图11~14。从图11~14可知,对于算例1、3、4,采用2种方法计算得到的滑裂面差别不大。对于算例2,计算得到滑裂面不同,考虑抗拉强度时,软弱夹层被拉坏并构成了滑块的后缘面;未考虑抗拉强度,在软弱夹层发生剪切破坏前边坡发生失稳,剪切破坏区发展到软弱夹层后,往斜坡方向发展并贯通,后缘面不全是软弱夹层,与实际不符。
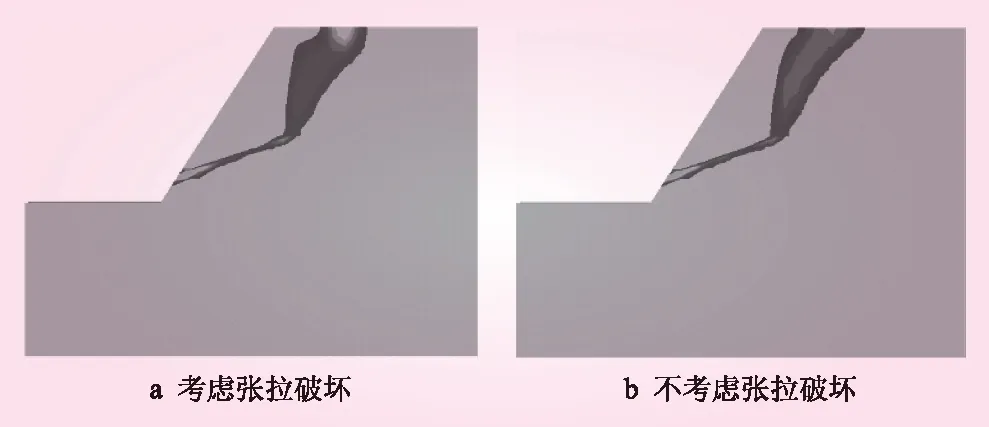
图11 算例1剪应变增量
2.6 结果分析
以上4个算例表明,边坡失稳不只有剪切破坏,还存在着张拉破坏。因此,在采用强度折减法计算边坡时,考虑抗拉强度是合理的,能较好地展示边坡的破坏过程。在边坡失稳过程中,含非贯通顺坡向软弱夹层边坡其破坏特征为剪切破坏;含非贯通竖向软弱夹层边坡破坏特征为部分剪切破坏和部分张拉破坏。但并非所有结构的岩质边坡都存在着张拉破坏,如果存在顺坡向贯通软弱夹层边坡,滑块沿软弱夹层发生剪切破坏。4种典型岩质边坡在2种方法下的计算得到的安全系数见表1。从表1可知,对于算例1、2、4,考虑抗拉强度计算得到的结果更加保守;对算例2,是否考虑抗拉强度不影响计算结果。对比算例1、2,软弱夹层的位置对边坡影响较大,含底部顺向软弱夹层对边坡稳定的影响远大于含后侧竖向软弱夹层。

图12 算例2剪应变增量
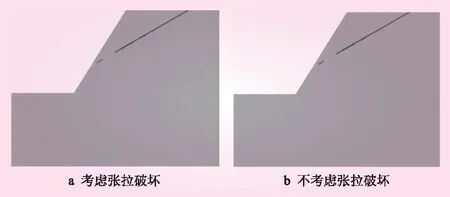
图13 算例3剪应变增量

图14 算例4剪应变增量

表1 不同计算方法各算例的安全系数
3 结 语
本文基于改进的强度折减法,对典型的岩质边坡进行了稳定性研究,得出以下结论:
(1)大部分岩质边坡的破坏区域由张拉破坏区和剪切破坏区组合而成,张拉破坏较多存在于坡顶或竖向软弱夹层中;也有小部分岩质边坡的破坏类型为纯剪切破坏,如含有顺坡向贯通软弱夹层的岩质边坡。
(2)顺向软弱夹层对边坡稳定性影响较大,其主要破坏为剪切破坏;对于竖向软弱夹层,对边坡稳定性影响小于顺向软弱夹层,破坏方式既有剪切破坏又有张拉破坏。
(3)在岩质边坡的数值计算中,考虑张拉破坏得到的计算结果更保守,更加具有工程意义,应当引起设计人员的注意。
