运用模糊层次分析法选择合适的工程项目管理模式

2022-06-22杨国强亳州市重点工程建设管理服务中心安徽亳州236800

砖瓦 2022年6期

杨国强（亳州市重点工程建设管理服务中心，安徽亳州 236800）

项目管理模式选择过程中涉及的条件参数相当复杂，且随着各类建设标准逐步细化，在实现目标控制的过程中，需要多方面更高水平的参与配合。目前，针对工程管理选择和评估模型的建立面临定性和定量两个方面的难题。本文通过模糊层次分析法分析了工程建设过程中的各类因素，根据三角模糊数原则，首先针对标准自身的性质进行分类，而后采用多标准比选的方法，从统计学上评估分类后的项目标准。根据分类结果，本次建立的分析模型处理的分类分为时间（A类）、成本（B类）、工程质量（C类）、施工安全（D类）与风险管理（E类），其中，首项控制因素是A类时间因素，其次为B类成本因素。通过以上工程因素来对工程管理中涉及的各类问题进行成因分解和量化处理，选择出特定的时间、一定成本范围内能稳定高效地完成工程目标并取得客户认可的资源调控和管理方法，对提高工程效率和节省成本有重要意义。

1 工程因素分析与量化

模型建立过程中采用多标准决策的方式对各管理模式进行比选，要实现量化处理，首先需要将所有的因素转化为同一个单元。为了实现条件的数据化和定量化，可以采用质量评估附加不确定性评估参数的方式来简化量化的过程。在简化过程中，采用两两比较的方法对标准进行优先等级排序，从而建立出一个合理的框架。本项目采用成对比较矩阵优化法对模型结构进行调整，采用升序排列程序生成参数的优先级向量，而后进行一致性检验。

1.1 因素分析

工程因素的读取和量化要求工程项目信息完整全面，因素识别是管理模式比选中最基础的环节，这个环节需要将可能影响工程项目进行或者影响工程项目质量的不确定性的因素识别出来，并进行成因的分解。

其中，各类别的因素之间是相互影响的，项目建设过程中的风险和事故大多是各类因素共同作用的结果，因此需要结合项目管理的内容和方式，对各种条件进行分解。为了防止分解过程中重复计算，必须对因素进行维度划分，并严格界定划分标准。

实际工程中，我们一般采用三维或者五维的方式来综合分解项目管理中涉及的各类因素，三维法主要包括时间、目标和政策三个维度，本文采用五维法（见表1），主要包括时间维度、成本维度、目标维度（又称为工程质量维度）、安全维度和风险维度。

表1 各维度所含因素示意表

1.2 量化方法

在传统的层次分析法当中，采用的两两对比的方式为直接系数法，一般系数的来源为专家打分制或者成本-收益讨论制。直接系数的模糊程度较低，对结果的影响过于直观，在定量的数据本就不足的情况下，很难对精确度有一定要求的工程项目做出决策指导。因此，本次模型采用三角模糊数替代直接参数对各因素进行两两对比，见表2、表3。

表2 传统的直接参数标度法

表3 三角模糊数标度法

三角模糊数处理原则是把对目标有影响的内容视为一个连续的函数，将工程中的各类因素视为影响因子，通过以上比较模式赋予各类因素一个模糊数，用表示。͂由三个参数综合构成，参数形式为（m,n,l)，其中m表示重要性比较性成立的最小可能值，l表示重要性成立的最大可能值，n表示判断假设最可能成立的可能值。的计算值如下：

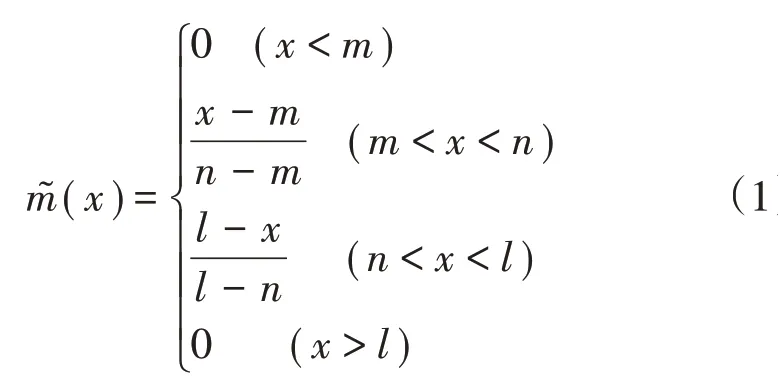
2 层次分析法模型的建立和应用

以安徽某商业建设项目为例，项目于2015年开始建设，2018年投入使用。项目地质检测报告显示其区域内岩层可以对高层建筑的建设提供足够的支撑力，建筑内容包括住宅建设、商业建筑和地下车库。其中，住宅面积为102582m2,商业建筑面积为11310m2，车库（地下一层）建筑面积为2648m2，建筑密度为22.3%，绿化率为48.6%。

2.1 层次结构的建立

对上述工程进行工程因素识别，从上述五个维度包含的管理因素进行分层构建，得到工程管理水平社的分析模型，具体如图1所示。

2.2 分析矩阵的建立

如图1所示，模型的构建分为目标层、准则层和因素层三个层级，每个层级可以用三角模糊数法进行成对比较，从而构建出模糊比较矩阵。

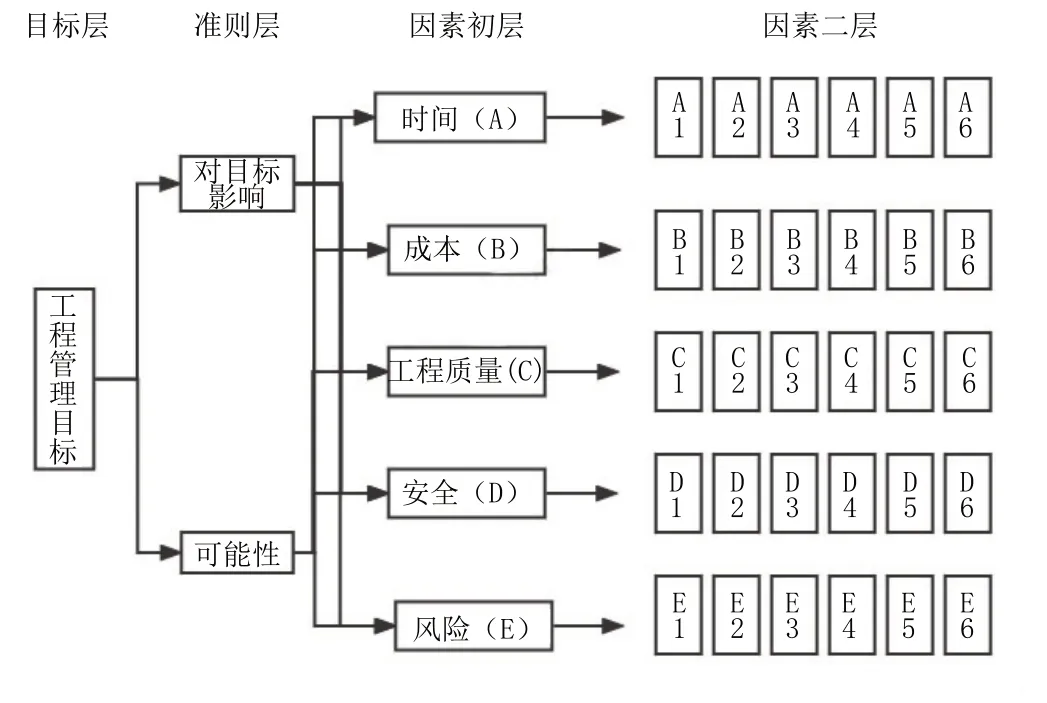
图1 层次分析模型结构图

在进行量化比较的过程中，为了使评估贴合实际情况，最终选取了专家评估制度，由业主方面聘请四位专家和两位资深项目经理从五个维度做出重要性判别，选择众数作为判别结果。以本工程中各因素对目标影响程度的判别为例，判别结果构成的模糊比较矩阵见表4。

表4 三角模糊数比较矩阵

2.3 一致性检测方法

此时，便可以通过归一化排序向量W对矩阵进行一致性检验。本次检验采取常见的相容性指标法则，这种方法能够充分利用已有数据，准确性较好。

相容性指标法需要先计算出W的互补矩阵，而后构建相容性指标函数具体计算公式如下：

一般来说，一致性判断需要事先设置期望值，期望值越小则要求判断的一致性的程度越高。如果不事先指定期望值，多数项目都会采用常规的期望值α=0.1。

通过上述方法我们对矩阵A进行计算机处理，得到相容性装指标值因此可以满足一致性的要求，这说明本次设立的判断矩阵值是合理的，可用于指导判断。

2.4 排序结果

根据计算所得的排序向量，可以体现出计算层（即本例中的因素初层）对上一层中的相关因素（即本例子中准则层中的对目标的影响力因素）的影响比重。对比重大小进行排序，就可以得到单个元素重要性排序矩阵，本例当中的计算与排序结果如图2所示。

图2 单层排序结果示意图

根据排序结果显示，时间是五个维度中对工程结果影响最显著的因素，是工程项目管理过程中需要控制的首要因素。运用同样的流程进行计算，可以得到因素二层的元素对工程时间影响的重要性大小排序，本项目中元素二层对应时间层的因素包括设计、招标、施工、验收、运行五个阶段的工作时间，最终结果显示施工时间对时间因素的影响最大。

成本因素计算排序值为0.285，排在第二位，这表明成本因素同样对目标实现影响较大，需要重点关注。成本因素的下层包含有建材、耗能、劳务、运输、机械损耗五个因素，同样按照构建判断矩阵、验证一致性、计算排序值的流程可以得到本层的判断结果。判断结果显示，与工程管理最相关的因素为建材费用。需要注意的是，本层不包含常见的土地费用，这主要是因为土地费用在项目期间较为稳定且与工程管理模式的选取关系较小，因此不列举在B类因素当中。

3 根据排序结果选择工程管理模式

当前，我国工程项目采用的管理模式主要包括CM模式、Pa-Con模式和CDC模式。其中，CM管理模式依赖第三方单位，采用最短路径法进行施工管理和调节，强调是施工过程中各部门的协调合作，在减少设计变更、节省工程成本、保证工程质量方面具有突出优势。Pa-Con模式是将工程内容明确后统一交接给总负责单位，这种模式的整体性大于其他的管理模式，在降低施工成本方面卓有成效，但是由于内部部分合同的简化和模糊，导致工程风险相对较高。CDC模式是在工程进行之前便设定出清晰投资数和施工时间，同时有明确的阶段规划，但不同的施工阶段可能因为相对独立而容易出现配合不当的问题，因此主要用于强调工期和投资数的项目。

可见，根据上文的排序结果，CDC是最适合于本项目的管理模式。