福建省交通碳排放影响因素与减碳趋势研究

张兰怡，卢秋萍，张园园，戈秋虞，胡喜生，邱荣祖，刘娜翠

(1.福建农林大学 交通与土木工程学院， 福州 350002；2.福建农林大学 计算机与信息学院， 福州 350002)

我国碳排放年均增长率达2.2%，交通运输行业是碳排放主要来源之一,“双碳”目标的提出对交通运输行业的发展带来了巨大挑战[1-3].因此，对交通碳排放进行研究是交通运输业的工作重点，也是交通碳减排政策的制定与施行的首要条件[4-8].

目前，交通碳排放的研究主要从碳排放趋势变化、时空演变规律、交通减排潜力等方面进行[9-10].这些研究的共同点是均需探明研究区域交通碳排放的影响因素，而后根据研究目的进一步深入研究，最终制定相应的减碳策略.不同研究区域的交通情况不同，其碳排放影响因素的选取不尽相同，需要综合内因及外因综合分析.其中，内因指由于交通运输业自身的发展导致交通碳排放量增加，如客、货运周转量上升使能源消耗，导致碳排放量增多；外因指除内因之外的其他原因，如由于经济的发展，人均消费水平提高，使交通运输业相继发展，使交通碳排放量不断增加；此外，人们对出行工具要求不断提高，使机动车保有量逐年增加；城市产业结构的调整和升级，也会对碳排放产生影响[11-12].

福建省交通运输的能耗占全部领域能耗10.1%，由此产生大量的碳排放.因此，在“十四五”发展规划中，福建省把“双碳”目标纳入生态省建设布局，提出交通运输绿色低碳发展策略[13-15].综上，能源需求与交通低碳发展的现状要求对福建省交通碳排放的影响因素进行研究和分析，研究结果可为福建省交通部门制定减排政策提供建议，同时也为其他区域交通碳排放分析提供参考.

1 研究方法与数据来源

1.1 碳排放量测算模型

交通碳排放量测算通常采用IPCC的碳排放系数法[16].该方法分为 “自上而下”测算法和“自下而上”测算法[17-18].对于特定的区域通常采用“自上而下”的碳排放量计算方法，即通过将每一种能源的消耗量乘以能源碳排放系数进行计算.该方法数据获取较容易，故应用较广[19-21].而“自下而上”的测算法主要是基于各运输方式的行车里程进行计算[22-23].考虑到行车里程数据难以获取，基于两种方法的适用范围以及相关数据的可获得性，本文采取“自上而下”法如式(1)：

(1)

其中：C为碳排放总量，单位为104t；i为能源种类；Ei为第i种能源消耗量，燃料油单位为104t，天然气单位为108m3，电力单位为亿kWh；Fi为第i种能源的碳排放系数，见表1.

表1 主要能源的碳排放系数Table 1 Carbon emission coefficients of major energy sources

注：天然气系数单位为kg·m-3，电力系数单位为kg·(kW·h)-1，其他能源系数单位为t·t-1.

数据来源：《综合能耗计算通则》与《省级温室气体清单编制指南》中低位发热量，折煤标准系数以及碳氧化率计算结果.

1.2 碳排放强度测算模型

碳排放强度用于确定交通发展水平与社会及经济发展关系的重要指标，碳排放强度越低，说明在同一GDP水平下，碳排放量越少.碳排放强度测算模型如式(2)：

(2)

其中：CI为碳排放强度，单位为t/万元；C为碳排放总量，单位为104t；G为国民经济生产总值，单位为亿元.

1.3 扩展STIRPAT模型

STIRPAT模型是综合考虑人口、经济和技术等因素的模型，是一种包含随机项的多元线性回归模型[24]，公式如下:

I=aPbAcTde

(3)

其中：I为环境影响因素；P为人口总数；A为经济发展水平；T为技术发展水平；e为随机误差；b、c、d分别为模型参数对应指数.

本文从内因与外因两个方向进行研究.内因选择客运周转量(Turnover Volume of Passenger Traffic,TP)、货运周转量(Turnover Volume of Goods,TG).外因包括碳排放强度(Carbon Intensity,CI)、人均GDP(Per Capita GDP,PG)、机动车保有量(Vehicle Ownership,VO)和城市化率(Urbanization Rate,UR).扩展后的STIRPAT模型公式如式(4)：

C=a×TPβ1×TGβ2×PGβ3×VOβ4×CIβ5×URβ6

(4)

其中：C为交通碳排放总量，单位为104t，对应式(3)中的环境因素I；TP为旅客周转量，单位为亿人km，对应式(3)中的人口项P；TG为货物周转量，单位为108tkm，对应式(3)中的人口项P；PG为人均GDP，单位为万元，对应式(3)中的经济水平A；VO为机动车保有量，单位为万辆，对应式(3)中的经济水平A；CI为碳排放强度，单位为t/万元，对应式(3)中的技术T；UR为城市化率，单位为%，反映区域环境特点.

对式(4)两边分别取对数，可得:

lnC=lna+β1lnTP+β2lnTG+β3lnPG+

β4lnVO+β5lnCI+β6lnUR

(5)

其中：β1、β2、……、β6分别为上述变量回归系数，表示当影响因素TP、TG、PG、VO、CI、UR发生1%的变化时，将分别引起碳排放C发生β1%、β2%、……、β6%的变化.

1.4 支持向量回归模型

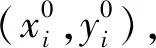
1)对所有样本数据进行归一化处理.

(6)

2)将样本数据随机分为训练集和测试集.选择核函数处理训练集，惩罚参数c和核函数g的取值由网格搜索法确定，得到预测模型最优参数为ε*、c*、g*.

3)对训练集进行数值训练，得到最优参数ε*、c*、g*和回归函数f(x).将数据输入到回归函数中，得到模型的预测值；之后将预测值与实际值进行回归，根据回归方程的相关系数及均方根误差来验证模型的精度.

4)将数据进行归一化，代入回归函数.进行反归一化处理后得到预测值.

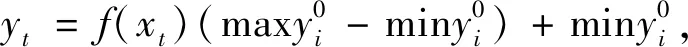
i=1,2,…,n

(7)

1.5 主成分分析法

由于交通碳排放影响因素较多，为了区分影响因素的贡献率，采用主成分分析法对其进行降维，得到贡献率程度大的指标作为主成分，模型相关描述见本团队前期研究论文[25].

1.6 数据来源

研究所需的客、货运周转量、机动车保有量、人均GDP数据来源于《中国区域经济统计年鉴》、《中国统计年鉴》；城市化率数据来源于《福建省统计年鉴》；CO2排放量以及碳排放强度数值根据式(1)与式(2)基于《中国能源统计年鉴》中煤炭、焦炭、汽油、煤油、柴油、燃料油、天然气以及电力数据计算而来的.相关数据见表2.

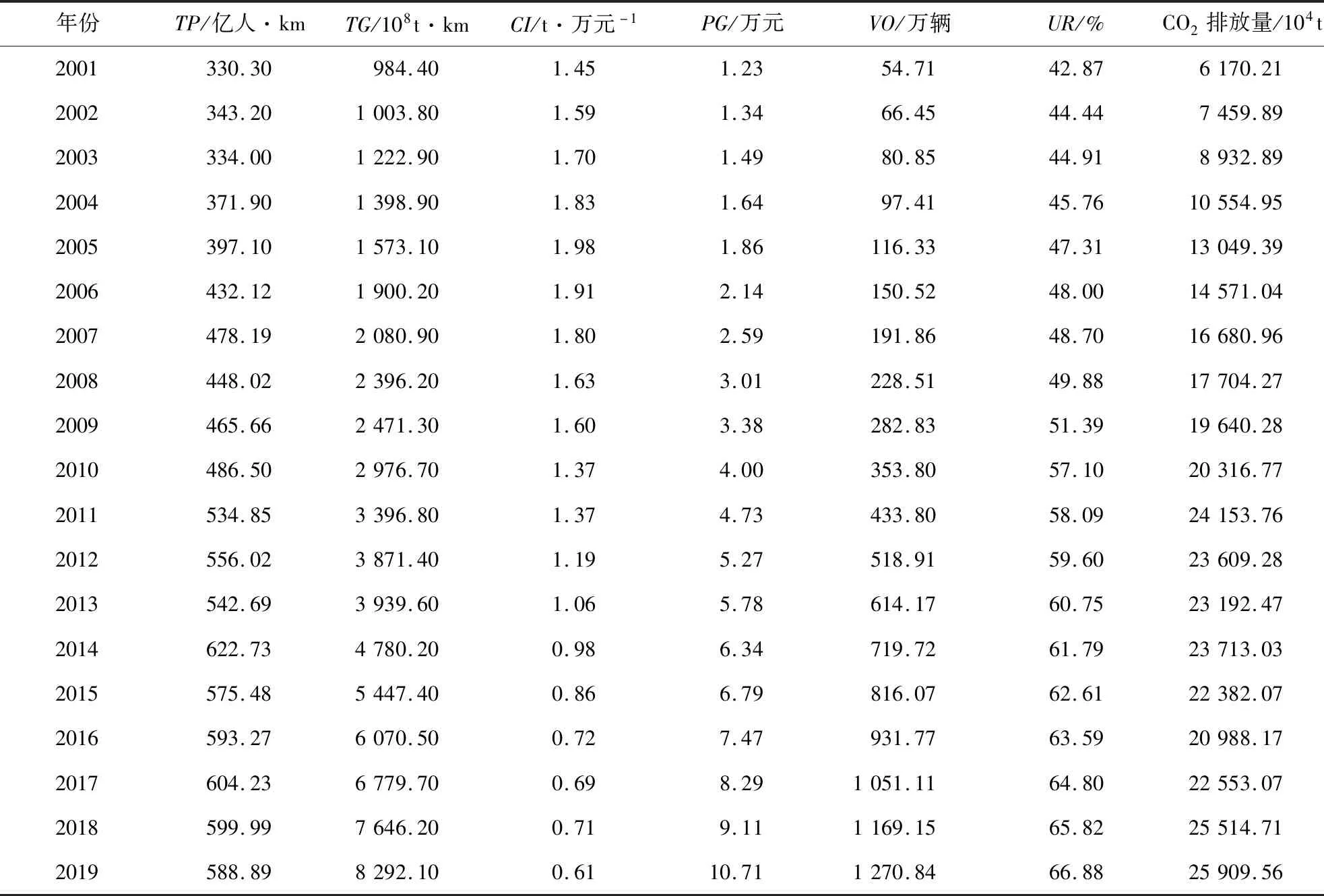
表2 福建省交通碳排放及其影响因素数据Table 2 Transportation carbon emission and its influencing factors data of Fujian Province

2 交通碳排放影响因素预测

2.1 最小二乘回归分析结果

基于最小二乘回归的结果见表3，F值为111 026.49，对应的显著性水平为0.000，说明模型具有显著相关性；R2及调整R方都为0.999 9，说明模型拟合度较高.模型中的TP和VO指标系数为负，并且其中CI指标系数为正，与实际不符；且模型的t检验结果不理想，说明普通最小二乘回归系数不显著；参数TP、TG、PG、VO、UR的VIF值分别为32.834、167.819、468.188、667.144和76.77全部大于10，说明回归模型存在多重共线性问题.因此，本文采用岭回归法解决上述问题.

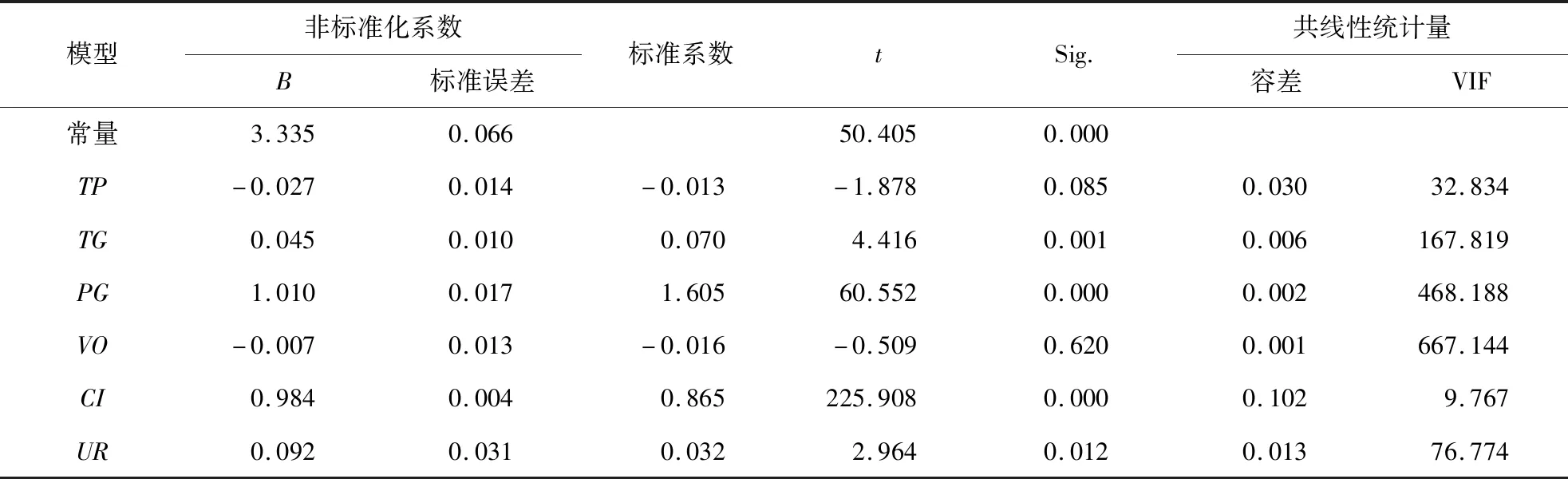
表3 普通最小二乘回归结果Table 3 Ordinary Least Squares Regression Results

2.2 岭回归分析结果

设定岭参数K的范围为(0,1)，数据间隔为0.01.TPK、TGK、PGK、VOK、CIK、URK等分别表示各回归系数的岭参数K值.从图1中可以看出，当K=0.2时，岭参数变化趋于平稳，因此选择参数K为0.2.此时模型R2和调整R2分别为0.95和0.92，接近于1，p值为0.000 000 62，远小于0.01，说明回归方程的显著性较好.结果表明：当福建省TP、TG、PG、VO、CI、UR各自变化1%时，将分别引起交通碳排放量0.627%，0.125%，0.14%，0.103%，0.346%，0.516%的变化.自改革开放以来，福建省在区域经济发展上提出了一系列的发展布局，使得福建省城市化率越来越高，人均GDP增加，机动车保有量增多，社会范围内的客货运需求不断增加，促进了福建省经济的高速发展，但随之而来的是环境问题，交通碳排放就是问题之一，因此，治理交通碳排放的前提需要明确福建省交通碳排放影响因素的量及变化趋势.

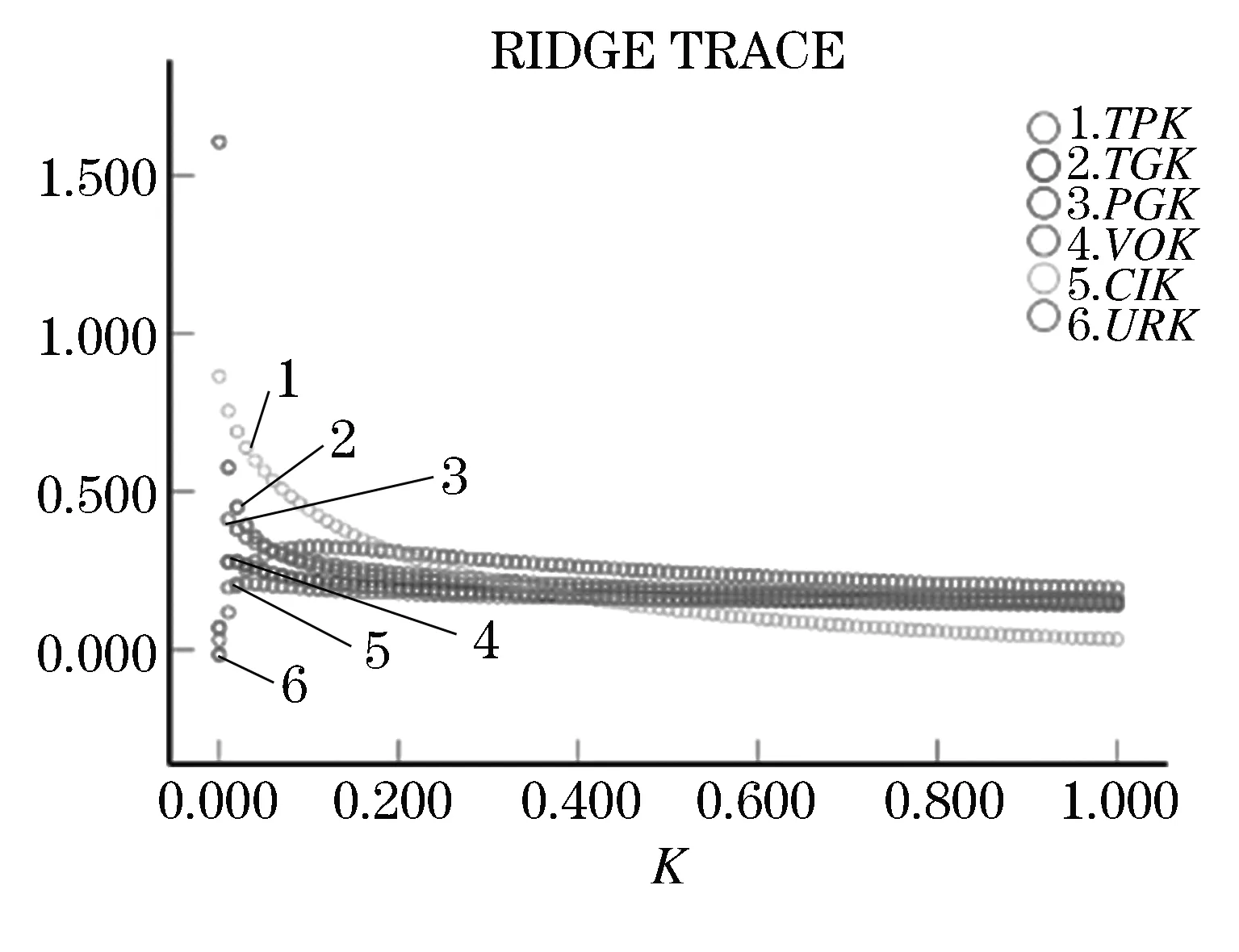
图1 岭迹图Figure 1 Ridge trace map

2.3 支持向量机回归模型结果

从表2随机选取10 a数据组成训练集，余下9 a的数据组成测试集.设置模型的初始值为0.01，采用网格搜索算法及交叉验证法对惩罚参数c和核函数g进行寻优，设置c和g的取值范围均是[2-8,28]，网格宽度为0.2.最终得到模型最佳惩罚参数及核函数对(c,g)值为(222.86, 0.0103)，并且模型最优参数对选择的交叉验证均方根误差仅为0.03.参数选择三维效果如图2所示，其中X轴与Y轴组成的平面图为参数对(c,g)经过离散化之后的参数选择效果图，X轴和Y轴分别为惩罚参数c和核函数g的对数取值，Z轴为归一化数据之后的交叉验证均方根误差值.分别对训练集及测试集数据进行拟合，得到回归结果及对比结果见图3.训练集的回归结果相关系数为0.98，均方根误差为0.008，测试集的回归结果相关系数为0.97，均方根误差为0.01，验证了预测模型的有效性.

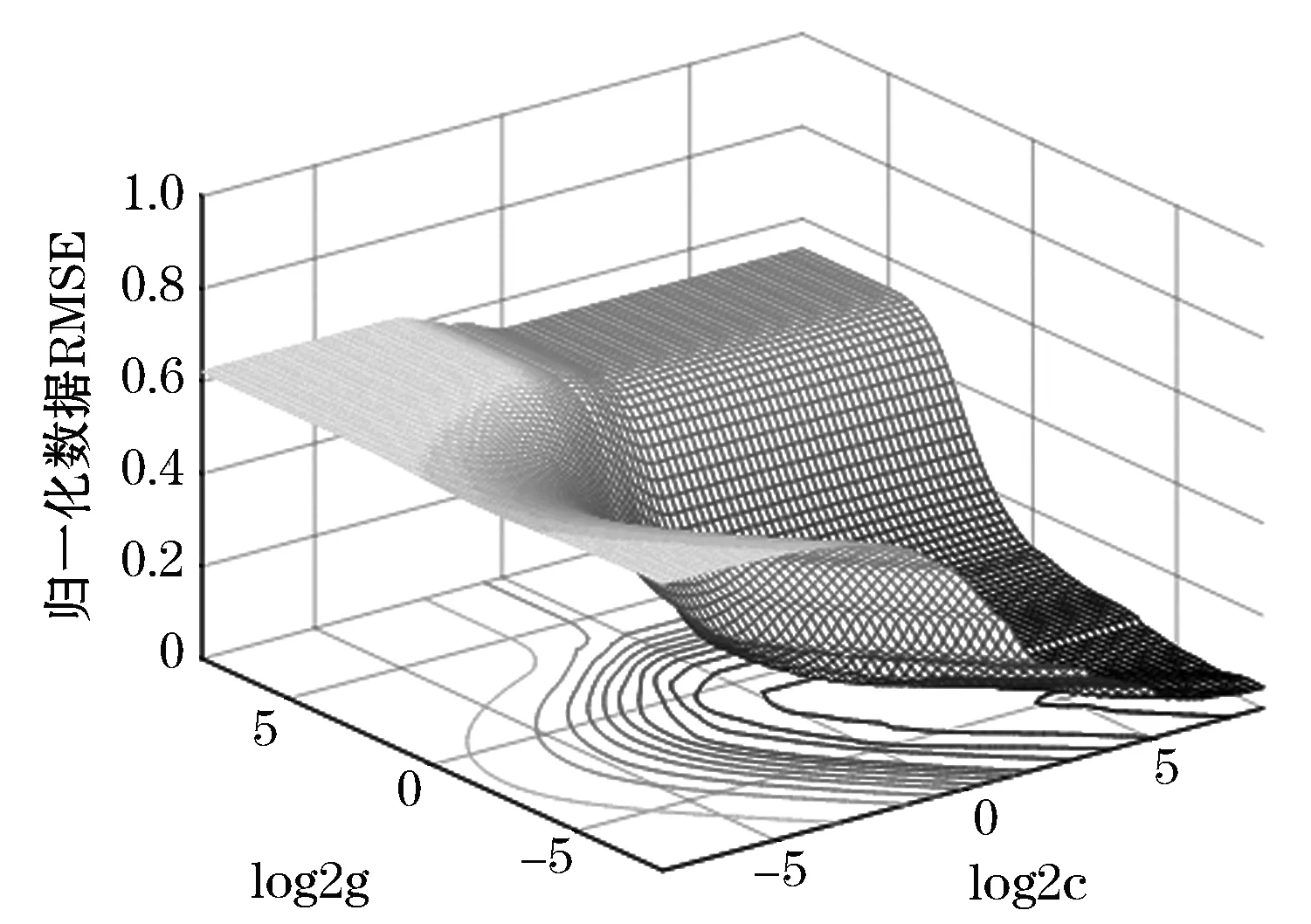
图2 参数选择效果图Figure 2 Effect of Parameter Selection

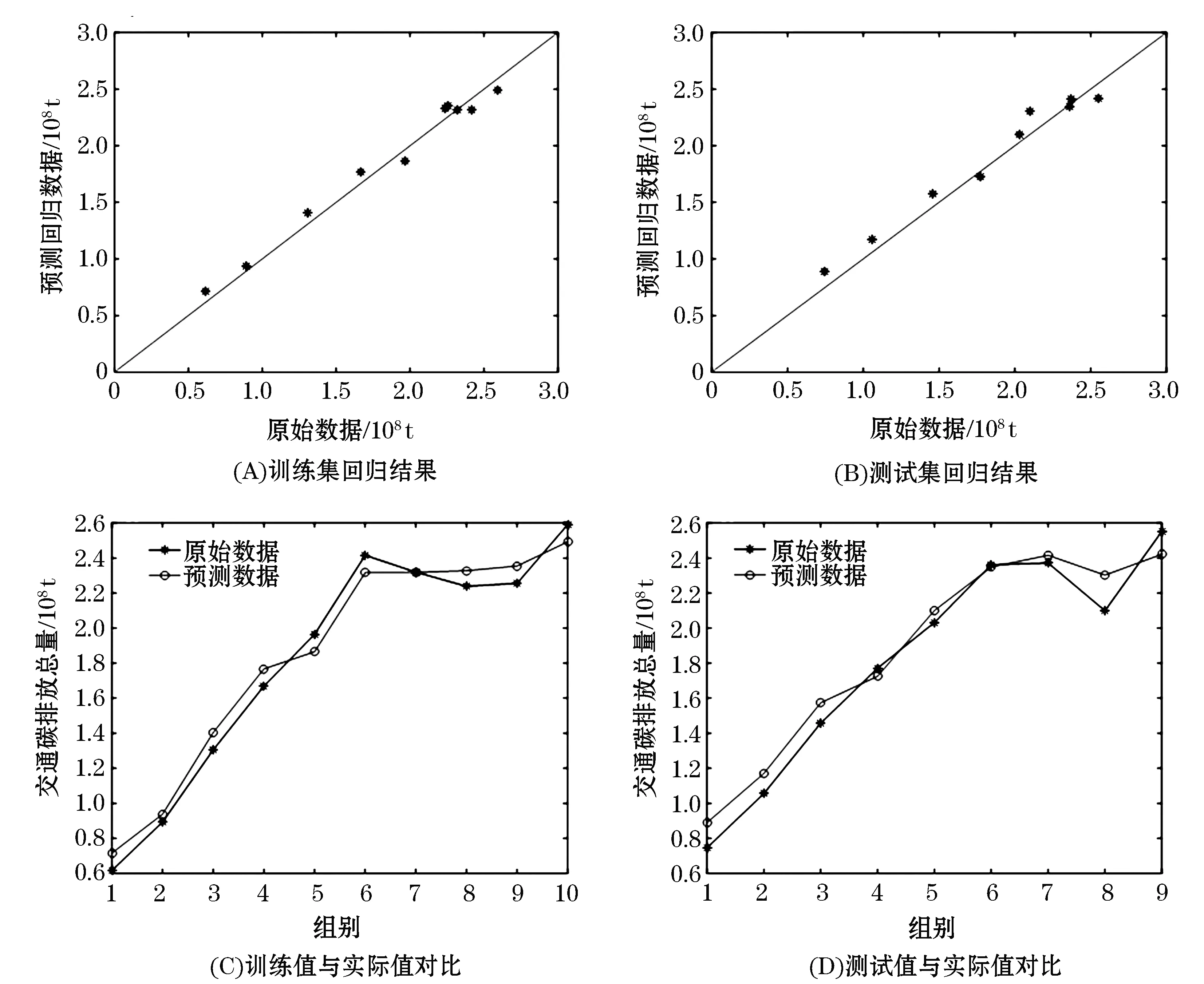
图3 支持向量机回归模型结果Figure 3 Support vector machine regression model results

2.4 交通碳排放影响因素预测

2.4.1 交通碳排放影响因素年均增长率设置

1)TP、TG

2019年福建省客、货物周转量分别为588.89亿人km和8292.13 108t·km，年均增长率分别为3.1%和11.8%.因此，设置TP、TG年均增长率不变.

2)PG

2019年福建省全省生产总值4.23万，增速为8%.根据福建省经济发展政策的要求，未来福建经济社会发展的主要目标是全省GDP同比增长7%～7.5%.因此，综合考虑福建省发展现状，设置PG年均增长率为7%.

3)VO

2009～2019年机动车保有量年增长率为8.7%～29%，呈现逐年递减的趋势，2019年福建省机动车保有量增长率仅8.7%.因此，将VO年均增长率设置为8%.

4)CI

考虑“双碳”目标及福建生态省定位，设置福建省交通CI年均降低速率为7.9%.

5)UR

2019年福建省城市化率为66.88%，样本数据的年均增长率为2.36%，因此，设置UR年均增长率不变.

2.4.2 交通碳排放影响因素预测结果

根据2.4.1所设，得到各个影响因素在2020～2025年的预测值，结果如图4所示，除了碳排放强度呈现逐年递减趋势外，其余影响因素均表现为逐年增加.

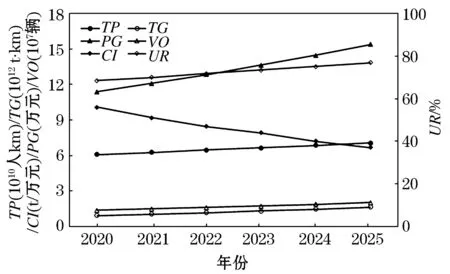
图4 影响因素预测结果Figure 4 Influencing factors predicting results

3 福建省交通碳减排潜力分析

3.1 基于主成分分析的交通碳排放影响因素分析

为了探明各影响因素的贡献度，将TP、TG、CI、PG、VO、UR等6个指标采用主成分分析法进行分析.将所有指标标准化，根据特征值大于1和碎石图结果，提取到1个主成分，累计贡献率为94.657%(表4、图5).根据成分得分系数矩阵结果TP、TG、CI、PG、VO和UR的主成分值分别为0.936、0.986、-0.949、0.993、0.990和0.982.因此，确认主成分因子为PG，说明其能较好地反映交通碳排放趋势，可替代原6个指标进行研究.

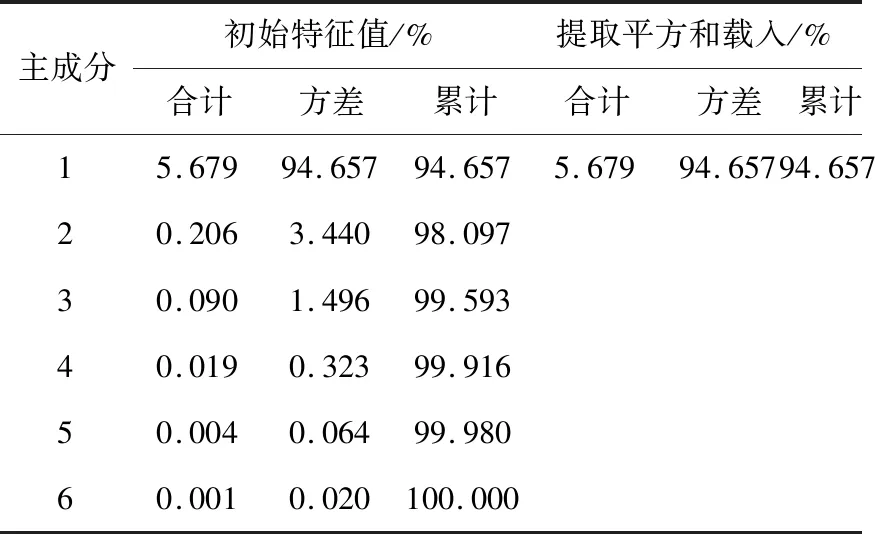
表4 解释的总方差Table 4 Total variance of the explanation

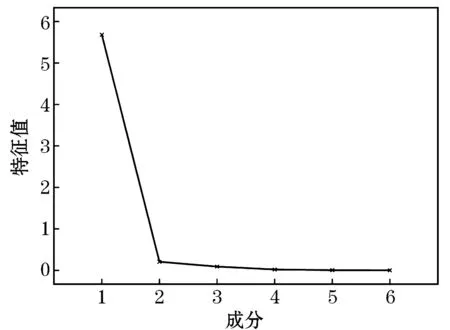
图5 碎石图Figure 5 Scree plot

3.2 基于PG的交通减碳潜力分析

根据福建省经济发展目标，将PG年均增长率分别设置为7%、7.5%、8%.以上节所得数据为基础数据，利用SVR模型预测基于不同PG增长率的交通减碳趋势，结果如图6所示.可知，不论在何种经济增长率下，2020～2025年福建省交通碳排放量均呈现递减的趋势.但随着PG增长率的提高，交通碳排放量也越高，说明经济发展和交通碳排量存在正相关的关系.

图6 不同PG增长率下福建省交通碳排放预测Figure 6 Prediction of transportation carbon emissions in Fujian Province under different PG growth rates

4 结 语

本研究对福建省交通碳排放影响因素进行分析和预测，利用主成分分析法确定影响因素的主成分，并基于支持向量机模型得到不同人均GDP增长率下福建省碳排放量，从而得到不同人均GDP增长率下福建省碳减排趋势，研究结果可为政府在制定城市经济发展与交通减碳政策时提供理论参考.

本研究仍存在不足之处，如在对影响因素进行研究时，未考虑影响因素之间的相互作用机理；且未从动态化的角度考虑影响因素未来的发展情况.未来在区域交通碳排放影响因素及其动态发展趋势方面需要进一步深入、细化.