云南会泽井水位对2014年鲁甸MS6.5地震同震响应过程模拟*

魏海滨，谷洪彪，孔慧敏，3，迟宝明，3

(1.防灾科技学院，河北 三河 065201；2.河北省地震动力重点实验室，河北 三河 065201；3.中国地震局工程力学研究所，黑龙江 哈尔滨 150006)

0 引言

井水位的同震变化反映了脆性地壳受到地震的影响，导致含水层介质的应力状态发生改变，使井水位呈现出阶跃、振荡或持续性变化。地震时井水位表现出的不同响应方式表明其物理机制复杂且影响因素较多，如井震距、含水层特性及井孔结构等。静态应变理论及含水层固结理论对井水位同震阶跃变化进行了合理解释(Wakita，1975；Roeloffs，1996；Quilty，Roeloffs，1997；Grecksch，Roth，1999；Jónsson，2003；Itaba，2008；Wang，2009；Wang，Manga，2009)；地震波通过时造成含水层中裂隙的开合、裂隙中胶体颗粒的堵塞与疏通或是孔隙中气泡的迁移等导致含水层的渗透性发生变化，可能是造成井水位同震振荡与持续性变化的原因(Roeloffs，Evelyn，1998；Elkhoury，2011；Manga，2012；史浙明，2015)。地震造成的静态应力与峰值动态应力均会对井水位变幅产生影响，Ge和Stover(2000)认为与孔压扩散时间尺度相比地震波引起的动态应力会在含水层中迅速衰减，且在地震波通过后含水层一般不会产生永久应变，故本文忽略动态应力的影响，主要关注同震静态应力引起的含水层与井孔水动力响应过程。

利用静态应变理论研究近场井水位的同震响应，涉及不同的时间与空间尺度，是一个复杂的三维流固耦合过程，该过程利用解析法求解具有极大的挑战性。数值模拟是目前研究地震水动力学问题的重要手段，数值模拟过程中利用多种软件的耦合计算来描述同震水位响应过程已有一些成功案例(Ge，Stover，2000；李悦，2011；Nespoli，2016；Zhang，2020；Lei，2021)。然而，近场同震水位响应过程物理机制复杂、影响因素众多，利用数值模拟方法模拟近场同震水位响应仍存在一些问题。首先，这些数值模拟模型均未考虑井-含水层系统内地下水由孔隙或裂隙介质中的流动变为井孔中纯流体域中的流动这一过程，其次已有研究仅使用简单的孔压扩散方程对研究区震后孔压恢复过程进行模拟，未考虑流固耦合过程。

针对上述问题，本文基于Okada位错理论计算2014年鲁甸6.5地震同震静态应变场分布，建立应力场-渗流场耦合控制方程组，以鲁甸地震同震静态应变场为初始条件，模拟鲁甸地区(200×200)km孔压的响应及恢复过程，最后利用达西定律与Navier-Stokes方程将含水层内孔压扰动值转化为会泽井孔内水位变幅值。本文在一定程度上还原会泽井水位对鲁甸地震的同震响应过程，分析近场地震活动与井水位变化之间的关系，为其它近场地震引发的井水位变化研究提供思路借鉴，也为今后探索更为复杂的流-固-热-化学多物理场耦合井水位同震响应的模拟方法提供参考。

1 鲁甸地震及会泽井水位概况

1.1 鲁甸地震发震构造

2014年8月3日16时30分云南鲁甸龙头山镇发生6.5强震，震中位置(27.11°N，103.35°E)，震源深度12 km。本次地震发生在巴颜喀拉块体、川滇块体和华南块体交汇区南部，马边断裂南段、昭通断裂、莲峰断裂之间。由于本次地震造成的断层破裂长度有限且未达到地表，因此破裂面方位不易识别。震后许多学者及机构通过地震烈度分布和地震破裂过程反演对鲁甸地震的发震断层进行了研究，得出鲁甸地震发震构造为一条新发现的近北西走向的断层——包谷垴—小河断裂(房立华等，2014；李西等，2014；徐锡伟等，2014；李艳娥等，2015)。但又有学者通过视震源时间函数分析、余震分布及震源机制解研究提出鲁甸地震可能是由近东西向和近南北向的共轭断层先后破裂导致(张勇等，2015)。

本文研究参照中国地震局对于鲁甸地震的初步分析报告(Cheng，2015)，鲁甸地震为一次高倾角左旋走滑地震，发震断层为走向340°的包谷垴—小河断裂(图1)。

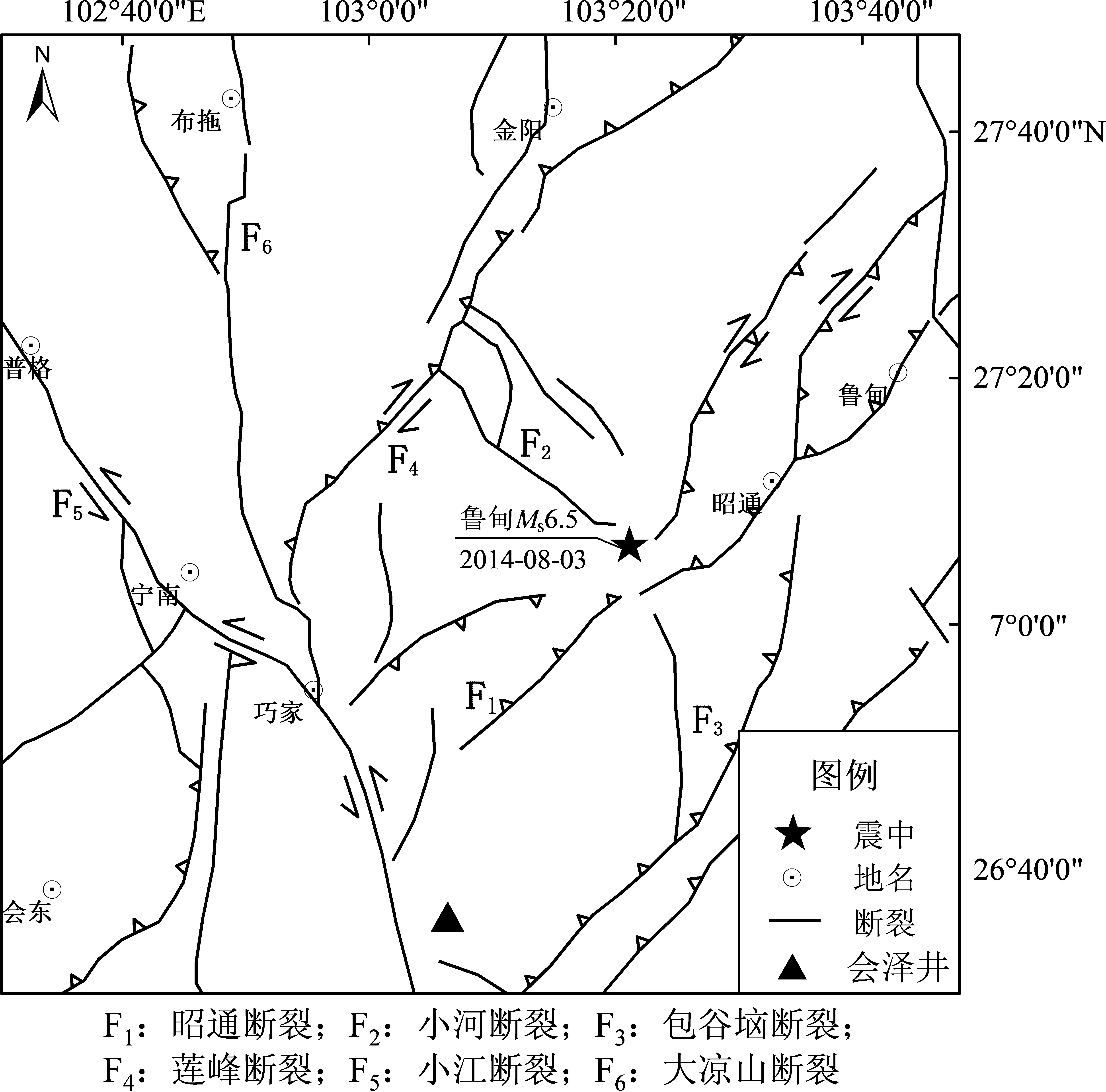
图1 鲁甸地震震中及其附近地区发震构造图

1.2 会泽井水位观测

云南会泽井(滇01号井)为静水位观测井，地理坐标为(26.52°N，103.15°E)。井孔地处川滇地块东南部，位于小江、莲峰、则木河3大断裂的交汇部位，构造位置特殊，井孔周边水文地质条件如图2a所示。会泽井受白雾街不对称双曲弧形构造控制，张性裂隙发育，为地下水的富集提供了有利条件，井孔周边致密玄武岩柱状节理发育，易于形成地下水的运移通道，加上两侧岩溶水的侧向补给以及大气降水的天然补给，使得井孔所处含水层具有较好的补、径、排条件，能够形成一定规模的含水系统。会泽井深103.15 m，井孔半径54 mm，套管深度87.8 m，水位埋深约30 m，滤水管为34.06～87.80 m，观测段为34.06～103.15 m，观测层岩性主要为第四系风化玄武岩(图2b)，地下水类型为裂隙承压水，水温约16 ℃(Sun，2019)。

会泽井自2012年开始数字化观测，水位对其周边几次地震均有响应，映震性较好(图3a)。多年来，水位整体呈缓慢降低型，水位下降速率约为0.3 m/a，大气降水对水位影响较小，气压效应不明显，有固体潮效应。在2014年鲁甸6.5地震时，距离震中约70 km的会泽井水位有同震响应，水位在地震发生时瞬时上升0.33 m，之后开始下降，并在震后50 d内逐步恢复至震前水平(图3b)。

图3 2012—2014年会泽井水位变化(a)和2014年鲁甸MS6.5地震会泽井水位的同震响应(b)

2 鲁甸地震同震静态应变场

假设地震造成井水位的变化是由地震静态应变场导致基质骨架变形产生的应力，从岩石向孔隙流体传递引起的。本文采用美国地质调查局(USGS)开发的Coulomb 3.3软件，利用Okada(1992)有限矩形源模型对鲁甸地震造成的同震静态应变场进行计算，参数选取见表1，得到2014年鲁甸6.5地震同震静态应变场等值线图(图4)。由图4可见，红色区域应变值为正值，属于拉张区域，蓝色区域应变值为负值，属于压缩区域。应变拉张与压缩区域呈现四象限分布，极值分布在断裂的两侧，量级为10，远离断层应变逐渐减小。

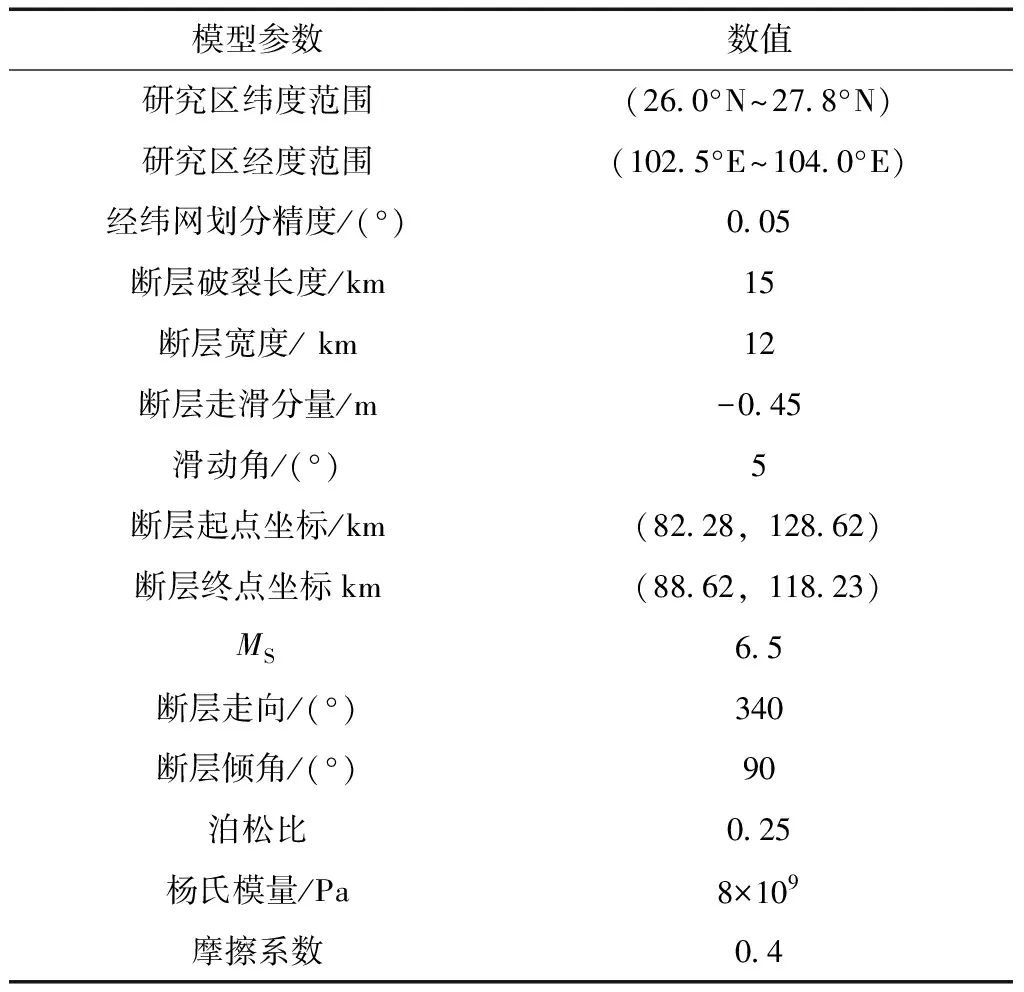
表1 同震静态应变场计算参数

图4 2014年鲁甸MS6.5地震同震静态应变场分布(断裂名称同图1)

3 井水位同震响应数值模拟

地震造成地壳产生形变，使得含水层骨架应力向孔隙中的流体传递，导致含水层中孔压受到扰动并在压力梯度的驱动下扩散恢复，造成地下水从井孔流入或流出，最终反映为井水位的变化。水位同震响应主要包括地震造成的静态应变场分布、含水层孔压扰动及扩散、压力扰动下井-含水层系统水位响应3个部分。

3.1 含水层孔压扰动及扩散数学模型

含水层中孔压受地震静态应力的影响，在压力梯度的驱动下扩散恢复，这个过程中含水层的弹性变形和孔隙水压的扩散是一个流固耦合的过程，因此，需要建立含水层应变与孔压之间的耦合数学模型来定量解释二者之间的关系。本文对含水层孔压扰动及扩散控制方程的建立和求解作如下假设：①含水层为均质各向同性、连续的承压含水层，顶、底板水平；②多孔介质骨架为各向同性弹性体，骨架变形为小变形，符合线性孔弹性理论；③地下水流符合达西定律；④地下水流为等温渗流；⑤渗透率各向同性；⑥单元体内流体无外部源汇项。

本文只关注静态应力对含水层孔压的扰动，忽略加速度的影响，在含水层中选取典型单元体并进行受力分析。利用静力平衡方程、广义胡克定律、有效应力原理、达西定律与质量守恒定律，建立含水层中任一单元体在受到静态应力作用下应变与孔压的耦合控制方程组，具体推导过程见魏海滨(2021)的研究：

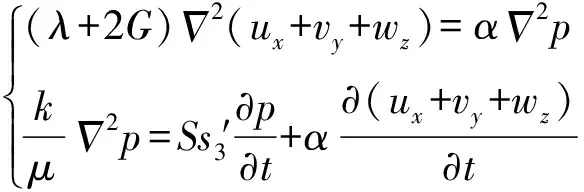
(1)

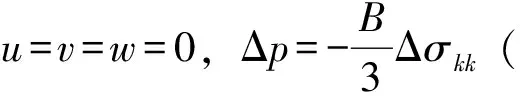
图5 含水层孔压扰动及扩散模型范围及震中、井孔分布图

3.2 压力扰动下井-含水层系统水位响应数学模型

在井-含水层系统中，当地下水在压力梯度的驱动下由含水层向井中流动时，水流方向由纵向变为垂向，且井中为纯流体域。因此，地下水在井中的运动有别于水流在含水层中的运动，在井-含水层系统中孔隙水压扰动从压力扰动源到井中水位变幅，应分为含水层中压力扩散与井中水柱运动两部分。为了刻画在静态应力的影响下孔压在含水层中扩散并在井中以水柱的形式运动这一过程，本文建立了以井为中心的二维轴对称的小尺度模型(图6a)。

该模型包含承压含水层与井两部分，井孔半径54 mm，含水层概化为厚100 m、半径100 m。在侧边界施加地震静态应力导致的孔压变化值，边界处孔压变化值的作用使得含水层内产生孔压梯度。在孔压梯度的驱动下，含水层中的水流向井或井水中流向含水层运动(井孔只在侧壁进水流速为)(图6b)。当地下水在承压含水层中运动时，假设含水层均质各向同性，顶、底板水平，水流符合达西定律：

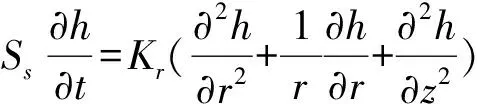
(2)

式中：为贮水率；为径向渗透系数。

当地下水进入井孔后，水流由径向流动变为垂向流动，且井孔为纯流体域，故采用Navier-Stokes方程描述井孔中水流的运动：

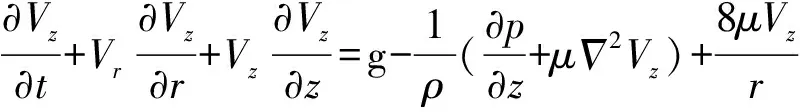
(3)

式中：为井孔中水流速度；g为重力加速度；为孔压；和分别为水的密度和动力粘滞系数。

在初始时刻，含水层中各点孔压为静水压力，即=g；边界条件为：=g+Δ。

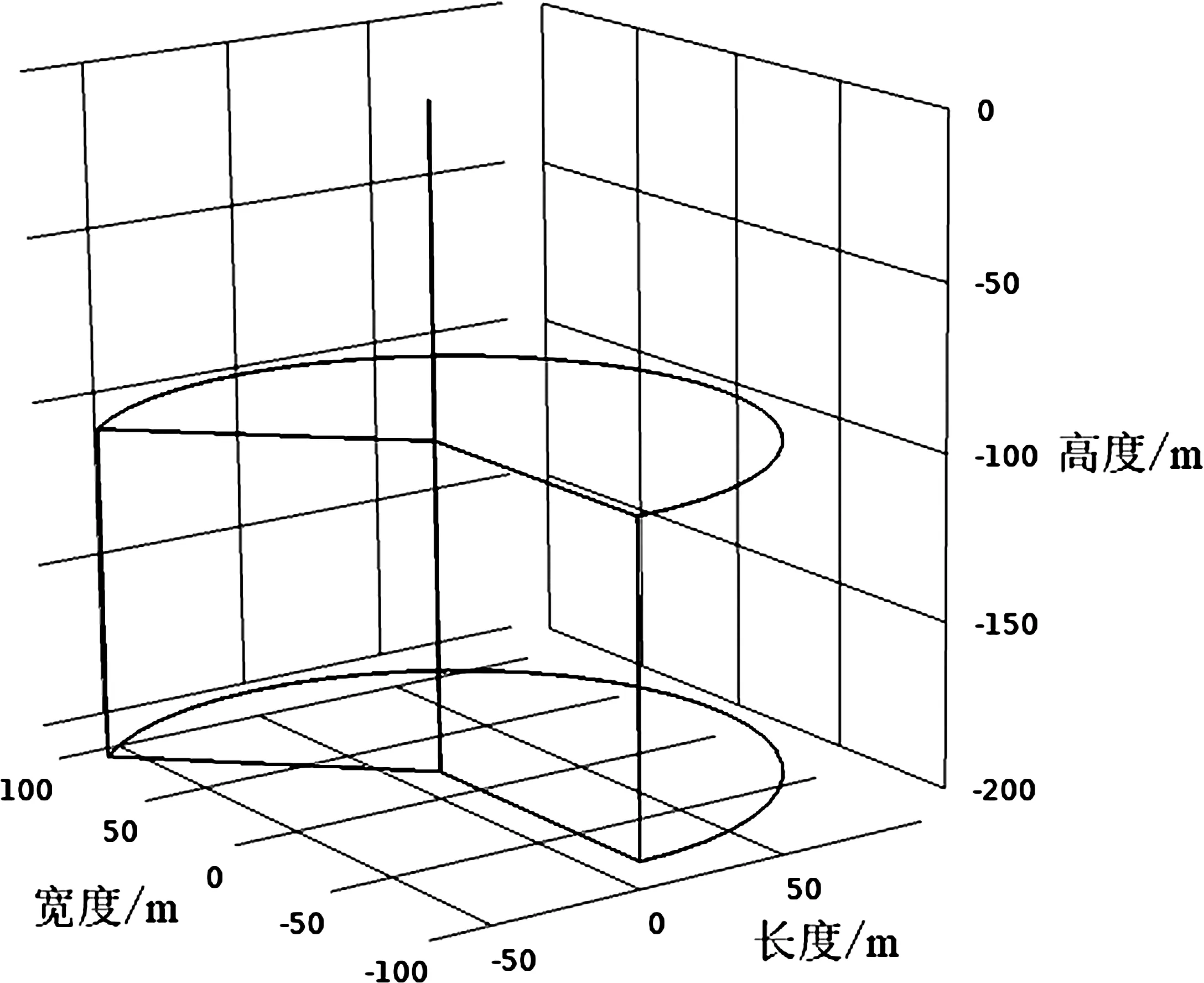
(a)压力扰动下含水层-井系统水位响应二维轴对称模型图

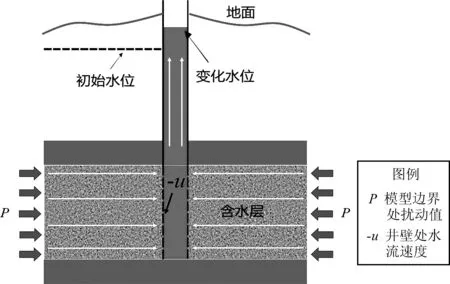
(b)模拟水位同震变化过程示意图

3.3 数值模拟过程

将鲁甸地震静态应变场转化为含水层孔压扰动值，以此作为初始条件，利用COMSOL Multiphysics中的PDE模块，在200 km×200 km×0.5 km的研究区范围内对建立的含水层孔压扰动及扩散数学模型进行求解，获得研究区0.1 km深度处含水层孔压演化规律。最后，在COMSOL中利用内置的达西定律、层流模块，建立以井孔为中心、半径100 m的小尺度井-含水层系统模型，以静水压强为初始条件，利用含水层孔压扰动及扩散模型中会泽井孔所处剖分网格的平均孔压扰动值作为边界条件，对会泽井水位的变化趋势进行模拟。

3.3.1 含水层孔压扰动及扩散数值模拟

基于研究区概念模型(图5)构建三维几何模型用于数值模拟，将式(1)表示为广义矩阵形式，输入COMSOL Multiphysics的PDE模块：

(4)

其中，

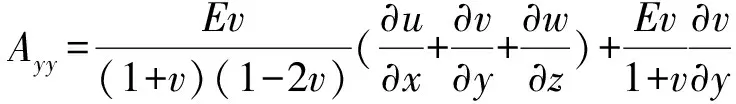
研究区浅层含水层岩性主要为二叠系峨眉山组风化玄武岩，本文利用等效连续介质理论，将裂隙介质等效为多孔介质，参照水文地质手册经验值对模型进行赋值，参数设置见表2。结合模型初始条件和边界条件，确定可能影响含水层孔压扩散的因素，设计不同情景模拟鲁甸地震后含水层孔压扩散的过程，模拟情景设置见表3。采用自由四面体网格剖分计算网格，考虑计算机的算力限制及计算效率，在保证模型计算精度的前提下共剖分5 417 817个网格，模拟时间步长为1 d，模拟时段为研究区0.1 km深度孔压扰动值消散99%以上所需时长。

表2 数值模拟参数

表3 不同模拟情景参数

以鲁甸地震同震静态应变场作为初始条件，对不同模拟情景下研究区含水层孔压扰动及扩散过程进行模拟。初始时刻，研究区孔压分布与同震静态应变场分布一致，但符号相反，最大正、负超孔隙水压变化为分别3.52×10Pa、-3.74×10Pa。研究区内距离断层两端较远的区域产生的同震孔压扰动值在±(10～10)Pa，相较断层两端附近的孔压扰动值小2～3个数量级。

情景1、2模拟不同渗透系数条件下含水层孔压演化规律，如图7所示。模拟结果表明，断层两端的孔压梯度决定了孔压的扩散模式。地下水沿着断层东西两侧的压力最大梯度流动。情景1中含水层孔压经过50 d的演化，孔压变化的最大值已降低了99%以上，孔压基本恢复至震前水平。情景2中鲁甸地震造成的孔压扰动值在低渗透系数模型中经过500 d消散99%以上，基本恢复至震前水平。

图7 在情景1(a)和情景2(b)下模拟不同时间研究区0.1 km深度孔压分布

通过比较情景1、2模拟结果可知，两个模型的孔压消散模式类似，但当渗透系数降低一个量级时，较低的渗透系数使孔压消散的时间增加了约10倍。因此，渗透系数是地震后孔压扩散时长的主控因素，研究区地质介质类型是决定地震后孔压扩散速率的主要变量。

情景3、4分别将孔隙度设置为0.2、0.6，其它条件与情景1保持一致，模拟不同孔隙度对研究区孔压扩散规律的影响。模拟结果显示(图8)，不同孔隙度并不会影响孔压消散模式，在相同时间内不同的孔隙度只会对孔压的消散速率有所影响但影响有限，孔隙度越大孔压消散越慢，不同孔隙度下含水层孔压基本都在50 d内恢复至震前水平。

情景5、6分别将杨氏模量设置为8×10和8×10，其它条件与情景1保持一致，模拟不同风化程度的玄武岩含水层对研究区孔压扩散规律的影响。模拟结果显示(图9)，杨氏模量会显著改变研究区孔压扩散的时间，在其余相同的条件下，杨氏模量越大，孔压扩散时间越短，风化严重的玄武岩孔压会在350 d内恢复至震前水平，而未风化的玄武岩孔压会在20 d内恢复至震前水平。

实际统计结果显示，研究区内多口监测井水位基本均在50 d内恢复至震前稳定值，因此，情景1、3、4模拟得到的孔压恢复时间较为吻合。由模拟结果可知，含水层渗透系数与杨氏模量会显著改变孔压扩散时长，而孔隙度对含水层孔压扩散时长影响较小。

图8 在情景3(a)和情景4(b)下模拟不同时间研究区0.1 km深度孔压分布

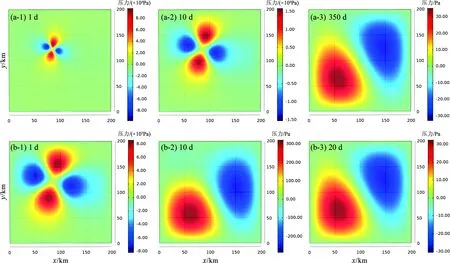
图9 在情景5(a)和情景6(b)下模拟不同时间研究区0.1 km深度孔压分布

3.3.2 压力扰动下含水层-井系统水位响应数值模拟

获得研究区含水层内孔压演化过程后，利用COMSOL Multiphysics中内置的达西定律及层流模块，以静水压强为初始条件，选择情景1中会泽井孔处网格单元含水层平均孔压演化曲线，作为压力扰动下含水层-井系统水位响应模型的边界条件，模拟会泽井水位对鲁甸地震同震响应过程及震后恢复过程，结果如图10所示。

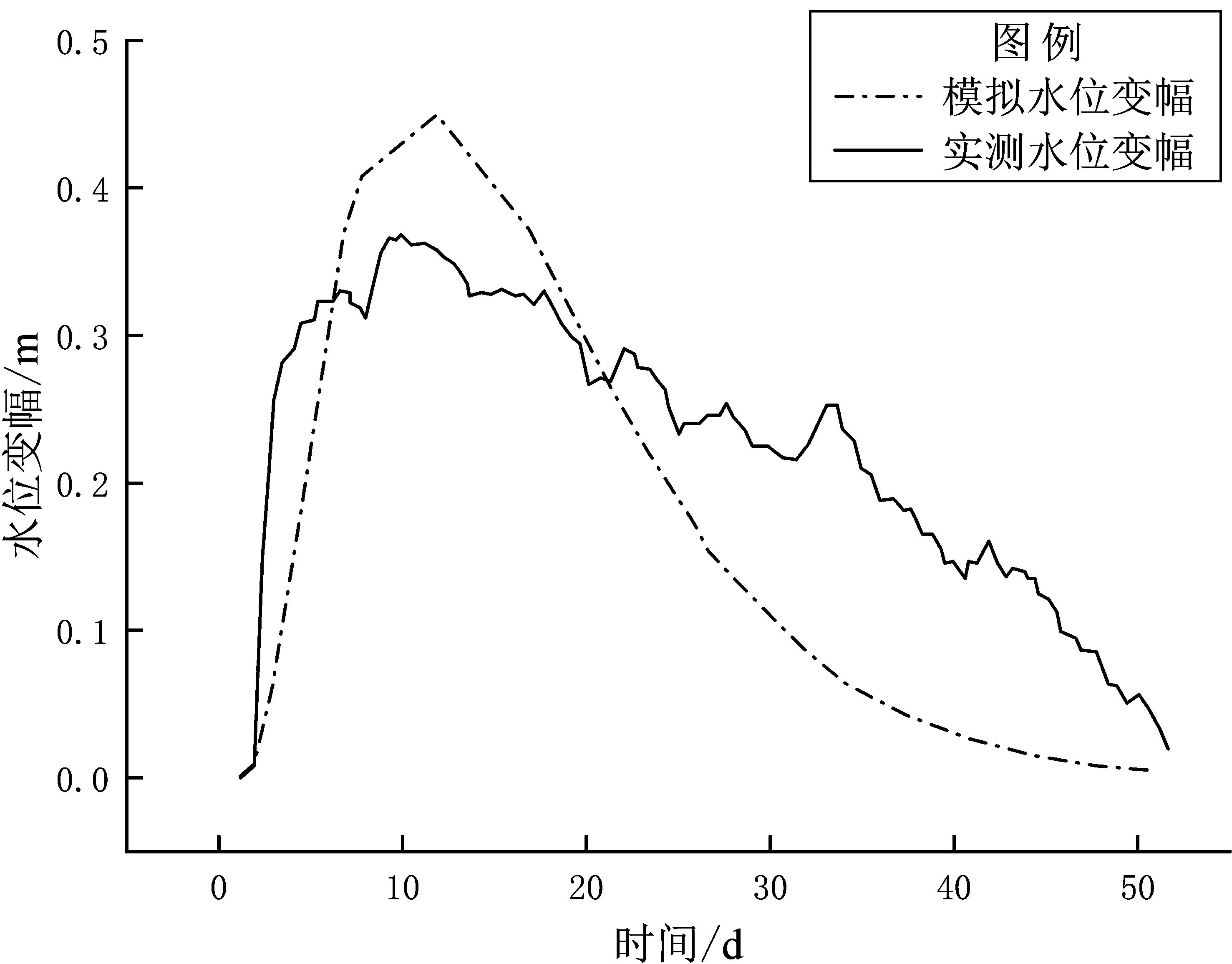
图10 会泽井同震水位变化模拟及实测对比图

模拟结果显示，会泽井水位先呈阶跃上升形式，之后在50 d内恢复至震前水平，井水位最大振幅为0.45 m。模拟与实测水位变化趋势一致，但在水位最大振幅的幅值上有所差异，实测水位最大振幅为0.33 m，较模拟值偏小，可能由于水位同震响应实际上升过程中有井损的产生所导致。震后井水位实测值下降速率较缓，并且在下降期间还存在几次小幅度的上升，查询当地气象资料，发现研究区在8月和9月降雨较多，均匀的降水使井水位恢复曲线较为平缓，但几次暴雨可能使实测水位小幅上升，但也不排除地震或其它构造应力的影响。本文对井水位恢复过程的模拟，未考虑降雨及其他构造应力的影响，因此，模拟与实测水位恢复曲线有所偏差。

3.3.3 模拟计算中存在的不足

首先，本文虽计算出地震造成的同震静态应变场，建立含水层孔压扰动及扩散、压力扰动下含水层-井系统水位响应2个耦合的数值模型，模拟了含水层孔压扰动、井水位响应整个过程，但并未建立表示这一过程的全耦合模型，因此，2个模型耦合项的模拟结果即含水层内孔压的模拟结果会对最终结果产生影响。其次，在含水层孔压扰动及扩散的模拟过程中，未考虑随深度增加温度变化对模拟结果的影响，且未考虑地质体的非均质性对于孔压扩散的影响，这两个因素可能会使最终结果产生误差。同时，本文未考虑降雨、井孔泄压、井损以及其它构造应力对于水位变化的影响，从而导致井水位恢复过程的模拟与实测结果有一定偏差。最后，本文未考虑动态应力造成的渗透性变化导致的水位变化，在今后研究中应考虑该影响。

4 结论

本文以会泽井水位对2014年鲁甸6.5地震同震响应为例，利用数值模拟方法对近场地震水位同震阶变的过程及影响因素进行分析。建立2个耦合模型模拟计算会泽井水位对鲁甸地震的同震响应过程，结论如下：

(1)鲁甸地震造成研究区内地壳压缩区与膨胀区呈四象限分布，压缩区与膨胀区的分界沿断层走向延伸，极值点分布在断层北段两侧，最大压缩应变值为6.56×10、最大膨胀应变值为6.99×10。

(2)同震静态应变场的产生导致研究区内含水层孔压扰动。本文设计6种模拟情景对研究区内孔压的响应与扩散进行模拟，结果表明，影响含水层孔压扰动与扩散的参数为渗透系数与杨氏模量，渗透系数越大，含水层孔压扩散越快，杨氏模量越小，含水层孔压扩散越慢，同时，研究区内多口井水位的实际恢复时间，与各情景模拟孔压恢复时间进行对比，可知研究区实际水文地质参数与情景1、3、4所设置参数相近。

(3)利用压力扰动下含水层-井系统水位响应模型，选取情景1设置模型参数，模拟会泽井孔水位同震响应及恢复过程，得出会泽井水位在同震阶段阶升0.45 m，之后在50 d内恢复至震前水位，模拟结果与实测值在趋势上相符，但由于本模型在研究区内只有一口井，未考虑存在多口井泄压、井损效应及降雨对地下水的补给，因此，对水位的变化细节的刻画还不够精确。