注浆水平纠偏的作用规律与影响因素

程雪松 高洁 潘军 白如冰 郑刚

摘 要：注漿法作为补偿地层沉降的手段已得到广泛应用，目前的研究主要集中于注浆原理及工程沉降纠偏等方面，对于土体参数、注浆参数对隧道水平位移控制效果的影响缺少系统研究。基于天津某工程现场注浆试验，采用应变法模拟注浆过程，研究土质条件、注浆量、注浆距离、注浆长度及注浆深度对注浆水平纠偏效果的影响。结果表明：注浆引起的土体最大水平位移位于注浆体顶部附近;土体强度、刚度参数对注浆效果影响不大，说明注浆控制水平位移的适用性较广泛;距离注浆点较近的土体水平位移随注浆量的增加增长较快，较远时增长较慢，且土体水平位移随注浆距离的增加衰减迅速，应尽量缩短注浆点与纠偏对象的距离;注浆长度较小时，注浆作用范围集中且土体最大位移值较大，反之，注浆作用分散较且均匀，应根据注浆距离和纠偏对象在深度上的范围选择注浆长度，最大化发挥注浆纠偏效果。

关键词：注浆法;土体参数;注浆参数;水平位移

中图分类号：TU433 文献标志码：A 文章编号：2096-6717（2022）05-0136-12

收稿日期：2020-09-27

基金项目：天津市自然科学基金（18JCQNJC07900）;国家自然科学基金（41630641）

作者简介：程雪松（1985- ），男，博士，副教授，主要从事土力学及岩土工程研究，E-mail：cheng_xuesong@163.com。

Received：2020-09-27

Foundation items：Natural Science Foundation of Tianjin （No. 18JCQNJC07900）; National Natural Science Foundation of China （No. 41630641）

Author brief：CHENG Xuesong （1985- ）， PhD， associate professor， main research interests： soil mechanics and geotechnical engineering， E-mail： cheng_xuesong@163.com.

Effect and influencing factors of the grouting on the horizontal deformation control

CHENG Xuesong， GAO Jie， PAN Jun， BAI Rubing， ZHENG Gang

（a. Ministry of Education Key Laboratory of Coast Civil Structures and Safety; b. College of Civil Engineering， Tianjin University， Tianjin 300072， P. R. China）

Abstract：Grouting method has been widely used as a measure to compensate the ground settlement. Current research mainly focuses on the principle of grouting and the recovery of the settlement. However， the influence of soil parameters and injection parameters on the horizontal displacement of tunnel has not been systematically studied. Therefore， based on a field grouting test of a project in Tianjin， this paper used strain method to simulate the grouting process， and studied the influence of soil conditions， grouting amount， grouting distance， grouting length and grouting depth range on the horizontal deformation of soil. The results show that the maximum horizontal displacement of soil caused by grouting is located near the top of the grouted zone. Soil strength and stiffness have little influence on grouting effect， which indicates that the applicability of grouting to control horizontal displacement is wide. The horizontal displacement of soil near the grouting point increases rapidly with the increase of grouting amount and slowly when it is far from the grouting point， and the horizontal displacement of soil decreases rapidly with the increase of grouting distance. Therefore， the distance between the grouting point and the correcting object should be shortened. When the grouting length is small， the influence range of grouting is concentrated and the maximum displacement of soil is large. On the contrary， the influence of grouting is relatively dispersed and uniform. The grouting length should be selected according to the distance of grouting and the range of depth of correcting object to maximize the effect of grouting correction.

Keywords：grouting method; soil parameters; injection parameters; horizontal displacement

注浆法利用浆液体积的膨胀引起周围土体位移场的变化，从而对工程施工引起的土体及结构物的变形进行补偿。目前，关于注浆法的原理及其工程应用的研究已经取得了一定进展。

对注浆抬升地层的研究往往通过数值模拟的方法进行，不同学者对地层抬升的模拟方法不同。唐智伟等采用镜像原理计算注浆引起地层抬升的解析解，并运用FLAC 3D软件，通过在单元上施加膨胀压力模拟注浆抬升过程。侯艳娟等在研究中采用ABAQUS软件，通过施加各向同性面力的方法模拟抬升力。Zhang等采用FLAC 3D程序将灌浆区简化为一系列球形灌浆球筒模拟注浆体的非均匀膨胀过程。Zhang等通过对盾构开挖引起的隧道周围扰动区施加规定的体积应变，模拟注浆对长期地表沉降演化以及地表损失的影响。

关于注浆过程的理论研究也在不断发展。Li根据松散地基的不均匀分布模式，推导了地表沉降与理论注浆量的关系，结果表明，地表沉降最大值与注浆量呈线性关系。Guo等采用随机介质理论计算注浆引起的地表位移，分析了不同注浆条件下各参数对隆起位移的影响，地表隆起位移随注浆深度的增大而减小，随浆液扩散半径、注浆压力的增大而增大。周茗如等基于结构性黄土剑桥模型的圆孔扩张理论，考虑排水条件建立了基于扩孔理论的劈裂注浆起裂压力分析模型，推导了塑性区、破坏区半径及竖向、水平劈裂注浆压力的理论解。魏久传等运用步进式算法进行了动参量裂隙注浆扩散机制的研究，阶段式递降速率裂隙注浆可有效降低注浆终压，阶段式梯级增压裂隙注浆可有效增加浆液的最大扩散距离。

注浆法的应用研究往往出于工程需要。张晨介绍了微扰动注浆技术在控制隧道变形中的应用，微扰动注浆可有效加固土体、减小隧道收敛变形。高永将微扰动双液注浆技术适当调整后应用于南京地铁隧道，该方法适用性良好。Zhu等对深圳地铁隧道的监测数据进行了分析，结果表明，注浆后隧道的水平收敛、椭圆度均减小。郭健对隧道注浆抬升的地层情况进行了研究，结果表明“上软下硬”地层中隧道抬升效果最好。朱瑶宏等通过注浆法对软土地层的隧道沉降进行补偿发现，隧道抬升稳定后，将双液浆替换成单液浆效果更明显。

除了工程实践、理论分析及数值模拟研究，很多学者也采用注浆试验的方法开展研究。Shimada等通过注浆试验，揭示了注浆材料的性状与土体变形的关系，利用两阶段灌浆可将透水性土改良为不透水性土。Zheng等进行了室内注浆试验，结果表明，在低固结度的欠固结土中进行注浆，可以获得较短的初固结时间和较高的初固结末注浆效率。郭佳奇等进行了粉细砂地层注浆模型试验，结果表明，超细水泥比水玻璃更适合加固粉细砂地层。Wang等通过室内注浆试验，研究了压力注浆的主要特点以及随着灌浆压力的增大不同灌浆的扩散模式。

近些年，由于城市的发展，在盾构隧道附近进行基坑工程施工的案例屡见不鲜。由于基坑开挖引发的基坑外土体变形常常会引发临近隧道產生朝向基坑的水平位移及变形，若隧道变形过大，则极易导致隧道管片开裂、错台，甚至渗漏，对隧道的结构安全及地铁列车运营造成重大影响。由此，目前注浆技术也已成功应用于基坑引发的隧道水平位移的控制与恢复。郑刚等通过现场注浆试验，研究了袖阀管注浆过程中相关参数对周围土体水平位移的影响，并为注浆方案选择提供了建议。郑刚等通过实测数据和数值模拟结果，分析了主动注浆控制隧道变形的效果，建议隧道纠偏时采用“近距离、多孔位、小方量”的注浆方案。朱旻等结合模型试验和有限元模型研究了不同注浆压力和注浆位置下隧道变形的发展规律。

高翔等通过有限元软件ABAQUS建立了考虑浆液注入的二维流固耦合模型，对通过打设斜管注浆对隧道进行竖向纠偏的规律进行研究。

然而，虽然目前在注浆理论及注浆抬升工程应用方面已有较多研究，但针对注浆过程中土体参数和注浆参数对注浆控制水平位移效果的影响缺乏系统研究，限制了注浆在控制隧道水平位移及变形方面的应用。笔者基于天津地区的一个注浆控制土体水平位移试验，利用大型有限元计算软件PLAXIS开展了注浆控制土体水平位移的系统模拟，研究土质条件、注浆量、注浆距离、注浆长度及注浆深度对土体水平位移注浆控制效果的影响规律。

1 现场注浆试验及有限元模型

1.1 现场注浆试验

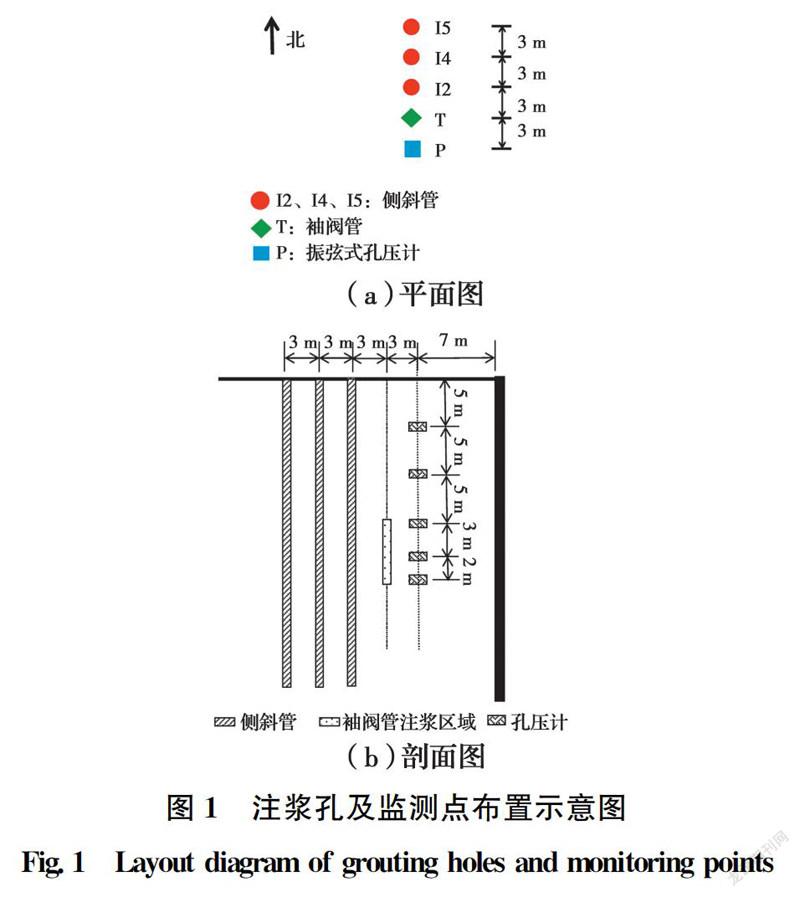
选择天津市某基坑工程与既有地铁隧道结构之间的场地开展注浆原位试验。试验场地与地铁隧道距离超过20 m，距离基坑地连墙10 m，由于试验场地与隧道及基坑的距离均较远，可以认为基坑及隧道对注浆试验无影响。试验采用单根袖阀管注浆，袖阀管T的注浆量为2 m，注浆孔位到基坑地连墙的距离为10 m，试验过程中布置高精度测斜管测量土体的水平位移，注浆孔及监测点布置如图1所示。天津地区的地铁隧道直径通常是6.2 m，隧道顶部

埋深大部分分布在10～20 m，因此，注浆范围取埋深15～20 m。

根据《城市轨道交通結构安全保护技术规范》，盾构隧道周边3 m范围内不得进行任何施工，因此，3个测斜孔I2、I4、I5到注浆孔的距离分别取3、6、9 m。采用振弦式高精度孔压计测量注浆孔附近孔压的变化，在袖阀管另一侧距离3 m的位置沿土深方向布置孔压计，孔压计P1～P5的埋置深度分别为5、10、15、18、20 m。

试验采用水泥水玻璃化学双液浆，配比为水泥∶水玻璃∶水=1∶2.5∶3.43，浆液速凝时间为20 s。根据工程经验，注浆速率为15～20 L/min，注浆压力值为0.3～1.0 MPa。

1.2 有限元模型

采用PLAXIS 3D有限元软件模拟注浆过程，土体本构模型采用小应变硬化模型，即HSS模型。采用应变法对注浆过程进行模拟，参数设置主要包括膨胀范围及膨胀量，膨胀范围指发生压密注浆和劈裂注浆的区域。通过对选定的膨胀范围施加膨胀量来模拟压密和劈裂过程，模拟计算注浆过程中周围土体的位移情况。膨胀量通过对膨胀范围施加体积应变ε来实现，计算如式（1）所示。

ε=VV×100%（1）

式中：V为注浆量;V为模拟中选定的膨胀范围的体积。

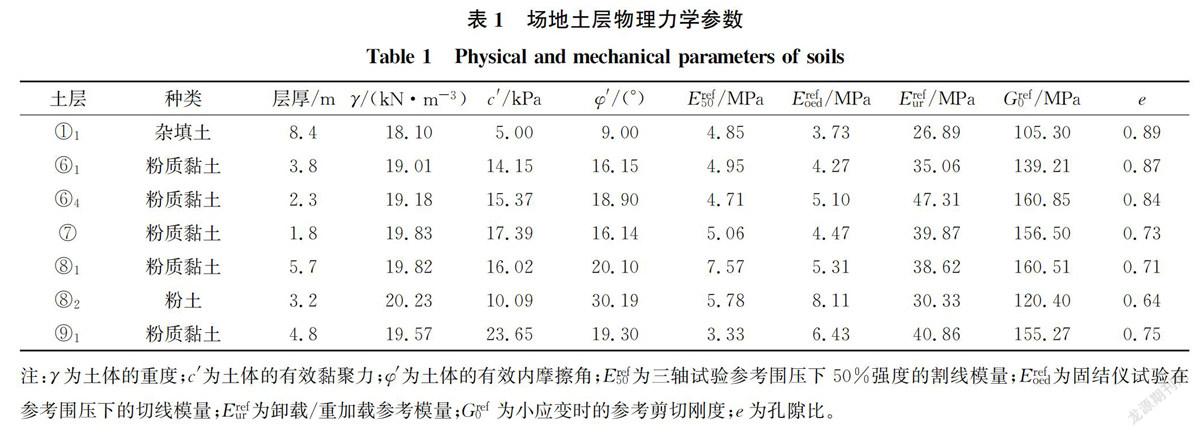
土体物理力学参数及开展有限元分析所需的HSS模型参数均为采用薄壁取土器取样后进行室内试验所得。通过慢剪试验得到土体的有效黏聚力c′和有效内摩擦角φ′。土样刚度通过三轴固结排水试验测定，围压取100 kPa，割线模量E为应力应变曲线中破坏应力一半值所对应点与原点连线的斜率，主固结仪加载中的割线刚度E等于侧限压缩模量，卸载/重新加载刚度E可通过三轴加卸载排水试验得到。初始剪切模量G按照工程经验取G=2.7E。土体物理力学参数见表1。

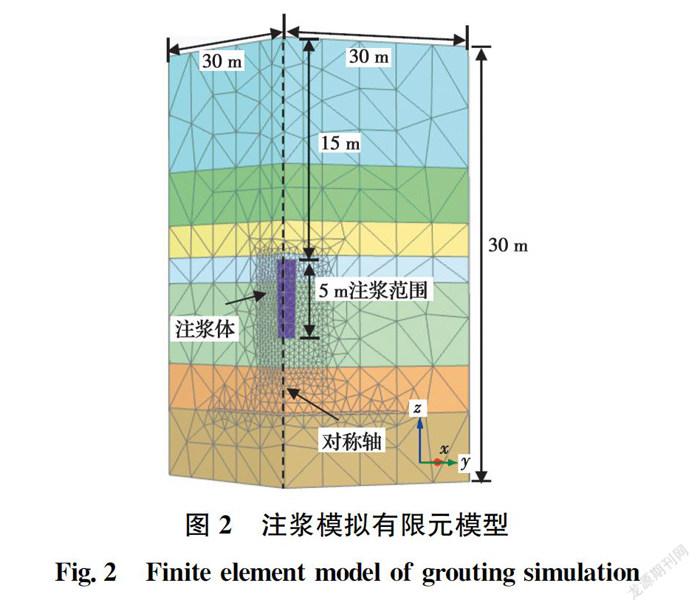
单孔注浆为轴对称问题，建立几何模型时只需按照对称性原则建立1/4模型。规定坐标系统时，选择与注浆中心线重合的方向为z轴，在与之垂直的平面上正交的两个方向分别为x轴、y轴。假定注浆膨胀范围为半径0.8 m的圆柱体。按照试验设计，注浆埋深为15～20 m，注浆长度为5 m。为消除边界效应的影响，模型在x轴、y轴、z轴方向上的长度均取30 m。模型的边界条件采取上边界为自由边界，下边界为固定边界，水平方向采用水平约束。

为了考虑注浆体非均匀膨胀、土体超固结比及超孔压消散裂隙的影响，在距离注浆孔1.5 m的位置设置孔压消散面单元。采用固结算法考虑注浆结束后超孔压消散效应。注浆模拟的有限元模型如图2所示。

1.3 现场试验结果与有限元计算结果的对比

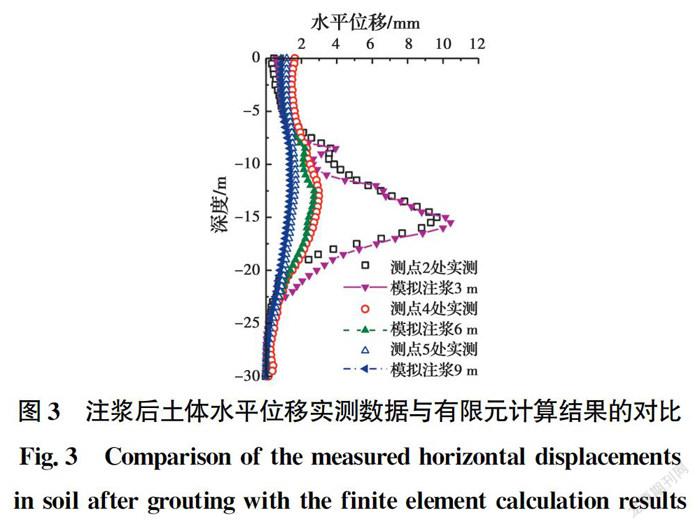
将注浆后土体水平位移的有限元计算结果与实测数据进行比较，如图3所示。注浆距离取3 m时，土体水平位移沿深度方向先增加后减小，并且在埋深15 m附近取得位移最大值。随着注浆距离的增大，土体位移减小，同时，注浆体附近的土体产生的水平位移与地表处及土体深层的水平位移值差异减小，土体变形最值点的埋深逐渐上移。该结论与郑刚等的实测数据的规律一致。分析其原因，注浆距离较小时，注浆效果主要集中于注浆体周围，当注浆距离增大，注浆体膨胀推动土体变形的作用随着向远处传播逐渐减小，并且注浆体以上范围的区域内土压较小，导致该部分土体更容易发生变形。

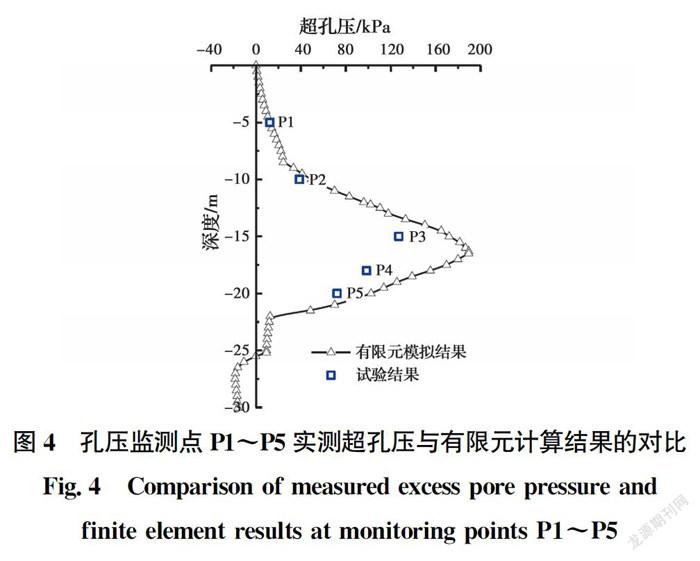
由图3可以看出，测斜孔I2、I4、I5的土体水平位移实测数据与有限元模拟中距离注浆孔3、6、9 m位置处土体水平位移的计算结果吻合较好，土体水平位移沿深度方向近似于15 m埋深的对称分布。将孔压监测点P1～P5监测的注浆体周围土体的超孔压实测值与有限元计算结果比较，如图4所示，两条曲线规律一致，同时，孔压沿深度方向的变化规律也与土体水平位移的规律一致。总体来讲，可认为采用该数值模型得到的结果可靠。

2 数值模拟研究工况

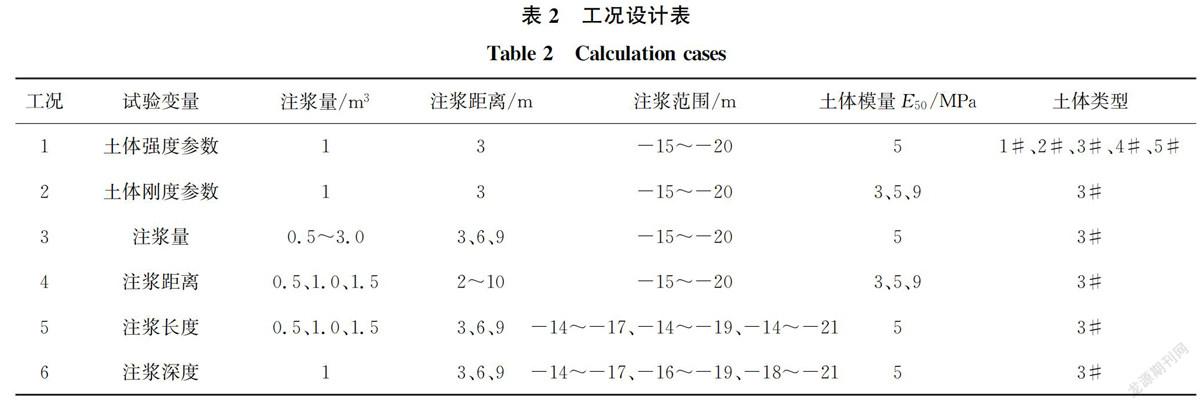
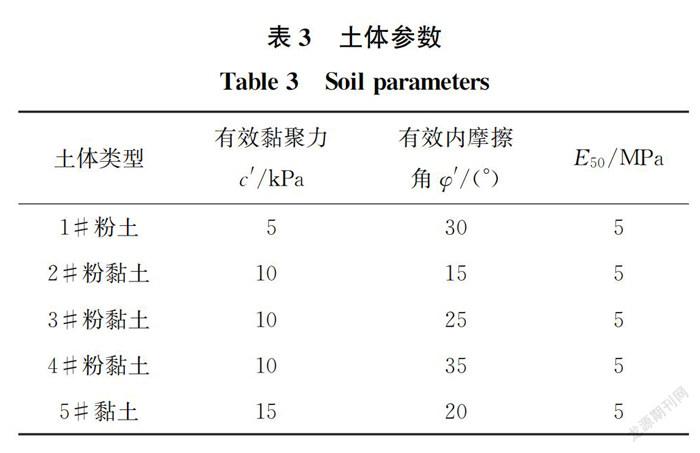
利用上述有限元模型，进一步研究土体参数变化和注浆参数变化对注浆效果的影响，工况设计见表2。数值模拟时为简化计算过程，采用单一土层建立有限元模型，不同参数如表3所示。由于研究对象多样，为分析尽量多的变量影响，在确定唯一主要变量的条件下，也可变化其他参数来研究土体变形规律。划分工况类别时以主要变量为依据，研究工况包括6种，分别是土体强度参数、土体刚度参数、注浆量、注浆距离、注浆长度以及注浆深度作为主要变量的情况。

3 模拟结果

3.1 土质条件对注浆效果的影响

3.1.1 土体强度参数对注浆效果的影响

天津地区的地铁隧道所处地层往往也是注浆所处地层，土体类型主要是黏土、粉土和粉质黏土。通过统计天津地区不同隧道的土层条件，得到土体参数的变化范围，其中，粉土的黏聚力为5～20 kPa，摩擦角为30°～40°;粉质黏土的黏聚力为10～25 kPa，摩擦角为15°～35°;黏土的黏聚力为15～30 kPa，摩擦角为10°～25°。为讨论不同土体强度参数对注浆效果的影响，假定其他参数相同，仅改变5种土体参数，其中1#是粉土、2#是粉黏土、3#是粉黏土、4#是粉黏土、5#是黏土，以上土体参数取值情况见表3。

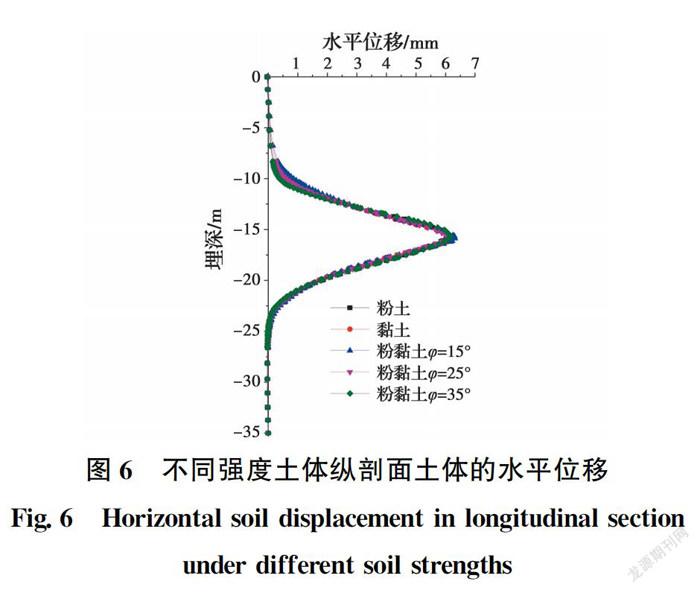
选取埋深为15 m处（注浆范围顶部）的土体为研究对象，注浆量取1 m，将注浆后土体水平位移与土体到注浆中心点距离的关系绘制成曲线，如图5所示。从图5可以看出：当注浆量一定时，5种土体强度参数的曲线变化规律相同，土体水平位移与距离注浆点的远近呈负相关关系，并且衰减速率随着土体与注浆点距离的增加而逐渐减小。注浆后土体水平位移随深度变化的关系如图6所示，可以看出，土体水平位移随埋深的增加先增大后减小，注浆后产生的土体水平位移最大值接近。总体上看，取不同的土体强度参数时，土体水平位移沿水平方向以及沿深度方向的变化规律一致且数值差别不大，因此，可认为土体强度参数对土体水平位移影响较小。

3.1.2 土体刚度参数对注浆效果的影响

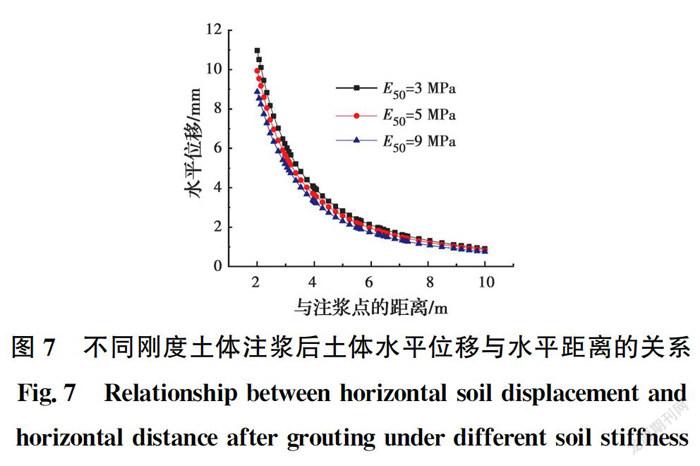
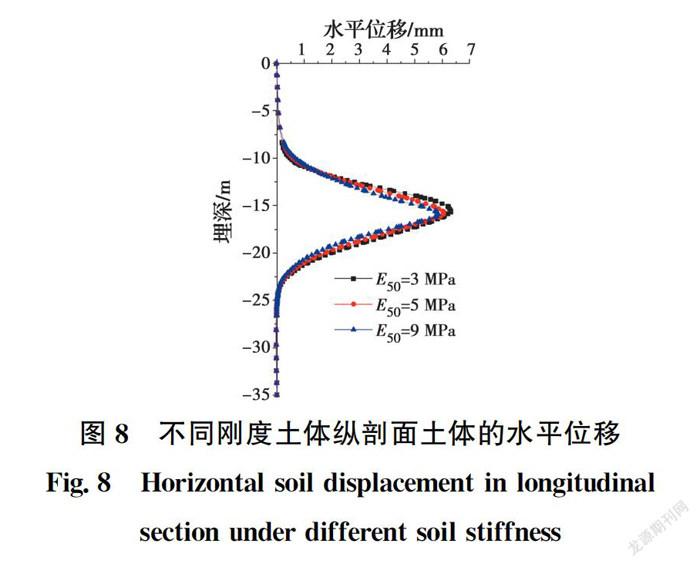
统计天津地区地铁隧道所处土层的刚度范圍，粉质黏土的再压缩模量为15～35 MPa，HSS本构模型中E与该值接近，且E=5E，因此，分别取E=3 MPa、E=5 MPa、E=9 MPa。土体强度参数与3#粉黏土一致，黏聚力为10 kPa，摩擦角为25°。采用小应变土体硬化模型，按照工程经验取E=E、E=5E、G=2.7E。注浆量取1 m，注浆范围取15～20 m。注浆范围顶部的土体位移随水平距离的变化情况如图7所示。距离注浆孔3 m的土体水平位移随深度的变化情况如图8所示。

由图7可知，土体刚度越小，注浆引起的土体水平位移越大，这是由于土体刚度较大时，注浆体膨胀受到周围土体的约束较大，因而对土体产生的推动作用较小。

从数值上看，刚度变化2 MPa时，土体位移的差值最大是1 mm左右，位移变化不大。由图8可知，土体刚度变化时，注浆后土体水平位移随深度变化的规律与前述相同，近似于15 m埋深位置的对称分布。在注浆量一定时，E数值逐渐增大，导致水平位移曲线向纵坐标轴靠近，包络范围随之逐渐减小，即注浆补偿效果减弱。

总体上看，对于软土地层，土体强度与刚度参数对注浆效果的影响不大，注浆法可广泛采用。

3.2 注浆量对土体水平位移的影响

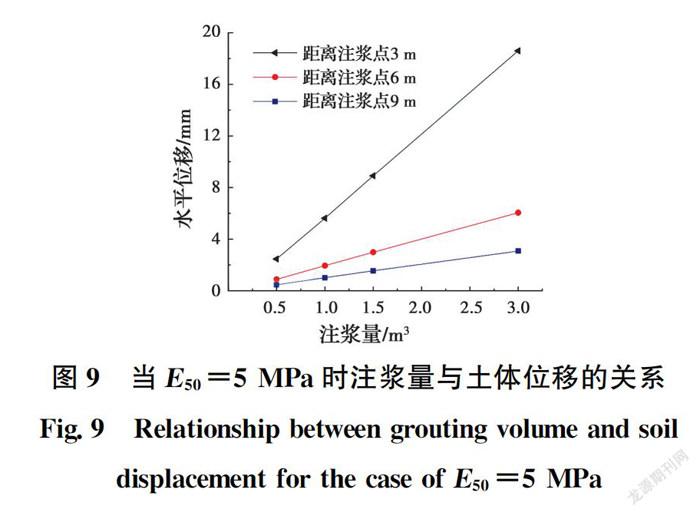
结合工程实际，注浆量在0.5～3 m范围内变化取值，比较不同注浆量下的土体水平位移。当注浆量处于0.5～1 m范围时，间隔0.1 m进行取值。当注浆量处于1～3 m范围时，间隔0.5 m进行取值。土体类型为黏聚力10 kPa、摩擦角35°的粉黏土，刚度参数为E=5 MPa，注浆深度为埋深15～20 m。以距离注浆孔3、6、9 m处的土体为研究对象，将埋深为15 m处的土体水平位移与注浆量之间的关系做成曲线图，结果如图9所示。

由图9可见：1）土体水平位移与注浆量呈正相关线性关系，并且该关系形式与土体到注浆点的距离无关;2）土体距离注浆点较近时，土体水平位移随注浆量的增加而快速增加，注浆效果显著;3）距离注浆点越远的土体，其水平位移随注浆量变化的速率越小。若使土体发生4 mm的水平位移，当注浆点距离纠偏对象3 m时，注浆量需要0.7 m左右，而当注浆点距离纠偏对象9 m时，则需要的注浆量大于3 m。因此，在利用注浆纠偏隧道的工程实践中，为保证同等注浆量下获得的注浆效果最优，注浆位置应尽量选择在靠近隧道的区域。

3.3 注浆距离对土体水平位移的影响

选取3种注浆量分别为0.5、1.0、1.5 m，3种土体刚度参数E分别为3、5、9 MPa，土体类型为黏聚力10 kPa、摩擦角35°的粉黏土，注浆深度为埋深15～20 m，对埋深为15 m位置的土体进行分析。

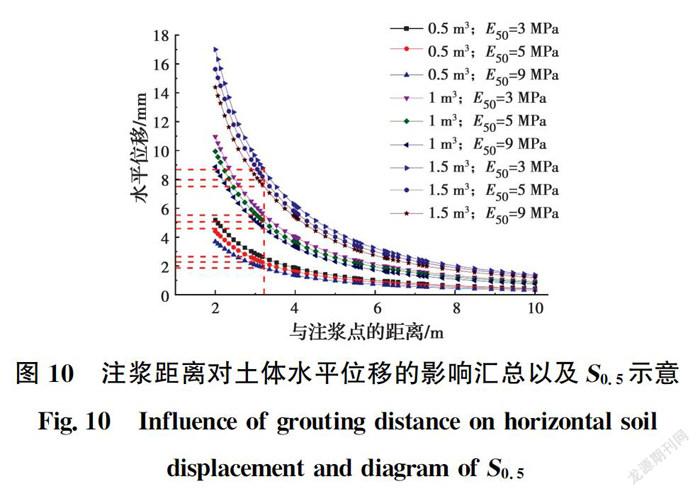
将以上几种注浆条件下注浆距离与土体水平位移的关系归纳在一张图上，结果如图10所示。由图10可见：1）在注浆量一定时，土体水平位移随着与注浆点距离的增加而减小，并且减小速率逐渐变缓，土体水平位移逐渐趋向某一稳定值;2）在相同的土体模量条件下，注浆量增加使注浆点附近土体的水平位移明显增加，而远处土体的位移变化较小;3）土体刚度的提高会使土体水平位移稍微减小，而随着与注浆点距离的增加，这种变化趋于不明显。注浆距离的改变对注浆效果的影响更加直观，在注浆纠偏隧道的过程中，要重点考量注浆点的位置，如果注浆距离过大，将不能充分利用注浆体的变形控制优势，达不到预计的注浆效果。

在横坐标上距离注浆点2 m的位置作出一条竖直线，该直线与图中的若干曲线相交可得一系列交点，过以上交点作水平直线即可得到对应位置的水平位移值。以这个位移值为基准，乘以系数0.5，将其作为目标水平位移值，即确定纵坐标位置，之后可以得到曲线上该点的横坐标，即该位置与注浆点的距离。经过以上操作，发现50%位移值对应的横坐标集中在同一位置，与注浆点的距离为3.17 m，与注浆量和土体参数均无关。

如果定义位移基准值的效率为100%，对应的横坐标距离记作S，那么容易得到50%位移值的效率为50%，相应的距离表示为S。从图中可以得到S=2 m，近似地，S=3 m。

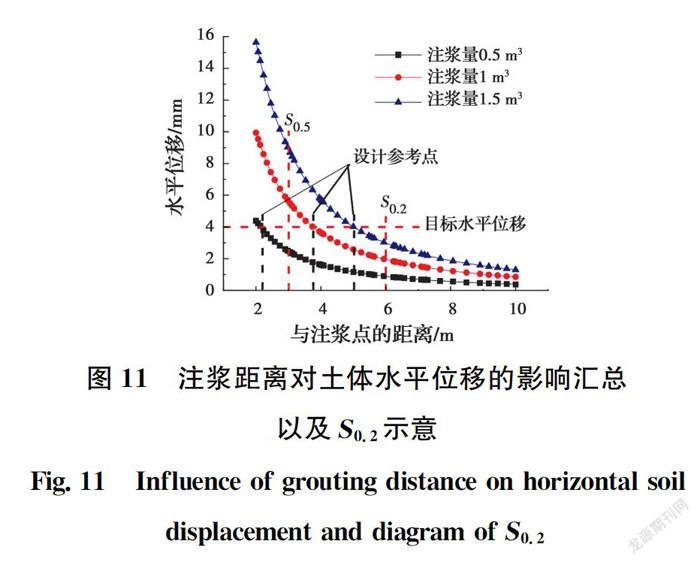
按照相同的方式，可以确定出效率为20%的注浆距离S，如图11所示。同样地，可以发现20%注浆效率的注浆距离与注浆量无关，与土体刚度参数也无关。从图中可以得到S= 5.95 m，近似记作S=6 m。

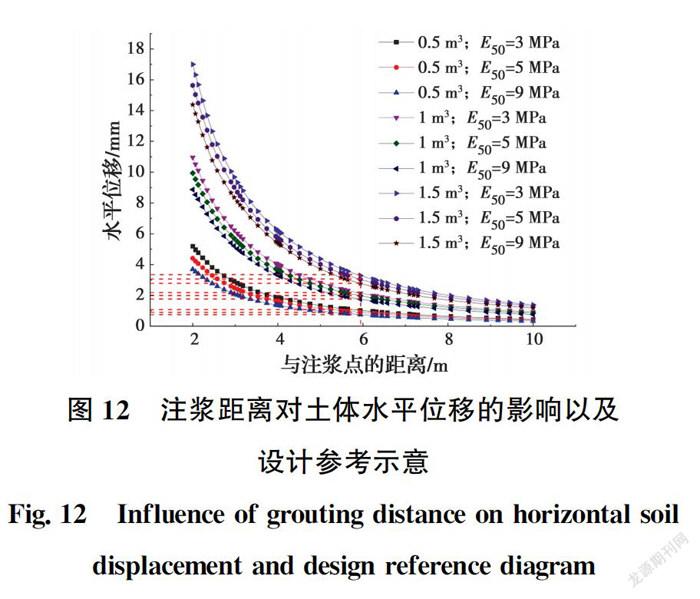
上述结果可以作为注浆距离、注浆量选择的参考依据。具体方法与前述一致，通过在图中作水平、竖向直线的方式，可以确定给定效率值下的水平位移与到注浆点的距离，如图12所示。在实际工程中，除了目标水平位移对应的注浆距离S，可以将S和S作为注浆参数的参考依据，以满足不同点的经济效益要求。

3.4 注浆长度对土体水平位移的影响

3.4.1 注浆长度对土体水平位移沿深度方向变化的影响

注浆长度分别取3、5、7 m，将注浆范围的顶部埋深固定在14 m，即3种注浆范围分别为埋深14～17 m、14～19 m、14～21 m。选取注浆量为1 m，土体类型为黏聚力10 kPa、摩擦角35°的粉黏土，土体模量为E=5 MPa，对距离注浆点3 m的土体进行分析，并绘制土体水平位移随埋深变化曲线，如图13所示。

从图13可见：1）不同注浆长度条件下，土体水平位移均在埋深15 m附近取得最大值，注浆长度增大时，15 m埋深以下的土体位移增大，而15 m埋深以上的土体位移减小，这是由于注浆范围顶部埋深不变，注浆长度增加以后，整个注浆体的中心下移，注浆效果更多作用于下方区域的土体;2）当注浆长度从3、5 m增加到7 m，对应的水平位移最大值分别为7.7、6.1、4.9 mm，注浆长度7 m时的位移最大值相较于注浆长度3 m时的值减小了36.4%，相较于注浆长度5 m时的值减小了19.7%，可以看出，注浆长度较小时，作用力更为集中，土体水平位移最大值较大;3）在埋深17 m以上，相同埋深位置处，注浆长度较小时，土体水平位移更大，在埋深17 m以下，注浆长度较小时，土体水平位移偏小。

综上可以得到：当其他条件一致时，注浆长度增加会导致土体水平位移的最大值减小，同时位移曲线包络线的范围也从窄尖形变化到宽扁形，即注浆长度较小时注浆影响范围集中，注浆长度较大时影响较为分散。在实际纠偏工程中，适量增大注浆长度有助于扩大注浆影响范围，在影响区内发挥注浆体对土体及结构变形的影响作用，使纠偏对象均匀变形，从而达到注浆纠偏的目的。

3.4.2 注浆长度对土体水平位移沿深度方向最值出现位置的影响

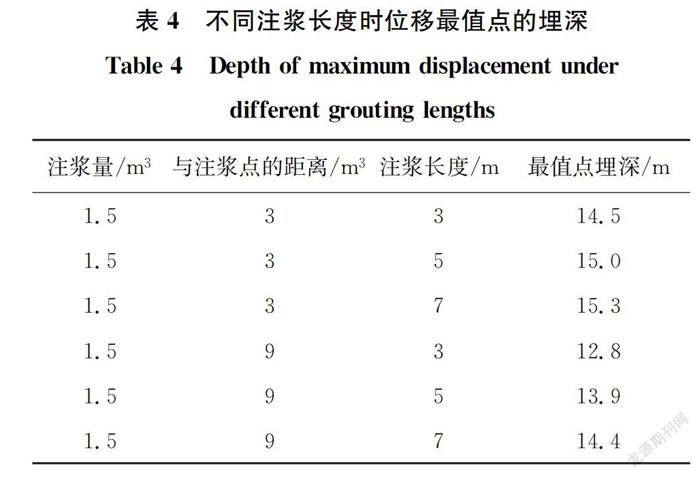
改变注浆长度，对纵深方向上土体水平位移取得最大值的位置进行研究。选取注浆量为0.5、1.0、1.5 m，其他参数均与上文相同，将不同注浆长度下最大水平位移的埋深与土体到注浆点距离的变化关系进行汇总，结果如图14所示。不同注浆长度时，土体水平位移最大值的埋深如表4所示。

由图14可见：1）水平位移最大值集中出现在15 m附近（注浆范围中点的上方），并且土体距离注浆点越远，其水平位移最大值的埋深越小，這是由于距离注浆点较远时，注浆体的膨胀作用沿土体深度方向的影响范围增大，由于上层土体的土压较小，因而注浆体上方土体会产生较大变形;2）由表4可知，在距离注浆点9 m的位置，当注浆量取1.5 m时，注浆长度7 m时最大值的埋深比注浆长度3 m时靠下1.6 m，可以看出，注浆长度增加时，水平位移最大值的埋深随之增加，该结论与郑刚等的研究结论一致，当注浆体底部位置固定时，注浆长度增大，最值点的埋深会上移;3）注浆长度一定时，注浆量增加使位移最大值埋深朝着远离注浆点方向衰减的速率增大，即注浆量越大，远离注浆位置处的土体水平位移最大值埋深越来越浅。

由此可见，在注浆纠偏的实际工程中，需要综合考虑注浆点与纠偏对象的间距、纠偏对象的深度范围等因素，保证注浆影响范围与纠偏对象范围一致，才能达到理想的注浆效果。

3.4.3 注浆长度对土体水平位移沿水平方向分布的影响

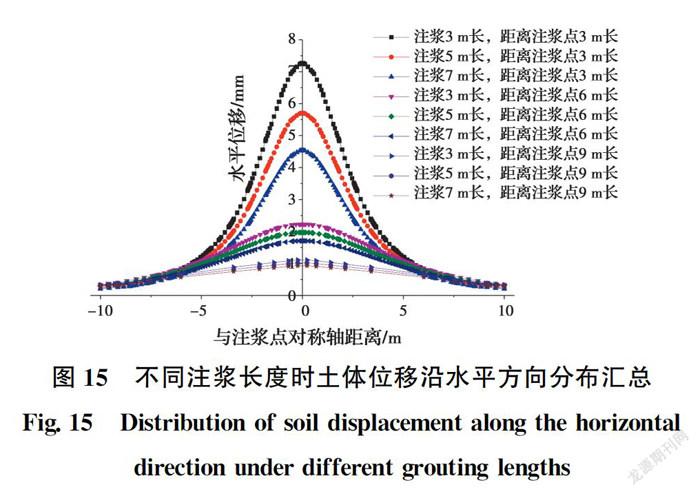
选取注浆量为1.0 m，其他参数均与上文相同，对注浆范围顶部位置（埋深14 m）距离注浆点3、6、9 m的土体进行分析，土体水平位移与土体到注浆点对称轴距离的关系曲线如图15所示。注浆点对称轴处的土体水平位移值见表5。

由图15可见：1）注浆长度较小时，注浆点附近土体产生的水平位移较大，且注浆长度变化对注浆点邻近土体位移变化影响较大，对远处土体位移变化影响较小;2）土体距离注浆点的远近影响土体水平位移的分布形式，距离较小时分布较为集中，距离较远时分布较为分散;3）注浆距离取3 m时，3种注浆长度下的位移曲线相差很大，由表5可知，注浆长度3 m时的最大水平位移值比注浆长度7 m时大1.8 mm，注浆距离取9 m时，3条曲线趋于重合，注浆长度3 m时的最大水平位移值比注浆长度7 m时大0.2 mm。可以看出，注浆距离较远，超出注浆影响范围时，注浆长度对注浆效果的影响可以忽略不计。

3.5 注浆深度对土体水平位移的影响

3.5.1 注浆深度对土体水平位移沿深度方向变化的影响

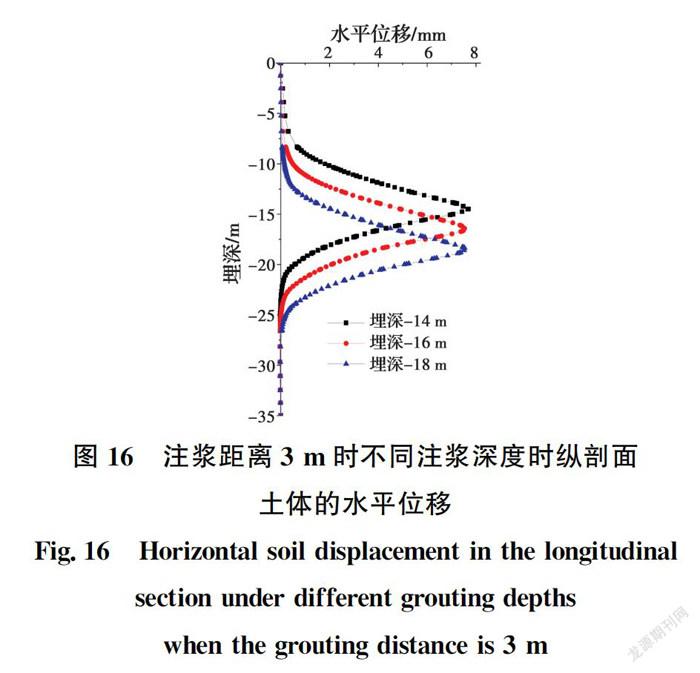
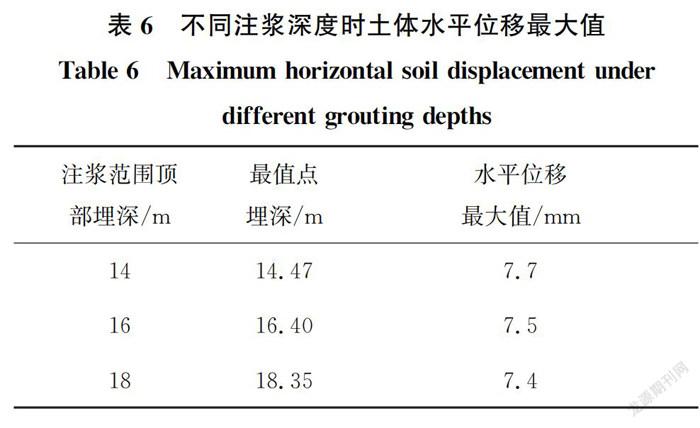
注浆范围顶部埋深分别采用14、16、19 m，注浆长度为3 m，即3种注浆范围分别为14～17 m、16～19 m、18～21 m。取注浆量为1 m，土体类型为黏聚力10 kPa、摩擦角35°的粉黏土，土体模量为E=5 MPa，对距离注浆点3 m的土体进行分析，研究注浆深度变化时土体水平位移随埋深的变化规律，如图16所示。不同注浆深度的土体水平位移最大值见表6。

由图16可见，土体水平位移随埋深变化的曲线均为先增大后减小的右凸曲线，曲线形式发生平移，并不因注浆埋深变化而改变。由表6可知，注浆埋深14、16、18 m的土体水平位移最大值分别是7.7、7.5、7.4 mm，随埋深增加逐渐减小，但总体相差不大。随着注浆范围顶部埋深的下移，曲线发生整体下移。

3.5.2 注浆深度对土体水平位移沿深度方向最大值出现位置的影响

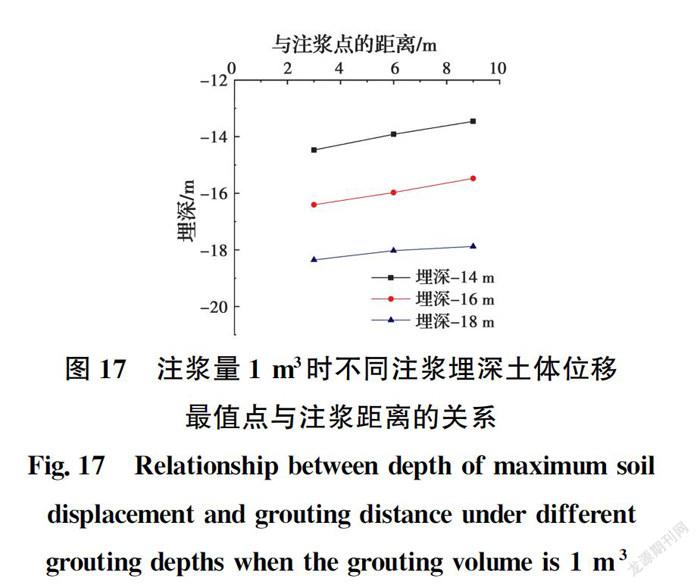
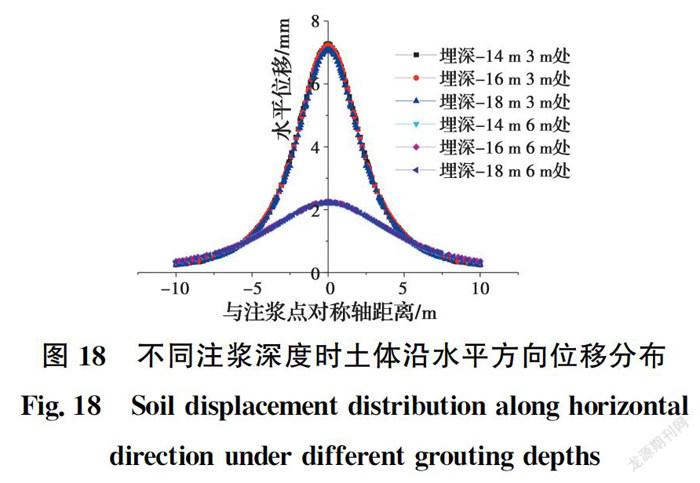
注浆深度及其他参数与上文相同，对比距离注浆点3、6、9 m的土体水平位移取得最大值时的埋深，结果见图17。不同注浆深度时，最值点的埋深见表7。

由图17可见：1）任意埋深情况下，距离注浆点越远的土体，其水平位移取得最大值的位置越靠近地表;2）注浆深度距离地表越远，各点处土体水平位移取得最大值的位置也越深。由表7可知，在注浆距离3、9 m的位置，注浆埋深14、16 m的土体水平位移最大值的埋深差值分别是1.93、2.01 m，注浆埋深16、18 m的最大值的埋深差值分别是1.95、2.4 m，注浆埋深的变化量与最值位置的变化量几乎相同，都在2 m左右。

3.5.3 注浆深度对土体水平位移沿水平方向分布的影响

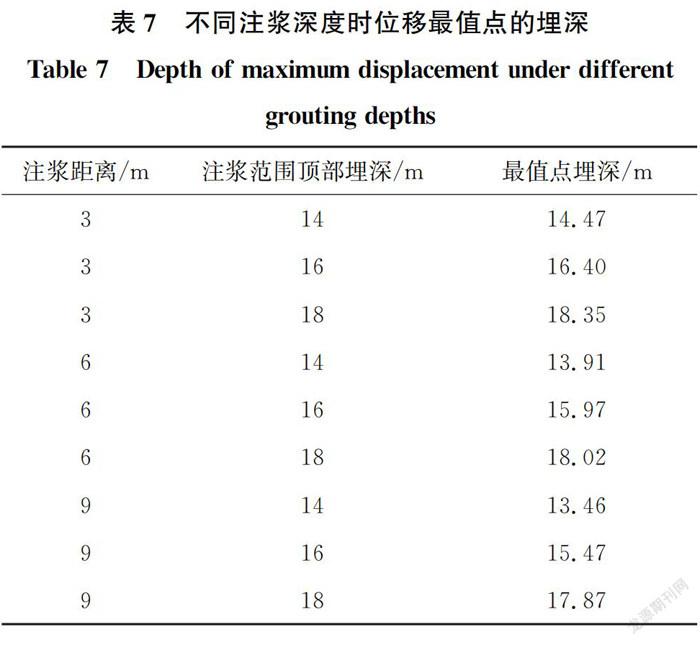
参数选取与上文相同，以距离注浆点3、6 m位置注浆范围顶部的土体为研究对象，分析土体水平位移沿水平方向的分布情况，结果见图18。

由图18可见：1）注浆埋深变化时，土体水平位移在水平方向上的分布规律不变，以注浆点对称轴位置为中心，向两侧同步递减，3条曲线的位移值几乎重合;2）距离注浆点对称轴3 m的土体水平位移值普遍大于距离注浆点对称轴6 m的土体水平位移值，在注浆点邻近区域内，土体的水平位移差较大，而在距离注浆点较远的地方，两种情况的土体位移值接近。

4 结论

在天津市某基坑工程与既有地铁隧道结构之间开展注浆原位试验，建立符合工程实际的有限元模型，并验证其计算结果的可靠性。在此基础上，利用有限元分析注浆引起的土体水平位移沿水平方向和深度方向的分布规律，归纳包括土质条件、注浆量、注浆距离、注浆长度以及注浆深度等参数对注浆后土体水平位移的影响。主要结论如下：

1）注浆引起周边土体产生的水平位移沿深度方向先增大后减小，注浆范围在15～20 m的注浆体引起周边土体在15 m埋深位置取得水平位移最大值。利用注浆法控制纠偏对象水平位移时，注浆范围的顶部應布置在纠偏对象变形最大的位置。

2）土体的强度参数和刚度参数变化仅会小幅影响注浆引起的土体水平位移。对于软土地层，注浆控制隧道水平位移有较好的适用性。

3）距离注浆点较近的土体，其水平位移随注浆量增加而增大的速率较大;距离注浆点较远的土体，其水平位移随注浆量增加而增大的速率相对较小。由此可见，在注浆距离太远时，即使增大注浆量，注浆效果的提升也不显著。

4）当注浆距离增加时，实现相同的注浆效果所需的注浆量会显著增加，例如，产生4 mm的纠偏位移，注浆距离9 m时所需的注浆量比注浆距离3 m时增加3.3倍。因此，选择近距离注浆方案可大幅节省注浆量。

5）注浆距离增加时，土体水平位移逐渐减小，并且衰减速度逐渐放慢，例如，相同埋深位置距注浆点3、6 m处的土体水平位移分别为2 m处的50%与20%。因此，在注浆纠偏隧道时，注浆点应尽可能靠近隧道，否则注浆效果不明显。

6）沿土体深度方向，注浆长度较小时注浆作用范围集中，注浆长度较大时作用范围较为分散;注浆长度增加会导致土体水平位移最大值显著减小及最大值位置略微下移。在制定注浆方案时，应根据纠偏对象的平面位置及深度范围确定注浆深度与注浆长度，将注浆作用最大的深度及范围与纠偏目标对应，最大化地发挥注浆纠偏效果。

参考文献：

[1] 唐智伟， 赵成刚， 张顶立. 地下工程抬升注浆设计方法及其抬升效果预测研究[J]. 土木工程学报， 2007， 40（8）： 79-84.

TANG Z W， ZHAO C G， ZHANG D L. Design of displacement grouting and prediction of the effect for construction of underground structures [J]. China Civil Engineering Journal， 2007， 40（8）： 79-84. （in Chinese）

[2] 侯艳娟， 张顶立， 陈峰宾. 隧道施工下穿建筑物注浆抬升机制及预测研究[J]. 岩石力学与工程学报， 2011， 30（12）： 2407-2415.

HOU Y J， ZHANG D L， CHEN F B. Study of mechanism and prediction of grouting uplift in tunnel construction undercrossing buildings [J]. Chinese Journal of Rock Mechanics and Engineering， 2011， 30（12）： 2407-2415. （in Chinese）

[3] ZHANG M， WANG X H， WANG Y. Numerical evaluation of uplifting effect for upper structure by grouting [J]. Journal of Central South University， 2012， 19（2）： 553-561.

[4] ZHANG D M， HUANG H W， WANG J M. Numerical study on the effect of grouting on long-term settlement of tunnels in clay [J]. Lecture Notes in Computer Science， 2007， 4489： 1114-1121.

[5] LI C L. Simplified algorithm for grouting pressure and grouting quantity in shield construction [J]. International Journal of Civil Engineering， 2020， 18（4）： 419-428.

[6] GUO F Q， LIU X T， TONG W Q， et al. Prediction of ground surface displacement caused by grouting [J]. Journal of Central South University， 2015， 22（9）： 3564-3570.

[7] 周茗如， 卢国文， 王腾， 等. 结构性黄土劈裂注浆力学机理分析[J]. 工程力学， 2019， 36（3）： 169-181.

ZHOU M R， LU G W， WANG T， et al. Mechanism analysis of structured loess fracturing grouting [J]. Engineering Mechanics， 2019， 36（3）： 169-181. （in Chinese）

[8] 魏久传， 韩承豪， 张伟杰， 等. 基于步进式算法的裂隙注浆扩散机制研究[J]. 岩土力学， 2019， 40（3）： 913-925.

WEI J C， HAN C H， ZHANG W J， et al. Mechanism of fissure grouting based on step-wise calculation method [J]. Rock and Soil Mechanics， 2019， 40（3）： 913-925. （in Chinese）

[9] 张晨. 微扰动注浆工艺在地铁保护中的应用[J]. 建筑施工， 2020， 42（7）： 1272-1273，1283.

ZHANG C. Application of micro disturbance grouting technology in subway protection [J]. Building Construction， 2020， 42（7）： 1272-1273，1283. （in Chinese）

[10] 高永. 微擾动双液注浆纠偏技术在南京地铁盾构隧道病害治理中的应用[J]. 城市轨道交通研究， 2015， 18（6）： 109-112，129.

GAO Y. Application of micro disturbance correction technique for double liquid grouting in shield tunnel disease treatment of Nanjing metro [J]. Urban Mass Transit， 2015， 18（6）： 109-112，129. （in Chinese）

[11] ZHU M， GONG X N， GAO X， et al. Remediation of damaged shield tunnel using grouting technique： Serviceability improvements and prevention of potential risks [J]. Journal of Performance of Constructed Facilities， 2019， 33（6）： 04019062.

[12] 郭健. 盾构隧道注浆抬升管片的效率研究[J]. 铁道建筑技术， 2016（9）： 18-20，41.

GUO J. Efficiency of grouting segment uplifting in shield tunnel [J]. Railway Construction Technology， 2016（9）： 18-20，41. （in Chinese）

[13] 朱瑶宏， 夏汉庸， 胡志飞. 软土地层盾构隧道结构整体抬升实践[J]. 岩土力学， 2016， 37（Sup2）： 543-551.

ZHU Y H， XIA H Y， HU Z F. An uplifting practice of shield tunnel in soft ground [J]. Rock and Soil Mechanics， 2016， 37（Sup2）： 543-551. （in Chinese）

[14] SHIMADA H， CHEN Y L， ARAKI K， et al. Experimental and numerical investigations of ground deformation using chemical grouting for pipeline foundation [J]. Geotechnical and Geological Engineering， 2012， 30（2）： 289-297.

[15] ZHENG G， ZHANG X S， DIAO Y， et al. Experimental study on grouting in underconsolidated soil to control excessive settlement [J]. Natural Hazards， 2016， 83（3）： 1683-1701.

[16] 郭佳奇， 王生， 孟长江， 等. 粉细砂地层注浆模型试验研究及工程应用[J]. 科学技术与工程， 2019， 19（24）： 331-337.

GUO J Q， WANG S， MENG C J， et al. Experimental study and engineering application of grouting model in silty sand stratum [J]. Science Technology and Engineering， 2019， 19（24）： 331-337. （in Chinese）

[17] WANG Q， WANG S Y， SLOAN S W， et al. Experimental investigation of pressure grouting in sand [J]. Soils and Foundations， 2016， 56（2）： 161-173.

[18] 郑刚， 王若展， 程雪松， 等. 注浆对邻近土体水平变形影响的原位试验研究[J]. 天津大学学报（自然科学与工程技术版）， 2019， 52（9）： 959-968.

ZHENG G， WANG R Z， CHENG X S， et al. In situ test study of influence of grouting on horizontal deformation of adjacent soil [J]. Journal of Tianjin University （Science and Technology）， 2019， 52（9）： 959-968. （in Chinese）

[19] 郑刚， 潘军， 程雪松， 等. 基坑开挖引起隧道水平变形的被动与注浆主动控制研究[J]. 岩土工程学报， 2019， 41（7）： 1181-1190.

ZHENG G， PAN J， CHENG X S， et al. Passive control and active grouting control of horizontal deformation of tunnels induced neighboring excavation [J]. Chinese Journal of Geotechnical Engineering， 2019， 41（7）： 1181-1190. （in Chinese）

[20] 朱旻， 龚晓南， 高翔， 等. 盾构隧道注浆纠偏模型试验研究[J]. 铁道科學与工程学报， 2020， 17（3）： 660-667.

ZHU M， GONG X N， GAO X， et al. Model tests of correction of displaced shield tunnel using grouting technique [J]. Journal of Railway Science and Engineering， 2020， 17（3）： 660-667. （in Chinese）

[21] 高翔， 龚晓南， 朱旻， 等. 盾构隧道注浆纠偏数值模拟研究[J]. 铁道科学与工程学报， 2020， 17（6）： 1480-1490.

GAO X， GONG X N， ZHU M， et al. Numerical simulation of grouting remediation in shield tunnel [J]. Journal of Railway Science and Engineering， 2020， 17（6）： 1480-1490. （in Chinese）

（编辑 王秀玲）