梁式桥梁应变模态振型识别研究

耿 栋，王 乐，蒋 鹏

（1.安徽省公路工程检测中心，安徽 合肥 230051；2.桥梁与隧道工程检测安徽省重点实验室，安徽 合肥 230051）

在桥梁结构动力特性研究中，模态试验是一项重要内容，反映结构固有自振特性。对于线性结构来说，自由振动是由N个正交的单自由度振动子系统耦合的系统，每一个单自由度振动即对应结构的一个模态，所以结构振动系统包含N个模态。每一个模态包含多个参数，比如模态振型、模态频率及模态阻尼。模态试验就是为获得这些参数的试验分析过程。现如今，在桥梁模态试验中，模态分析基本都是分析结构的位移模态，模态试验基本以采集结构的动态速度、加速度为主。位移模态的分析、处理技术已经较为成熟，取得了许多研究成果[1]。然而，仅仅进行位移模态分析研究并不能完全反映所有桥梁动力特性。比如，当桥梁出现裂缝，也就是出现应力集中现象时，结构位移模态分析则无法反映。当结构局部振动过大，或是受到振动干扰源影响时，位移模态分析也不能够反映出结构的变化情况。相对于位移模态，应变模态是结构另外一种能量平衡状态表现的形式。与位移模态相比较，应变模态分析则能反映结构局部的微小变化，比如结构出现裂缝，结构的局部应变就会发生变化，裂缝处会出现应变集中现象，这些变化都会反映在结构应变模态分析当中[2]。同时在复杂结构研究中，分析环境变化对结构产生内力影响时，仅仅通过位移模态分析并不能获取全部想要的结果，无法反映复杂环境下结构的应力变化情况，这时候应变模态则是必不可少的测试内容。此外，应变模态也可被用于梁结构的动挠度识别研究，且有较好的精度[3]。

模态振型是模态试验中的一个重要参数，通俗地讲是每阶模态振动的形态。从数学上讲，模态振型就是模态空间中的“基”向量。位移模态振型是结构上的节点或测点的位置函数，应变模态振型则是结构上的节点或测点的应变函数。对于如何获取应变模态振型，国内外学者做了大量研究工作，提出较多识别方法。1995年，张开银通过运用结构的应变叠加原理，采用ITD法对悬臂梁结构进行了应变模态振型分析。2002年，LI等人利用瑞利－里兹方法来识别应变模态振型。近年来，基于随机子空间的应变模态参数识别方法也被越来越多人熟知[4]。此外，针对梁式结构利用互相关函数法获取应变模态振型也被证明是一个有效的方法，该方法是通过实测动态应变数据直接计算应变模态振型，方法简单易行[5]。

本文研究基于位移和应变的相互变换关系识别梁式桥梁应变模态振型，本文研究重点为位移和应变的相互变换关系及位移模态和应变模态在模态振型上的转换关系。为验证基于位移和应变的相互变换关系识别梁式桥梁应变模态振型的有效性、准确性，本文利用有限元计算软件分别对简支梁、连续梁进行了数值模拟。

1 方法与理论

桥梁结构在环境激励（比如行车、行人、地脉动、风荷载等）的作用下，会发生随机的振动。假设梁结构沿纵向坐标在x位置处，在t时刻下的位移和应变可分别表示为公式（1）和公式（2）：

公式（1）和公式（2）中，Φi（x）和Ψi（x）分别表示为第i阶次位移模态振型函数和第i阶次应变模态振型函数在梁结构纵向x坐标处的函数值，ηi（x）为第i阶次模态坐标函数在t时刻的函数值。

按照梁结构的相关原理，梁结构的位移和应变之间的转换的关系可表达为下式：

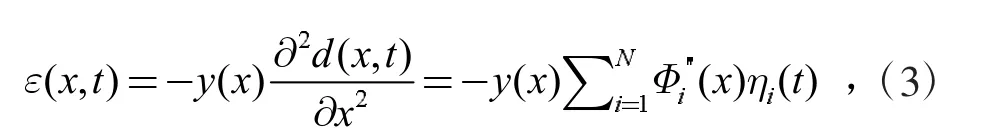
公式（3）中，y（x）为梁结构在纵向x坐标处，梁截面的中性轴在梁高方向上距梁底的距离，关于中性轴在梁横截面上的位置，可根据截面尺寸计算获得，或通过平行的应变测试识别[3]。

根据公式（3）和公式（2），可获得第i阶次应变模态振型函数与第i阶次位移模态振型函数相互之间的转化关系：

通过对公式（4）进行微分，获得第i阶次应变模态振型函数在梁结构纵向坐标x位置的函数表达式。

在计算获得N阶次应变模态振型函数后，其矩阵形式{Ψ（x）}1×N可表示为：

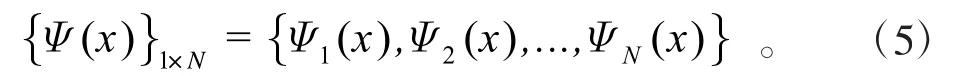
2 数值模拟

为了验证基于位移与应变的转换关系识别梁式桥梁应变模态振型的有效性和准确性，本文对简支梁在噪声随机作用下振动响应进行数值模拟。数值模拟中的简支梁，梁全长为5 m，其梁横断面为工字型，高为0.05 m，梁横断面面积为2.52 cm2，梁横断面惯性矩为10.8 cm4。数值模拟的简支梁沿纵向坐标均匀取21个节点，两节点之间为一单元，共20个单元，每个单元长25 cm。数值模拟的简支梁纵向布置图如图1所示。模拟中对简支梁施加的激励为噪声随机激励，噪声均值为零，标准差为0.25 g（g为重力加速度），激励时间为20 s。

图1 数值模拟简支梁纵向布置图（单位：cm）

由于简支梁振动形式较为简单，其主要振型为前三阶次振型。所以本文数值模拟仅仅考虑简支梁的前三阶次模态振型。为了获取模拟简支梁的前三阶次应变模态振型，利用有限元计算软件，计算出梁底各个节点处动态应变数值，并模拟实际测试采集动态应变数值，如图2所示为梁1/4跨处梁底动态应变数值。

图2 随机激励下1/4跨梁底动态应变

在获取了所有节点梁底的动态应变数据之后，应变模态振型可根据传统的模态参数识别方法获取[1]，获取后作为精确值。对于简支梁来说，其位移模态振型较为简单，可通过结构有限元分析获得。根据位移和应变的相互变换关系，对位移模态振型函数进行两次微分，即得到应变模态振型。其中，梁截面的中性轴在梁高方向上距梁底距离，可根据截面尺寸计算获得。将通过对位移模态振型二次微分计算得到的应变模态振型与精确值进行对比，对比结果如图3所示。

从图3的对比结果可看出，利用位移与应变的转换关系，计算出的简支梁应变模态振型与精确值有着很好的重合度，计算结果精度较高。

图3 简支梁前三阶应变模态振型计算值与精确值对比

梁式桥梁的结构形式主要以简支梁、连续梁居多，接下来本文对连续梁进行数值模拟，继续验证基于位移与应变的转换关系识别梁式桥梁应变模态振型的有效性和准确性。数值模拟中的连续梁，梁全长为10 m，其梁横断面为工字型，高为0.05 m，梁横断面面积为2.52 cm2，梁横断面惯性矩为10.8 cm4。同样，数值模拟的连续梁沿纵向坐标均匀取21个节点，梁被划分为20个单元，每个单元长50 cm。数值模拟的连续梁纵向布置图如图4所示。对连续梁施加的激励同样为噪声随机激励，噪声均值为零，标准差为0.25 g（g为重力加速度），激励时间为20 s。

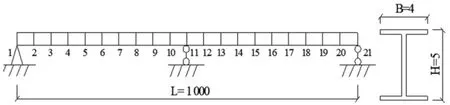
图4 数值模拟连续梁纵向布置示意图（单位：cm）

与简支梁相似，连续梁主要振型同样为前三阶次振型。所以本文数值模拟仅仅考虑连续梁的前三阶次模态振型。为了获取模拟连续梁的前三阶次应变模态振型，利用有限元计算软件，计算出梁底各个节点处动态应变数值，并模拟实际测试采集动态应变数值，梁跨中处梁底动态应变数值如图5所示。

图5 随机激励下跨中梁底动态应变

在获取了所有节点梁底的动态应变数据之后，应变模态振型可根据传统的模态参数识别方法获取[1]，获取后作为精确值。对于连续梁来说，其位移模态振型较为简单，可通过结构有限元分析获得。根据位移和应变的相互变换关系，对位移模态振型函数进行两次微分，即得到应变模态振型。将应变模态振型计算值与精确值进行对比，对比结果如图6所示。

图6 连续梁前三阶应变模态振型计算值与精确值对比

从图6的对比结果可看出，利用位移与应变的转换关系，计算出的连续梁应变模态振型与精确值有着很好的重合度，计算结果精度较高。

3 结束语

本文研究基于位移和应变的转换关系识别梁式桥梁应变模态振型的方法，给出了具体梁结构位移和应变的转换关系公式，及位移模态和应变模态在模态振型上的转换公式。为验证基于位移与应变的转换关系识别梁式桥梁应变模态振型的有效性和准确性，分别对简支梁、连续梁进行了数值模拟，数值模拟结果表明该方法是可行的，并且具有较高的精度。