基于POE建模的工业机器人最优速度规划

吴浩天，黄思，肖湘桂，杨建中

（华中科技大学国家数控系统工程技术研究中心，武汉 430074）

0 引言

工业机器人速度规划[1]分为路径未知和路径已知两种情况，前者主要用于点到点的运动，后者广泛用于焊接、喷涂等工艺上。如何在确定路径的情况下规划机器人的速度使得时间尽可能短成为工业和学术界广泛关注的问题。一类被广泛应用的方法是采用改进遗传算法[2]、改进粒子群算法[3]等进行问题求解，此类算法效率相对较低，很难直接应用到工业生产；还有诸如罚函数法[4]、序列二次规划[5]等方法，其求解精度过分依赖于初始条件，无法保证全局最优。上述方法受制于算法本身存在的缺陷，很难同时保证机器人的运动学和动力学特性。常用来解决此类优化问题的方法还有基于凸优化[6]和可达性分析[7]的最优速度规划；除此之外随着人工智能的发展，神经网络[8]、强化学习[9]等方法也被广泛应用，关键是如何将机器人的运动学和动力学特性充分发挥。

本文未采用传统DH参数法[10]建立机器人运动学模型，而是采用指数乘积公式POE（The Product of Exponentials Formul）[11]，利用其具有一阶连续的良好性质，与李群李代数理论联系起来，方便扩展到动力学建模。在得到机器人全局模型之后，以时间为主要优化目标，综合考虑机器人运动学和动力学约束，基于凸优化理论，将目标问题转化为标准的二阶锥规划[12]模型并完成目标问题的求解，最后仿真结果显示，本文方法在时间上有很大优势，可为工业机器人的实际应用提供理论依据。

1 机器人全局POE运动学分析

以国产华数机器人HSR-605为研究对象，采用指数积建模的方法建立机器人运动学模型，该方法基于指数积公式，将运动方程表示成运动旋量的指数积，由此给出了机器人运动学方程完整几何表达。该方法对比传统DH法，无需建立局部坐标系，大大简化了建模过程，且模型具有更明确的物理和几何意义。下面结合指数积旋量理论针对机械臂正逆运动学进行分析。

HSR-605的指数积建模及尺寸关系如图1所示。

图1 HSR-605机器人连杆坐标系

机器人基座标系{0}的坐标轴方向为X0、Y0、Z0，机器人末端法兰盘坐标系{6}的坐标轴方向为X6、Y6、Z6。L1、L2、L3、L4、L5、L6分别表示机器人指数积建模时各个关节轴线的线矢量，其方向如图2所示，其中L4、L5、L6相交于同一点。a2=360 mm，a3=90 mm，d4=376.5 mm，d6=119 mm。六关节机器人的指数积运动学方程如下：

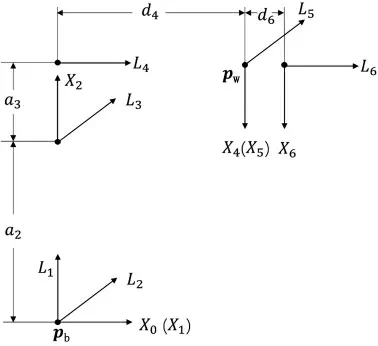
图2 指数积建模及尺寸关系

式中：Li为运动旋量坐标；Li［］为运动旋量；ωi为第i关节旋转轴在基座标系中的轴线方向矢量；ri为第i 关节轴线上的一点在基座标系中的位置坐标。

机器人运动学的正解映射关系如下：

2 时间最优速度规划

本小节首先进行参数化处理，借助弦长参数化理论通过引入路径参数s、s˙、s¨将6n维优化问题转化成相平面s˙-s、s¨-s上的2维问题，大大简化后续的求解过程。根据链式求导法则q˙=q′（s）s˙、q¨=q″（s）s˙2+q′（s）s¨，将关节空间问题转换到参数空间进行求解。

2.1 最优速度规划问题建模

以时间作为主要的优化目标以保证时间最优，且在工业机器人作业的大多数环境当中以牺牲时间效率为代价去节省能量意义不大，故本文并未引入能量项；而考虑到当时间处于最优状态时机器人至少有一个关节轴会处于最大加速度或最大减速度状态，容易产生冲击、抖动等，破坏机械结构，这是由于机器人具有bang-bang特性[14]。故引入冲击项来使规划后的速度相对平缓，且乘上比例因子μ来控制权重。故参数化处理后时间最优速度规划问题的目标函数为

基于第1节POE运动学分析的结论，将机器人关节约束和笛卡尔速度约束考虑在内。其中关节约束主要考虑电动机的性能上限，使每个关节轴均不会超速；由于工业机器人在焊接、喷涂等领域作业时更多关注的是末端TCP的工作状态，故此处引入TCP笛卡尔速度约束。运动学约束为：

2.2 凸优化问题求解

在得到时间最优速度规划问题的目标函数和约束条件后，基于凸优化理论进行问题的分析和求解。如式（5）～式（7）所示，为实现将非线性目标问题线性化，且引入仿射函数作为约束来进行凸优化分析，本文将参数速率b（s）=s˙2和参数加速率a（s）=s¨作为优化目标，根据不等式约束，将τi（s）用动力学方程（7）代替后，可以简单画出此优化问题在相平面上的可行域，如图3所示。

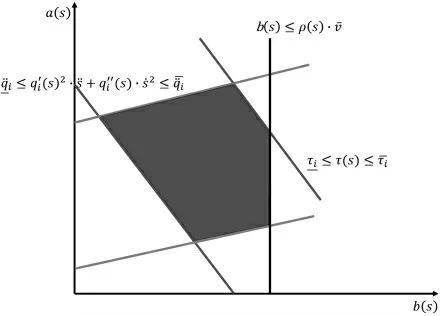
图3 不等式约束可行域分析

根据路径参数方程对路径参数s进行等误差离散成k份，在转矩约束中参数均取为区间平均值，且根据参数速率和参数加速率之间的关系，动力学方程经过一系列变换后离散化目标凸优化问题如下：

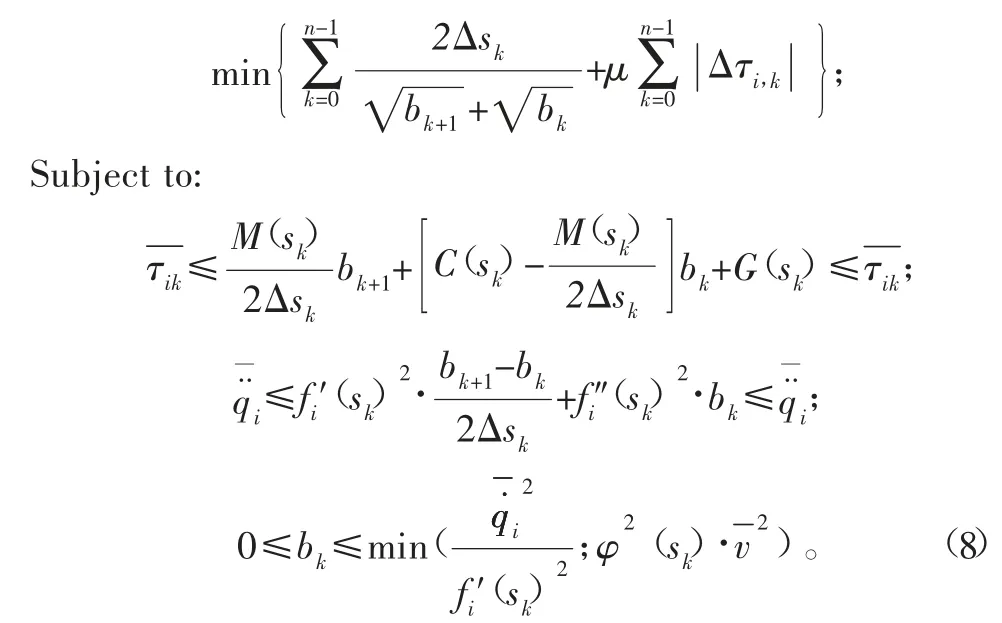
上述优化问题的优化变量为离散后的参数速率b（s），考虑到目前已有如SEDUMI[15]、YILMIP[16]等非常成熟的标准二阶锥规划库来求解此类优化问题，故仿真部分基于凸优化子问题，二阶锥规划来进行求解。

3 仿真结果与分析

借助SEDUMI标准工具包进行二阶锥问题求解，最终得到的是各个离散点对应的关节角位置、关节角速度及关节角加速度。利用机器人离线编程软件InteRobot生成图4所示的路径，将弦高误差设为0.01 mm，根据等误差离散后的结果，可得到312个路径点。

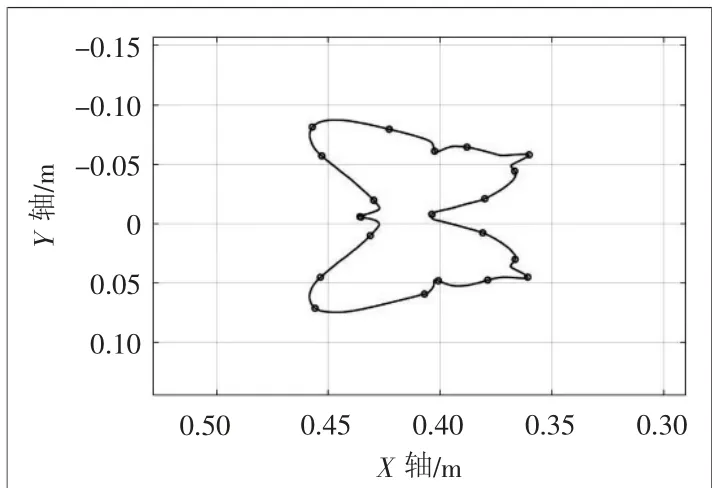
图4 离线生成路径曲线

根据第一节所述机器人POE逆运动学计算各关节位置信息。机器人现有的插补算法下规划结果和优化后仿真结果如图5～图6所示。

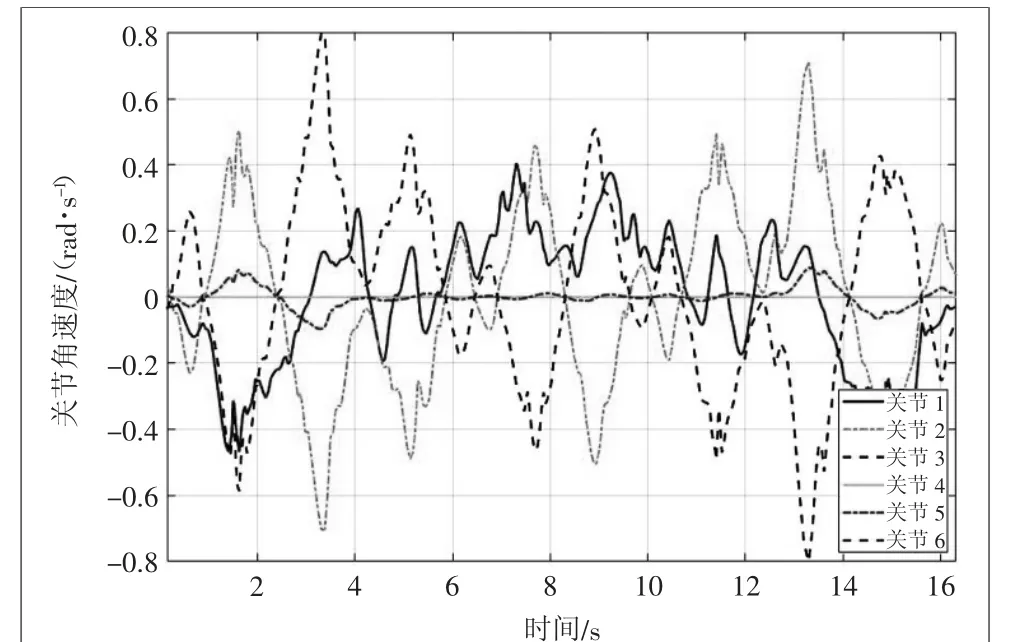
图5 机器人原有的规划算法下关节角速度

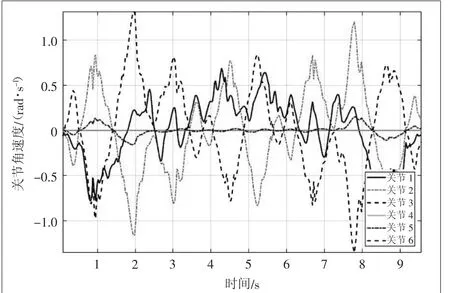
图6 优化后关节角速度

根据优化前后关节角速度对比曲线可知，从时间上来说，优化后的关节角速度与原有的规划算法下关节角速度相比运行时间更短，且抖动有明显好转。

下面对冲击项的比例系数进行合适的选取（如表1），若单纯考虑时间最优运行时间为3.5 s，但此时有一个关节轴会处于最大加速状态，比较μ=0和μ=0.1两个状态下的参数加速率a（s）值如图7所示，能看出合适选取冲击项的比例系数能对加速度突变有明显改善。实验结果表明，当μ=0.1时机器人会处于一个关节抖动相对理想的最大化效率运行状态。

表1 最优速度规划时间结果对比 s

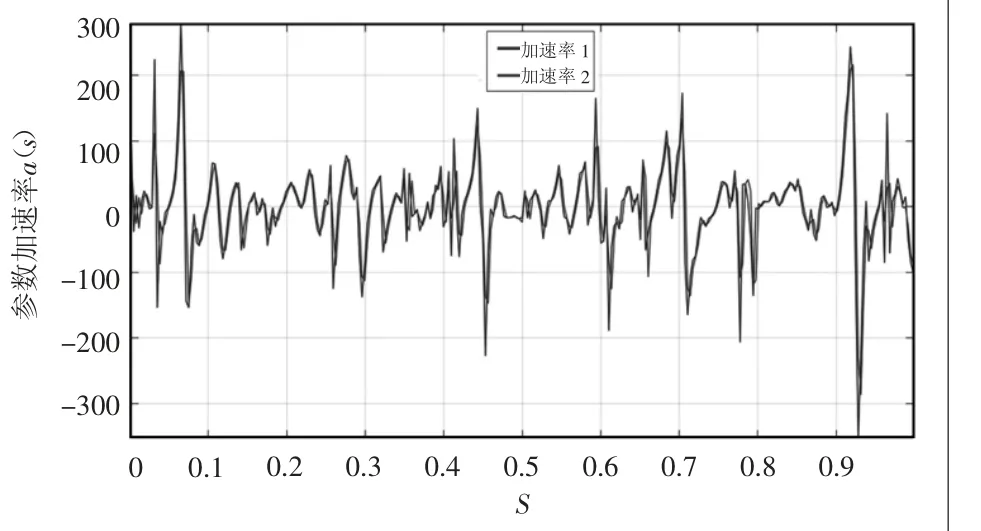
图7 μ=0、0.1下的参数加速率a（s）值

4 结论

通过指数积建模的方法建立机器人运动学模型，提升准确性的同时保证了计算效率，且综合考虑机器人的运动学、动力学约束，解决给定路径下机器人的时间最优速度规划问题。仿真结果表明，与华数机器人现有的插补算法对比，该方法在缩短原有算法运行时间的基础上减少了关节抖动。此方法可为工业机器人在喷涂、打磨等领域的应用提供理论基础。