基于fgoalattain函数的齿轮传动多目标优化设计

王纯， 韩加好，张燕， 卢建国

（连云港职业技术学院，江苏 连云港 222000）

0 引言

齿轮传动因其具有传动效率高、可靠性高等优点，被广泛应用在机械设备的传动系统中，随着工业的发展，机械结构向着大型化、复杂化方向发展，采用传统优化设计方法设计出来的结构综合性能一般不能达到理想状态，很难满足优化设计要求。为解决以上问题，本文以二级斜齿圆柱齿轮传动系统作为研究对象，运用最优化理论和方法，建立齿轮传动多目标优化模型，并采用Matlab优化工具箱（Optimization Tool）提供的函数fgoalattain进行参数优化计算，其计算结果为多目标齿轮传动优化设计提供一定的参考[1-5]。

1 多目标优化数学模型

1.1 多目标优化设计模型设计变量的选取

对于图1所示的二级齿轮传动系统来说，涉及到很多的设计参数及影响因素，为了简化问题，我们将设计的主要参数作为优化设计变量：

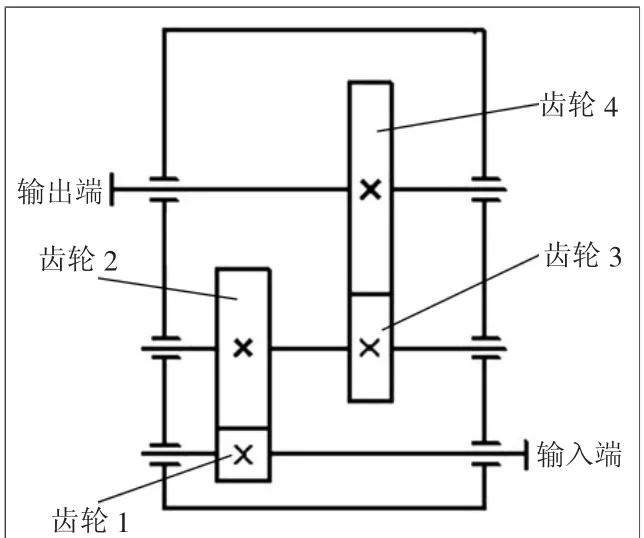
图1 二级齿轮传动系统示意图

式中：mn1、mn2分别为高、低速级齿轮法向模数，mm；z1、z2分别为高、低速级的小齿轮齿数；i1为高速级传动比；β1、β3分别为斜齿轮的螺旋角，（°）。

1.2 多目标优化模型目标函数的确定

1.2.1 二级齿轮传动系统体积

1.2.2 二级齿轮传动系统重合度

对两级齿轮传动系统来说，重合度具有更重要的意义，重合度越大，传动越平稳。我们将啮合齿轮的重合度的相反数作为第二个优化目标，即目标函数[7]为

1.3 多目标优化模型约束函数的确定

约束条件主要分为几何和性能两种约束。几何约束一般有齿数约束、模数约束、齿宽系数等；性能约束一般包括齿轮齿面接触疲劳强度约束、齿根弯曲疲劳强度约束[8-12]。

1.3.1 几何约束

1）齿数约束。根切现象的产生是因为用展开法加工渐开线齿轮时，被加工齿轮的齿数过少，切削刃把齿轮的根部已展成出的渐开线切去一部分。因此，要避免根切，必须是刀具的齿顶线不超过啮合极限点。综合考虑传动效果和结构尺寸的合理性等因素。因此，齿数z取值范围为

1.3.2 性能约束

1）齿面接触疲劳强度约束。根据齿轮的齿面接触疲劳强度校核公式σH≤［σH］，得：

式中：YFa为齿形系数；YSa为应力修正系数；Yβ为螺旋角影响系数；［σF］为许用弯曲应力。

1.4 多目标优化函数—fgoalattain函数

函数fgoalattain是基于序列二次规划法（SQP）的一种求解非线性约束优化问题的函数，其适用于求多变量有约束非线性的最小值问题。其常用的调用格式为

2 计算实例及结果分析

2.1 已知条件

以某二级斜齿减速器为例，输入功率为7.4 kW，转速为1450 r/min，总传动比i=25.9。齿轮材料及热处理为：大齿轮选用45钢，其硬度为240 HBS；小齿轮选用45Cr钢，其硬度为260 HBS；每天工作12 h，使用寿命为10 a，希望节省材料。

2.2 确定参数

2.3 建立约束条件

根据式（4）～式（12）建立15个约束条件：

2.4 优化求解

本实例是多目标约束优化问题，可选用Matlab优化工具箱中用于求解约束优化问题的fgoalattain函数进行求解。函数fgoalattain是基于序列二次规划法（SQP）的一种求解多变量非线性约束优化问题的函数。根据设计要求及经验确定初值、目标值、权重系数及变量上下界：

X0＝［2，2，18，18，5.32，15，15］；goal＝［4×106，－4］；

weight＝［4×106，－4］；Ub＝［3，4，19，19，5.47，20，20］；Lb＝［2，2，16，16，5.05，8，8］。

2.5 优化结果分析

采用fgoalattain函数对本实例中的齿轮传动系统数学模型进行求解，并对优化结果圆整，得到优化结果，如表1所示。

根据表1齿轮优化前后数值的对比可知：齿轮传动系统体积从4.2×106mm3减小到2.81×106mm3，体积减小了33.1%，优化效果明显。同时，齿轮重合度从5.15 增 大 到5.20，增 加了0.97%。优化结果表明，fgoalattain函数对该齿轮传动系统优化结果合理，效果明显。

表1 优化前后参数对比

3 结论

本文通过分析，得到了二级斜齿圆柱齿轮传动系统优化设计的目标函数及约束条件，确立了该系统的设计变量，建立二级斜齿轮传动的多目标优化模型，并将该模型应用到工程实际中，对该齿轮传动系统进行合理优化。由优化结果可知，该设计满足要求，同时节约材料，降低制造成本。