仿人体外骨骼髋关节并联机构位置及仿真分析

谢哲东， 张煜， 陈晨， 李斌， 朱俊昊

（吉林农业大学 工程技术学院，长春 130118）

0引言

随着机械自动化技术和微型计算机技术的不断发展和进步，基于人体仿生学和人机工程学所建立的外骨骼机器人有了较大的突破。其中助力型外骨骼机器人在野外军事、灾难救援和农业劳作等应用中越来越广泛[1-2]。部分地区农作物不适合机器运输，同时人工的劳作强度太大，此时农用下肢助力外骨骼机器人的出现减少了穿戴者劳动负荷，提升了运输效率[3]。

下肢助力外骨骼机器人的髋关节是主要的传力关节。当人体负重时，其重力通过髋关节传递到足底。目前，下肢助力外骨骼机器人的髋关节多数没有驱动或仅有一个电动机驱动，如任星宇等[4]针对农用下肢外骨骼运动学分析的旋量解法文中提出的农用下肢外骨骼机器人，其缺点是当负重后人体髋部的驱动力增加，人需要适应环境维持平衡；同时其设计多为连杆机构，当运动需求较多时，其结构较复杂、工作效率降低、构件产生的惯性力较难平衡，所以有众多的学者对髋关节机构进行了深入研究。侯雨雷等[5]提出可应用于人形机器人髋关节的3-RRR+（S-P）球面并联机构。程刚等[6]对3SPS+1PS并联机构的设计和控制进行了分析，对机构的工作空间进行了优化。王松涛等[7-8]对3SPS+1PS并联髋关节试验机分岔行为和尺度进行了分析。以上并联机构并不适用于下肢外骨骼机器人的髋关节。因此本论文针对下肢外骨骼机器人行走过程中的髋关节机构角度变化的设计要求，通过对人体髋部的骨骼和肌肉的分析，并结合少自由度并联机构特点设计出下肢外骨骼机器人髋关节并联机构。该机构结构简单、易于控制、占用空间小。

1 外骨骼机器人髋部机构

通过对国内外下肢外骨骼的研究，结合人体骨骼形状、肌肉分布、筋的分布及外骨骼机器人的设计需求[9-11]，设计一款下肢助力外骨骼机器人，由上体机构、髋部机构、大腿机构、膝部机构、小腿机构和足踝机构构成，如图1所示。提出一种用于下肢助力外骨骼机器人的髋关节机构，如图2、图3所示。

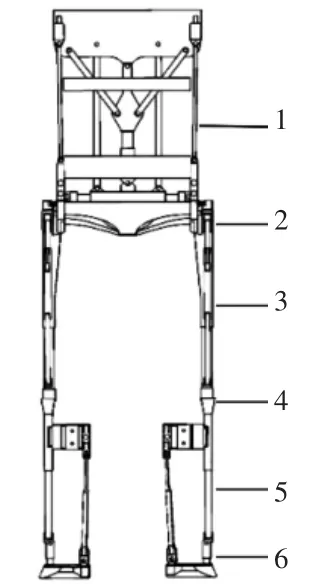
图1 外骨骼机器人

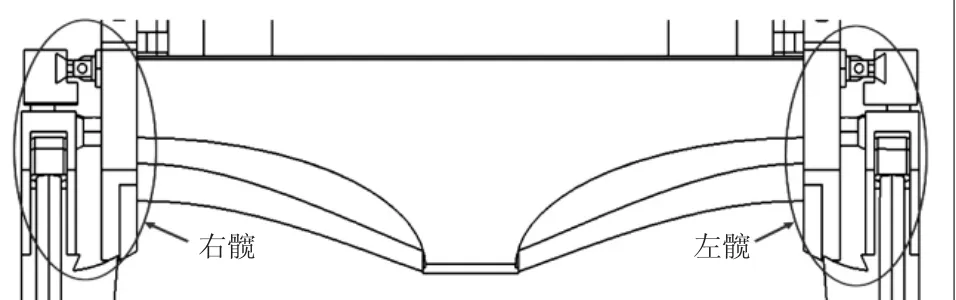
图2 髋部机构主视图

图3 髋部机构左视图

外骨骼机器人髋关节机构由静平台、动平台1、动平台2、2个相同的PRRP支链、1个球支链构成，如图4所示。其中PRRP支链由滑块、连接十字节、活塞杆构成。如图5所示，PRRP支链的一端通过滑块与动平台1相连，另一端通过活塞杆与静平台相连。动平台1与动平台2通过滑槽相连。球支链一端固定连接在静平台上，另一端通过球支链上的球副与动平台2相连。2个PRRP支链到球支链的距离相同，通过调节2个PRRP支链中活塞杆的伸长量来控制动平台的运动，从而实现髋关节机构的内旋外旋、外展内收。

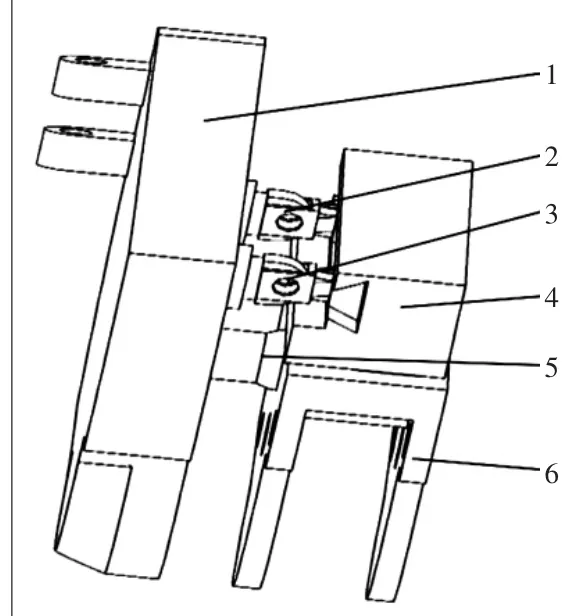
图4 髋关节机构结构图

图5 PRRP 支链结构图

2 髋关节并联机构及坐标系建立

并联机构是指动平台和定平台通过至少2个独立的运动链，机构具有至少2个或2个以上自由度，且以并联方式驱动的一种闭环机构[12]。髋关节机构完全符合并联机构定义。通常并联机构的动平台只有1个，而髋关节机构动平台是由2部分构成，由于2个动平台之间是由滑槽连接，所以与1个动平台中开滑槽的效果一样，所以髋关节机构为并联机构。

通过对髋关节并联机构分析，建立机构的位置分析模型，如图6所示。在平面ABC建立参考坐标系O-XYZ，即在静平台建立参考坐标系O-XYZ，其中O点位于AB连线的中点，X轴与AB共线并由O点指向B，Z轴垂直于ABC所确定的平面，Y轴方向通过右手定则确定。在动平台1上建立坐标系M-X1Y1Z1，即在平面P4P5P1上建立坐标系M-X1Y1Z1，其中M点位于P4P5连线的中点，X1轴与P4P5共线并由M指向P5，Z1轴垂直于P4P5S所确定的平面，Y1轴方向通过右手定则确定。其中SP1为动平台2，动平台2通过P1与动平台1相连。

3 髋关节并联机构自由度分析

运用螺旋理论对髋关节并联机构进行自由度分析。由于螺旋的相逆性和相关性与坐标的选择无关[13]，所以采用图6坐标系进行分析。螺旋坐标中ai、bi、ci与机构的尺寸和轴线的位置有关，在自由度分析时不用求出具体值。由于髋关节并联机构的2条PRRP支链相同，所以分析1条PRRP支链和球支链。球支链是由球副和2个动平台之间的滑槽组成。X轴正向PRRP支链的运动螺旋系为：

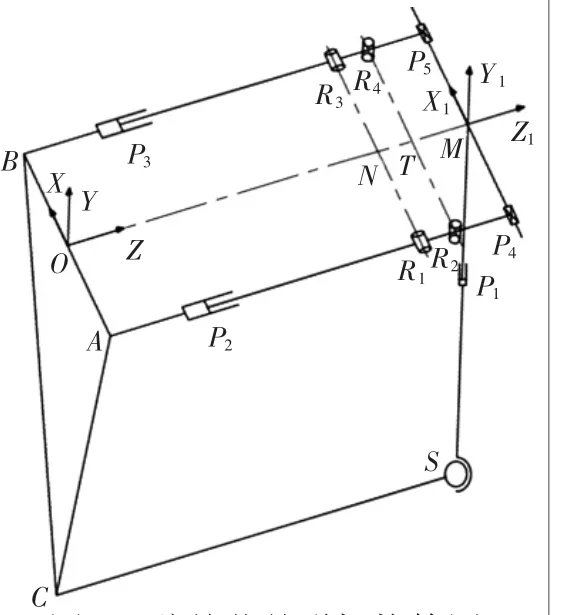
图6 髋关节并联机构简图

3个分支施加给平台3个约束螺旋，构成动平台的约束螺旋系，对其求反螺旋可得：

4 髋关节并联机构位置分析

位置分析是找出主动关节的位移和末端执行器的姿态之间的运动学关系[14]。如图6所示，通过对机构的分析，得出PRRP支链旋转副R2、R4始终在R1R3P5P4平面内，PRRP支链中2个旋转副的旋转角度相同，旋转副R1、R3旋转的角度与动平台绕X轴旋转的角度一致，旋转副R2、R4旋转的角度与动平台绕Y轴旋转的角度一致。取转向相同的旋转副连线的中点，分别为T、N。线段TN与PRRP支链2个旋转副连线平行。

取PRRP支链AP4为支链1，PRRP支链BP5为支链2，球支链为支链3。初始状态下，动平台与静平台平行，则AR1=BR3=l，2个旋转副轴线的距离为R1R2=R3R4=TN=l1，动平台到旋转副的距离为R2P4=R4P5=MT=l2，AB的长度为l3，OC的长度为l4。动平台绕X轴旋转的角度α和动平台绕Y轴旋转的角度β的示意图如图7所示。

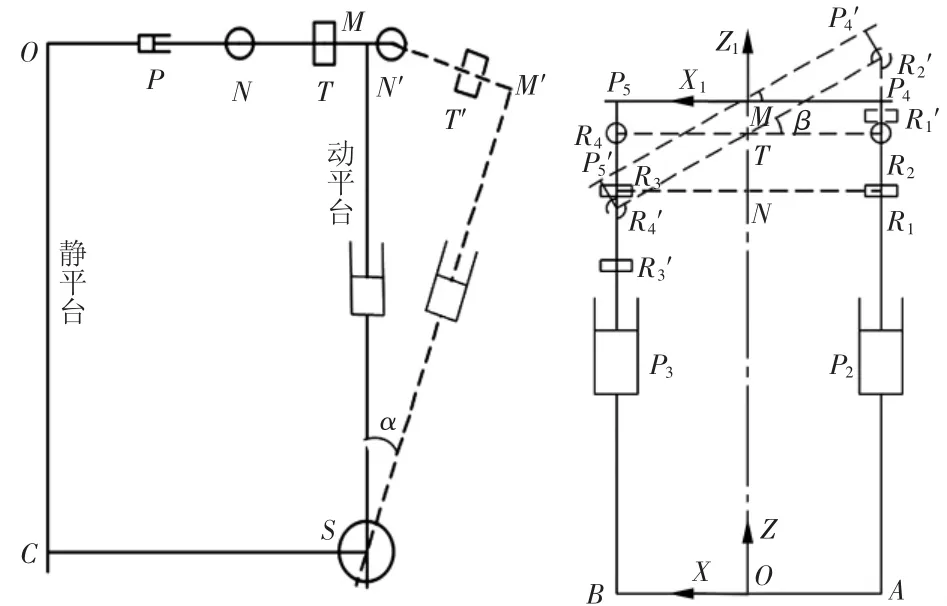
图7 动平台绕X、Y 轴旋转示意图

4.1 位置逆解

位置逆解是当髋关节并联机构的机构参数、平台绕X的旋转角度α和动平台绕Y的旋转角度β已知，求解PRRP支链中P副的移动距离Δli。

根据以上分析，通过几何关系可求解出M点在定坐标的位置矢量，即动坐标系原点在定坐标系中的坐标。

利用几何关系可得平移副P4、P5在动平台坐标系中的位置矢量：

PRRP支链中P副的移动方向为Z轴，通过几何关系得到P副的移动距离为：

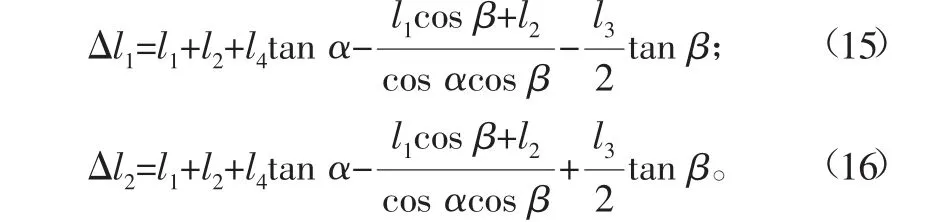
通过对式（15）、式（16）分析可得α角的变化不会影响β角的变化，β角的变化会影响α角的变化。

4.2 位置正解

位置正解是当髋关节并联机构的结构参数和PRRP支链中P副的移动距离Δli已知，求解动平台绕X的旋转角度α和动平台绕Y的旋转角度β。

采用图6坐标系，由于机构为三自由度并联机构，机构相对简单，采用数值法对机构进行位置正解分析。从动坐标系M- X1Y1Z1到定坐标系O-XYZ的变换矩阵为

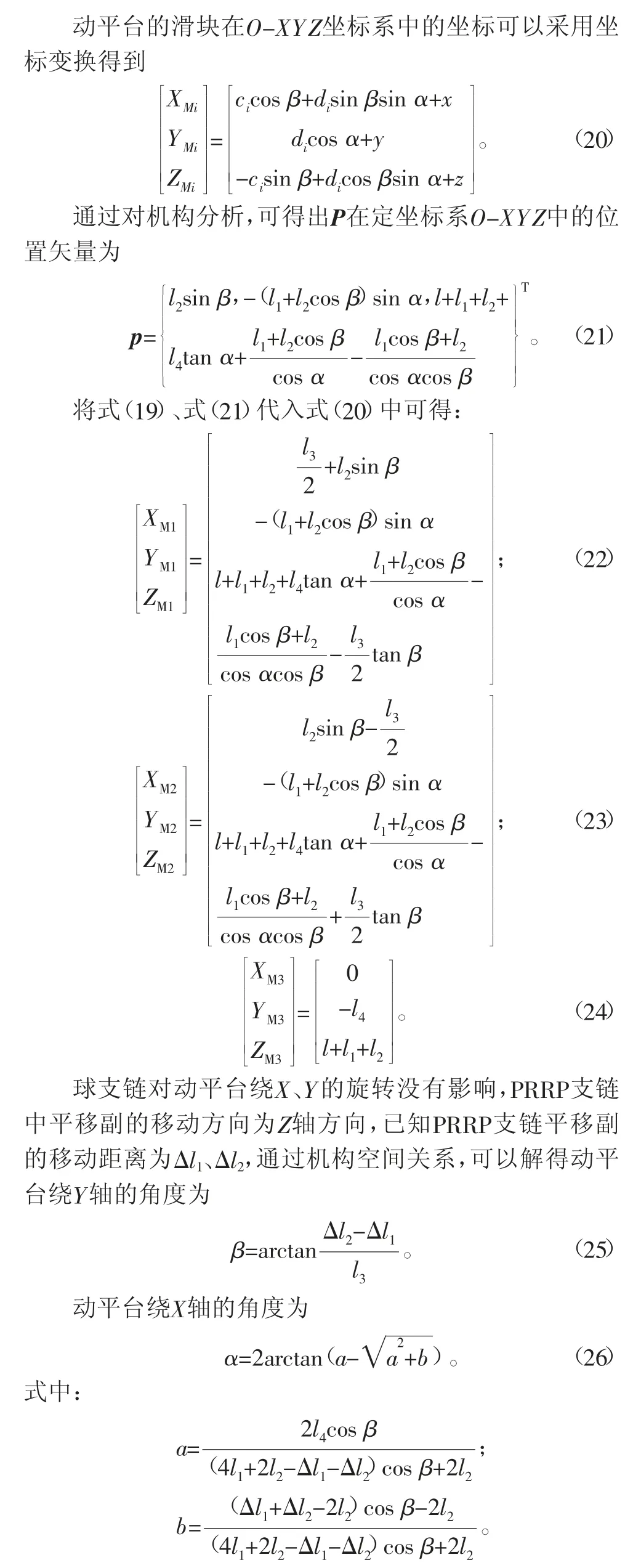
5 髋关节机构位置仿真分析

5.1 仿真分析

将建立的髋关节并联机构三维模型导入ADAMS中，对导入模型的零件进行材料设置和约束[15]。初始状态下，动平台与静平台平行，通过对2个支链施加驱动函数，得到动平台在3种情况下绕X、Y轴旋转角度变化。

1）情况1。初始状态下，动平台仅绕X旋转，支链1和支 链2 活 塞 杆 施 加 的 驱 动 都 为st ep （time，0，0，0.5，－4.6*time）+step（time，0.5，0，1，23.2*（time－0.5）），得到动平台随时间仅绕X轴的旋转角度，如图8所示。

图8 动平台随时间仅绕X 轴的旋转角变化图

通过对图8的分析得出，在状态1情况下，支链1的旋转副R1和支链2的旋转副R3旋转的角度与支链3的球副S绕X轴旋转的角度一致，证明上文对机构的分析正确。动平台绕X轴旋转的角度范围为-13°～4.6°。

2）情况2。初始状态下，动平台仅绕Y旋转，支链1活塞杆施加的驱动为step（time，0，0，0.5，4.6*time）+step（time，0.5，0，1，－13.8*（time－0.5）），支链2活塞杆施加的驱 动 为：step （time，0，0，0.5，－4.6*time）+step（time，0.5，0，1，+13.8*（time－0.5））。得到动平台随时间仅绕Y轴的旋转角度，如图9所示。

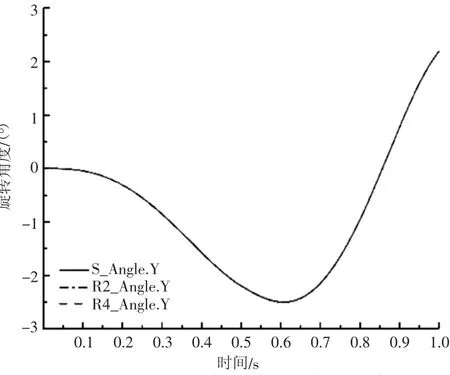
图9 动平台随时间仅绕Y 轴的旋转角度变化图

通过对图9的分析得出，在状态2情况下，支链1的旋转副R2和支链2的旋转度R4旋转的角度与支链3的球副S绕Y轴旋转的角度一致，证明上文对机构的分析正确。此时绕Y轴旋转的角度范围为-2.5°～2.3°。

3）情况3。初始状态下，动平台先绕X轴旋转，然后绕Y轴旋转。如图10和图11所示，在0～0.5 s时，支链1、2在同方向伸长相同位移，S1、S2、S3同方向位移的长度不同。曲线S1、S2在0.5～1.0 s时，支链1、2在相反方向进行同长度的位移。为防止动平台与静平台碰撞，曲线S3在0.5～1.0 s时，支链1、2在相反方向进行不同长度的位移。得到动平台随时间绕X、Y轴的旋转角度变化。

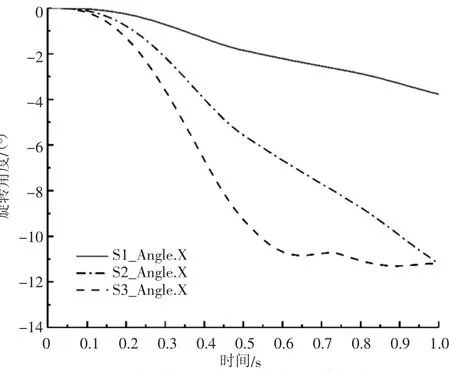
图10 动平台随时间绕X 轴的旋转角变化图

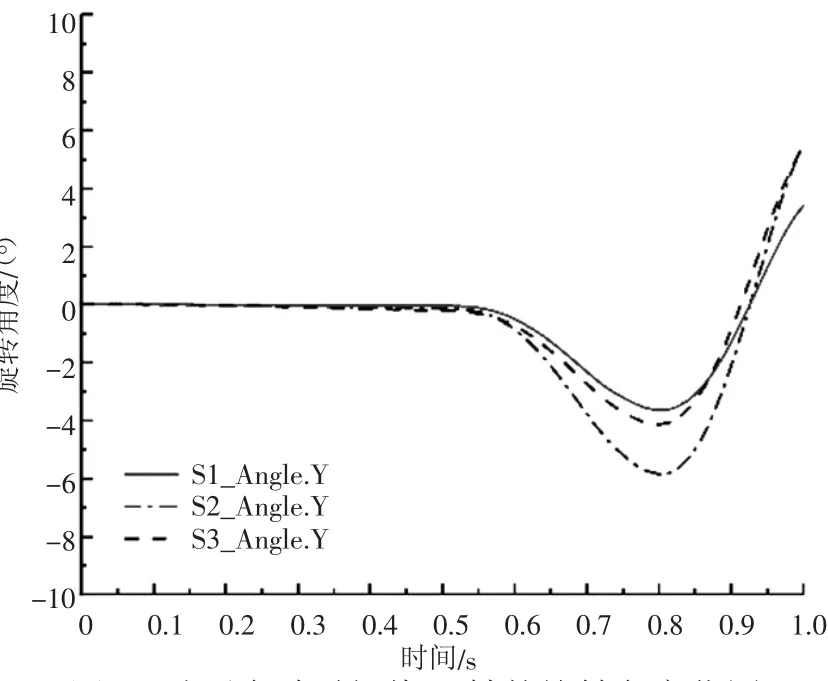
图11 动平台随时间绕Y 轴的旋转角变化图

对图10、图11的S1分析可得，当动平台绕Y轴旋转，即在0.5～1.0 s时，动平台绕Y轴的旋转会影响绕X轴旋转角度。对图10、图11的S1、S2、S3分析可得，当动平台绕X轴旋转，即当时间为0～0.5 s时，动平台绕Y轴的旋转角度大约为绕X轴旋转角度的2%。忽略2%的误差，仿真的结果与位置逆解的结果一致，即动平台绕X轴的旋转不会影响绕Y轴的旋转，动平台绕Y轴的旋转会影响绕X轴的旋转。在0.5 s时，图10中随着S1、S2、S3动平台绕X旋转角度的增大，图11中在0.5～1.0 s动平台绕Y轴的旋转的角度变化范围是由小到大再到小。

图6中髋关节机构坐标系X、Z轴和运动仿真坐标系X、Z轴的方向相反，所以髋关节并联机构外展内收运动的角度变化范围为-4.6°～13°，内旋外旋运动的角度随外展内收运动的角度变化，其极值变化范围为-6.3°～5°。髋关节并联机构角度变化范围与人体髋关节角度变化范围对比如表1所示。

表1 运动角度变化范围对比表

由表1可以得出人在行走过程中髋关节内旋外旋的角度范围为-2°～3°，外展内收的角度范围为-6°～4°。人行走过程中步角的大小仅与髋关节内旋外旋运动有关，人行走过程中，为保证站立稳定，髋关节内收的角度越大外旋的角度越大。所以髋关节并联机构的角度范围可以满足穿戴者在正常行走过程中的角度变化。

5.2 算例分析

根据计算需求，将模型的2个驱动分别定义为2*time和13*time。得到动平台随时间绕X轴的旋转角度和动平台随时间绕Y轴的旋转角度，如图12、图13所示。

图12 动平台随时间绕X 轴的旋转角度变化图

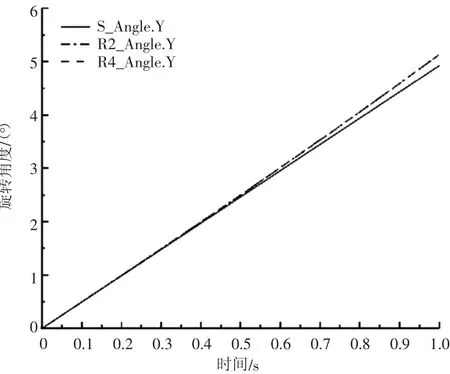
图13 动平台随时间绕Y 轴的旋转角度变化图

用MATLAB对髋关节并联机构进行位置正运动学分析，将不同时间得到活塞杆的驱动长度代入式（26）、式（27）中，得到动平台绕X、Y轴的角度值，如表2所示。将表2中的数据通过MATLAB拟合得到曲线，如图14、图15所示。

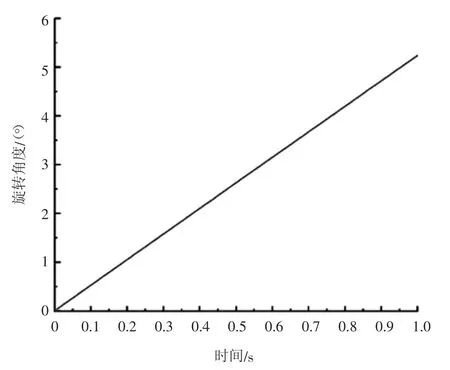
图15 动平台随时间绕Y 轴的旋转角度变化图

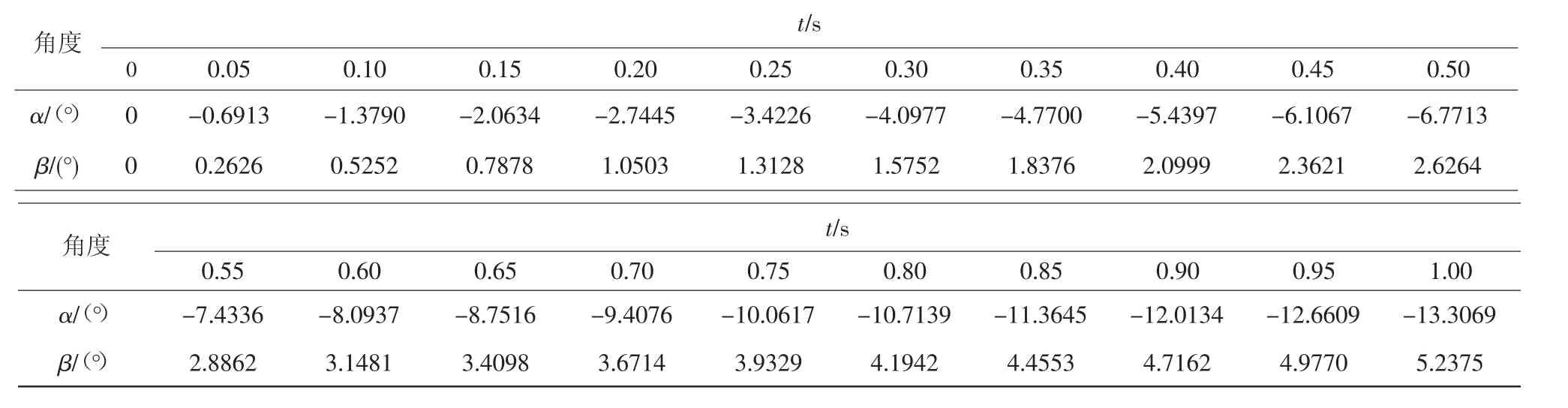
表2 动平台随时间绕X、Y轴的角度值

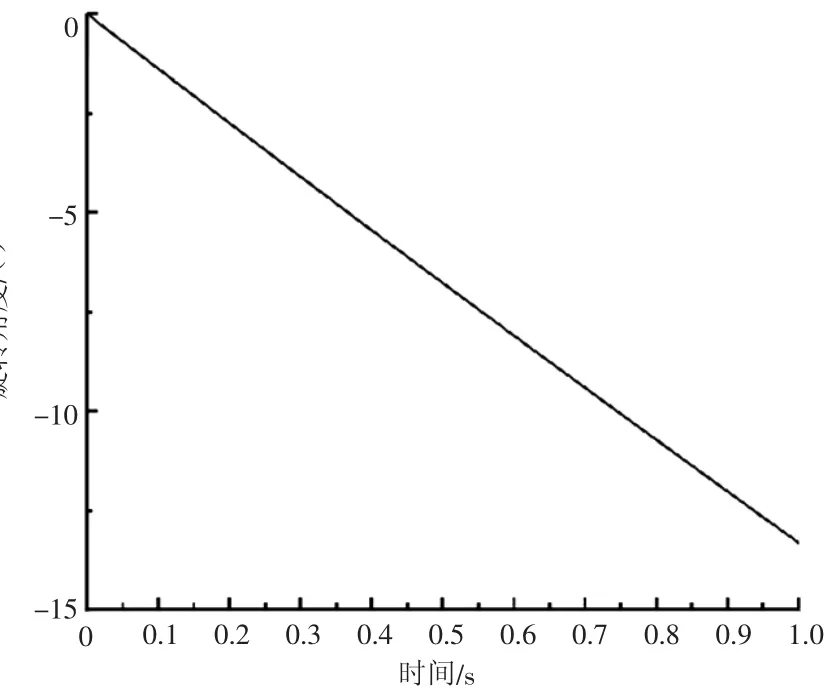
图14 动平台随时间绕X 轴的旋转角度变化图

图12中旋转副R1、R3的旋转角度一致，与球副S的旋转角度有2%的误差。图13中R2、R4的旋转角度一致，与球副S的旋转角度有2%误差。在对比图12和图14，以及图13和图15，MATLAB得到的计算结果与ADAMS仿真得到的结果的偏差为2%左右。由于偏差较小，可以认为仿真结果与计算结果一致。

5.3 偏差分析

模型导入后，零件的坐标与ADAMS系统默认的坐标存在小角度的偏差，从而造成仿真与计算形成偏差。

在模型约束时，在零件中创建Marker点，部分Marker点的创建需通过几个Marker点的坐标计算得到，在选取Marker点时会出现偏差，计算得到的Marker点会将选取的偏差累计，从而造成仿真与计算形成偏差。

6 结论

通过对髋关节并联机构分析，得到以下结论。

1）基于螺旋理论对髋关节并联机构的3个自由度和位置进行了分析，结果表明髋关节并联机构运动合理、结构简单、易于控制。

2）运用ADAMS对髋关节并联机构进行仿真分析，髋关节并联机构运动外展内收-4.6°～13°及内旋外旋-6.3°～5°的运动角度变化符合人体正常行走过程中髋关节角度外展内收-6°～4°及内旋外旋-2°～3°的运动角度变化。证明髋部并联机构的合理性和可行性，同时髋关节运动角度范围为踝足关节的设计打下基础。

3）用MATLAB对髋部机构进行了算例分析，算例分析结果绕X、Y的角度0°～-13.3069°和0°～5.2375°与仿真结果绕X、Y的角度0°～-13.573°和0°～5.343°基本一致，证明仿真和计算的正确性。