耦合变分包含系统解的存在性
2022-06-21熊益英何家洪
熊益英, 何家洪
(北部湾大学 理学院,广西 钦州 535011)
0 引言
在文献[1-7]中引入一类耦合变分包含系统问题,求解(x0,y0)∈H1×H2,使得
(1)
其中,H1,H2为实Hilbert空间,F1∶H1→2H1;F2∶H2→2H2为给定的非空集值映射,f1∶H1×H2→H1;f2∶H1×H2→H2为给定的非空单值映射。
该问题的求解有以下几种特别的情形:
(a)如果H1=H2=H,η∶H×H→H,F1(x)=Δηg1(x),F2(y)=Δηg2(y),其中,Δηg1(·)和Δηg2(·)分别表示真η-次可微泛函g1∶H→∪{+∞}和g2∶H→∪{+∞}的η-次微分映射(参见文献[8]),那么问题(1)变为:求解(x0,y0)∈H×H,使得
(2)
问题(2)称为非线性似变分不等式系统问题。
(b)如果F1(x)=∂g1(x),F2(y)=∂g2(y),其中,∂g1(·)和∂g2(·)分别表示真凸下半连续泛函g1∶H1→∪{+∞}和g2∶H2→∪{+∞}的次微分映射,那么该问题退化为:求解(x0,y0)∈H1×H2,使得
(3)
问题(3)称为非线性变分不等式系统问题。文献[9-10]研究了该问题。
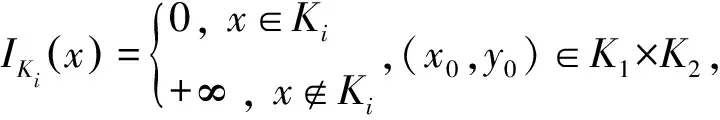
(4)
其中,K1,K2分别为H1,H2中的非空凸闭集。文献[11-12]研究了该问题。
(e)如果H1=H2=H,f1(x,y)=-g(x,y),f2(y,x)=-g(y,x),F1(x)=G(x),F2(y)=G(y),问题(4)退化为:求解(x0,y0)∈H×H,使得
g(x0,y0)∈G(x0),g(y0,x0)∈G(y0)。
(5)
由于G为多值映射,问题(5)也称为多值耦合重合点问题。特别地,如果G(x)={φ(x)},问题(5)退化为:求解(x0,y0)∈H×H,使得
g(x0,y0)=φ(x0),g(y0,x0)=φ(y0)。
(6)
问题(6)也称为耦合重合点问题。文献[13]证明了它的解存在。如果φ是恒等映射,问题(6)退化为:存在(x0,y0)∈H×H,使得
g(x0,y0)=x0,g(y0,x0)=y0。
(7)
问题(7)也称为耦合不动点问题。文献[14]证明了它的解存在。
本文主要研究在赋范线性空间中,问题(1)的解的存在性及其相关问题。在文献[5-6]研究的问题中,集值映射要求的条件非常强,且并未给出实例,很难找到满足条件的映射。因此,本文在文献[5-6]的基础上,将集值凸映射的条件去掉,适当加强单值映射条件,利用KKM引理来研究问题(1),改进了文献[5-6]的研究结果。
1 预备知识
设X为赋范空间,对任意的集合A,B⊆X,定义αA+βB={αa+βb|a∈A,b∈B},α,β∈和本文在集合上定义的‖·‖并非范数,而是一个记号,它具有如下的性质:(i)A⊂B⟹‖B‖≤‖A‖;(ii)‖A+B‖≤‖A‖+‖B‖。
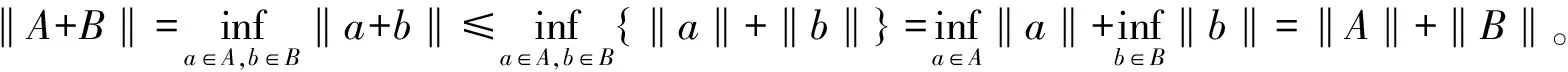
注1.1 ‖A-B‖≤‖A‖-‖B‖不成立,例如:X=,A=[1,2],B=[3,4],‖A‖=1,‖B‖=3,‖A‖-‖B‖=1-3=-2。另一方面,‖A-B‖=‖[-3,-1]‖=1,因此,‖A-B‖≤‖A‖-‖B‖不成立。
定义1.1[15]设X为赋范空间,A,B⊂X,A与B的Hausdorff度量H(·,·)定义如下:
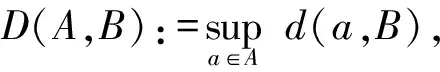
定义1.2[16]设X为赋范空间,{Bn}为X中的非空集合序列,称{Bn}在Hausdorff度量下收敛于B,当且仅当H(Bn,B)→0。
定义1.3[17]设X是赋范空间,K和U是X中的非空凸集,f:K×K→X。如果对任意的(x,y),(x1,y1)∈K×K,λ∈[0,1],u∈X,有
‖f(λ(x,y)+(1-λ)(x1,y1)-u‖≤max{‖f(x,y)-u‖,‖f(x1,y1)-u‖},
则称f是几乎拟凸映射。
定义1.4[17]设X,Y为拓扑空间,集值映射F:X→2Y,x0∈X。若对包含F(x0)的任一开集U,存在x0的邻域V,使得F(V)⊂U,则称F在x0处上半连续。F在每一点x处上半连续,则称F为X上的上半连续映射。
定义1.5[17]设X,Y为拓扑空间,集值映射F:X→2Y,x0∈X。若对任意的y∈F(x0)和对X中收敛于x0的一个网{xn,n∈+},存在网{yn,n∈+}满足对任意的n∈+,yn∈F(xn),且{yn}收敛于y,则称F在x0处下半连续。F在每一点x处下半连续,则称F为X上的下半连续映射。
定义1.6[17]设X,Y为拓扑空间,集值映射F:X→2Y。对任意的x∈X,若F在x处既上半连续又下半连续,则称F在x处是连续的,若F在x中的任一点都连续,称F在X上连续映射。
定义1.7[17]设X,Y为拓扑空间,非空集值映射F:X→2Y,若对任意的x∈X,F(x)为闭集(凸、有界、紧等)集,则称F为闭值(凸值、有界值、紧值等)映射。

引理1.1[18]设X,Y为拓扑空间,F:X→2Y为紧值映射,那么F是连续映射,当且仅当F在Hausdorff度量下连续。




定理1.2 设X是赋范空间,K是X中的非空凸集,U⊂X,如果f:K×K→X为几乎拟凸映射,则对任意的(x1,y1),(x,y)∈K×K,λ∈[0,1],有
‖f(λ(x,y)+(1-λ)(x1,y1))+U‖≤max{‖f(x,y)+U‖,‖f(x1,y1)+U‖}。
证明:由f为几乎拟凸映射,(x1,y1),(x,y)∈K×K,λ∈[0,1],u∈X,有
‖f(λ(x,y)+(1-λ)(x1,y1))-u‖≤max{‖f(x,y)-u‖,‖f(x1,y1)-u‖},
由于-u∈X,故‖f(λ(x,y)+(1-λ)(x1,y1))+u‖≤max{‖f(x,y)+u‖,‖f(x1,y1)+u‖}。

当max{‖f(x,y)+u‖,‖f(x1,y1)+u‖}=‖f(x,y)+u‖时,两边分别取下确界,则有‖f(λ(x,y)+(1-λ)(x1,y1))+U‖≤‖f(x,y)+U‖。
同理,则有‖f(λ(x,y)+(1-λ)(x1,y1))+U‖≤‖f(x1,y1)+U‖。因此,‖f(λ(x,y)+(1-λ)(x1,y1))+U‖≤max{‖f(x,y)+U‖,‖f(x1,y1)+U‖},故定理1.2成立。

证明:由定理1.1和定理1.2可得推论1.1成立。
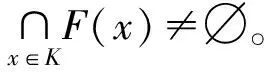
2 主要结论
定理2.1 设X为赋范空间,K是X中的非空凸紧集,fi:K×K→X为连续、几乎拟凸映射,Fi:K→2X是连续、紧值映射,i=1,2,则存在(x0,y0)∈K×K,使得

证明:定义集值映射G:K×K→2K×K,对任意的(u,v)∈K×K,
G(u,v):={(x,y)∈K×K:‖F1(x)+f1(x,y)‖+‖F2(y)+f2(x,y)‖≤‖F1(x)+f1(u,v)‖+‖F2(y)+f2(u,v)‖}。
步骤1 对任意的(u,v)∈K×K,(u,v)∈G(u,v),故G(u,v)≠∅。
步骤2 任意固定的(u,v)∈K×K,任意序列{(xn,yn)}⊂G(u,v),(xn,yn)→(x,y),有
‖F1(xn)+f1(xn,yn)‖+‖F2(yn)+f2(xn,yn)‖≤‖F1(xn)+f1(u,v)‖+‖F2(yn)+f2(u,v)‖。
因为Fi是连续、紧值映射,i=1,2,由引理1.1知Fi在Hausdorff度量下连续,由文献[15]知
|‖F1(xn)+f1(xn,yn)‖-‖F1(x)+f1(x,y)‖|≤H(F1(xn)+f1(xn,yn),F1(x)+f1(x,y))=0。
则有‖F1(xn)+f1(xn,yn)‖=‖F1(x)+f1(x,y)‖。
同理可得
‖F2(yn)+f2(yn,xn)‖=‖F2(y)+f2(y,x)‖,
‖F1(xn)+f1(u,v)‖=‖F1(x)+f1(u,v)‖,
‖F2(yn)+f2(v,u)‖=‖F2(y)+f2(v,u)‖。
故有
‖F1(x)+f1(x,y)‖+‖F2(y)+f2(x,y)‖≤‖F1(x)+f1(u,v)‖+‖F2(y)+f2(u,v)‖。
且(x,y)∈K×K,因此(x,y)∈G(u,v),故G(u,v)为闭集。
步骤3 由于K为X中的紧集,且对任意的(u,v)∈K×K,闭集G(u,v)⊂K×K,故对任意的(u,v)∈K×K,G(u,v)为紧集。

‖F1(u0)+f1(u0,v0)‖+‖F2(v0)+f2(v0,u0)‖>‖F1(u0)+f1(ui,vi)‖+‖F2(v0)+f2(ui,vi)‖。
因此当i=1,2,…,n时,有
‖F1(u0)+f1(u0,v0)‖+‖F2(v0)+f2(v0,u0)‖>max{‖F1(u0)+f1(ui,vi)‖+‖F2(v0)+f2(ui,vi)‖}。
‖F1(u0)+f1(u0,v0)‖≤max{‖F1(u0)+f1(ui,vi)‖,i=1,2,…,n},
‖F2(v0)+f2(v0,u0)‖≤max{‖F2(v0)+f2(ui,vi)‖,i=1,2,…,n}。
故‖F1(u0)+f1(u0,v0)‖+‖F2(v0)+f2(v0,u0)‖≤max{‖F1(u0)+f1(ui,vi)‖+‖F2(v0)+f2(vi,ui)‖},这与假设产生矛盾,因此假设不成立,故G是KKM映射。


定理2.2 设X为赋范空间,K是X中的非空凸紧集,fi:K×K→2X是连续、线性映射,Fi:K→2X是连续、凸紧值映射,则存在(x0,y0)∈K×K,使得

证明:定义集值映射G:K×K→2K×K,任意(u,v)∈K×K,
G(u,v):={(x,y)∈K×K:‖F1(x)+f1(x,y)‖+‖F2(y)+f2(x,y)‖≤‖F1(x)+f1(u,v)‖+‖F2(y)+f2(u,v)‖}。
由定理2.1的证明步骤1至步骤3可知G为非空、闭值和紧值映射。
下面用反证法证明G是KKM映射。假设存在有限点集{(ui,vi)}∈K×K,i=1,2,3,…,n,

‖F1(u0)+f1(u0,v0)‖+‖F2(v0)+f2(u0,v0)‖>‖F1(u0)+f1(ui,vi)‖+‖F2(v0)+g2(ui,vi)‖,i=1,2,…,n。


因为fi是线性映射,且Fi为凸值映射,i=1,2,由定理1.1有
故

这与假设产生了矛盾,因此假设不成立,故有G是KKM映射。

定理2.3 假设定理2.1的条件成立,对任意的(x,y)∈K×K,
0∈F1(x)+f1(K,K),0∈F2(y)+f2(K,K)
成立,则存在(x0,y0)∈K×K,使得问题(1)的解存在,即存在(x0,y0)∈K×K,使得
证明:由定理2.1知,存在(x0,y0)∈K×K,使得



‖F1(x0)+f1(x0,y0)‖+‖F2(y0)+f2(x0,y0)‖=0,

即存在(x0,y0)∈K×K,使得问题(1)的解存在。
类似地,由定理2.3推知有下述定理成立。
定理2.4 假设定理2.2的条件成立,对任意的(x,y)∈K×K,
0∈F1(x)+f1(K,K),0∈F2(y)+f2(K,K)成立,则存在(x0,y0)∈K×K,使得问题(1)的解存在,即存在(x0,y0)∈K×K,使得
3 耦合变分包含问题的相关问题
在这一部分,主要研究问题(1)的相关问题。应用定理2.3得到多值耦合重合点定理。
定理3.1 设X为赋范空间,K是X中的非空凸紧集,f:K×K→X为连续、几乎拟凸映射,F:K→2X是连续、紧值映射,i=1,2,使得f(K,K)⊆F(K),则f和F有一个多值耦合重合点。
证明:对任意的x,y∈K,令f1(x,y)=-f(x,y),f2(y,x)=-f(y,x),F1(x)=F(x),F2(y)=F(y),那么f和F满足定理2.3的要求,因此存在(x0,y0)∈K×K,使得
0∈F(x0)-f(x0,y0),0∈F(y0)-f(y0,x0),那么f(x0,y0)∈F(x0),f(y0,x0)∈F(y0),即f和F有一个多值耦合重合点。
推论3.1设X为赋范空间,K是X中的非空凸紧集,f:K×K→X为连续、几乎拟凸映射,g:K→X是连续映射,使得f(K,K)⊆g(K),则f和g有一个耦合重合点。
证明:对任意的x∈K,F(x)={g(x)},运用定理3.1,就可以得到f(x0,y0)=g(x0),f(y0,x0)=g(y0),即f和g有一个耦合重合点。
推论3.2设X为赋范空间,K是X中的非空凸紧集,f:K×K→X为连续,则f有一个耦合不动点。
证明:对任意的x∈K,g(x)=x,运用推论3.1,就可以得到f(x0,y0)=x0,f(y0,x0)=y0,即f有一个耦合不动点。
接下来,应用定理2.1得到耦合最佳逼近定理。
定理3.2 设X为赋范空间,K是X中的非空凸紧集,f:K×K→X为连续、几乎拟凸映射,F:K→2X是连续、紧值映射,i=1,2,则存在(x0,y0)∈K×K,使得

证明:对任意x,y∈K×K,令f1(x,y)=-f(x,y),f2(y,x)=-f(y,x),F1(x)=x,F2(y)=y,那么f,F满足定理2.1的要求,因此存在(x0,y0)∈K×K,使得结论成立。
推论3.3设X为赋范空间,K是X中的非空凸紧集,f:K×K→X为连续、几乎拟凸映射,g:K→X是连续映射,则存在(x0,y0)∈K×K,使得
证明:对任意的x∈K,令F(x)={g(x)},应用推论3.2,则存在(x0,y0)∈K×K,使得结论成立。
推论3.4设X为赋范空间,K是X中的非空凸紧集,f:K×K→X为连续映射,则存在(x0,y0)∈K×K,使得
证明:对任意的x∈K,令g(x)=x,应用推论3.3,则存在(x0,y0)∈K×K,使得结论成立。
