图形变换:解决几何问题的“杀手锏”
2022-06-21帅建卓
文/帅建卓

“图形变换”包括平移、翻折、旋转等,一般不改变图形的形状与大小,只改变图形的位置。你尝试过运用“图形变换”解题吗?告诉你,运用“图形变换”,可以让你在探究图形问题的过程中收获意外的惊喜。
一、“平移”——等量变换的捷径
例1如图1,在平面直角坐标系中,直线与y轴相交于点A,与反比例函数在第一象限内的图像相交于点B(n,1)。点C为直线AB上方反比例函数图像第一象限内一点,且△ABC的面积为9,求点C的坐标。
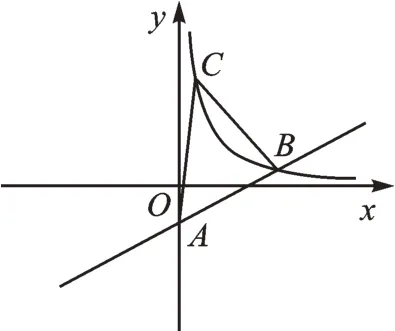
图1
【思路分析】利用点B确定反比例函数表达式后需要进一步思考△ABC的面积与点C坐标之间的关系。由于△ABC没有边与坐标轴平行或重合,直接求三角形的面积比较困难。那么,能否考虑将其转化为有一边与坐标轴平行或重合的三角形呢?答案是肯定的。将直线AB向上平移且经过点C,交y轴于点D(如图2),由平行线间距离处处相等得S△ABC=S△ABD=9,从而求得则直线CD表达式为再将直线CD与反比例函数联立方程组即可求点C坐标为(1,4)。

图2
【反思归纳】我们在处理坐标与图形面积问题时,利用“平移”可达到“化斜为正”的目的,将不方便求解的三角形转化为底和高易求的图形。
二、“翻折”——线段重组的蹊径
例2如图3,在矩形ABCD中,AB=6,AD=3,动点P满足,则点P到A、B两点距离之和PA+PB的最小值是多少?
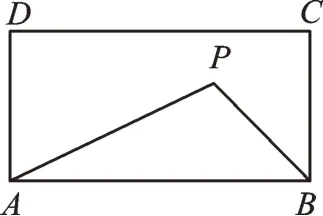
图3
【思路分析】本题从哪里入手呢?研读条件,我们可以发现:动点P相对于其他定点显得尤为突出,不妨从点P入手。那么点P如何运动呢?由于故△PAB中AB边上的高h=2,可见点P在距离AB上方2 个单位的直线l上运动(如图4)。一般来说,探究两条线段和最小的问题常常转化为两点之间的线段,利用两点之间线段最短来解决。要想知道点P在何处时PA+PB最小,而PA与PB又位于直线同侧,故可考虑将PA与PB两条线转化到直线两侧。转化的手段是“翻折”,将PA沿直线l翻折到PE的位置,由轴对称性质可知PA=PE,再由两点之间线段最短可知PE+PB≥BE,根据勾股定理得,即PA+PB的 最 小值为

图4
【反思归纳】“白日登山望烽火,黄昏饮马傍交河。”结合图4,我们可以将《古从军行》中的内容抽象为,将军观望烽火后从山脚A出发,再走到河边点P处饮马,最后回到B点宿营,求马的最短行程。本例也是运用“翻折”将著名的“将军饮马”问题进行转化的经典案例。
三、“旋转”——更换位置的妙法
例3如图5,△ABC是边长为7 的等边三角形,P为平面内一点,且PA=8,求PB+PC的最小值。
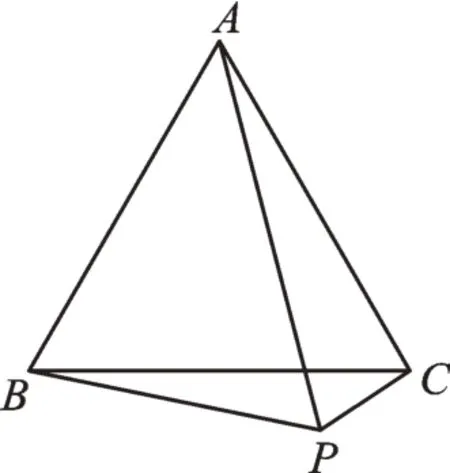
图5
【思路分析】根据例2 的分析,同学们可能会由例2 的经验考虑利用“翻折”转化。这里,点A可看成定点,而PA=8,故点P可看成在以A为圆心、8为半径的圆上运动,看来“翻折”方法行不通了。可不可以转化呢?我们尝试“旋转”。如图6,将△PBC绕点C顺时针“旋转”60°,使得点B与点A重合,点P落在P′处,则△PBC≌△P′AC,PB=P′A,CP=CP′。因为恰好旋转了60°,所以此时△PP′C为等边三角形,则PC=PP′,PB+PC=P′A+PP′。在△APP′中,P′A+PP′≥PA,当A、P′、P三点共线时,P′A+PP′最小为8,即PB+PC的最小值为8。
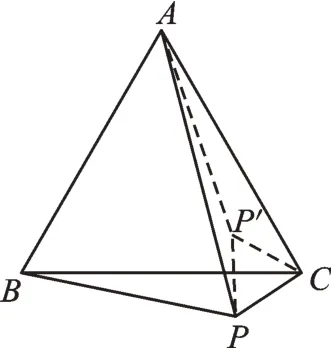
图6
【反思归纳】解决线段和(差)最大(小)问题时,如果用“翻折”受阻,而有等长线段(如等腰三角形、正方形)的条件时,不妨考虑“旋转”。
通过上面几道例题的分析,同学们是不是发现:“图形变换”能让你在探究图形问题的过程中收获意外的惊喜。因此,大家在探究图形问题时,要充分发挥想象力与创造力,多维度思考,多角度变换,合理构造,一定会有更大的收获。
