指数函数多项式的实根分离算法

2022-06-21葛昕钰陈世平刘忠

计算机应用 2022年5期

葛昕钰，陈世平，刘忠

（1.中国科学院成都计算机应用研究所，成都 610041； 2.中国科学院大学，北京 100049；3.四川省贸易学校财经商贸系，四川雅安 625107；4.乐山职业技术学院电子信息工程系，四川乐山 614000）（∗通信作者电子邮箱geeexy@163.com）

指数函数多项式的实根分离算法

葛昕钰1，2*，陈世平3，刘忠1，4

针对超越函数多项式的实根分离问题，提出了一种指数函数多项式的区间分离算法exRoot，将非多项式型实函数的实根分离问题转化为多项式正负性判定问题进而对其求解。首先，利用泰勒替换法构造目标函数的多项式区间套；然后，将指数函数的求根问题转化为多项式在区间内正负性的判定问题；最后，给出综合算法，并且试探性地应用于实特征值线性系统的可达性判定问题。所提算法在Maple中实现，输出的结果可读，且高效易行。区别于HSOLVER和数值计算方法fsolve，exRoot回避了直接讨论根的存在性问题，理论上具有终止性和完备性，且可达到任意精度，应用于最优化问题时可避免数值解带来的系统误差。

指数函数多项式；实根分离；泰勒替换法；区间列；终止性

0 引言

实根分离算法作为实代数的基本算法之一，不仅具有很强的理论意义，还有着广泛的应用前景。除了GCD（Greatest Common Divisor）算法、Sylvester结式、Descartes符号法则等经典工具外，对于多项式型函数实根分离的研究也有进展，例如Becker等［1］提出的Cisolate算法和Mehlhorn等［2］提出的渐进方法。而上述多项式型函数的实根分离算法对非多项式型实函数的实根求解问题并不适用，因此仍需进一步的研究［3-11］。目前求非多项式型实函数近似根的主要方法为迭代法，其过程中可能出现过分依赖初始近似值、迭代后局部收敛的问题，存在多个根时可能出现不收敛的情况。

在众多非多项式型实函数中，指数函数在机器人逆运动学、分片代数簇、化学反应器稳定性分析等工程问题中有许多应用，例如在实特征值线性系统的可达性判定中，多项式等式型约束即可转化为指数函数的实根分离。然而，用迭代法解决指数函数实根分离问题的过程同样会存在上述问题，并且没有消除超越因子，因此不能真正解决指数函数中的超越问题。由此，指数函数实根分离的自动证明和程序开发也成为人工智能和自动推理中重要且具有挑战的任务。

近年来也有学者对其自动证明算法进行研究：文献［11］中提出了针对exp-log-arctan型函数的实根分离方法，根据半傅里叶序列（semi-Fourier sequence）符号的变化数判定根的存在性，但算法的完备性依赖于尚未证明的Schanuel猜想；文献［12］中利用罗尔中值定理对多项式的伪倒数进行判定从而分离其实根，其方法直接应用于超越函数exp（x）、ln（x）、arctan（x）以解决实数范围的超越函数实根分离问题，部分决策过程已在计算机逻辑系统Redlog中实现；文献［13］中采用连分数构造指数函数多项式的区间套，从而估计指数函数多项式在有理点上的值。

为了更好地解决指数函数的实根分离问题，可将其理解为指数多项式在特定区间上的正负性判定问题。文献［3，14-17］中利用反正切函数泰勒展开式交错级数的特性设计了混合三角多项式不等式的泰勒替换法，其核心思想是先确定根所在的区间，再构造其上、下界多项式找到包含非多项式型实函数的有理函数多项式列，从而判定该区间上三角函数多项式正负性，进而实根分离。文献［3］中根据该算法已经完成了对三角函数多项式实根分离的自动求解程序，并在符号计算软件Maple中实现。延续在三角函数上的思想，文献［17］中提出了指数多项式不等式的判定方法。本文即在文献［17］研究的基础上，以指数多项式不等式的判定为主要工具，提出了针对形如f（x，）的指数函数的实根分离算法exRoot，并对指数函数的最优化问题进行了讨论，得到了极值所在的确定区间。

区别于文献［11-12］的方法，本文将非多项式型实函数的实根分离问题转化为多项式判定问题进而求解，回避了直接讨论根的存在性问题，并应用于多项式优化问题中。算法exRoot已经在Maple中实现程序，可自动输出含单根的区间列，且区间长度可以满足任意精度，形成完备且可读的证明过程。程序在Intel Core i5-6500 Windows x64 Maple2015环境下对随机生成的实例运行时长均未超过15 s。

1 指数多项式

先给出一些有关代数数和超越数的基本知识。

定义1［15］给定一个数a，若存在系数不全为零的整系数多项式P（x）使得P（a）=0，则称a是代数的或a是代数数，否则称a是超越数。

引理1［15］每一个代数数系数多项式的根也是代数数。

定义2［15］给定二元有理系数多项式环Q［x，y］，将其中的变量y用eqx替换（），定义该环上的一个映射hom：f（x，y）→f（x，eqx）。二元有理多项式f（x，y）在该映射下的像F（x）=hom（f（x，y））=f（x，eqx）被称为指数多项式。记映射后的环为Q［x，eqx］。

定义3［17］x0称为实函数的重根，如果φ（x0）=φapos;（x0）=0。

引理2［17］若f（x，y）是二元有理多项式，那么指数多项式f（x，y）=f（x，ex）唯一可能的重根是0。

引理3若f（x，y）≢0，则F（x）=hom（f（x，y））≢0（此处f（x，y）≢0表示f（x，y）不恒等于0，下同）。

下面讨论mgt;0且cm（x）≢0的情况。假设f（x，y）≢0而F（x）=hom（f（x，y））≡0。由于（e2）n是超越的，而对有理多项式ci（2）是代数数。由定义2，F（e2）=cm（2）（e2）m+（++c0（2） =0说明cm（2）===c0（2）=0，代入则有f（x，y）≢0，与假设矛盾。综上所述，引理3成立。

定义在［0，+∞）的指数多项式具有环的代数结构，即hom是二元有理系数多项式环到指数多项式环的一个映射。由引理2可知映射hom是一对一的，显然也是Q［x，y］到Q［x，eqx］满射，那么存在其逆映射：F（x）=f（x，eqx）→f（x，y）。

引理4F（x）=f（x，ex）在求导运算下封闭。

引理5［17］对给定的二元有理多项式f（x，y），存在，使得指数多项式的任意正根。若变元序设定为，将f（x，y）按字典序降序排列，当xgt;MR时，若其首系为正，；若其首系为负，。

根据文献［17］中对引理5的证明过程，有算法1计算根的上界。

算法1 upBound。

输入二元有理多项式f（x，y）；

输出有理多项式f（x，y）根的一个上界MR。

BEGIN

END

其中realroot（f（x），r）是Maple中关于有理多项式的实根分离命令：输入有理多项式f（x）和精度r，返回一个互不相交的区间列。整个列表包含的实根，每个区间只包含一个实根，且各区间长度均不超过r。

引理6［16］对二元有理多项式f（x，y），F（x）=f（x，ex）在（0，+∞）内至多有有限个不同实根（重根只记一次）。

记G（x）在0点Taylor展开式的前n项之和为，例如，。可见，展开各项依次交错，对此构造其多项式列，进而实现指数函数的多项式型放缩。

定义4记，，记，对hom：y=ex有。当时，记，否则。记Fd（x）=hom（fd（x，y））。

显然f（x，y）=fd（x，y）·yn，那么对，有。

以下若未作特殊说明，均假设x∈（0，+∞）（对的讨论可作变量替换）。

定义5若在区间（0，T］（）内满足1）～3），则常数称为T的临界值，称在区间上可规范展开。

1）F（x）gt;0；

引理7［17］假设多项式T1（x）gt;0，T2（x）gt;0且，则。

引理8［17］当时，对任意有：

3）当n→∞ 时，。

定义6对任意，记为Fd（x）的一个上界多项式，记为Fd（x）的一个下界多项式。

引理9［17］对任意，当时，有：

1）Tmax（x，n，Fd（x））gt;F（x）gt;Tmin（x，n，Fd（x））；

3）当n→∞时，Tmax（x，n，Fd（x））→Fd（x），Tmin（x，n，。

对关于x的单变量多项式，有以下性质：

定理1［17］任意x∈（0，T］，Fd（x）=f（x，e-x）gt;0成立当且仅当。

定理2［17］任意x∈（0，T］，Fd（x）=f（x，e-x）lt;0成立当且仅当Tmax（x，n，Fd（x））≤0。

定理1和定理2说明函数在区间（0，T］上任意一有理点的正负性是可判定的。在此基础上本文设计了算法2，用来判定函数F（x）=f（x，ex）在区间（a，b）∈（0，T）上的值域与0的大小关系。具体思路如下：1）判定上界多项式是否在该范围内恒小于0，如果是，那么该段上函数值均为负，判定结果记为；2）判定下界多项式是否在该范围内恒大于0，如果是，那么该段上函数值均为正，判定结果记为1；3）判定在该范围内下界多项式小于0、上界多项式大于0，如果是，那么函数在该段正负性不确定，判定结果记为0；4）如果上述情况均不符合，则递归进行其项展开继续判定，直至得出判定结果。

由于区间端点均为有理数，因此端点值不会是非多项式型实函数的根，故在如下讨论中不考虑端点，均使用开区间。

算法2 determination。

输入 1）Fd（x）=f（x，），2）a（），3）b（）；

输出sgn。 #返回值sgn表示在区间（a，b）上的值域与0的关系：表示函数在该区间内值域下界大于0，表示函数在该区间内值域上界小于0；表示在该区间内值域包含0。

BEGIN

#该段函数值为正，算法结束

#该段正负性不定，算法结束

END

其中，prove（ineq，（a，b））表示对不等式ineq在区间（a，b）上的判定，ineq在（a，b）上成立则返回true，否则返回false。可通过Maple的不等式证明程序包Bottema中的判定工具xprove（ineq，［xgt;a，xlt;b］）实现。

定理3［17］对不可约二元有理多项式，算法2必然终止。

根据算法1和算法2有对应程序upBound（expr）、determination（expr，a，b）。

2 指数多项式的实根分离

2.1 指数多项式的实根分离算法

而判定fd（x，y）在区间（0，MR）内根的存在性的基本思路是：对不可约多项式fd（x，y），fd（x，y）在（a，b）上恒大于0或恒小于0，则在（a，b）上无实根；否则对fapos;d（x，y）进行判定，若在（a，b）上单调，则有唯一实根；若fd（x，y）在（a，b）上既不恒大于0，也不恒小于0，在（a，b）上也不单调，那么采用二分法分离区间，再递归进行判定。根据以上说明，本文构造了算法3用于实根分离。

算法3 isolation。

BEGIN

END

定理4若f（x，y）为不可约二元有理多项式，算法3必然终止。

证明f（x，y）在区间（0，T）上任意一有理点的正负性总是可判定的，并由引理6可知，f（x，y）最多有有限个根，那么判定过程必然是有限步的。过程采用二分法，保证各区间不相交。那么，算法3必然终止。

对已有但不满足精度要求的区间列，可用二分法分割区间直至满足精度要求（算法4）。

算法4 accuracy。

输入 1）Fd（x），2）Fd（x）的单根区间（a，b），3）给定精度r（rgt;0）；

输出（c，d）。#F（x）在（c，d）内有唯一根且

BEGIN

END

综上所述，本文提出综合算法5对多项式进行转化和判定：输入（此时）求出MR后，同除y的最高次幂将多项式变形为，运行算法3对其实根分离，得到区间列后采用算法4提升精度，输出满足设置精度的、互不相交的区间列，每个区间内有且只有一个根。

输入 1）二元有理多项式f（x，y），2）；

BEGIN

END

根据算法3、算法4和算法5有对应程序isolation（expr，a，b）、accuracy（expr，a，b，r）和exRoot（expr，r）。

例1，。

利用算法5求解该例过程如下：

c）输出区间列｛（0，1）｝。

4）运行accuracy（Fd（x），0，1，2，1/10），二分法求精度，结果为（11/16，3/4）。

2.2 实根分离算法应用实例

例2［13］指数函数多项式，考虑φ（x）的根。

对不可约多项式φ（x）有。

例4［18］对线性非齐次系统：

运行程序exRoot（f（x，y），1/4），得到结果为｛（3/4，1）｝。也就是说，该系统在内可达。

上述实例已在Intel Core i5-6500，Windows 7 x64， Maple2015环境下进行验证，运行时间如表1所示。其中，fsolve为Maple中实根隔离的数值工具，每次只能隔离出一个实根。同时，相较HSOLVER，exRoot对例4的计算时间明显较短，且例2的计算结果与fsolve一致。

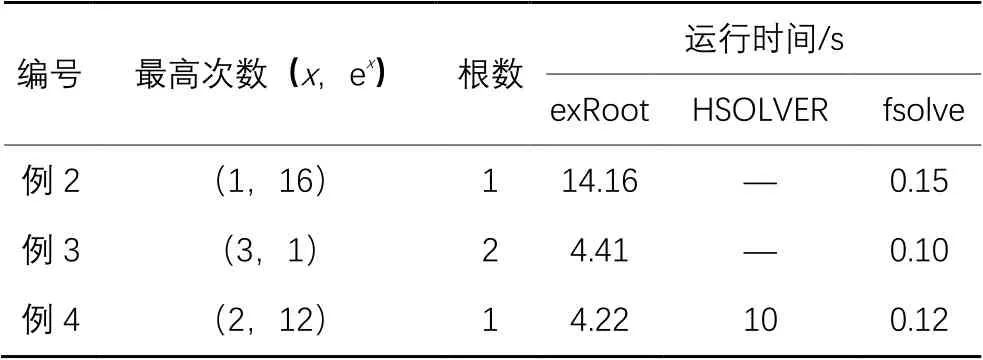
表1 实例运行时间Tab. 1 Running times of examples

3 最优化问题

3.1 最优化算法

同时，实根分离算法还可用于最优化问题。

定理5 对有理多项式F（x）有。

根据定理5可以由各极值比较得出最值点所在的区间。算法6（算法7）是比较两个极值区间中较大（小）的极值点所在的区间，这样可以通过算法8得到最值点所在的区间。

算法6 comparisonMax。

输入 1）F（x），2）极大值点（a1，b1），3）极大值点（a2，b2），4）n0；

BEGIN

END

算法7 comparisonMin。

输入 1）F（x），2）极小值点，3）极小值点，4）n0；

BEGIN

END

得到最值点区间后进而求出最值区间，同样利用定理5进行进一步放缩。

对最大值点所在区间（amax，bmax），有。

将F（x）的上、下界多项式代入，进一步得到。

对值域不满足精度要求的结果，可进一步通过算法4操作使其达到精度限制。

算法8 optimization。

输入 1）F（x），2）F（x）的驻点区间列，3）n0；

BEGIN

END

3.2 最优化算法应用实例

求解过程如下：

运行产生的分子分母大整数的分数会降低结果的可读性，可采取如下简化策略：将分数的分子分母从个位开始同时去掉若干位数（分母保留的位数不得低于，否则无法达到指定精度r），再将区间左端点的分母加1，右端点的分子加1，这样得到的区间是端点的分子分母的位数可以小于给定数且包含原区间的最小区间［3］。通过如上放缩后区间简化为，即F（x）最小值所在区间为。最优化过程在Intel Core i5-6500，Windows 7 x64操作系统，Maple2015环境下运行时间0.87 s。

4 结语

本文在指数函数多项式判定算法的基础上，将指数函数的实根分离问题转化为多项式判定问题进而求解，实现了指数函数实根分离的完全算法exRoot。该算法回避了根的存在性问题，找出了包含全部实根且区间互不相交的区间列（每个区间有且仅有一个实根），区间长度可达到任意精度。然后将其应用于多项式优化问题中，通过对指数多项式导数的实根分离得到驻点存在的区间，最终得到极值的确定范围。本文解决了一类超越函数解的问题，简单易行，十分高效。

[1] BECKER R， SAGRALOFF M， SHARMA V， et al. A near-optimal subdivision algorithm for complex root isolation based on the Pellet test and Newton iteration ［J］. Journal of Symbolic Computation， 2018， 86： 51-96.

[2] MEHLHORN K， SAGRALOFF M， WANG P M. From approximate factorization to root isolation with application to cylindrical algebraic decomposition ［J］. Journal of Symbolic Computation， 2015， 66：34-69.

[3] 陈世平，刘忠.三角函数多项式的实根分离［J］.汕头大学学报（自然科学版），2016，31（3）：25-39.（CHEN S P， LIU Z. Real root isolation of trigonometric function polynomial ［J］. Journal of Shantou University （Natural Science Edition）， 2016， 31（3）：25-39.）

[4] 杨路，夏壁灿.不等式机器证明与自动发现［M］.北京：科学出版社，2008：126-130.（YANG L， XIA B C. Inequality Machanical Proving and Automatic Discovery ［M］. Beijing： Science Press， 2008： 126-130.）

[5] ACHATZ M， McCALLUM S， WEISPFENNING V. Deciding polynomial-exponential problems ［C］// Proceedings of the 2008 21st International Symposium on Symbolic and Algebraic Computation. New York： ACM， 2008： 215-222.

[6] WU W T. Basic principles of mechanical theorem proving in elementary geometries ［J］. Journal of Automated Reasoning， 1986， 2（3）： 221-252.

[7] BUCHBERGER B， COLLINSS G E， KUTZLER B. Algebraic methods for geometric reasoning ［J］. Annual Review of Computer Science， 1988， 3： 85-119.

[8] YANG L， ZHANG J. A practical program of automated proving for a class of geometric inequalities ［C］// Proceedings of the 2000 International Workshop on Automated Deduction in Geometry， LNCS 2061. Berlin： Springer， 2000： 41-57.

[9] 陆征一，何碧，罗勇.多项式系统的实根分离算法及其应用［M］.北京：科学出版社，2004：34-44. （LU Z Y， HE B， LUO Y， Real Root Isolation Algorithm of Polynomial System and Its Applications ［M］. Beijing： Science Press， 2004： 34-44.）

[10] DAI L Y， FAN Z， XIA B C， et al. Logcf： an efficient tool for real root isolation ［J］. Journal of Systems Science and Complexity，2019， 32（6）： 1767-1782.

[11] STRZEBOŃSKI A. Real root isolation for exp-log-arctan functions ［J］. Journal of Symbolic Computation， 2012， 47（3）： 282-314.

[12] MCCALLUM S， WEISPFENNING V. Deciding polynomial-transcendental problems ［J］. Journal of Symbolic Computation， 2012， 47（1）： 16-31.

[13] 徐鸣.程序验证与系统分析中的若干符号问题［D］.上海：华东师范大学，2010：11-20.（XU M. Some symbolic computation issues in program verification and system analysis ［D］. Shanghai： East China Normal University， 2010： 11-20.）

[14] CHEN S P， LIU Z. Automated proof of mixed trigonometric-polynomial inequalities ［J］. Journal of Symbolic Computation， 2020， 101： 318-329.

[15] 陈世平，刘忠.一类超越函数多项式不等式的自动证明［J］.系统科学与数学，2019，39（5）：804-822.（CHEN S P， LIU Z. Automated proving for a class of transcendental-polynomial inequalities ［J］. Journal of Systems Science and Mathematical Sciences， 2019， 39（5）： 804-822.）

[16] 陈世平，刘忠.三角函数多项式不等式的自动证明［J］.汕头大学学报（自然科学版），2015，30（3）：43-55.（CHEN S P， LIU Z. Automated proving of trigonometric function polynomial inequalities ［J］. Journal of Shantou University （Natural Science Edition）， 2015， 30（3）： 43-55.）

[17] 陈世平，刘忠.指数多项式不等式的自动证明［J］.系统科学与数学，2017，37（7）：1692-1703.（CHEN S P， LIU Z. Automated proving of exponent polynomial inequalities ［J］. Journal of Systems Science and Mathematical Sciences， 2017， 37（7）： 1692-1703.）

[18] XU M， CHEN L Y， ZENG Z B， et al. Reachability analysis of rational eigenvalue linear systems ［J］. International Journal of Systems Science，2010， 41（12）： 1411-1419.

Real root isolation algorithm for exponential function polynomials

GE Xinyu1，2*， CHEN Shiping3， LIU Zhong1，4

（1.Chengdu Institute of Computer Application，Chinese Academy of Sciences，Chengdu Sichuan610041，China；2.University of Chinese Academy of Sciences，Beijing100049，China；3.Department of Finance and Commerce，Sichuan Trade School，Ya’an Sichuan625107，China；4.Department of Electronic Information Engineer ing，Leshan Vocational and Technical College，Leshan Sichuan614000，China）

For addressing real root isolation problem of transcendental function polynomials， an interval isolation algorithm for exponential function polynomials named exRoot was proposed. In the algorithm， the real root isolation problem of non-polynomial real functions was transformed into sign determination problem of polynomial， then was solved. Firstly， the Taylor substitution method was used to construct the polynomial nested interval of the objective function. Then， the problem of finding the root of the exponential function was transformed into the problem of determining the positivity and negativity of the polynomial in the intervals. Finally， a comprehensive algorithm was given and applied to determine the reachability of rational eigenvalue linear system tentatively. The proposed algorithm was implemented in Maple efficiently and easily with readable output results. Different from HSOLVERand numerical calculation method fsolve，exRoot avoids discussing the existence of roots directly， and theoretically has termination and completeness. It can reach any precision and can avoid the systematic error brought by numerical solution when being applied into the optimization problem.

exponential function polynomial; real root isolation; Taylor substitution method; sequence of intervals; termination

TP181

1001-9081（2022）05-1524-07

10.11772/j.issn.1001-9081.2021030440

2021⁃03⁃22；

2021⁃07⁃14；

2021⁃07⁃14。

四川省科学技术厅科技计划项目（2016GFW0048）。

葛昕钰（1995—），女，河南安阳人，博士研究生，CCF会员，主要研究方向：自动推理、机器证明；陈世平（1970—），男，四川遂宁人，高级讲师，博士，主要研究方向：机器证明、符号计算；刘忠（1968—），男，四川乐山人，教授，博士，主要研究方向：自动推理、机器证明。

This work is partially supported by Scientific and Technological Program of Science and Technology Department of Sichuan Province （2016GFW0048）.

GE Xinyu， born in 1995， Ph. D. candidate. Her research interests include automated reasoning， mechanical proving.

CHEN Shiping， born in 1970， Ph. D.， senior lecturer. His research interests include mechanical proving，symbolic computation.