基于非负矩阵分解与稀疏表示的多标签分类算法

包永春，张建臣，杜守信，张军军

（1.西安工程大学 计算机科学学院，西安 710048； 2.德州学院 计算机与信息学院，山东 德州 253023）（∗通信作者电子邮箱 baoyongchun2014@163.com）

基于非负矩阵分解与稀疏表示的多标签分类算法

包永春1*，张建臣2，杜守信1，张军军1

（1.西安工程大学 计算机科学学院，西安 710048； 2.德州学院 计算机与信息学院，山东 德州 253023）（∗通信作者电子邮箱 baoyongchun2014@163.com）

传统的多标签分类算法是以二值标签预测为基础的，而二值标签由于仅能指示数据是否具有相关类别，所含语义信息较少，无法充分表示标签语义信息。为充分挖掘标签空间的语义信息，提出了一种基于非负矩阵分解和稀疏表示的多标签分类算法（MLNS）。该算法结合非负矩阵分解与稀疏表示技术，将数据的二值标签转化为实值标签，从而丰富标签语义信息并提升分类效果。首先，对标签空间进行非负矩阵分解以获得标签潜在语义空间，并将标签潜在语义空间与原始特征空间结合以形成新的特征空间；然后，对此特征空间进行稀疏编码来获得样本间的全局相似关系；最后，利用该相似关系重构二值标签向量，从而实现二值标签与实值标签的转化。在5个标准多标签数据集和5个评价指标上将所提算法与MLBGM、ML2、LIFT和MLRWKNN等算法进行对比。实验结果表明，所提MLNS在多标签分类中优于对比的多标签分类算法，在50%的案例中排名第一，在76%的案例中排名前二，在全部的案例中排名前三。

多标签分类；非负矩阵分解；稀疏表示；多输出回归；机器学习

0 引言

分类问题是机器学习中一类十分重要的问题。传统的分类问题一般为二分类或多类分类问题。二分类是指一个对象属于两个类别中的一个，例如垃圾邮件分类；多类分类是指一个对象属于多个类别中的一个，例如手写体数字识别。这些传统的分类方法考虑的对象都只有一个标签，具有单一语义，通常把这种传统的分类方法称作单标签分类方法。不同于传统的单标签分类方法，多标签分类［1］的对象通常同时和多个标签相关联，同时属于多个类别。这种对象在实际中也更为常见，在现实生活中，各种不同事物往往同时具有多种语义或可被同时归为多种类别或同时具有多种类别标签，例如：一部电影，可同时被标注为剧情、喜剧、奇幻等多个标签；一篇新闻报道，可同时被归为经济、政治、文化等类别。随着多标签分类技术的发展，多标签学习受到学界和业界的广泛关注，已被成功应用于多标签文本分类［2-3］、生物信息学［4-5］、图像标注［6-8］、视频标注［9］等不同领域。

随着多标签分类技术的发展，大量多标签分类算法不断涌现。目前已出现的多标签分类算法大致可分为问题转换型和算法适应型两种类型［10］。对于问题转换型算法，其策略是将多标签分类问题转换成一个或多个单标签分类问题，从而可以更加方便地应用现有传统分类方法来解决问题，如二元关联（Binary Relevance， BR）算法［11］、分类器链（Classifier Chains， CC）算法［12］、成对比较排序（Ranking by Pairwise Comparison， RPC）算法［13］、标准标签排序（Calibrated Label Ranking， CLR）算法［14］等。对于算法适应型方法，其策略是通过扩展传统单标签分类算法来直接处理多标签数据，如基于支持向量机的方法Rank-SVM（Ranking Support Vector Machine）［15］、基于实例（instance）的方法MLKNN（Multi-LabelK-Nearest Neighbor）［16］、基于神经网络的方法BP-MLL（Multi-Label Learning with BP neural network）［17］等。

然而，以上这些多标签分类算法存在一些类似的问题，即这些算法都是以原始二值标注的标签向量作为基础，这种二值标注的标签向量仅能指示数据是否具有相关类别，所含语义信息较少，且不能精确反映数据中不同类别的相对重要程度。实际上，对于一个具有多个标签的对象，每个标签的相对重要程度是不同的。例如，在同一幅图像中不同标签之间的相对重要性是不同的（虽然没有直接标注出每个标签的重要性，但是一般可以通过对图像中对象位置（前景、背景）和所占图像面积等观察得到。一般来说，对象在图像中位置越靠前，所占面积越大，对应标签就越重要），或者不同图像中同一标签的所占重要性也是不相同的。如果能将样本对象的二值标签通过某种方式改造为实值标签，将能丰富标签的语义信息，也能帮助更好地完成多标签分类任务。

在多标签分类中，样本的标签之间存在相关性。例如，如果一部电影被标志为“哈利波特”，那它很可能也会被标记为“魔法”“英国”；如果一幅图像被标志为“热带”“森林”，那么它几乎不可能同时被标注为“南极”。这种相关性为多标签分类任务带来了方便，如果能合理利用标签之间的相关性关系，将对多标签学习有很大帮助。同时，多标签数据集中标签规模通常很大，人类在进行繁重的标注工作时，难免会出现一些不正确的标注。这些噪声标签信息的存在，使得估计类标签之间的相关性变得困难，进而对学习性能产生负面影响。此外，“维数灾难（curse of dimensionality）”问题同样存在于高维的标签空间中，为了能有效处理高维标签数据，在多标签学习过程中通常会对其进行降维。

基于以上分析，针对原始二值标签所含语义信息较少的问题，为了充分挖掘标签空间语义信息，本文提出了一种基于非负矩阵分解和稀疏表示的多标签分类算法（Multi-Label classification algorithm based on Non-negative matrix factorization and Sparse representation， MLNS）。该算法结合了非负矩阵分解（Non-negative Matrix Factorization， NMF）技术和稀疏表示技术，可以将二值标签向量转换为实值标签向量，丰富标签语义信息，提高分类效果。具体来说，首先通过非负矩阵分解，将原始的多标签信息映射到一个低维的潜在语义空间中，该潜在语义空间不仅保留了标签之间的相关性，而且极大减少了原始标签空间中的噪声信息。然后，将分解后得到的低维标签向量与原始样本特征向量结合，形成新的特征空间，在该特征空间中，通过稀疏表示技术挖掘样本间的结构信息，并利用这些样本间结构信息，将原来的二值标签向量变换为实值标签向量。最终，将多标签分类问题转化为多输出回归问题。本文所提算法的主要工作如下：

1）利用稀疏表示技术，挖掘样本间结构信息，并依据此结构信息，将二值标签向量转化为实值标签向量，丰富标签语义信息。

2）利用对标签空间进行非负矩阵分解，获取标签之间的高阶相关性，同时减少标签噪声信息，降低标签空间维度。

3）将分解后得到的低维标签矩阵和原始特征矩阵结合，减少后续对样本间结构关系挖掘时的信息丢失。

1 相关工作

1.1 多标签学习

在多标签分类中，每个对象样本（example）的样本数据均由两部分组成，即描述对象属性的示例（instance）（由特征向量表示）和描述对象类别标签的标签（label）（由标签向量表示）。由多个描述对象的样本数据构成训练集（training set），在此训练集上，多标签分类的任务就是通过算法在训练集上的训练，得到一个分类模型，对于一个未知示例（unseen instance），该模型能够根据未知示例的特征向量来预测该未知示例所拥有的标签集合。形式化地讲，用代表原始维特征空间，表示用来描述样本的属性个数为；用代表与原始维特征空间相对应的维标签空间，表示每个样本可拥有个标签。假设代表由多个对象样本构成的训练集，其中样本个数为，代表多标签样本的特征向量，代表与当前样本相对应的标签向量。对于一个样本，如果该样本拥有第个标签，则标签向量对应第个位置为1，否则为0。多标签分类算法学习的目标是：通过对样本的特征空间（输入空间）进行挖掘，进而学得从特征空间到标签空间（输出空间）的映射，即，该映射关系即为分类器，通过应用学得的映射关系，就能对未见示例进行预测，判断其所属的标签集合。

在多标签分类中，随着标签数量的增加，其标签输出空间大小呈指数级增长，即对拥有个类别标签的样本集来说，其输出空间中标签子集规模为。为了应对输出空间如此巨大这种情况，提高多标签分类模型的健壮性和泛化性能，通常会利用标签之间的相关性。依照对标签之间相关关系利用程度的不同，可以把多标签分类算法分为三类：

1）一阶算法（First-order algorithm）。这类算法没有利用标签之间的相关性，通常是把原始的多标签分类问题转换为利用传统分类算法进行求解。此类算法通常为每个类别标签设计一个分类函数，如果训练样本拥有标签，那么在学习与标签对应的分类器时，该训练样本可以视为关于标签的正样本，反之被视为负样本。这类算法的优点是设计简单、思路清晰，方便理解，计算复杂度低；但由于此类算法在解决多标签分类任务的过程中，没有利用标签之间的相关性关系，不利于分类精度的进一步提高。BR算法和ML-KNN算法是一阶算法的代表。

2）二阶算法（Second-order algorithm）。这类算法利用两两标签之间的成对关系，通常就是利用样本中相关标签和无关标签之间的排序关系［18-23］。具体来说，如果训练集中某样本拥有标签，但不拥有标签，那么算法模型对于该样本关于标签产生的预测置信度值应大于关于标签产生的预测置信度值。相较于一阶算法，二阶算法总体上会有更为优异的表现；但是，通常仅考虑两两标签之间的关系，在实际应用中有一定的局限性，因此考虑标签之间更高阶关系的算法也大量出现。BP-MLL算法是二阶算法的代表。

3）高阶算法（High-order algorithm）。此类算法考虑更为高阶的标签之间的任意关系，即当前数据样本集中当前标签与其他剩余标签之间的相关关系或者此标签子集与其他任意标签子集之间的相关关系，这种对标签之间高阶关系进行建模的方式也更符合现实。但到目前为止，这类算法由于算法计算复杂度太高，存储成本大，不能较好地推广使用。CC算法及其扩展算法是典型的高阶算法。

1.2 非负矩阵分解

文献［24］中给出了非负矩阵分解定义，其核心思想是对于任意一个给定的非负矩阵，利用非负矩阵分解（NMF）算法能够将其分解为两个规模更小的非负矩阵的乘积，其数学表达式为：

NMF算法由于算法本身的特点，能够同时降低数据的维度和保留原始数据的主要特征，常被应用到数据挖掘和机器学习领域。

1.3 稀疏表示

稀疏表示理论最早被应用在信号处理领域［25］，主要是指信号中非零系数样本数量远小于信号长度，可以借助于少量的原子信号以线性的方式对原始信号进行近似表示。人类视觉系统的感知过程为稀疏表示提供了依据，人类视觉系统上的神经元只有极少数对于外界的不同刺激存在响应。这种特性成为视觉系统对自然图像高效编码的策略，自然图像能够被结构基元如边缘和结构等表示，得到的表示系数也是稀疏的［26］。

稀疏表示最初只是一种信号表示方式，用于解决信号处理领域的信号表示问题。随着稀疏表示在人脸识别［27］上的有效应用，其在机器学习领域的应用也变得更广泛。宋相法等［28］提出了基于稀疏表示的多标记学习算法，该算法利用训练集样本对测试数据进行稀疏重构。关于稀疏表示，可以形式化为：

2 本文算法

2.1 符号说明

2.2 标签空间分解

受文献［29］启发，本文提出了一种有效的将多标签输出空间分解为低维潜在语义空间的方法。该低维空间保留了原始标签空间中大部分结构信息，同时，又极大减少了空间中的噪声和冗余信息。形式化地讲，通过最小化以下重构误差，将多标签输出空间分解为两个低维非负矩阵和的乘积：

为了衡量原始待分解矩阵与分解后的两个非负矩阵乘积之间的误差，通常会定义损失函数，式（3）是基于欧氏距离的损失函数，最小化损失函数才能保证分解后的两个矩阵的乘积尽可能逼近原始的待分解矩阵。因此，可以将非负矩阵的目标函数优化问题描述为：

使用交替迭代法求解式（4）的乘性迭代规则可以描述为：

非负矩阵分解算法的具体步骤如算法1所示。

算法1 非负矩阵分解算法。

2.3 稀疏表示

2.4 二值标签映射为实值标签

2.5 多输出回归模型

通过上一步，将二值标签向量改造成实值标签之后，原来的多标签分类问题就变成了多输出回归问题，可以使用多输出支持向量回归（Multi-output Support Vector Regression， MSVR）［33］来建立模型。一般来说，MSVR要最小化下面的目标函数：

本文使用迭代加权最小二乘法（IteRative Weighted Least Square method，IRWLS）［34］对式（9）进行求解。具体的，使用的一阶泰勒展开来构造IRWLS过程，则经过轮迭代后有：

通过以上步骤，最终完成了本文的MLNS多标签分类模型。在测试阶段，即可通过该模型获得测试样本的预测输出，其中为实值向量，表示预测该测试样本具有每类标签的概率，而不再是简单地判断有或无此类标签的问题。本文采用阈值策略SCut设置阈值为，如果，则将标签设置为1，代表预测该测试样本存在标签；否则为0，代表预测该测试样本没有该标签，完成对测试样本的多标签分类。整体的MLNS如算法2所示。

算法2 MLNS算法。

下面对本文所提算法的复杂度进行分析。MLNS在运行过程中主要包括三个主要阶段：非负矩阵分解、稀疏重构和多输出回归。非负矩阵分解和稀疏重构的时间复杂度为；在多输出回归中如果选择多输出支持向量回归来实现分类，则时间复杂度为，因此总时间复杂度为。对于MLNS来说，在空间开销方面，由于算法运行过程中需要存储、、、、、、、等矩阵，这些矩阵需要占用的内存空间尺寸不超过、、、、、、、，因此总的算法空间复杂度为。由此可以看出，MLNS无论是时间复杂度（多项式的时间复杂度）还是空间复杂度都较小，在数据集样本数不是特别大的情况下，由2.6 GHz处理器和4 GB内存的单机即可完成实验。

3 实验和结果分析

3.1 数据集

本文实验共使用5个有代表性的数据集，涵盖了4个领域：音频、文本、图像和生物学。所有这些数据资源都可以从MULAN和WEKA中收集到。表1给出了数据集的具体指标：、和分别代表数据集的实例数、实例属性维数和数据集标签个数；为平均标签个数；为标签密度。

表1 数据集属性Tab. 1 Dataset properties

3.2 评价指标

本文中，在5个多标签评价指标上将MLNS和其他四个多标签学习方法进行实验比较。这些评价指标分为两个类别：基于样本的评价指标和基于标签的评价指标。基于样本的评价指标是首先获得算法在每个测试样本上的度量值，然后返回算法在整个测试集的平均值。与基于样本的评价指标不同，基于标签的评价指标首先获得算法在每个标签上的度量值，然后返回所有标签上的宏/微观平均F1值。

本文采用单误差one‑error、覆盖度coverage、排序损失ranking loss、平均精度average precise和宏平均值Mac‑F1进行算法性能评价，其中Mac‑F1是基于标签的度量，其余是基于样本的评价指标。设为多标签测试集，为标签属于对应实例的置信度。可以方便地转变为标签排名函数，即如果成立，则。5个评价指标的定义如下。

1）单误差one‑error：

2）覆盖度coverage：

3）排序损失ranking loss：

4）平均精度average precise：

3.3 对比算法

为了检验MLNS的有效性，本文选择了4种多标签分类算法MLBGM（Multi-Label classification Based on Gravitational Model）［35］、ML2（Multi-Label Manifold Learning）［36］、LIFT（multi-Label learning with label-specific FeaTures）［37］和MLRWKNN（Multi-Label classification based on the Random Walk graph and theK-Nearest Neighbor algorithm）［38］进行对比实验。MLBGM算法通过运用物理学经典的引力模型并建立标签的正、负相关性矩阵来挖掘标签间不同的相关关系。实验中，本文使用MLBGM算法参数的默认设置，即近邻数。ML2是第一个尝试在标签空间上探索流形的多标签分类算法。ML2的默认参数取值分别为：，，。LIFT通过聚类的方式重新构造标签相关特征集，以区分不同的标签，参数采用默认设置为。MLRWKNN算法通过对测试实例的k近邻样本构造随机游走图的顶点集和近邻样本标签间的相关边集探索标签之间的依赖关系。实验中对于所有参数均采用默认设置，即近邻数，转移概率，调整因子为最大样本间欧氏距离。对于本文所提算法MLNS，参数设置为，，。

3.4 结果分析

本文实验硬件环境为：Intel Core i5-2400 CPU 3.10 GHz 4核，8 GB内存。软件环境为：Windows 10旗舰版，Eclipse 4.8.0，Matlab 2016a，jdk1.8.0_25-x64，Weka3.7.10，Mulan1.4.0。对于实验中的每个数据集，本文采用10折交叉验证方式。表2给出了不同算法在不同多标签数据集上的性能表现，具体来说，表中记录了不同算法在不同数据集上相应评价指标的平均值和标准差。对于每个评价指标，“↓”表示值越小算法性能越好，“↑”表示值越大算法性能越好，最好的结果均做加粗处理。

表2 不同算法在多标签数据集上的性能（均值±标准差）Tab. 2 Performance of different algorithms on multi-label datasets （mean value±standard deviation）

本文使用基于算法排序的Friedman Test［39］来检验算法是否具有统计意义上的显著性差别。如果假设“所有算法的性能相同”被拒绝，则说明算法的性能显著不同。具体算法为：

从表3可以得到，“所有算法的性能相同”原假设在置信度水平为0.05的条件下被拒绝，因此进行后续检验Bonferroni-Dunn test［40］来进一步区分各算法。一般认为两个算法的平均排序值之差超过一个临界值域CD（Critical Difference）值时，则认为两个算法有显著性不同。临界值域CD可以表示如下：，其中，，显著性水平0.05下的。MLNS及其对比算法的CD图如图1所示，横轴数值代表每个算法在不同评价指标下的平均排名，以实线相连的各算法在性能上没有显著差异。

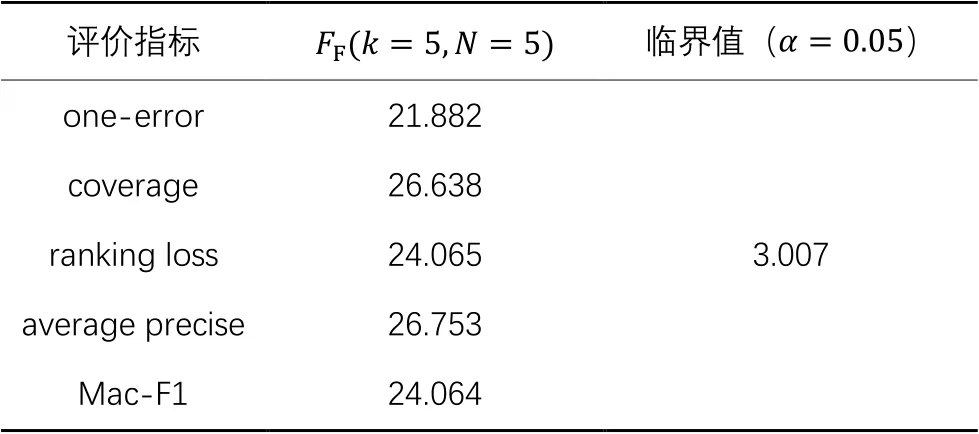
表3 Friedman检验和各项评价指标的临界值Tab. 3 Friedman test and critical value of each evaluation metric

通过上述实验结果的分析，可以得出以下结论：在one- error、coverage、ranking loss、average precise、Mac-F1这5个评价指标上，本文所提MLNS平均排名值都是最优的（平均排序越小，对应算法性能越好），表明MLNS性能优于其他对比算法。对于实验中的5个多标签数据集，在不同的5个评价指标下，MLNS在50%的案例中排名第一，在76%的案例中排名前二，在全部的案例中排名前三，表明本文所提算法在完成多标签分类任务上具有优于其他算法的性能，验证了本文所提算法通过将二值标签改造为实值标签再进行多标签分类的有效性。在image数据集上，MLNS在所有评价指标上的表现都是最好的，可以认为MLNS更“偏好”图像类数据集。

图1 利用Bonferroni-Dunn test比较所提MLNS与其他算法Fig. 1 Comparison of proposed MLNS and other algorithms by Bonferroni-Dunn test

4 结语

为实现二值标签到实值标签的改造，提升多标签分类的效果，本文提出了一种新的多标签分类算法MLNS。该算法首先采用非负矩阵分解的方式来获取标签的潜在语义信息，通过结合原始属性特征构造新的属性特征，减少了标签变换中的信息损失；其次，基于稀疏表示学得示例样本间的全局相似关系；然后，利用示例间关系，完成标签实值化改造；最后，将原始多标签分类问题转化为多输出回归问题。实验结果表明，本文所提MLNS的性能优于对比的其他多标签分类方法。接下来，我们将进一步考虑将非负矩阵分解和多标签分类技术相结合构造联合优化问题的模型，以考虑更复杂的标签相关性。

[1] GIBAJA E， VENTURA S. A tutorial on multilabel learning ［J］. ACM Computing Surveys， 2015， 47（3）： Article No.52.

[2] LI C S， WEI F， YAN J C， et al. A self-paced regularization framework for multilabel learning ［J］. IEEE Transactions on Neural Networks and Learning Systems， 2018， 29（6）： 2660-2666.

[3] BURKHARDT S， KRAMER S. Online multi-label dependency topic models for text classification ［J］. Machine Learning， 2018， 107（5）： 859-886.

[4] BARUTCUOGLU Z， SCHAPIRE R E， TROYANSKAYA O G. Hierarchical multi-label prediction of gene function ［J］. Bioinformatics， 2006， 22（7）： 830-836.

[5] WEINER M F， LIPTON A M. The Dementias： Diagnosis，Treatment， and Research ［M］. 3rd ed. Washington， DC： American Psychiatric Association Publishing， 2003： 1-25.

[6] FU H Z， CHENG J， XU Y W， et al. Joint optic disc and cup segmentation based on multi-label deep network and polar transformation ［J］. IEEE Transactions on Medical Imaging， 2018， 37（7）： 1597-1605.

[7] ZHUANG N， YAN Y， CHEN S， et al. Multi-label learning based deep transfer neural network for facial attribute classification ［J］. Pattern Recognition， 2018， 80： 225-240.

[8] WU B Y， JIA F， LIU W， et al. Multi-label learning with missing labels using mixed dependency graphs ［J］. International Journal of Computer Vision，2018， 126（8）： 875-896.

[9] LIU A A， SHAO Z， WONG Y， et al. LSTM-based multi-label video event detection ［J］. Multimedia Tools and Applications， 2019，78（1）： 677-695.

[10] ZHANG M L， ZHOU Z H. A review on multi-label learning algorithms ［J］. IEEE Transactions on Knowledge and Data Engineering， 2014， 26（8）： 1819-1837.

[11] BOUTELL M R， LUO J B， SHEN X P， et al. Learning multi-label scene classification ［J］. Pattern Recognition， 2004， 37（9）： 1757-1771.

[12] READ J， PFAHRINGER B， HOLMES G， et al. Classifier chains for multi-label classification ［J］. Machine Learning， 2011， 85（3）： 333-360.

[13] FÜRNKRANZ J， HÜLLEMEIER E. Pairwise preference learning and ranking ［C］// Proceedings of the 2003 European Conference on Machine Learning， LNCS 2837. Berlin： Springer， 2003： 145-156.

[14] FÜRNKRANZ J， HÜLLEMEIER E， LOZA MENCÍA E， et al. Multilabel classification via calibrated label ranking ［J］. Machine Learning， 2008， 73（2）： 133-153.

[15] ELISSEEFF A， WESTON J. A kernel method for multi-labelled classification ［C］// Proceedings of the 2001 14th International Conference on Neural Information Processing Systems. Cambridge： MIT Press， 2001： 681-687.

[16] ZHANG M L， ZHOU Z H. ML-KNN： a lazy learning approach to multi-label learning ［J］. Pattern Recognition， 2007， 40（7）： 2038-2048.

[17] ZHANG M L， ZHOU Z H. Multilabel neural networks with applications to functional genomics and text categorization ［J］. IEEE Transactions on Knowledge and Data Engineering， 2006， 18（10）： 1338-1351.

[18] UEDA N， SAITO K. Parametric mixture models for multi-labeled text ［C］// Proceedings of the 2002 15th International Conference on Neural Information Processing Systems. Cambridge： MIT Press， 2002： 737-744.

[19] ZHU S H， JI X， XU W， et al. Multi-labelled classification using maximum entropy method ［C］// Proceedings of the 2005 28th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval. New York： ACM， 2005： 274-281.

[20] LOZA MENCÍA E， FÜRNKRANZ J. Efficient pairwise multilabel classification for large-scale problems in the legal domain ［C］// Proceedings of the 2008 Joint European Conference on Machine Learning and Knowledge Discovery in Databases， LNCS 5212. Berlin： Springer， 2008：50-65.

[21] HÜLLERMEIER E， FÜRNKRANZ J， CHENG W W， et al. Label ranking by learning pairwise preferences ［J］. Artificial Intelligence， 2008，172（16/17）： 1897-1916.

[22] GHAMRAWI N， McCALLUM A. Collective multi-label classification ［C］// Proceedings of the 2005 14th ACM International Conference on Information and Knowledge Management. New York： ACM， 2005： 195-200.

[23] ZHANG M L， ZHANG K. Multi-label learning by exploiting label dependency ［C］// Proceedings of the 2010 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2010： 999-1008.

[24] LEE D D， SEUNG H S. Algorithms for non-negative matrix factorization ［C］// Proceedings of the 2000 13th International Conference on Neural Information Processing Systems. Cambridge： MIT Press， 2000： 535-541.

[25] NYQUIST H. Certain topics in telegraph transmission theory ［J］.Proceedings of the IEEE， 2002， 90（2）： 280-305.

[26] OLSHAUSEN B A， FIELD D J. Sparse coding with an overcomplete basis set： a strategy employed by V1？ ［J］. Vision Research， 1997， 37（23）： 3311-3325.

[27] WRIGHT J， YANG A Y， GANESH A， et al. Robust face recognition via sparse representation ［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2009， 31（2）： 210-227.

[28] 宋相法，焦李成.基于稀疏表示的多标记学习算法［J］.模式识别与人工智能，2012，25（1）：124-129.（SONG X F， JIAO L C. A multi-label learning algorithm based on sparse representation ［J］. Pattern Recognition and Artificial Intelligence， 2012， 25（1）： 124-129.）

[29] PAPADIMITRIOU C H，RAGHAVAN P， TAMAKI H， et al. Latent semantic indexing： a probabilistic analysis ［J］. Journal of Computer and System Sciences， 2000， 61（2）： 217-235.

[30] DING C， LI T， PENG W， et al. Orthogonal nonnegative matrix tri-factorizations for clustering ［C］// Proceedings of the 2006 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2006： 126-135.

[31] TIBSHIRANI R. Regression shrinkage and selection via the lasso：a retrospective ［J］. Journal of the Royal Statistical Society， Series B （Statistical Methodology）， 2011， 73（3）： 273-282.

[32] BOYD S， PARIKH N， CHU E， et al. Distributed optimization and statistical learning via the alternating direction method of multipliers ［J］. Foundations and Trends in Machine Learning， 2010， 3（1）： 1-122.

[33] CHUNG W， KIM J， LEE H， et al. General dimensional multiple-output support vector regressions and their multiple kernel learning ［J］. IEEE Transactions on Cybernetics， 2015， 45（11）： 2572-2584.

[34] TUIA D， VERRELST J， ALONSO L， et al. Multioutput support vector regression for remote sensing biophysical parameter estimation ［J］. IEEE Geoscience and Remote Sensing Letters， 2011， 8（4）： 804-808.

[35] 李兆玉，王纪超，雷曼，等.基于引力模型的多标签分类算法［J］.计算机应用，2018，38（10）：2807-2811， 2821.（LI Z Y， WANG J C， LEI M， et al. Multi-label classification algorithm based on gravitational model ［J］. Journal of Computer Application， 2018， 38（10）：2807-2811， 2821.）

[36] HOU P， GENG X， ZHANG M L. Multi-label manifold learning ［C］// Proceedings of the 2016 30th AAAI Conference on Artificial Intelligence. Palo Alto： AAAI Press， 2016： 1680-1686.

[37] ZHANG M L， WU L. LIFT： multi-label learning with label-specific features ［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2015，37（1）： 107-120.

[38] WANG Z W， WANG S K， WAN B T， et al. A novel multi-label classification algorithm based onK-nearest neighbor and random walk ［J］. International Journal of Distributed Sensor Networks， 2020， 16（3）： 1-17.

[39] DEMŠAR J. Statistical comparisons of classifiers over multiple data sets ［J］. Journal of Machine Learning Research， 2006， 7： 1-30.

[40] DUNN O J. Multiple comparisons among means ［J］. Journal of the American Statistical Association， 1961，56（293）： 52-64.

Multi-label classification algorithm based on non-negative matrix factorization and sparse representation

BAO Yongchun1*， ZHANG Jianchen2， DU Shouxin1， ZHANG Junjun1

（1.School of Computer Science，Xi’an Polytechnic University，Xi’an Shaanxi710048，China；2.School of Computer and Information，Dezhou University，Dezhou Shandong253023，China）

Traditional multi-label classification algorithms are based on binary label prediction. However， the binary labels can only indicate whether the data has relevant categories， so that they contain less semantic information and cannot fully represent the label semantic information. In order to fully mine the semantic information of label space，a new Multi-Label classification algorithm based on Non-negative matrix factorization and Sparse representation （MLNS） was proposed. In the proposed algorithm，the non-negative matrix factorization and sparse representation technologies were combined to transform the binary labels of data into the real labels， thereby enriching the label semantic information and improving the classification effect. Firstly， the label latent semantic space was obtained by the non-negative matrix factorization of label space， and the label latent semantic space was combined with the original feature space to form a new feature space. Then， the global similarity relation between samples was obtained by the sparse coding of the obtained feature space. Finally，the binary label vectors were reconstructed by using the obtained similarity relation to realize the transformation between binary labels and real labels. The proposed algorithm was compared with the algorithms such as Multi-Label classification Based on Gravitational Model （MLBGM）， Multi-Label Manifold Learning （ML2）， multi-Label learning with label-specific FeaTures （LIFT） and Multi-Label classification based on the Random Walk graph and theK-Nearest Neighbor algorithm （MLRWKNN） on 5 standard multi-label datasets and 5 evaluation metrics. Experimental results show that， the proposed MLNS is better than the compared multi-label classification algorithms in multi-label classification， the proposed MLNS ranks top1 in 50% cases，top 2 in 76% cases and top 3 in all cases.

multi-label classification; non-negative matrix factorization; sparse representation; multiple output regression; machine learning

TP181

A

1001-9081（2022）05-1375-08

10.11772/j.issn.1001-9081.2021050706

2021⁃05⁃06；

2021⁃09⁃07；

2021⁃09⁃16。

西安市科技计划项目（2020KJRC0027）。

包永春（1996—），男，山东菏泽人，硕士研究生，主要研究方向：机器学习、数据挖掘、人工智能； 张建臣（1974—），男，山东微山人，副教授，硕士，主要研究方向：人工智能、大数据分析； 杜守信（1995—），男，山东菏泽人，硕士，主要研究方向：智能制造； 张军军（1994—）男，陕西咸阳人，硕士，主要研究方向：人工智能、机器学习、深度学习。

This work is partially supported by Xi’an Science and Technology Program （2020KJRC0027）.

BAO Yongchun， born in 1996， M. S. candidate. His research interests include machine learning， data mining， artificial intelligence.

ZHAGN Jianchen， born in 1974， M. S.， associate professor. His research interests include artificial intelligence， big data analysis.

DU Shouxin， born in 1995， M. S. His research interests include intelligent manufacturing.

ZHANG Junjun， born in 1994， M. S. His research interests include artificial intelligence， machine learning， deep learning.