结合模型预测与目标规划的原材料订购策略

王慧，宋栋，郭渊博

摘  要： 研究如何在产量柔性条件下确定供货量和订购量，以助企业取得最佳的预期收益。首先运用SARIMA模型预测未来24周里每周供货商应满足的订货量，然后以保障生产稳定性和原材料订购结构优化为目标，建立目标规划模型;同时，考虑到实际供货量可能多于或少于订货量，引入风险因子反映供货量的波动特征;最后制定每周最经济的订购策略。实验结果表明，该模型具有良好的鲁棒性。

关键词： 订购决策; 目标规划; SARIMA模型; 风险因子

中图分类号：TP399          文献标识码：A     文章编号：1006-8228（2022）06-37-03

Raw material ordering policy combining model prediction and objective programming

Wang Hui1， Song Dong2， Guo Yuanbo1

（1. Cryptography Engineering Institute， Information Engineering University， Zhengzhou， Henan 450001， China;

2. Beijing Institute of Satellite Information Engineering）

Abstract： In this paper， we mainly focus on how to determine the quantity of supply and order under the condition of volume flexibility， so as to help the enterprise obtain the best expected profit. SARIMA model is used to predict the weekly order quantity that suppliers should meet in the next 24 weeks， and then an objective programming model is established to ensure production stability and optimization of raw material ordering structure. Considering that the actual supply may be more or less than the order， a risk factor is introduced to reflect the fluctuation characteristics of the supply. Finally， the most economical ordering strategy for each week is formulated. Experimental result shows that the model has good robustness.

Key words： ordering policy; objective programming; SARIMA model; risk factor

0 引言

當前，产品生命周期不断缩短，需求瞬息万变，竞争压力增加。如何在不确定性环境下制定订购策略，使得企业获取最佳收益，是本文研究的关键问题。Arnold[1]等人采用最优控制办法解决企业最优订购与库存战略问题;Zhang Minjie[2]通过构建基于选择性订购策略的订购模型，解决何时对原材料补充订购以及订购量是多少等问题;Meiyan Chen[3]提出了基于EOQ模型的确定性需求分析;Zhang Xiaoyue[4]等人提出了竞争订购策略;Yang Zhiyuan[5]等人提出基于控制限策略的订购策略;考虑到供应不确定性与需求的非平稳性，Lu Hui[6]等人采取“两阶段”的处理决策，在假定物料充足的情况下，制定原材料需求计划。

考虑到产量柔性的存在，实际供货量可能多于或少于订货量，因此，本文引入风险因子反映供货量的波动特征，然后运用SARIMA模型预测未来24周里每周的供货商应满足的订货量，最后以保障生产稳定性和原材料订购结构优化为目标，建立目标规划模型，制定每周最经济的订购策略。

1 问题分析

1.1 问题描述

已知某生产企业的[n]家供应商在过去五年里的供货特征，该企业每年按48周安排生产，需提前制定24周的原材料订购计划，其每周产能为[C]万立方米，每立方米产品需消耗A类原材料[WA]立方米，或B类原材料[WB]立方米，或C类原材料[WC]立方米。该企业应至少选择多少家供应商才能满足未来24周的原材料订购量。

假设条件设定如下：

⑴ 企业生产的重要性仅由供应商的供货实力、稳定性所决定，不考虑企业管理者等主观因素;

⑵ 假设各供应商供应的各类原材料的质量等因素之间不存在差异性;

⑶ 固定订货周期，每月月初可进行订货。

1.2 符号说明

问题描述和目标函数计算过程中所用到的符号定义详见表1。

2 建立SARIMA模型

时间序列[SARIMA（p，d，q）（P，D，Q）]模型结构中，[p]为自回归项数，[q]为移动平均项数，[d]为差分次数，[P]是季节自回归阶数，[Q]是季节移动平均阶数，[D]为季节差分次数。[SARIMA（p，d，q）（P，D，Q）]模型适用于具有季节性、趋势性和周期性的平稳数据序列。

根据该企业的[n]家供应商在过去5年里的供货特征，以[n]家供应商每周供货量总和作为纵轴，以时间为横轴，得到每周总供货量的时间序列图。

通过分析总供货量的时间序列图，可以发现供应商的供货具有季节规律性，因此可以采用ADF（Augmented Dickey-Fuller）检验方法，先对数据进行平稳性检验。

通过分析检验结果，在90%、95%和99%的置信度下，当检验统计量的值均小于对应的临界值时，就可判断序列是平稳的，可以建立SARIMA模型。

本文使用AIC准则来评价选取最优的SARIMA模型。AIC准则是拟合精度和参数个数的加权函数，使AIC函数达到最小的模型被认为是最优模型。

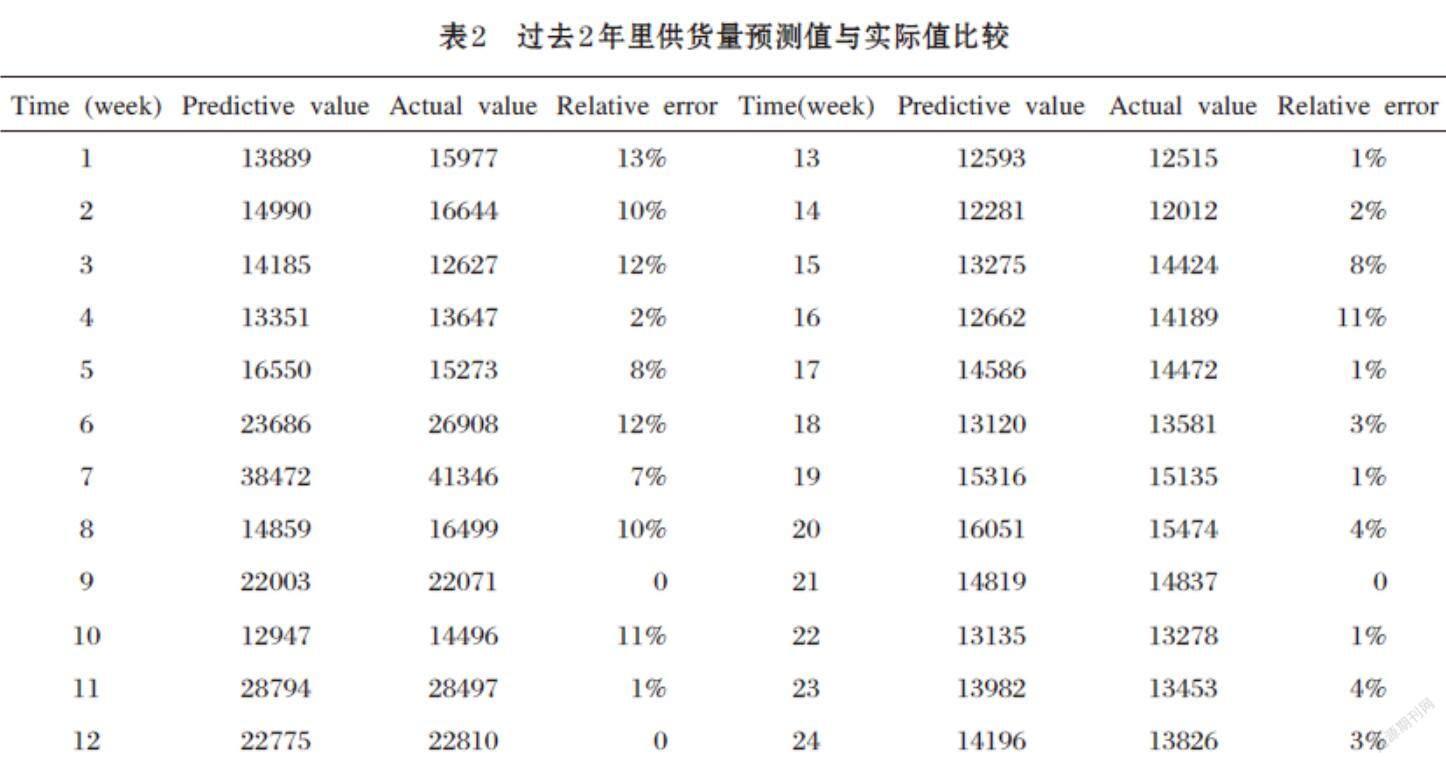
利用选取的最佳预测模型对该企业过去两年的数据进行预测，然后与实际数据进行对比，检验模型的预测效果，预测值与实际值的拟合效果如图1所示。

从最佳模型的拟合效果图1和表2可以看出，整体上的拟合值与实际值之间的差距非常小，相对误差小于12%，模型的拟合效果较好。

SARIMA模型的预测

在模型预测验证精确有效的基础上，可进一步对该企业在未来24周的每周订购量值进行预测，结果如图2所示，然后根据预测得到的每周应满足的订购量值，合理地制定该企业最经济的订购策略。

3 建立目标规划模型

设[A，B，C]三种原材料的供应商的供货矩阵分别[QA，QB，QC]，其中，[QAia]表示第[i]周提供A类原材料的第[a]家供应商;[QBib]表示第[i]周提供B类原材料的第[b]家供应商;[QCic]表示第[i]周提供C类原材料的第[c]家供应商。

选取在满足订购量的前提下，企业所需最少的供应商数量作为目标函数。

[minz=a=1naQAa+b=1nbQBb+c=1ncQCc|QAa，QBb，QCcϵ{0，1}] ⑴

约束条件一：[A，B，C]三类原材料对应的各供应商的供货量限制。

[0<Na≤max {Na|a=1，2，…，na}]  ⑵

[0<Mb≤max {Mb|b=1，2，…，nb}]  ⑶

[0<Kc≤max {Kc|c=1，2，…，nc}]  ⑷

约束条件二：原材料供货量能达到企业每周的订货量。

[a=1naQAaNaβAWA+b=1nbQBbMbβBWB+c=1ncQCcKcβCWC≥C]  ⑸

[a=1naQAaNaβA+b=1nbQBbMbβB+c=1ncQCcKcβC≥Ui]  ⑹

由于实际供货量可能多于或少于订货量，因此，引入风险因子[β]，用以反映供应商的波动特征。

假设[A，B，C]三种原材料的风险因子分别为[βA， βB， βC]，根据过去5年的供货特征，确定[βA， βB， βC]的浮值，其中[βA， βCϵ[0.5，1.9]]，[ βBξϵ0.2，1，ξ=05，5.2，ξ=1]。

综上所述，建立目标规划模型如下：

[minz=a=1nAQAa+b=1nBQBb+c=1nCQCc|QAa，QBb，QCcϵ{0，1}]

[s.t，0<Na≤max {Na|a=1，2，…，na}0<Mb≤max {Mb|b=1，2，…，nb}0<Kc≤max {Kc|c=1，2，…，nc}a=1naQAaNaβAWA+b=1nbQBbMbβBWB+c=1ncQCcKcβCWC≥Ca=1naQAaNaβA+b=1nbQBbMbβB+c=1ncQCcKcβC≥Ui0.5≤βA≤1.9 0.5≤βC≤1.9 0.2≤βBξ≤1，ξ=05≤βBξ≤5.2，ξ=1] ⑺

通过对该模型进行求解，即可得出该企业在未来24周里每周至少应选择的供应商家数量。

4 结束语

本文主要研究在产量柔性条件下确定合理的供货量和订购量，使得企业取得最佳的预期收益。运用SARIMA模型预测该企业在未来24周里每周供货商应满足的订货量，实验结果表明，SARIMA（2，1，1）（2，0，2）12为最佳预测模型，并且预测值与实际值之间误差不超过12%;然后以保障生产稳定性和原材料订购结构优化为目标，建立目标规划模型;最后确定企业最少应选择的供应商数量。本文创新性地提出了风险因子的概念，用以衡量原材料供應商的供货稳定性，使得模型具有良好的鲁棒性，为企业提供了一个构建原材料订购模型的切实可行的有效依据。本文建立的是单阶段订购模型，而如何建立在产量柔性条件下多阶段的原材料订购策略模型是下一步研究的方向。

参考文献（References）：

[1] Arnold， Minner， Bjorn. Raw material procurement with fluctuating prices[J].Production Economics，2009，76（46）：353-364

[2] Zhang Minjie.The construction and application of the simulation model based on selective ordering policy[J].Technological Development of Enterprise，2010，29（9）：5-7

[3] Meiyan Chen. Optimal Ordering Strategies and Financing Strategies Based on EOQ Model[A]. Singapore Management and Sports Science Institute，Singapore， Information Engineering Research Institute，USA.Proceedings of 2019 4th EBMEI International Conference on Economics，Business，Management and Social Science（EBMSS 2019）（Lecture Notes in Management Science，VOL.110）[C].USA：2019，128-132

[4] Zhang Xiaoyue， Dai Wenqiang，Zhou Xiaoyu.Online procurement problem for raw materials with holding cost[J].Systems Engineering，2021，39（3）：153-158

[5] Yang Zhiyuan， Zhao Jianmin， Cheng Zhonghua， Guo Chiming， Li Liying. Optimization model of maintenance and spare parts ordering policy in multivariate degradation system[J].Journal of Shang Hai Jiao Tong University，2021，55：858-867

[6] Lu H，Wang H W， Li F， et al. Integrated scheduling and material supply planning under nonstationary stochastic demand and random supply yield[J].Systems Engineering-Theory & Practice，2019，39（3）：647-658