基于量子计算原理的Shor算法优越性验证
2022-06-20刘安航李浩昱张志华
刘安航,李浩昱,关 佳,张志华,方 恺,赫 丽,沈 军
(同济大学 物理科学与工程学院,上海 200092)
经典计算机需要信息的载体、逻辑操作、状态读出等一系列基本元素. 量子计算机用量子比特作为量子信息的载体,对量子比特进行初始化、操控和读出等,再通过一系列的逻辑操作构成量子算法,从而实现特定的计算目的. 比特是经典计算和经典信息中的基本概念,量子计算和量子信息则建立在类似的概念——量子比特的基础上. 经典计算机中,比特有0和1两种状态,利用0和1构成的比特串编码分别表示不同的信息. 而在量子计算机中,信息单元被称为量子比特,除了可以处于0态或1态外,还可以处于叠加态. 借助叠加态,可以实现利用较少的量子比特储存更多的信息.
Shor算法由P. W. Shor在1994年提出,是针对整数分解问题在量子计算机上运作的算法[1],该算法可以解决如下问题:给定整数N,找出其质因数. 现有的经典算法还无法有效地解决该问题[1-2],因此Shor算法展示了量子计算的优越性. 此外,Shor 算法的存在也直接威胁到经典通讯的Rivest-Shamir-Adleman(RSA)加密算法. 所以关于Shor算法的相关研究一直备受瞩目,2019年Aidan Dang等人详细介绍了优化Shor算法的高阶经典模拟技术,利用检查电路的纠缠特性,有效地将其映射到矩阵乘积状态的一维结构中并对其进行了优化[3];2020年在IEEE第5届计算通信与自动化国际会议上,Vaishali Bhatia等人提出了用Shor 算法破解RSA的高效量子计算技术[4].
目前我国在量子计算领域也颇有建树,2017年中国科学技术大学杜江峰院士团队基于核磁共振系统和绝热量子计算模型在Shor算法中实现了6位数291 311的因式分解[5];2020年,段兆臣等人使用量子点单光子源成功编译了Shor算法[6];2021年,中国科学院量子信息与量子科技创新研究院潘建伟、朱晓波、彭承志等人组成的研究团队成功研制了62比特可编程超导量子计算原型机“祖冲之号”[7].
本文的设计思路来自于近代物理实验课程中的量子密钥分发虚拟仿真实验[8],并参考了一些与量子纠缠和量子保密通信相关的实验[9-13]. 设计出了基于Shor算法的实验,首先将质因数分解问题转换为求函数的周期问题,然后通过拟定已知函数和未知函数,从理论上对这2个函数进行实验与分析,得出实验次数n(该实验次数是指为了获得正确的周期结果所需要的运算次数或者选取次数). 通过实验发现量子方法需要的实验次数仅仅正比于要分解的大数N,而经典计算方法需要的实验次数为nn.因此,由于量子算法的并行性,Shor算法在质因子分解问题中存在显著的优势.
1 实验原理
1.1 量子比特
在量子计算机中,信息单元被称为量子比特,除了可以处于0态或1态外,还可处于叠加态.用|0〉和|1〉表示量子比特可取的状态基矢,单个量子比特可取的值为
|Ψ〉=α|0〉+β|1〉,
(1)
其中,α和β为复数.因为存在约束条件αα*+ββ*=1,量子比特可写成
(2)
其中,θ和φ为实数且-π≤θ≤π,0≤φ≤2π.
1.2 量子逻辑门

1.3 量子并行计算
量子并行性使得量子计算机可以在同一时间计算函数f(x)在多个不同x值处的函数值.对于b位的量子存储器而言,可以同时存储2b个数字(态),在量子力学中,对b个量子位的寄存器的一般态可表示为
(3)
其中,|cb|2表示取得对应值的概率.由于储存了2b个不同的态,使用1次量子逻辑门可以同时改变2b个态的cb值,改变了2b个信息,即为量子并行计算[14].
1.4 量子傅里叶变换
在函数的周期求解问题中,量子傅里叶变换(Quantum Fourier transform,QFT)为
(4)
式(4)表示对任意量子态|x〉做傅里叶变换,得到以波矢k展开的表达形式,其中,k=0,1,…,2b-1.
QFT同样可以构成逻辑门,其QFT门矩阵表示为
(5)
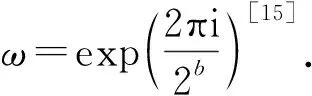
1.5 素数因子分解问题转换为求周期问题
已知大数N,存在唯一的质因子分解N=P1P2,求P1和P2.求解质因子分解问题的步骤包括:
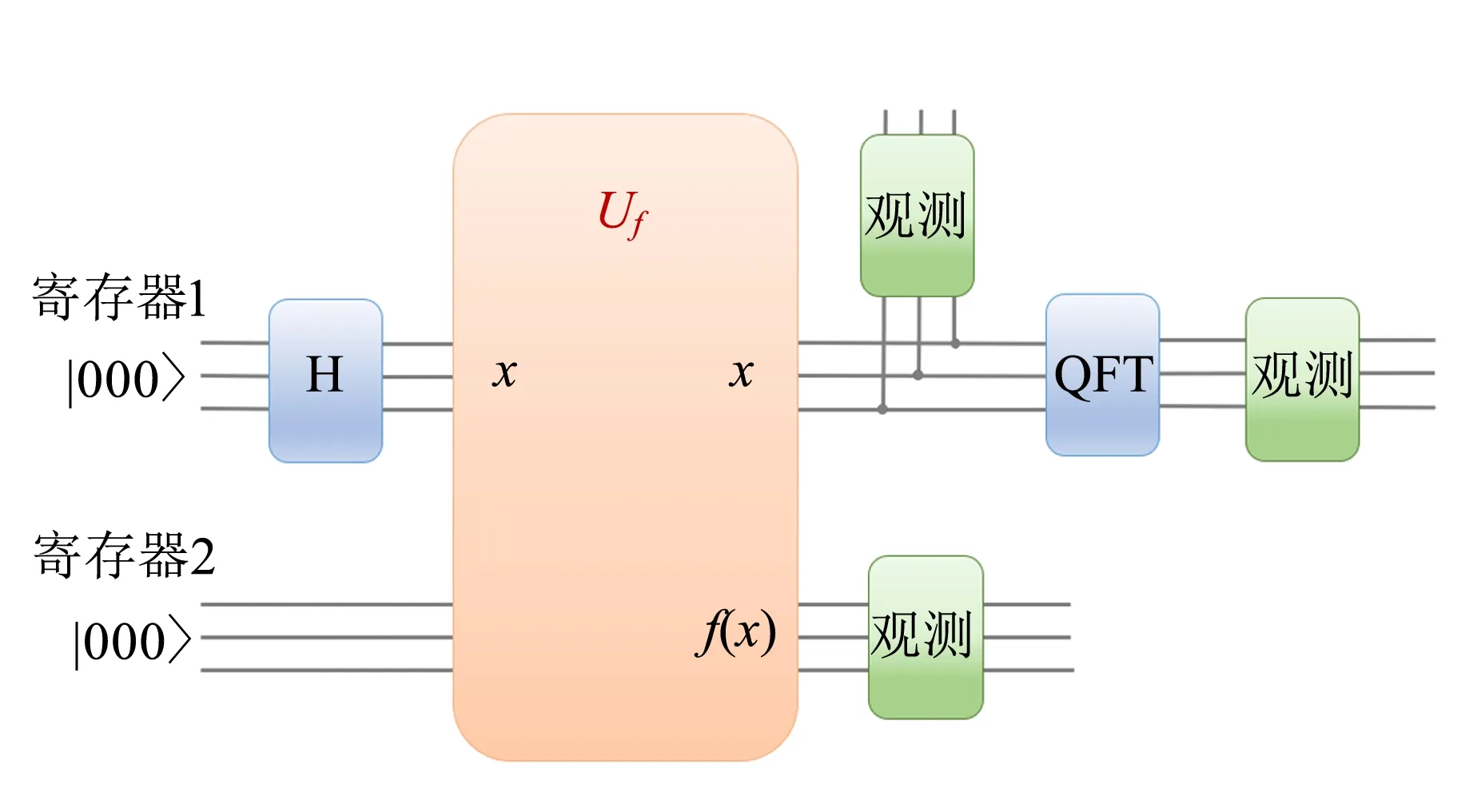
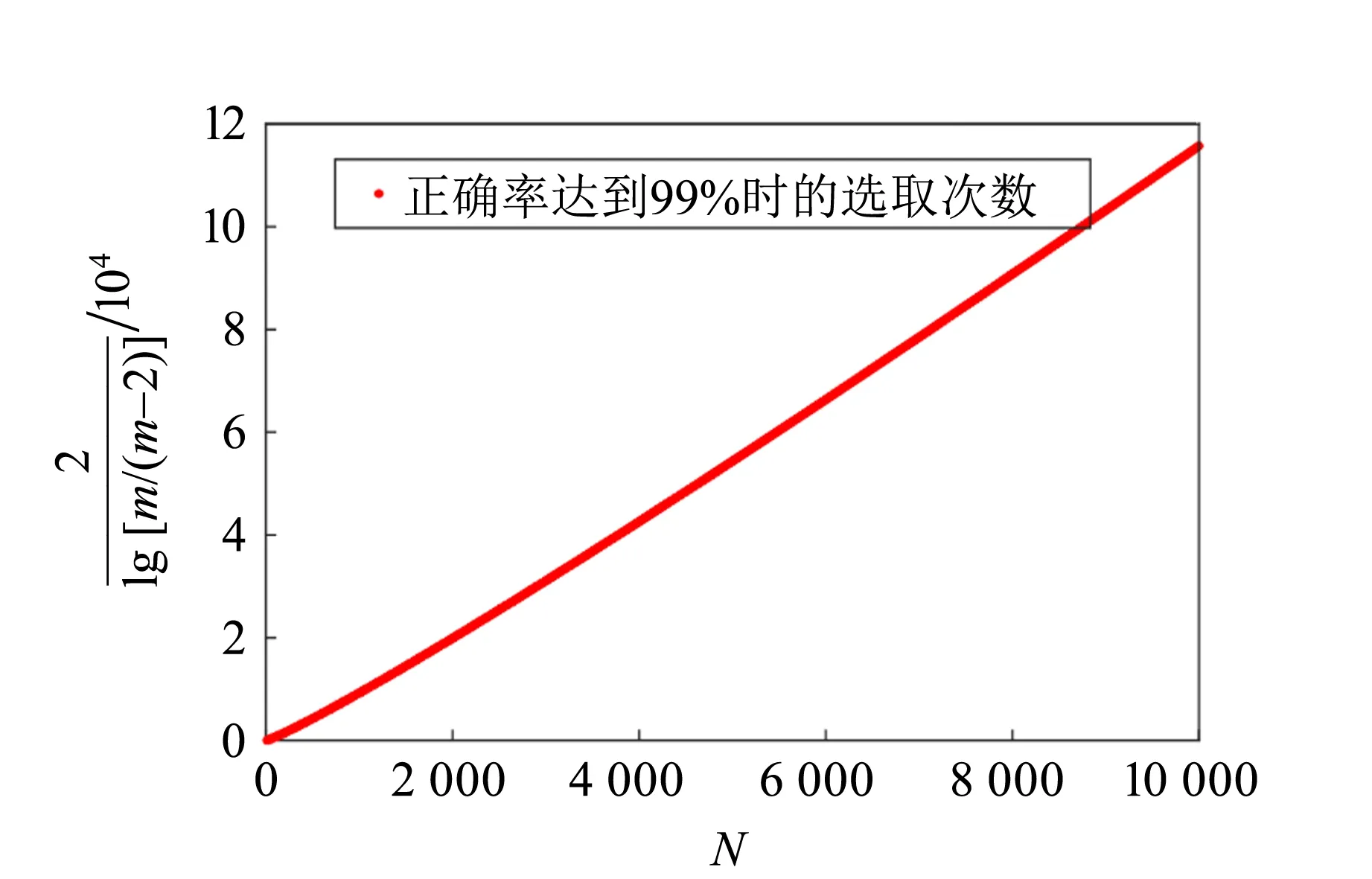
1)随机取大于1的正整数y,使得y 2)若r为奇数,则另取1个大于1的正整数y,继续求r,直到r为偶数. 3)若r为偶数,取x≡yr/2(modN),则x2≡1(modN),进而有 x2-1≡0(modN), (6) 即 (x+1)(x-1)≡0(modN). (7) 于是可设 (x+1)(x-1)=tN=tP1P2=uvP1P2, (8) 其中,t,u,v为正整数,进而有 (x+1)(x-1)=(uP1)(vP2). (9) 式(7)解为 x+1≡0(modP1), (10) x-1≡0(modP2), (11) 即 P1=gcd(x+1,N), (12) P2=gcd(x-1,N). (13) 其中,gcd(x,N)可由辗转相除法求得.因此,若求得大于1的正整数y关于N的阶数r,则可求出P1和P2. 令yx≡z(modN),因yr≡1(modN),则对任意正整数h有 yx+hr≡z(modN), (14) 即以N为模的函数f(x)=yx的周期就是y关于N的阶数r.素数因子分解问题,转换为求函数f(x)≡ax(modN)的周期问题,其中a为大于1的正整数[16]. Shor算法原理的装置图如图1所示,图中的2个寄存器负责储存数字信息. 图1 Shor算法实验装置图 算法流程为寄存器1作为|x〉,在经过H门后储存所有的数字信息,寄存器2经过幺正变换与存储器1中的x建立纠缠并储存函数信息.完成上述流程后得到 (15) 式(15)表明经过变换后,若对初态|ψ0〉进行观测,将得到2b个出现概率相同的态,而当每个态的|x〉确定后,相应的|f(x)〉值也随之确定. 观测f(x)时将使其坍缩为f(x0),由于存在周期性,这时x会坍缩成x0+jT0(T0为周期,j=0,1,2,…,m0-1),需要指出的是此处总的周期数m0=N/T0,如不满足则需做进一步处理[1].这里只讨论m0=N/T0的情况,可得 (16) 由于观测到f(x0)会使得x坍缩成只与正整数j有关的值x0+jT0,此时x与f(x)之间不再存在函数关系(量子纠缠关系),即式(16)可分离(两寄存器之间退相干). 寄存器1在分离后可以表示为 (17) 对寄存器1进行QFT,即经过QFT门可得到 (18) 所以有 (19) 最终可以得到 (20) 此时进行测量,将得到等概率的T0个|km0〉,将其与N进行约分,得到的约分式分母将恰好为待求解的周期T0.可能存在k与T0有公约数的情况,分式可继续约分,这一情况将在第3部分进行讨论. (21) 经典计算方法同样可以按照图1装置图进行实验,仅需要在QFT门前对x进行观测. 3.1.1 已知函数 假定已知函数为 (22) 即函数周期为2. 设寄存器1为3位量子比特,即b=3.寄存器2根据f(x)的值设置为1位量子比特.根据式(15)初始化赋予两寄存器纠缠态,对式(15)中的f(x)进行测量,假设得到f(x)=0,由于两寄存器处于纠缠态,此时寄存器1坍缩为 (23) 对式(23)进行QFT,可以得到的结果为 (24) 实际上在f(x)=1时进行QFT能够得到同样的结果,±号对应f(x)=1和f(x)=0的2种情况,即各有1/2 的概率得到|0〉或|4〉,当得到|0〉时,应舍去,当得到|4〉时,根据 (25) 可得最终周期为2. 3.1.2 未知函数 在实际的质因数分解中,已知条件仅为函数存在周期.假定函数周期为T=16,选择b=6,即N=26=64.进行QFT,可以得到结果为 (26) 在所有的f(x)值下进行QFT都能得到相同结果,即等概率得到以上的T个解,注意T为未知量,需要多次测量来确定T的实际取值,该计算将在3.2节中展开.对所得数据进行处理运算,约分得到下列值 (27) 由式(27)可知有些值与周期并不相符,可推断在测量次数较少时,并不能正确分辨待测定的周期值.所以需要多次测量,并选取最大的分母,作为最终的周期值,即16.由此可见该算法并不能在单次测量中得到100%正确的周期值. 3.2.1 经典计算方法 经典计算方法的运算流程为:在通过Uf门后,直接观测x和f(x)的值.假定函数周期为T,由于x与f(x)之间存在纠缠关系,多次重复观测可发现,当观测到相同的f(x)时,对应的观测量x之间的差值必定是T的整数倍.这样观测相同的f(x)值下x之间的差值,取最小值作为周期T. 在经典计算方法中使正确率达到99%的运算次数,可以分为2个步骤: 1)选择相同的f(x),由于N=mT,则单次实验的选取成功率为P(1)=1/m. 由于m不能确定,将m用N来表示,运算结果如图2所示,其中横坐标为要选取的大数N,纵坐标表示在对数坐标下的选取次数,红色点是对应大数N下计算得到的运算次数在坐标空间内的点,对应的选取次数在对数坐标下与N基本呈正相关,当N在104附近时,就需要101.2×105次选取,这样计算量巨大,难以达到要求.如果分别计算两步骤的选取次数,就可以得到2次的选取次数均与N呈正比例关系,即最终的表达式为c0Nd0N(c0和d0均为比例系数).因此,在经典计算方法下,大数质因子分解问题的复杂度为指数级别O(nn). 图2 对数坐标系下选取次数与大数N的散点图 3.2.2 量子方法 根据上面的计算,进行QFT后共存在等概率的T个结果,一定能够保持分母为T值的2个量分别为1/T和(T-1)/T.所以每次测量至少有P=2/T概率得到想要的值.在n次测量后得到该值的概率为 (28) 由于式(28)中的周期并不能事先确定,因此需要选取更大的大数N值.为了保证结果的准确性,需要从理论上分析选取次数与正确率的关系,如图3所示. 图3 运算次数与大数N的散点图 图3中横坐标为选择的大数N,纵坐标为在正确率为99%时需要的运算次数,蓝色圆圈是对应周期下计算得到的运算次数在坐标空间内的点.由图3可知对应的运算次数n与大数N呈正相关.这说明在量子计算方法下,仅需要多项式级别的复杂度O(n)就可以解决大数的质因子分解问题. 将量子计算方法与经典计算方法进行比较,得出在量子算法中分解质因数的复杂度为多项式级别O(n),而经典计算方法中分解质因数的复杂度为指数级别O(nn).因为量子计算具有并行性,即在量子算法中,1个量子门可以对其储存的2b个数据同时进行运算,省去了经典计算方法中逐个进行计算的过程.本实验中,量子傅里叶变换门同时对2b个数据展开运算,直接得到了包含T个数字的等概率的波函数,降低了计算的复杂程度.本文对设计的实验进行了数值上的模拟和计算,验证和解释了Shor算法的运行机制以及量子计算的优越性.2 实验内容
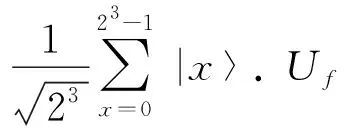
3 实验结果与讨论
3.1 周期测定
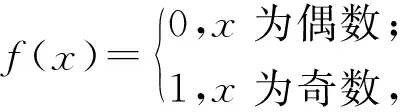
3.2 测量次数的确定
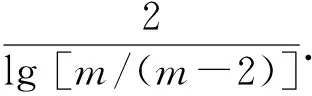

4 结束语
