长寿风险下混合型养老金负债的估值

刘 帅，王传玉，王 奕

(安徽工程大学 数理与金融学院金融系，安徽 芜湖 241000)

目前，世界各国的私人养老金计划就给付方式的不同可以分为三类：一是确定福利计划(DB型计划)，二是确定缴费计划(DC型计划)，三是将DB型计划和DC型计划有效结合而成的混合型计划。三者基本特点的比较如表1所示。DB型计划：养老金计划发起人或管理人向计划参与者作出承诺，保证其养老金收益按事先的约定发放。对计划的参与者承诺了一个固定收益，具有一定的保障性。但是，未对计划参与者建立个人投资账户，而是由计划发起人集体投资，统一管理，参与者不享有超额的投资收益。投资选择与投资风险由发起人承担，一旦投资收益无法履行对参与人承诺的保障义务，这对发起人公司就意味着长期负债，面临着偿付能力风险。DC型计划：计划参与者向养老金计划的缴费是确定的，但参与者退休后的福利由投资收益所决定。计划的发起者对计划参与者建立了个人账户，由参与者根据自己的投资选择和风险偏好进行投资，可以获得超额的投资收益，但投资风险由参与者自己承担。但是，当金融市场发生大的波动时，将导致个人账户的资产缩水，参与者退休后的收入将无法得到保障。混合型养老金计划：计划的发起人或者管理人向计划的参与者承诺在其退休时能得到一个固定的收益，同时为计划的参与者建立个人账户进行独立投资。退休后的最终福利由承诺的固定收益和投资收益组成，不仅具有一个固定的保障，而且还可以获得超额的投资收益。但是，房连泉[1]从风险共享机制的角度指出国际上混合型养老金计划在设计、制度、监管等方面较为复杂，可能存在激励冲突。

表1 DB、DC和混合型计划的基本特点比较

随着世界人口死亡率的逐步下降和预期寿命的提高，长寿风险是世界各国养老金机构面临的主要系统性风险之一，各国的养老金计划发起人对计划参与者养老金的支付额也随之增加，面临着偿付风险。因此，为了度量养老金发起人的这一增量资本，长寿风险的评估已成为国内外学者研究的重点。

基于长寿风险的养老保险负债评估的研究中，国外学者Mikkel等[2]研究了具有系统死亡风险的人寿保险合同的评估和对冲问题，利用CIR模型推导了人寿保险负债的无差异价格和风险最小化的对冲策略。Juan等[3]采用综合会计、个人生命周期概况和一般均衡模型对西班牙人口老龄化下的社会保障支出进行评估。Norbert等[4]使用广义的双因素Lee-Carter死亡率模型对未来死亡率预测，并评估微观和宏观寿命风险对资金比率不确定性的影响。Borger[5]应用随机死亡率模型，通过在险价值(VaR)方法，计算了死亡率被低估的长寿风险的偿付能力资本要求。国内学者祝伟等[6]在动态死亡率的框架下运用wang转换的风险定价方法分析长寿风险对个人年金产品定价的影响。韩猛等[7]将破产概率与年金合同定价相结合研究了即期年金保单组未来现金流的分布特征，测算了即期年金保单组的未来现金流，探讨了保单规模和性别对长寿风险的影响。封铁英等[8]利用生命表技术和随机死亡率预测方法，评估农村社会养老保险的长寿风险，并给出了优化制度设计、强化参保人责任、引入市场机制等应对策略。谢琳[9]采用基于有限数据的双随机Lee-Carter模型构建全因素区间估计方法度量长寿风险，从年度基金率和平衡率、长期存量债务和长期平衡率等方面考察中国城镇职工基本养老保险的偿付能力状况。

本文在Dirk等[10]基础上将混合型养老金计划的负债估值纳入长寿风险因素进行理论研究。首先，对混合型养老金的福利机制、金融市场以及长寿风险进行合理的假设与建模。其次，利用伊藤公式和随机微分方程理论知识推导出混合型养老金计划的未偿总负债的估值表达式。最后，对估值表达式进行数值模拟，分析混合性参数、养老基金投资政策中的股权分配比例、股票波动率对混合型养老金计划的未偿总负债估值的影响。

1 模型建立

设置一个基于55个重叠世代组成的混合型养老金计划，假设该计划中参与人员的年龄25～80岁，所有个人在25岁开始工作，65岁退休，且这55个群体是同质的。考虑到长寿风险，混合型养老金计划内生存超过80岁的世代视为长寿世代，计划发起人承担长寿世代的福利支付，假设最大寿命105岁。混合型养老基金在t=0时开始运作，遵循自融资策略，除了初始投资之外，在投资过程中，不追加任何投资，也不从投资中转移资本，这是为了防止计划参与者的投机行为。随着时间的推移，模型中的混合养老基金人口将由越来越少的工作世代组成，直到t=40时，整个混合养老基金人口由退休世代组成。

1.1 福利机制

假设1所有退休的世代最初都在i时获得相同的福利。

(1)

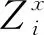
(2)

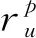
此外，可以通过参数α定义一个连续的养老金合同：若α=0，则养老金合同具有DB计划的特点，因为受益人的业绩是无风险回报。若α=1，则养老金合同具有DC计划的特点，因为受益人收到养老基金资产的实际回报。若α∈(0,1)，则养老金合同是一个由DB和DC元素组成的混合型计划。

由式(2)得

(3)

1.2 金融市场

假设混合型养老基金在基金存续期间[0,T]时投资于只含有两种交易资产的金融市场上运作：一种是股票S，另一种是无风险债券B。

假设2 在风险中性定价测度p下，股票的价值演变满足随机微分方程：

(4)

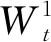
假设3在风险中性定价测度p下，无风险债券的价值演变满足随机微分方程：

dBt=rtBtdt。

(5)

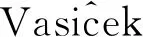
(6)

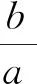
(7)

由式(7)可知：

(8)

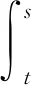
假设5混合型养老基金以β比例投资股票，1-β比例投资无风险债券。混合型养老基金的资产价值变化如下：

(9)

给定风险中性测度p，应用伊藤公式，Xt在[0,t]上的对数回报表示为

(10)

由式(10)可知：

(11)

1.3 长寿风险

Antolin[12]定义长寿风险是指由于未来死亡率的实际值与预期值不一致而给保险公司和养老金机构带来的可能损失。因此，对于未来死亡率的研究成为长寿风险分析的基础。Lee等[13]最早提出了一个简洁的动态死亡率模型，构造t时刻年龄x世代的中心死亡率mx,t得：

ln(mx,t)=αx+βxkt+εx,t,

(12)

式中，αx是与年龄相关的常数;kt是时间趋势;βx是对数中心死亡率对时间趋势的敏感性,随着年龄的增长而降低;εx,t是误差项。

假设6 中心死亡率在一年内是恒定的，即mx+s,t+s=mx,t(0≤s≤1)。所以一年的死亡概率qx,t满足

qx,t≈1-e-mx,t,

(13)

则一年的生存概率px,t为

px,t≈e-mx,t,

(14)

累积生存概率为

(15)

式中，ipx,t表示年龄x的世代在t时刻生存到i时刻的生存概率。

Olivieri[14]以期初年金精算现值的方法对长寿风险度量。在该混合型养老金计划中，对生存超过80岁的世代(最大105岁)，按照1单位的期初年金的方式给予混合型养老金福利。通过计算，该年金福利在t时刻的现值为

(16)

1.4 未偿总负债

将混合型养老金计划未来支付给参与人的福利的现值看做混合型养老金计划发起人的未偿总负债，引入长寿世代的福利支付，以此来刻画混合型养老金中的长寿风险。模型区分了两种情况：t≥40(既有工作世代也有退休世代)和t>40(只有退休世代)。模型中的关键变量是未偿总负债在时间t的贴现，表示为

(17)

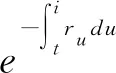
2 混合型养老金负债估值的推导

本节对模型进行推导，确定未偿总负债在t=1,…,55时的未偿总负债的值。混合型养老金计划的负债在时间t时的市场一致性估值可以表示为

(18)

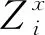
(19)

考虑到混合型养老金的福利是期间收益，运用Geman等[15]提出的数值不变性原理的测度转换方法进行推导，将期望从风险中性的概率度量p转换为远期风险调整度量pi，其中使用到期日i的零息票债券作为数字。推出了在远期风险调整pi下的期望，并且获得了混合型养老金负债估值的表达式(证明见附录)。

命题1 长寿风险下混合型养老金在t时刻的估值表达式：

(20)

式中，H(i-1,i)表示为

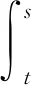
η(u,i)=ρβσs-σ(u,i)

γ(u,t,i)=σ(u,t)-σ(u,i),

(21)

J(i-1,i)表示为

(22)

Y(t,i-1)表示为

(23)

3 数值分析与启示

3.1 数据来源

人口死亡率数据选取了比利时2010～2018年的人口总死亡率水平(见表2)，这是因为《安联全球养老金报告》指出瑞典和比利时的养老金系统是最佳的，而比利时的养老金体系中包含了混合型养老金计划，计划参与人工作40～45年，65岁退休并开始获得养老金福利，这更符合本文模型的假设。其中对工作世代(25～64岁)、退休世代(65～79岁)、长寿世代(80～105岁)分别取死亡率平均值作为各个世代的死亡率水平，忽略性别因素。随机利率模型参数来自Brennan等[16]的数据(见表3)。利率的长期均值为0.0315/0.63=0.05。初始利率水平被认为等于利率长期均值水平，以抵消利率系统性增减的影响。

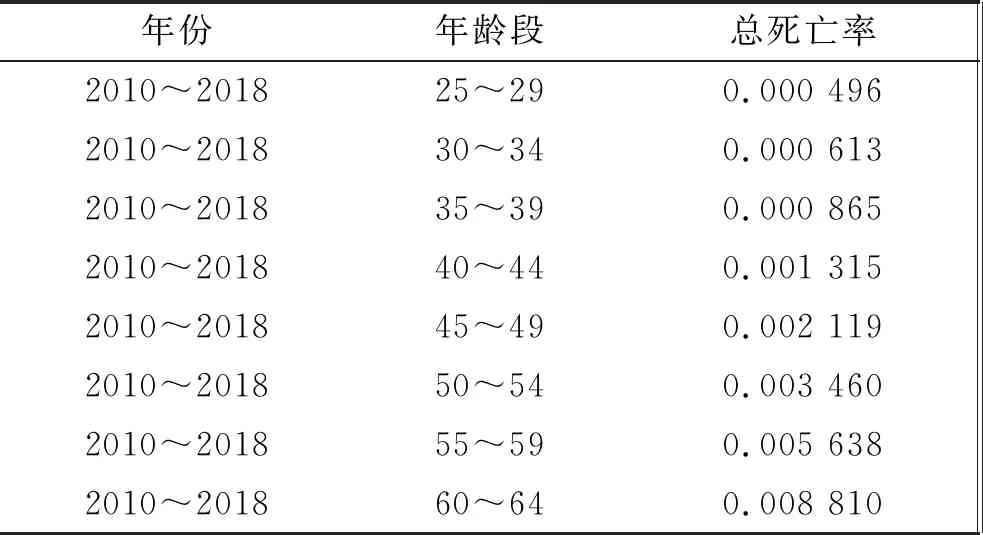
表2 比利时2010～2018年人口死亡率

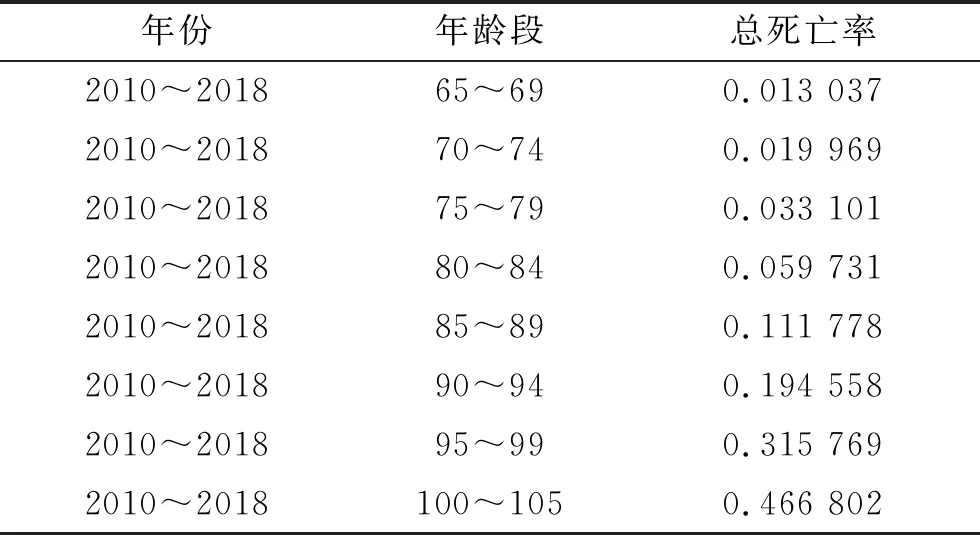
年份年龄段总死亡率2010～201865～690.013 0372010～201870～740.019 9692010～201875～790.033 1012010～201880～840.059 7312010～201885～890.111 7782010～201890～940.194 5582010～201895～990.315 7692010～2018100～1050.466 802

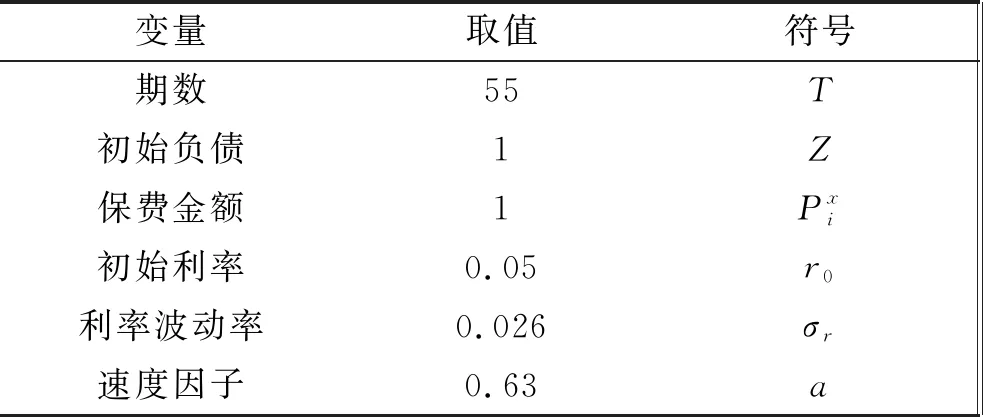
表3 相关参数

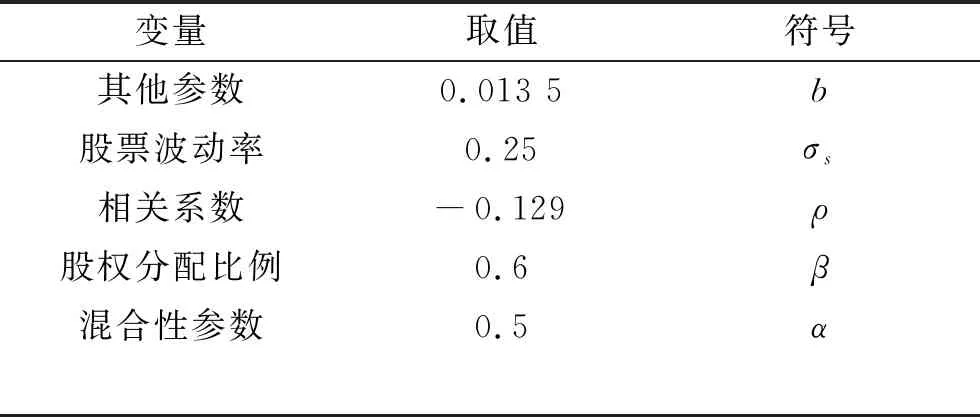
变量取值符号其他参数0.013 5b股票波动率0.25σs相关系数-0.129ρ股权分配比例0.6β混合性参数0.5α

3.2 数值模拟

根据理论估值表达式(20)，将上述参数值带入计算，运用Matlab软件进行数值模拟分析，分别比较了未考虑长寿风险和考虑长寿风险情况下混合性参数α、股权分配比例β、股票波动率σs对未偿总负债的影响，数值模拟结果如图1～6所示。

3.3 讨论与启示

通过比较图1、2可知，第一，混合型养老金计划在运作前50期，长寿风险下的未偿总负债比未考虑长寿风险的未偿总负债估值大约低125个单位。不同世代在考虑死亡率因素后，其每个世代的人数都有所降低，计划发起人不承担死亡人数的福利。在运作后5期，长寿风险下的未偿总负债比未考虑长寿风险的未偿总负债估值大约高30个单位。考虑长寿风险下，混合型计划运行周期期末时存在长寿世代，计划发起人仍然需要对其支付混合养老金福利。第二，混合型养老金计划的未偿总负债值与混合性参数α之间呈负相关。这是由于α的增加使混合型方案中的DB型计划占比逐渐减小，计划发起人承诺的福利随之减小，未偿总负债减少。第三，混合性参数α随着时间的变化对混合型养老金计划的未偿总负债的影响程度逐渐减弱。因为随着时间的推移，混合型养老基金到期日的时间缩短，导致资产回报波动周期缩短。

通过比较图3、4可知，股权分配比例β对未偿总负债估值的影响与混合性参数α一致；混合型养老金计划的未偿总负债值与股权分配比例β之间呈负相关，因为混合型计划中的DC型部分的投资账户是由个人自主投资的，自负盈亏；混合型养老基金资产的风险与股权分配比例呈正相关，投资股票的比重越高，资产风险越高；β=1时，即完全投资于股票，混合型养老金计划在长寿风险下的未偿总负债相较于未考虑长寿风险下的未偿总负债在运行中期有小幅向上的趋势，这是因为股票的波动率较大，一些风险偏好低的投资者开始转变DC型部分的占比，使DB型的占比更高。

通过比较图5、6可知，股票波动率σs对混合型养老金的未偿总负债估值的影响与混合性参数α一致；股票波动率σs与未偿总负债之间呈负相关；不同的股票波动率对未偿总负债的影响在期初有较大的差别，但随着基金运作期的减少而趋于一致；随着股票波动率σs的增加，未偿总负债减少的幅度更大。

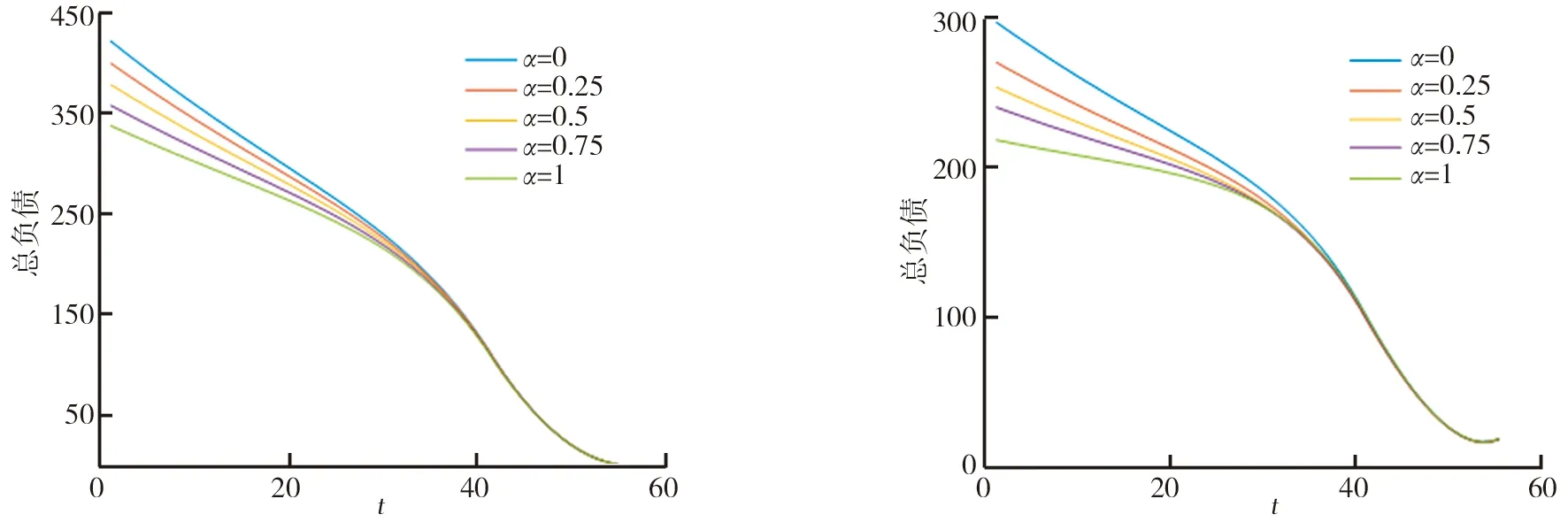
图1 混合性参数α对未偿总负债的影响图2 长寿风险下混合性参数α对未偿总负债的影响

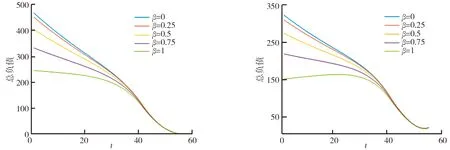
图3 股权分配比例β对未偿总负债的影响图4 长寿风险下股权分配比例β对未偿总负债的影响

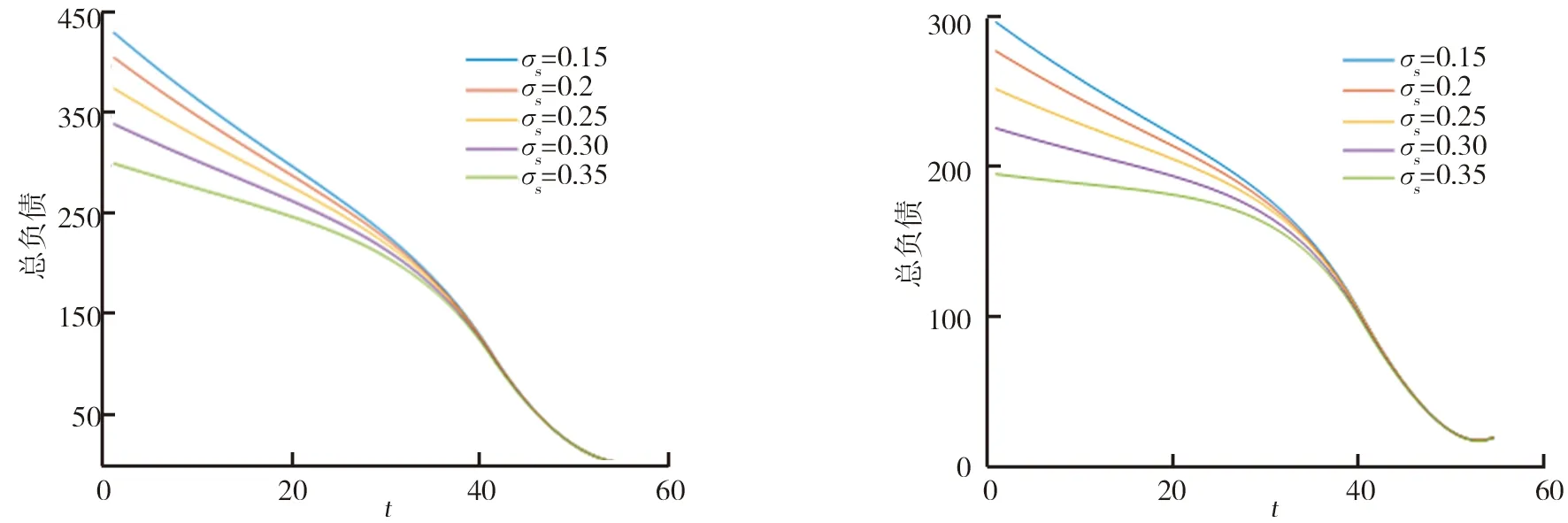
图5 股票波动率σs对未偿总负债的影响图6 长寿风险下股票波动率σs对未偿总负债的影响

本文研究结果的政策启示：对于政府来说，首先，积极稳健地推行渐进式延迟退休年龄政策，鼓励推迟退休和渐进退休，鼓励推迟养老金领取年龄，建立多层次和多渠道的养老金体系。其次，制定混合型养老金混合性参数α和股权投资比例β的合理范围。因为在混合型养老基金中，计划发起人更偏向于较高的混合性参数比例和股权投资比例，这样可以减少定期给付于计划参与者的福利。相反，计划参与者更偏向于较低的混合性参数和股权投资比例，这样可以提高自身的福利领取。因此，政府应制定混合性参数和股权投资比例的合理范围，保护混合型养老金计划的利益双方。对计划参与者来说，混合型养老金计划拓展了居民的养老策略选择，但是计划参与者要结合自身的资产状况、投资偏好、投资期限等理性地选择混合性参数和股权投资比例。对于金融市场来说，首先，金融市场应多渠道为计划发起人资金融资，并积极探索长寿风险证券化的创新性途径。其次，计划发起人可以在金融市场上利用再保险和分红型年金业务来转移部分长寿风险。最后，金融市场要扩大养老基金的投资范围，改变养老金投资收益率低、投资方式单一和投资种类受限的局面，实现养老金的保值增值。

4 总结与展望

本文研究了长寿风险下混合型养老金计划中未偿总负债的市场一致性价值的模型，运用测度转换的方法推出了长寿风险下混合型养老金未偿总负债的封闭表达式，通过数值分析比较考虑长寿风险和未考虑长寿风险下混合性参数、股权分配比例、股票波动率与混合型养老金负债的估值影响。结果显示：混合性参数、股权分配比例、股票波动率与混合型养老金负债的估值都呈负相关。研究得出的相关启示可以为政策或混合型养老金计划的设计提供借鉴。

虽然将混合型养老金未偿总负债估值模型纳入了长寿风险这一系统性风险，但仍有一定的局限性。下一步将考虑通货膨胀风险这另一系统性风险，因为养老金的投资通常是长期投资，通货膨胀影响着混合型养老基金的投资收益与负债水平，计划参与人的福利也会受其影响。因此，为了使混合型养老金计划负债的估值更加精确，更加符合实际，纳入通货膨胀因素是必要的，也具有一定的现实意义。