山区峡谷中大跨度钢桁梁斜拉桥抗风性能试验研究

周霆 李沁峰

摘要：为研究山区峡谷中钢桁架主梁抗风性能，文章以主跨680 m的大跨度钢桁梁斜拉桥为背景，针对钢桁架主梁制作节段模型进行风洞试验，主要研究主梁的关键气动参数，评价其涡振及颤振性能。结果表明：主梁升力系数斜率为正，说明断面具备气动稳定的必要条件。+3°、+5°风攻角时，主梁分别出现了1个扭转涡振区以及1个竖向、1个扭转涡振区，涡振风速区间为20～25 m/s，主梁竖向涡振最大振幅为20 mm;+3°、+5°风攻角时，主梁扭转涡振最大振幅分别为0.074 7°和0.131 8°，均小于规范允许值。+5°风攻角时主梁的颤振临界风速为61.43 m/s，高于颤振临界风速。

[作者简介]周霆（1975—），男，硕士，高级工程师，主要从事大跨度桥梁设计工作。

我国是一个多山国家，山区峡谷地区地形复杂，导致交通基础设施建设远远落后于中部平原地区。随着我国经济社会的不断发展，人民对交通的需求不断增长，在我国西部山区建设大跨度桥梁跨越深切峡谷具有重要的现实意义。但是大跨度桥梁结构柔、刚度小、阻尼低，是风致响应的敏感结构，在强风的作用，容易出现静风失稳和颤振现象，因此须通过专门的抗风分析检验桥梁的风荷载，并保证该桥的抗风稳定性。

斜拉桥跨越能力大、受力合理、便于施工等特点，在西部山区建设大跨度斜拉桥是较好的选择之一。钢桁架主梁结构刚度大、透风率高，目前许多大跨度桥梁均采用此种断面形式，如日本明石海峡大桥、我国的红军赤水河大桥、大渡河大桥、杨泗港长江大桥等。但是，钢桁架截面相对较钝，可能发生涡激振动或颤振[1-3]，影响结构的安全性和乘车舒适性，成为了国内外专家研究的热点。王凯[4-5]、徐爱军等[6]给出了典型山区峡谷桥址处设计风参数选取方法，对比了两种大跨度钢桁架主梁的颤振性能，并提出设置气动翼板或格栅式封闭原主梁的中央开槽的气动措施。徐洪涛[7]、胡峰强[8]给出了山区峡谷中桥梁设计基准风速的选取方法，以及钢桁架主梁的风洞试验模型的设计方法，并对山区大跨度鋼桁梁桥颤振性能进行试验研究。白桦[9]、崔欣[10]等针对窄幅钢桁梁桥的颤振性能进行风洞试验研究，认为抗风缆、中央扣及栏杆可提高钢桁梁的颤振临界风速。

与平原地区不同，山区峡谷地形复杂，传统的桥梁设计风速的选取方法不再适用，可能给桥梁涡激振动及颤振性能的分析带来一定误差。本文基于山区大跨度钢桁梁斜拉桥，计算得到设计基准风速，分析钢桁架主梁的关键气动参数，研究其涡振及颤振性能，为山区峡谷同类桥梁设计提供参考。

1 工程概况

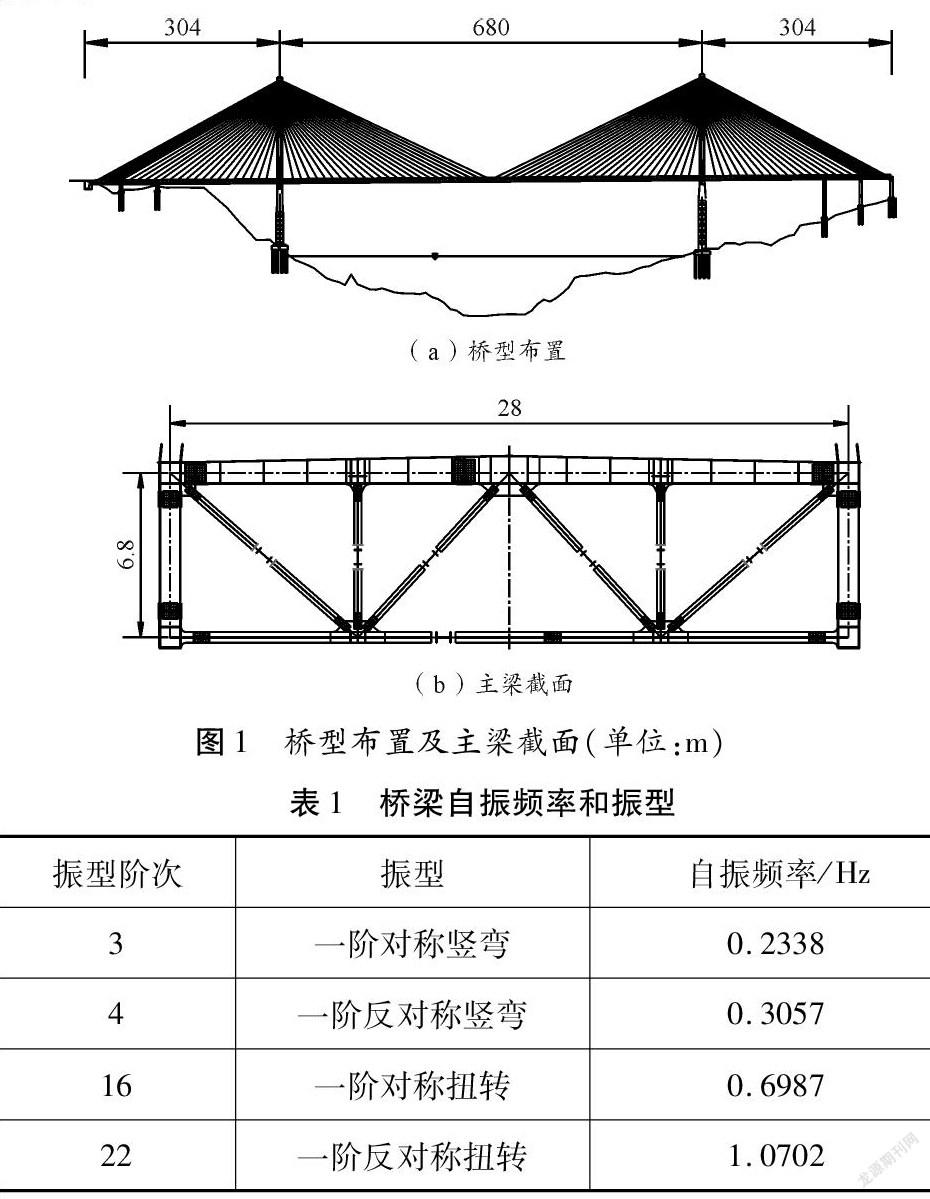
该桥为主跨680 m的大跨度钢桁梁斜拉桥，其孔径布置为（304+680+304） m，桥塔采用混凝土结构，主梁采用钢桁架梁。主跨主梁断面宽25.5 m，高6.8 m。具体桥型布置及主梁截面如图1所示。桥梁结构自振频率及振型如表1所示。

根据JTG/T 3360-01-2018《公路桥梁抗风设计规范》 [11]，按该桥一阶自振频率计算主梁的涡振振幅允许值。主梁的竖向和扭转涡振振幅允许值分别为0.171 m和 0.236°。

2 设计风参数

桥位处于屏山新市与金阳县之间，可以取周边气象站的参考数据，桥位距离规范上列举的气象站宜宾、雷波、昭觉距离较近，可以取风速资料较大者，根据国家气象资料，截止到2015年，可以推算到昭觉百年一遇基本风速为26.6 m/s。桥位地处山区峡谷，不能以常规的风速对数律或者指数律换算得到桥面设计基准风速，可以按照CFD计算获得最大平均修正系数进行折算，折算后该桥主梁高度处设计基准风速为32.45 m/s。桥梁处于山区，可以归为D类地表（表2）。

3 节段模型风洞试验

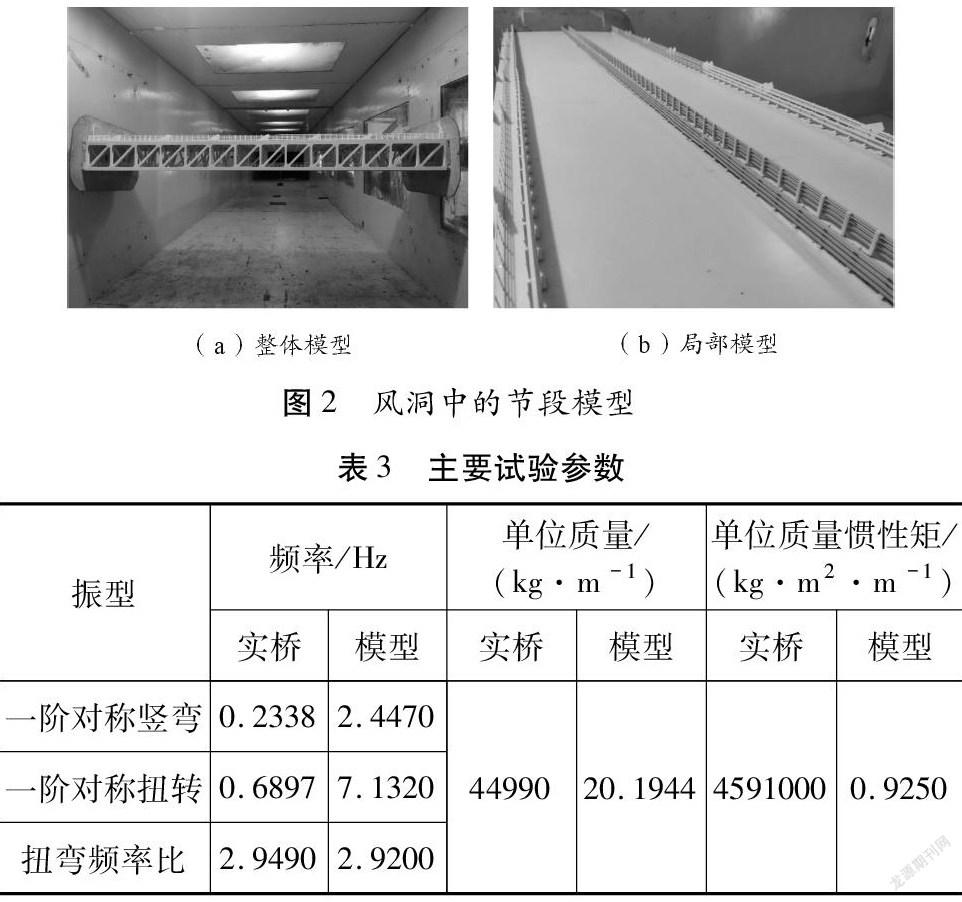
为了解该桥主梁的抗风性能，制作主梁节段模型进行风洞试验。节段模型的几何缩尺比为1∶47.2，模型长2.095 m、宽0.144 m、高0.593 m，长宽比为14.5。主梁采用优质木材及塑料板制作，梁上的内、外侧防撞护栏等附属构件均采用工程塑料且由数控雕刻机制作而成。节段模型通过8根弹簧悬挂于洞壁外的支架上。风洞中的节段模型如图2所示，主要试验参数如表3所示。

4 试验结果分析

4.1 静力三分力系数

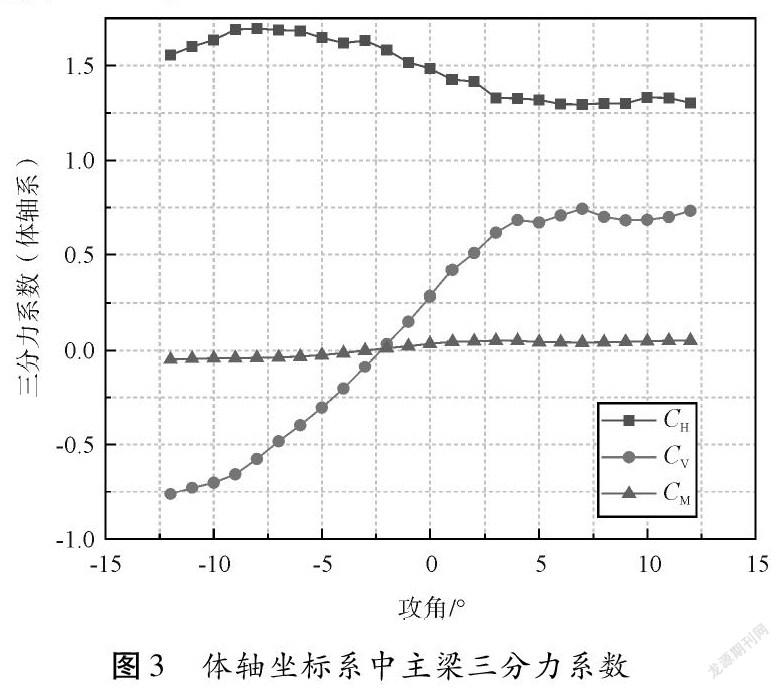
为了分析主梁断面的气动性能，通过风洞试验测量了主梁的静力三分力系数。试验在XNJD-1风洞试验室进行，均匀流场中，风攻角为-12～12°，风速为15 m/s，在体轴坐标系中的试验结果如图3所示。在体轴坐标系中，以水平方向为横轴，竖向为纵轴。从图中可以看出，主梁升力系数斜率为正，说明断面具备气动稳定的必要条件。主梁力矩系数接近于0，受攻角影响较小;0°攻角时主梁的阻力系数为1.486，且阻力系数随攻角变化相对较大，其最大值为1.695，最小值为1.295。

4.2 涡振性能

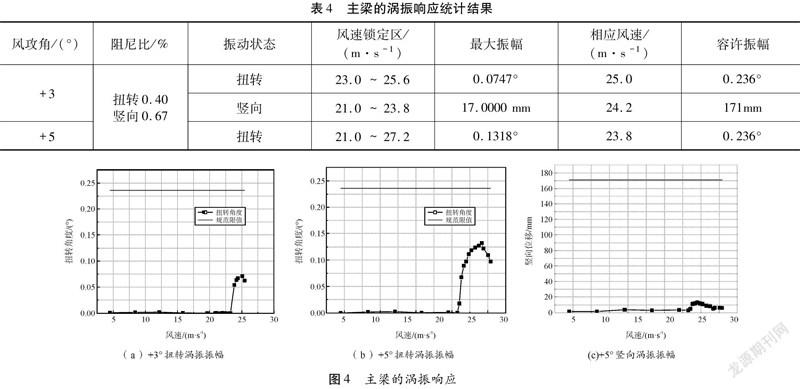
首先，设定桥梁的竖向阻尼比为0.67 %、扭转阻尼比为0.40 %;其次，进行0°、±3°和±5°风攻角下的试验。不同风攻角时，主梁涡振响应如图4所示，表4列出了具体的涡振统计结果。

由结果可知：-5°、-3°和0°风攻角下，主梁没有出现涡振现象;+3°、+5°风攻角下，主梁分别出现了1个扭转涡振区、1个竖向涡振区和1个扭转涡振区;涡振区风速均为20～25 m/s，主梁竖向涡振最大振幅为20 mm，远小于规范允许值;+3°、+5°风攻角时，主梁扭转涡振最大振幅分别为0.074 7°和0.131 8°，小于规范允许值。这说明对于主梁来说，正攻角工况比负攻角工况更加危险，这可能是因为主梁断面较钝，加上栏杆、桥面铺装等的作用，正攻角时主梁尾部形成周期性脱落的漩涡，出现了涡激共振现象，而负攻角抑制了漩涡的脱落，未出现涡激振动现象。

4.3 颤振性能

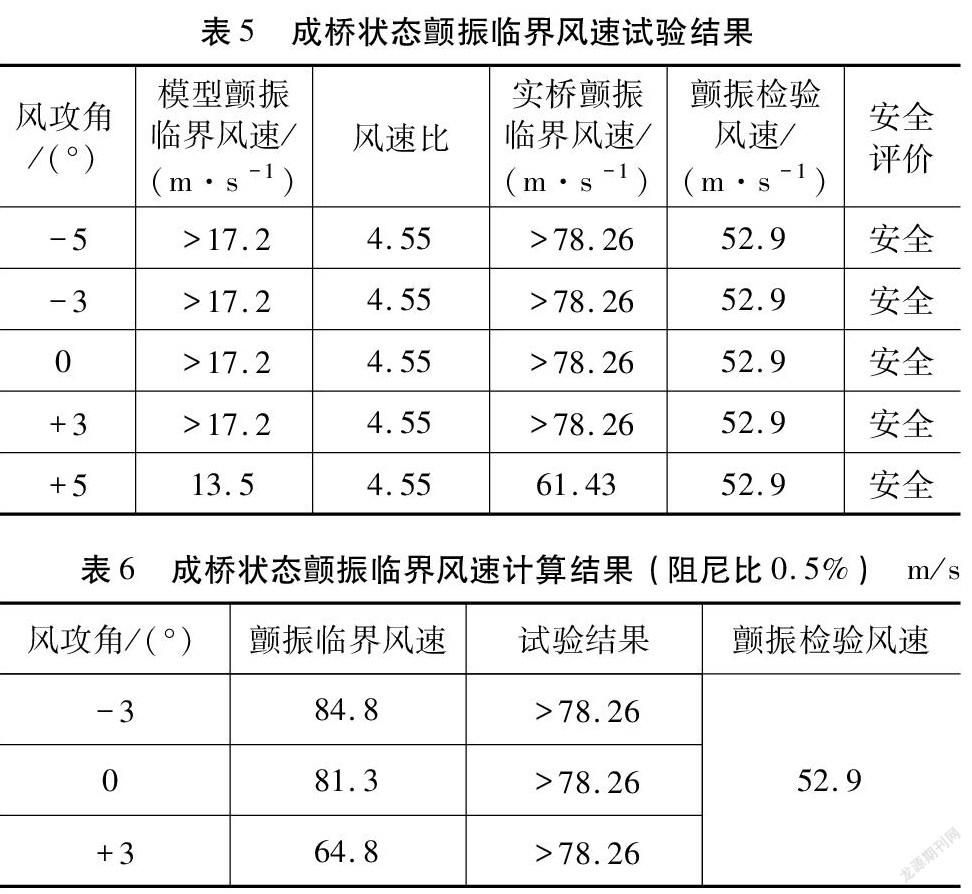
考虑到主梁断面的颤振临界风速对风攻角的敏感性，节段模型动力试验分别在0°、±3°、±5°五种攻角情况下，在均匀流场中进行，桥梁的竖向阻尼比为0.40 %、扭转阻尼比为0.22 %，桥梁主梁成桥状态的颤振临界风速测试结果如表5所示。试验中获得了+5°风攻角下的颤振临界风速为61.43 m/s;在0°、+3°、-3°、-5°攻角时，主梁来流风作用下有较大的静位移，但并未观察到明显风致振动现象，实际临界风速要大于最大试验风速。试验结果表明，大桥成桥状态在0°、±3°、±5°五种攻角下的颤振临界风速均大于该桥颤振检验风速，该桥能够满足颤振稳定性的要求。

桥梁颤振发生形态并不是单纯的竖弯基频和扭转基频相互耦合的形态，它往往是多个振型共同参与的结果，这时发展三维多模态耦合颤振分析理论就显得十分必要的。本文基于三维多模态参与单参数搜索M-S法，编制三维耦合颤振分析程序，对大桥的三维颤振临界风速进行计算，具体计算结果如表6所示。

5 结论

以山区大跨度钢桁梁斜拉桥为背景，通过节段模型风洞试验，研究钢桁架主梁气动参数、涡振及颤振性能，得出結论：

（1） 桥梁主梁高度处设计基准风速为32.45 m/s，桥梁一阶对称竖弯频率为0.233 8 Hz，一阶对称扭转频率为0.698 7 Hz。主梁升力系数斜率为正，说明断面具备气动稳定的必要条件。

（2）+3°、+5°风攻角下，主梁分别出现了1个扭转涡振区及1个竖向、1个扭转涡振区，涡振区风速均为20～25 m/s，主梁竖向涡振最大振幅为20 mm，远小于规范允许值;+3°、+5°风攻角时，主梁扭转涡振最大振幅分别为0.074 7°和0.131 8°，小于于规范允许值。

（3） +5°风攻角下的颤振临界风速为61.43 m/s，且大于颤振临界风速;在0°、+3°、-3°、-5°攻角时，主梁来流风作用下有较大的静位移，但并未观察到明显风致振动现象，实际临界风速要大于最大试验风速。

参考文献

[1] 陈政清. 桥梁风工程[M]. 北京：人民交通出版社，2005.

[2] 管青海，李加武，胡兆同，等. 栏杆对典型桥梁断面涡激振动的影响研究[J]. 振动与冲击，2014，33 （3）：150-156.

[3] 张志田，卿前志，肖玮，等. 开口截面斜拉桥涡激共振风洞试验及减振措施研究[J]. 湖南大学学报（自然科学版），2011，38 （7）：1-5.

[4] 王凯， 廖海黎， 刘君. 山区峡谷大跨钢桁梁桥抗风特性试验研究[J]. 振动与冲击. 2014， 33（19）： 169-174.

[5] 王凯， 廖海黎， 李明水. 基于风洞试验的大跨度钢桁梁悬索桥颤振性能研究[J]. 振动与冲击. 2015， 34（15）： 184-190.

[6] 徐爱军， 王凯， 廖海黎， 等. 板-桁组合式钢桁梁悬索桥颤振稳定性选型研究[J]. 实验流体力学. 2015， 29（4）：52-57.

[7] 徐洪涛.山区峡谷风特性参数及大跨度桁梁桥风致振动研究[D].成都： 西南交通大学，2009.

[8] 胡峰强. 山区风特性参数及钢桁架悬索桥颤振稳定性研究[D]. 上海：同济大学，2006.

[9] 白桦，胡庆安，胡兆同，等. 窄幅钢桁梁悬索桥抗风稳定性能研究[J]. 振动与冲击. 2010， 29（4） ： 155-159.

[10] 崔欣，李加武，刘健新. 窄悬索桥气动稳定性的风洞试验研究[J]. 公路交通科技. 2011， 28（1）： 91-95.

[11] 公路桥梁抗风设计规范： JTG/T 3360-01-2018[S].北京：人民交通出版社， 2018.