基于逻辑回归树耦合熵指数模型的滑坡易发性分区
2022-06-17杨创奇陶攀杨正
杨创奇 陶攀 杨正


摘要:研究合适的县域滑坡易发性分区的方法,对于滑坡的防治有着非常重要的现实意义。鉴于此,基于陕西省延安市吴起县的717个滑坡样本,选取坡度、坡向、高程、平面曲率、剖面曲率、年平均降雨量、距道路的距离、距河流的距离、岩土体类型和NDVI作为影响因子,计算对应的熵指数,构建了基于熵指数的建模数据集。随后,基于建模数据集,耦合熵指数(IOE)和逻辑回归树模型(LMT),建立了IOE-LMT混合分类模型,并绘制了吴起县滑坡易发性分区图。利用多种统计学指标、ROC曲线下的面积(AUROC)和平均绝对误差(MAE)评价分区精度和模型的泛化性能。结果表明:IOE-LMT模型的泛化性能较强(AUROC=0.942),且滑坡易发性分区图的精度较高;研究区内滑坡易发于黄土沟道范围内,并且研究区北部的滑坡易发性明显高于南部。评价结果合理可靠,可为当地的滑坡防治和国土空间规划提供参考。
关 键 词:滑坡易发性分区; 机器学习; 混合分类模型; 空间分析; 延安市; 陕西省
中图法分类号: P694
文献标志码: A
DOI:10.16232/j.cnki.1001-4179.2022.05.021
0 引 言
滑坡是世界上发生频率最高、分布范围最广的地质灾害之一。如何精确地预测滑坡的发生范围是滑坡防治的关键问题。滑坡易发性分区的原理是通过计算后验概率来预测滑坡发生的可能性,是一种预测滑坡的有效方法[1]。现阶段,滑坡易发性分区的评价方法总体分为两大类:一类是知识驱动型方法,例如层次分析法(AHP)[2]、模糊逻辑法[3]、专家打分法[4]等。该类方法依赖人为的先验知识,计算结果容易受到人为因素的干扰。另一类是数据驱动型方法,主要包括统计学方法和机器学习算法。统计学方法被大量应用于滑坡易发性分区的研究中,如确定性指数模型(CF)[5]、熵指数(IOE)[6]、证据权模型(WoE)[7]等,该类模型可以明确地反映滑坡与影响因素之间的联系,计算简便,但过度依赖样本的质量,往往会造成结果错分的现象出现。机器学习算法也被广泛应用于滑坡易发性分区研究中,例如逻辑回归(LR)[8]、决策树模型(DT)[9]、支持向量机(SVM)[10]、人工神经网络[11]等,虽然机器学习算法的计算效率高,但参数的选择对机器学习模型的分类精度影响较大,并且大多数的机器学习算法无法直观地展现分类过程,且计算量大,难以在大范围地区开展分区建模。近年来,结合了统计学方法和机器学习算法优点的混合模型被越来越多地应用于滑坡易发性分区中,并取得了令人满意的效果,如IOE-LR[12]模型、ANFIS[13]模型、PSO-SVM[14]模型等。
雖然诸多学者在县域尺度下利用统计学习方法、机器学习算法和混合模型进行了滑坡易发性分区的研究,但不同区域内的地质条件和环境背景差异较大,并且模型的性能不仅会受到内部参数的影响,同时也会受到由特定研究区域生成的建模数据的影响,所得到的滑坡易发性分区结果的准确性以及合理性也会有所差别。目前,关于黄土高原地区县域尺度下的滑坡易发性分区研究较少,该区域内的各县仍然缺乏区域性国土空间用途管制规划必备的滑坡易发性分区图,探索利用合适的模型开展滑坡易发性分区研究,以及如何提高分区结果的准确性始终是此类地区需要研究的焦点。鉴于此,本文以陕西省延安市吴起县作为研究区,基于野外实际调查的滑坡样本、地质环境背景资料和前人的研究成果,利用混模型的优势,借助于耦合逻辑回归树模型(Logistic model tree,LMT)与熵指数模型,构建了IOE-LMT模型,并对研究区滑坡易发性分区开展研究;最后对分区结果的精度和模型的泛化性能进行定量评估,研究结果可为研究区的滑坡防治工作以及相关区域的地质灾害研究提供参考。
1 研究区概况和数据源
1.1 研究区概况
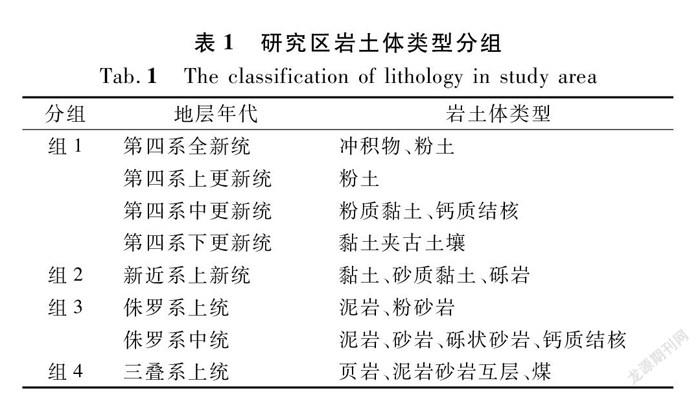
吴起县位于陕西省延安市西北部,地理坐标为东经107°38′57"~108°32′49",北纬36°33′33"~37°24′27",总面积为3 791.5 km2(见图1)。境内河流均属黄河水系,河网密度约为0.86 km/km2,多年地表径流量为1.357亿m3。研究区地貌类型属于黄土丘陵沟壑地貌,高程介于1 203~1 809 m之间,总体呈现出东北高、西南低的趋势。研究区气候类型属于半干旱半湿润温带大陆性季风气候,年平均温度和年平均降水量分别为7.8 ℃和483.4 mm。降水时段主要集中于7~9月,且该时段内的降水量约占全年降水量的62%。根据地层的出露情况,按照地层年代,可将研究区内的岩土体类型分为4组(见表1)。此外,研究区的地层位于整体向西倾斜,倾角介于1°~3°的单斜构造之上,区内地震活动频率较低,且无断层[15]。
1.2 数据源和滑坡编录
1.2.1 数据源和影响因子提取
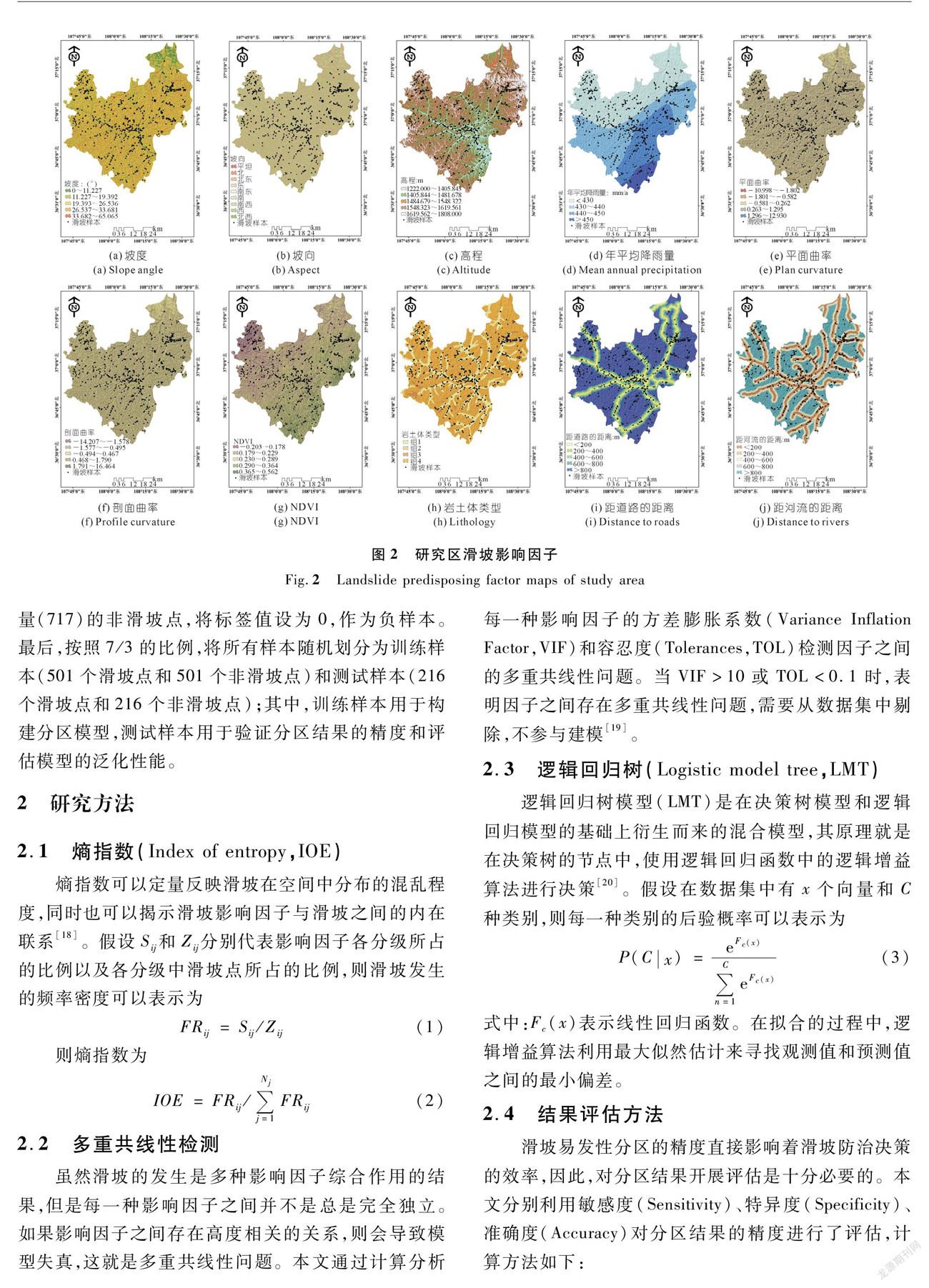
数据源和滑坡影响因子的选择会对滑坡易发性分区的结果造成影响,因此,在开展滑坡易发性分区建模之前,需要阐明研究所使用的数据源[16]。本文在详细参考相关文献以及开展野外调查的基础上,选取了坡度、坡向、高程、平面曲率、剖面曲率、年平均降雨量、距道路的距离、距河流的距离、岩土体类型以及NDVI作为滑坡影响因子。其中,坡度、坡向、高程、平面曲率和剖面曲率因子是基于30 m×30 m分辨率的数字高程模型(Digital Elevation Model,DEM)提取(见图2(a)~(e));根据研究区10 a(2009~2019年)平均降水量数据提取年平均降雨量因子(见图2(f));NDVI因子是利用8 m分辨率的GF-1多光谱遥感影像提取(见图2(g));岩土体类型因子是基于研究区1∶200 000地质图提取(见图2(h));距道路的距离和距水系的距离因子是基于研究区内的路网以及河网矢量提取(见图2(i)~(j))。由于因子图层的分辨率不同会导致模型数据无法输入,因此,每一种影响因子图层的分辨率都被重采样为30 m×30 m。
1.2.2 滑坡编录和制备数据集
滑坡编录是开展滑坡易发性分区研究的基础,滑坡编录图主要包括研究区内滑坡的坐标、类型、规模和特征属性等[17]。根据野外详细调查的数据和历史滑坡资料,研究区内共发育滑坡717处,其中包括681处堆积层滑坡和36处岩质滑坡,滑坡的最大平面面积、最小平面面积和平均平面面积分别为2.6×103,2.7×104,7.7×103 m2。由于研究区内的滑坡总面积仅占研究区总面积的0.04%,因此,为了提升计算效率,利用质心法将全部717处滑坡图斑转换为滑坡点,从而生成滑坡编录图(见图1)。
此外,在构建分区模型之前,首先需要制备模型的输入数据集。本文将全部717个滑坡点的标签值设为1,作为正样本。同时在非滑坡区域随机地生成同等数量(717)的非滑坡点,将标签值设为0,作为负样本。最后,按照7/3的比例,将所有样本随机划分为训练样本(501个滑坡点和501个非滑坡点)和测试样本(216个滑坡点和216个非滑坡点);其中,训练样本用于构建分区模型,测试样本用于验证分区结果的精度和评估模型的泛化性能。
2 研究方法
2.1 熵指数(Index of entropy,IOE)
熵指数可以定量反映滑坡在空间中分布的混乱程度,同时也可以揭示滑坡影响因子与滑坡之间的内在联系[18]。假设Sij和Zij分别代表影响因子各分级所占的比例以及各分级中滑坡点所占的比例,则滑坡发生的频率密度可以表示为
FRij=Sij/Zij(1)
则熵指数为
IOE=FRij/Njj=1FRij(2)
2.2 多重共线性检测
虽然滑坡的发生是多种影响因子综合作用的结果,但是每一种影响因子之间并不是总是完全独立。如果影响因子之间存在高度相关的关系,则会导致模型失真,这就是多重共线性问题。本文通过计算分析每一种影响因子的方差膨胀系数(Variance Inflation Factor,VIF)和容忍度(Tolerances,TOL)检测因子之间的多重共线性问题。当VIF>10或TOL<0.1时,表明因子之间存在多重共线性问题,需要从数据集中剔除,不参与建模[19]。
2.3 逻辑回归树(Logistic model tree,LMT)
逻辑回归树模型(LMT)是在决策树模型和逻辑回归模型的基础上衍生而来的混合模型,其原理就是在决策树的节点中,使用逻辑回归函数中的逻辑增益算法进行决策[20]。假设在数据集中有x个向量和C种类别,则每一种类别的后验概率可以表示为
P(Cx)=eFc(x)Cn=1eFc(x)(3)
式中:Fc(x)表示线性回归函数。在拟合的过程中,逻辑增益算法利用最大似然估计来寻找观测值和预测值之间的最小偏差。
2.4 结果评估方法
滑坡易发性分区的精度直接影响着滑坡防治决策的效率,因此,对分区结果开展评估是十分必要的。本文分别利用敏感度(Sensitivity)、特异度(Specificity)、准确度(Accuracy)对分区结果的精度进行了评估,计算方法如下:
Sensitivity=TPTP+FN(4)
Specificity=TNTN+FP(5)
Accuracy=TP+TNTP+TN+FP+FN(6)
式中:TP和TN分别代表被正确分类的滑坡和非滑坡样本,FP和FN分别代表被错误分类的滑坡和非滑坡样本。
泛化性也是评价滑坡易发性分区方法的重要指标[21]。本文基于受试者工作特征曲线(Receiver Operating Characteristic Curve,ROC)下的面积(Area Under the ROC Curve,AUROC)和平均绝对误差(Mean Absolute Error,MAE)对模型泛化性进行定量评估。ROC曲线的横纵坐标分别为1-特异度和敏感度,曲线下的面积可以通过公式(7)计算。平均绝对误差表示模型对每一个像元的分类结果与真实值之间误差的平均值,MAE值越小,表示模型的分类结果越接近真实值。
AUROC=TP+TN717(7)
3 结果分析
3.1 因子筛选结果
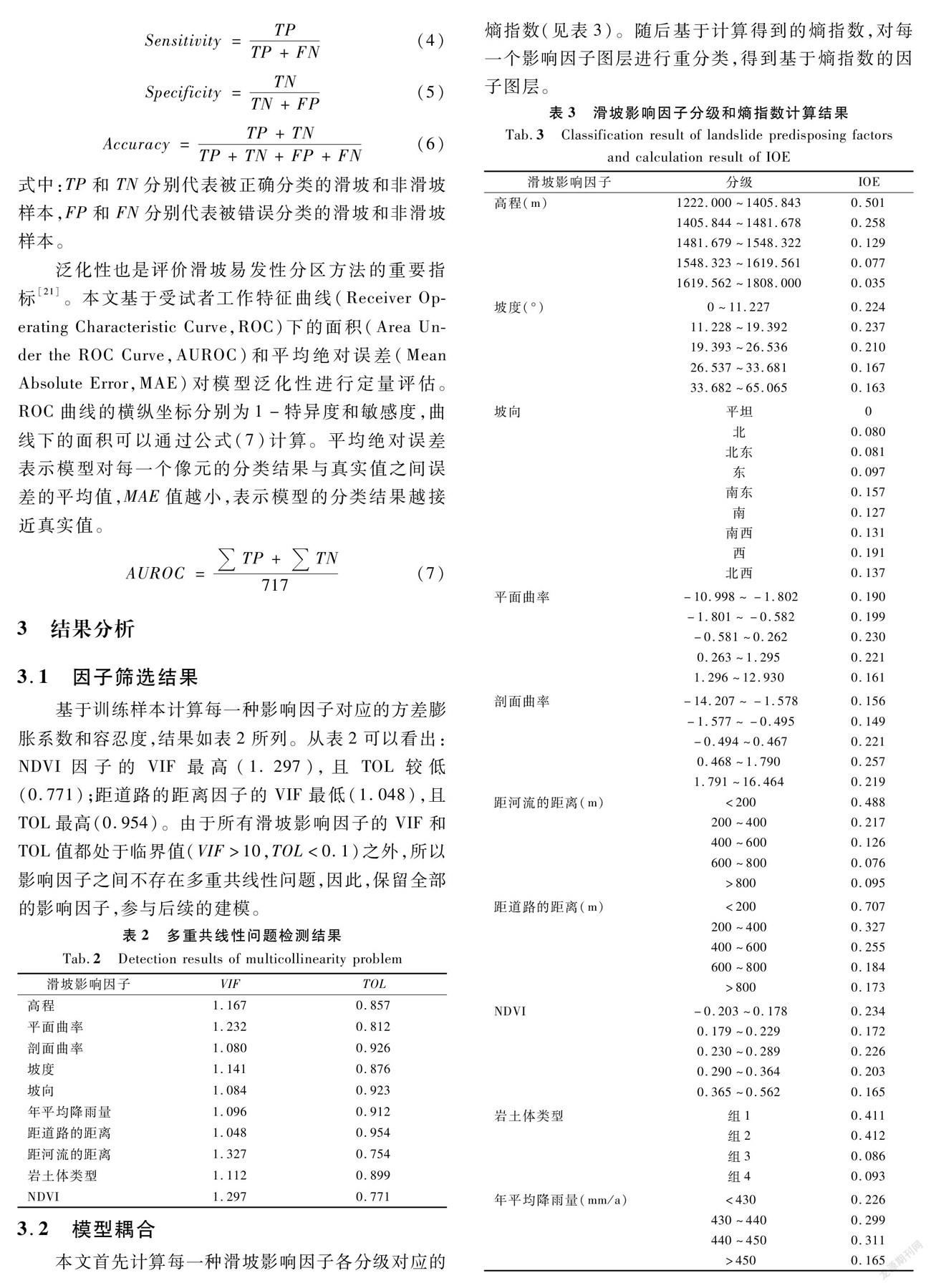
基于训练样本计算每一种影响因子对应的方差膨胀系数和容忍度,结果如表2所列。从表2可以看出:NDVI因子的VIF最高(1.297),且TOL较低(0.771);距道路的距離因子的VIF最低(1.048),且TOL最高(0.954)。由于所有滑坡影响因子的VIF和TOL值都处于临界值(VIF>10,TOL<0.1)之外,所以影响因子之间不存在多重共线性问题,因此,保留全部的影响因子,参与后续的建模。
3.2 模型耦合
本文首先计算每一种滑坡影响因子各分级对应的熵指数(见表3)。随后基于计算得到的熵指数,对每一个影响因子图层进行重分类,得到基于熵指数的因子图层。
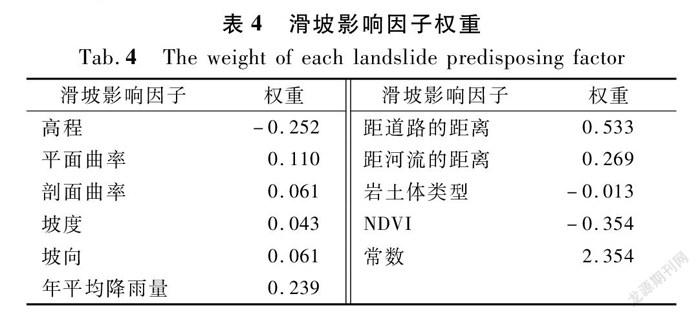
以划分好的样本和因子图层为基础,分别构建基于熵指数的训练数据集和测试数据集。最后将训练数据集输入LMT模型中进行模型耦合,得到各滑坡影响因子对应的权重(见表4),并利用10折交叉验证完成调参,完成IOE-LMT模型的构建。
3.3 滑坡易发性分区
基于训练数据集,利用IOE-LMT模型计算研究区范围内每一个像元的后验概率,输出范围为0~1。该后验概率即为滑坡易发性指数(Landslide Susceptibility Index,LSI),LSI越接近于1说明滑坡发生的可能性越高,LSI越接近于0,表明滑坡发生的可能性越低。为了更直观地显示易发性分区的范围,本文利用自然间断点法将LSI分割为4个区间,分别代表极低易发区(0.001~0.241)、低易发区(0.242~0.393)、中易发区(0.394~0.690)、高易发区(0.691~0.955)。最后基于ArcGIS软件对易发区进行了可视化,如图3所示。研究区内滑坡易发于黄土沟道范围内,并且研究区北部的滑坡易发性明显高于南部。
3.4 分区结果评估
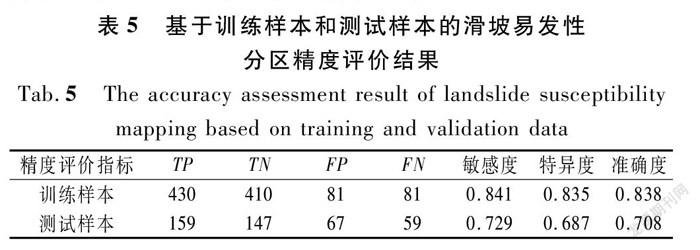
3.4.1 分区结果精度评价
分别基于训练样本和测试样本,计算分区结果的敏感度、特异度和准确度(见表5)。从表5可以看出:滑坡易发性分区的准确度大于0.700,表明滑坡易发性分区结果的精度较高[22];且训练样本和测试样本的敏感度都大于特异度,说明IOE-LMT模型对滑坡的分类能力强于对非滑坡的分类能力。
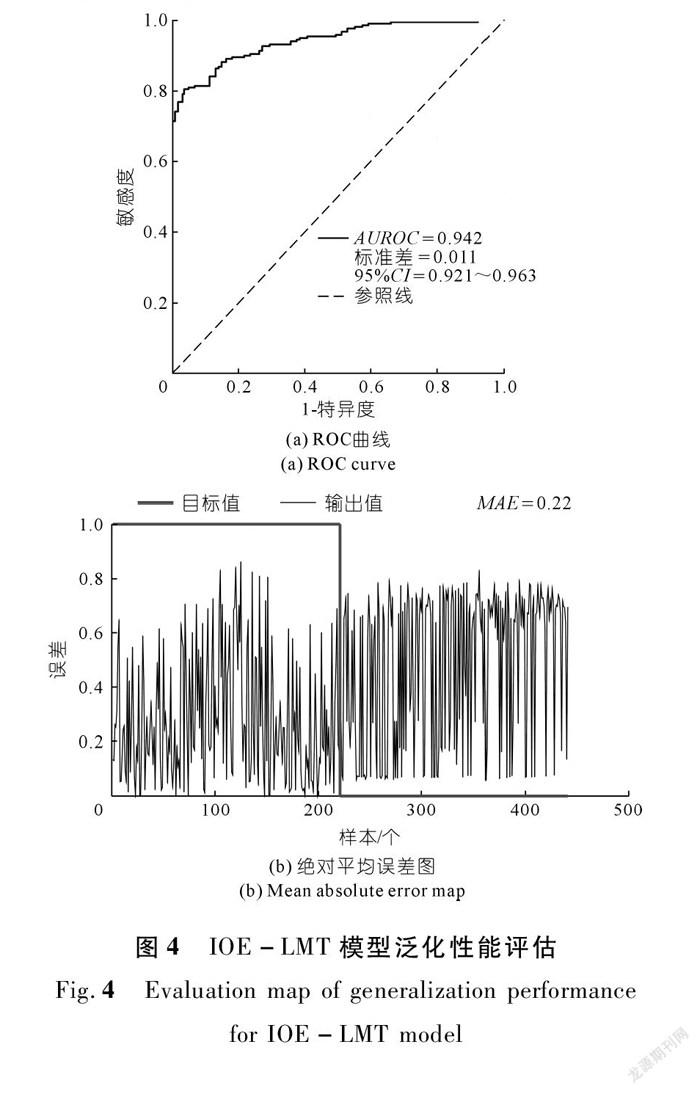
3.4.2 滑坡易发性分区模型评估
滑坡易发性分区模型的泛化性能是评估模型是否适合在其他区域应用的重要指标。本文基于测试样本绘制ROC曲线,对IOE-LMT模型的泛化性能进行了评估。从测试样本的计算结果可以看出:IOE-LMT模型的AUROC值为0.942,标准差为0.011,且模型输出结果的MAE值仅为0.22,表明模型输出的结果与真实值偏差小,泛化能力较强,值得在其他范围进行推广应用(见图4)。
4 讨 论
本文利用熵指数量化滑坡影响因子,构建了基于熵指数的滑坡易发性分区建模数据集,耦合熵指数与LMT模型,建立了IOE-LMT模型,完成了陕西省延安市吴起县滑坡易发性分区,并对分区的结果以及模型进行了评价。虽然本研究得到的结果令人满意,但仍有一些问题值得讨论。
在模型建立之前,对滑坡影响因子进行筛选十分必要。本文仅检测了影响因子之间的多重共线性问题,而没有估算因子对模型的贡献度。但需要注意的是,在LMT模型中,叶子节点的判断策略是通过计算各影响因子的信息增益率实现。而信息增益率本身就反映出了影响因子对模型的贡献程度,如果贡献程度为0,则会被排除[23]。因此,本研究没有单独计算影响因子的贡献度。
熵指数可以反映出滑坡与影响因子之间的内在联系。从IOE的计算结果来看:随着高程的升高,IOE逐渐减小,并且当高程位于1 222.000~1 405.843 m范围内时,IOE最高。造成这种现象的原因可能是由于研究区大量修建公路,造成坡脚开挖,从而导致滑坡发生,而公路所在的高程较低,因而研究区内的滑坡主要分布于低海拔范围内。距道路的距离因子的熵指数计算结果也印证了这一现象,距道路的距离越近,IOE越高。并且结合野外观察发现,IOE反映出的滑坡与影响因子之间的内在联系较为贴近事实,因此,本文利用IOE量化影响因子,可以为提升滑坡易发性分区结果的精度做好基础。
决策树模型是一种经典的机器学习模型,其优点在于可以直观地反映出分类决策的过程,容易解释,但其处理缺失值的功能非常有限,容易出现过拟合[24]。而LMT模型则是以决策树模型为基础,集成逻辑增益算法而构建的,可以很好地规避决策樹模型的缺点。但LMT模型容易受到输入数据质量的影响,而熵指数可以反映出滑坡影响因子与滑坡之间的内在联系,并且利用熵指数量化滑坡影响因子可以统一数据量纲,起到数据增强的作用。因此,利用熵指数作为LMT模型的输入数据构成的IOE-LMT模型,相比于2种基础模型的分类性能更加优秀。此外,本研究中仅使用了一种模型进行滑坡易发性分区,缺乏参照。鉴于此,今后的研究将会在相同的研究区内,同时应用多种分类模型来完成滑坡易发性分区,并对结果和模型进行详尽的评价。
5 结 论
本文以陕西省延安市吴起县为研究区,基于717个实测滑坡数据,首先选取坡度、坡向、高程、平面曲率、剖面曲率、年平均降雨量、距道路的距离、距河流的距离、岩土体类型以及NDVI作为滑坡影响因子。随后利用熵指数量化影响因子,基于因子筛选的结果,构建了建模数据集。耦合LMT模型和熵指数,建立了IOE-LMT模型,并完成了研究区滑坡易发性分区制图。最后,应用多种统计学指标评价结果的精度,以及采用ROC曲线来评估模型的泛化性能。所得结论如下:
(1) 滑坡影响因子的VIF和TOL值均在临界值以外,不存在多重共线性问题,可用于滑坡易发性分区建模。
(2) 滑坡易发性分区的准确度大于0.700,说明分区结果的精度较高,可以为当地的滑坡防治工作提供参考,并且IOE-LMT模型对滑坡的分类能力强于对非滑坡的分类能力。
(3) IOE-LMT模型的AUROC值为0.942,且绝对误差和平均绝对误差均在合理的范围内,表明IOE-LMT模型的泛化性能强,值得推广。
(4) 研究区内滑坡易发于黄土沟道范围内,并且研究区北部的滑坡易发性明显高于南部。
参考文献:
[1] POURGHASEMI H,GAYEN A,PARK S,et al.Assessment of landslide-prone areas and their zonation using Logistic Regression,LogitBoost,and NaveBayes Machine-Learning Algorithms[J].Sustainability,2018,10(10):3694-3714.
[2] MYRONIDIS D,PAPAGEORGIOU C,THEOPHANOUS S.Landslide susceptibility mapping based on landslide history and analytic hierarchy process(AHP)[J].Natural Hazards,2016,81(1):1-19.
[3] 沈玲玲,许冲,王静璞.基于多模型的滑坡易发性评价:以甘肃岷县地震滑坡为例[J].工程地质学报,2016,24(1):19-28.
[4] 张像源,周萌.基于专家评分模型和GIS的滑坡预警分析开发研究[J].中国地质灾害与防治学报,2006,22(2):111-114.
[5] 杨光,徐佩华,曹琛,等.基于确定性系数组合模型的区域滑坡敏感性评价[J].工程地质学报,2019,27(5):1153-1163.
[6] ZHANG T,HAN L,ZHANG H,et al.GIS-based landslide susceptibility mapping using hybrid integration approaches of fractal dimension with index of entropy and support vector machine[J].Journal of Mountain Science,2019,16(6):1275-1293.
[7] 許冲,徐锡伟,于贵华.基于证据权方法的玉树地震滑坡危险性评价[J].地震地质,2013,35(1):151-164.
[8] SOMA A S,KUBOTA T,MIZUNO H.Optimization of causative factors using logistic regression and artificial neural network models for landslide susceptibility assessment in Ujung Loe Watershed,South Sulawesi Indonesia[J].Journal of Mountain Science,2019,16(2):144-162.
[9] HONG H,LIU J,BUI D T,et al.Landslide susceptibility mapping using J48 Decision Tree with AdaBoost,Bagging and Rotation Forest ensembles in the Guangchang area(China)[J].Catena,2018,163(7):399-413.
[10] 韩玲,张庭瑜,张恒.基于IOE和SVM模型的府谷镇滑坡易发性分区[J].水土保持研究,2019,26(3):373-378.
[11] MOAYEDI H,MEHRABI M,MOSALLANEZHAD M,et al.Modification of landslide susceptibility mapping using optimized PSO-ANN technique[J].Engineering with Computers,2019,35(3):967-984.
[12] HANG T,HAN L,CHEN W,et al.Hybrid integration approach of entropy with logistic regression and support vector machine for landslide susceptibility modeling[J].Entropy,2018,20(11):884-900.
[13] CHEN W,POURGHASEMI H R,PANAHI M,et al.Spatial prediction of landslide susceptibility using an adaptive neuro-fuzzy inference system combined with frequency ratio,generalized additive model,and support vector machine techniques[J].Geomorphology,2017,297(15):69-85.
[14] 武雪玲,沈少青,牛瑞卿.GIS支持下应用PSO-SVM模型预测滑坡易发性[J].武汉大学学报(信息科学版),2016,41(5):665-671.
[15] 陕西省地质矿产局.陕西省区域地质志[M].武汉:地质出版社,1989.
[16] TANGESTANI M H.Landslide susceptibility mapping using the fuzzy gamma approach in a GIS,Kakan catchment area,southwest Iran[J].Journal of the Geological Society of Australia,2015,51(3):439-450.
[17] OMID G,THOMAS B,JAGANNATH A,et al.A new GIS-based technique using an adaptive neuro-fuzzy inference system for land subsidence susceptibility mapping[J].Journal of Spatial Science,2018,35(8):1-17.
[18] LIU J,DUAN Z.Quantitative assessment of landslide susceptibility comparing statistical index,index of entropy,and weights of evidence in the Shangnan Area,China[J].Entropy,2018,20(11):868-887.
[19] PADHAN B,LEE S.Delineation of landslide hazard areas on Penang Island,Malaysia,by using frequency ratio,logistic regression,and artificial neural network models[J].Environmental Earth Sciences,2010,60(5):1037-1054.
[20] BUI D T,TUAN T A,KLEMPE H,et al.Spatial prediction models for shallow landslide hazards:a comparative assessment of the efficacy of support vector machines,artificial neural networks,kernel logistic regression,and logistic model tree[J].Landslides,2016,13(2):361-378.
[21] CHEN W,YAN X,ZHAO Z,et al.Spatial prediction of landslide susceptibility using data mining-based kernel logistic regression,naive Bayes and RBFNetwork models for the Long County area(China)[J].Bulletin of Engineering Geology and the Environment,2019,78(1):247-266.
[22] 李航.統计学习方法[M].北京:清华大学出版社,2012.
[23] ABEDINI M,TULABI S.Assessing LNRF,FR,and AHP models in landslide susceptibility mapping index:a comparative study of Nojian watershed in Lorestan province,Iran[J].Environmental Earth Sciences,2018,77(11):405.
[24] WU Y,KE Y,CHEN Z,et al.Application of Alternating Decision Tree with AdaBoost and Bagging ensembles for landslide susceptibility mapping[J].Catena,2020,187(1):104-396.
(编辑:刘 媛)
Landslide susceptibility zoning based on logistic regression tree coupled entropy index model:case of landslide in Wuqi County,Yan'an City,Shaanxi Province
YANG Chuangqi1,TAO Pan2,3,YANG Zheng3
(1.Department of Civil Engineering,Sichuan Vocational and Technical College of Architecture,Deyang 618000,China; 2.Civil Engineering and Hydraulic Engineering School,Shandong University,Jinan 250100,China; 3.School of Water Conservancy Engineering,Yellow River Conservancy Technical Institute,Kaifeng 475004,China)
Abstract:
For landslide prevention and control,it is of great practical significance to study the appropriate method of landslide susceptibility zoning in the county area.In view of this,based on 717 landslide samples collected from Wuqi County,Yan’an City,Shaanxi Province,the slope,aspect,elevation,plane curvature,profile curvature,average annual rainfall,distance from road,distance from river,rock and soil mass type and NDVI were used as an impact factors,and their corresponding entropy indices were calculated to construct a modeling dataset based on entropy indices.Subsequently,based on the modeling dataset,coupled index of entropy (IOE) and logistic regression tree model (LMT),an IOE-LMT hybrid classification model was established to draw a zonal map of landslide susceptibility in Wuqi County.A variety of statistical metrics,area under the ROC curve (AUROC) and mean absolute error (MAE) were used to evaluate the partition accuracy and the generalization performance of the model.The results showed that the generalization performance of the IOE-LMT model was strong (AUROC=0.942),and the accuracy of the landslide susceptibility zoning was high.Landslide in the study area was prone to happen in the loess gullies,and the landslide susceptibility in the north of the study area was significantly higher than that in the south.The evaluation results are reasonable and reliable,and can provide reference for local landslide prevention and land space planning.
Key words:
landslide susceptibility zoning;machine learning;mixed classification model;spatial analysis;Yan 'an City;Shaanxi Province
