基于三有源桥串并联直流潮流控制器的环形双极直流配电网不平衡潮流抑制
2022-06-16何大禄廖建权王强钢
何大禄 廖建权 王强钢
(输配电装备及系统安全与新技术国家重点实验室(重庆大学)重庆 400044)
0 引言
近年来,光伏、储能等直流型分布电源,以及电动汽车、数据中心等直流型负载在配电网中的比例逐渐增加,配电网的“直流特性”越发明显[1-5]。然而,直流型分布式电源或负载接入交流配电网不仅增加了转换环节,而且还可能导致配电网的频率稳定、无功补偿等问题[5]。通过直流配电网连接分布式电源或直流负载,既可减少转换环节,还可增强配电网的电能质量、供电可靠性和供电容量[1-5]。然而,在环状结构的直流电网中,换流站之间可能存在多条线路,使得输电线路的数量大于等于换流站数量,导致线路上的潮流不能仅依靠换流站的电压、功率控制实现有效调节。在这种情况下,直流电网部分线路潮流可能因得不到有效控制而导致线路过载,威胁系统的安全有效运行[6-9]。
为增加直流配电网潮流控制的自由度,许多学者将潮流控制器(Power Flow Controller,PFC)引入直流配电网[10]。根据其与配电网的连接方式,PFC 可分为串联型、并联型和串并联型[11]。其中串联型PFC主要包括可变电阻型PFC 和线间PFC。文献[12-14]提出了三种基于可变电阻器的直流潮流控制方案,其基本原理是通过改变串入线路的等效电阻调节线路潮流。电阻型潮流控制器结构简单、易于控制,但其运行损耗较高且只能单向调节线路潮流。
线间PFC 通过不同直流线路之间的能量交换实现潮流控制[15-18]。在正常工作模式下,线间PFC 通过将一个电容分时串入两条独立的直流线路实现调节潮流,其具有结构简单、成本低等优点,但是会引入电流纹波[11]。并联型PFC 本质上是一个直流变压器,其通过控制直流变压器输出直流电压调节线路潮流。然而,并联型PFC 需承担系统级的电压和电流,成本较高且运行损耗较大[12,19]。文献[20-22]提出了串并联PFC(Series-Parallel PFC,SP-PFC)的拓扑,其输入与直流母线并联,输出与直流线路串联。该PFC 的高低压侧通过高频隔离变压器连接,因此该PFC 只需承受系统的部分功率,成本较低且控制能力较强。
与单极直流配电网相比,双极直流配电网具有多电压接口,接地可靠,且能满足用户的多样化需求[6,23]。然而,由于存在中线电阻,当正、负极之间存在功率不平衡时,正、负极间耦合特性明显[23]。文献[24]分析了双极直流配电网的耦合电压特性,并提出利用直流电力弹簧(DC Electric Spring,DC-ES)抑制不平衡电压。然而,电力弹簧仅能调节不平衡负荷,无法实现系统级的潮流控制。为了实现对单极直流配电网的潮流控制,文献[7]研究了SPPFC 在单极直流配电网中的潮流控制特性,分析了SP-PFC 的工作原理及其控制策略。但若SP-PFC 应用在环形双极直流配电网中,需额外增加SP-PFC 的数量;文献[22]提出了三有源桥串并联直流潮流控制器(Triple Active Bridge Power Flow Controller,TAB-PFC)拓扑,并研究了TAB-PFC 在环形双极直流配电网中的应用,分析了TAB-PFC 的控制模式,但没有验证其潮流控制性能,也未结合环形双极直流配电网的网络特性(如正负极电压的耦合特性、负荷的不平衡、受端电压的不平衡和新能源出力的不平衡)提出TAB-PFC 的控制方法。
为实现环形双极直流配电网不平衡潮流的抑制,本文提出一种基于TAB-PFC 的不平衡潮流抑制策略。相比基于双有源桥的SP-PFC,所采用的拓扑可以减少隔离变压器和高压侧电力电子器件的数量。
此外,为了增强TAB-PFC 在环形双极直流配电网潮流控制的动态性能,本文分析了受端电压、新能源出力不平衡时环形双极直流配电网的正、负极耦合特性,推导了正、负极潮流和线路损耗与不平衡受端电压的关系。在此基础上,推导了恒功率控制下TAB-PFC 输出电压和线路电流的表达式,建立了含TAB-PFC 的环形双极直流配电网的稳态模型和小信号模型。在模型的基础上,引入参数解耦矩阵实现正负极控制环路间的近似解耦。在Matlab/Simulink 中建立了含TAB-PFC 的环形双极直流配电网的仿真模型,并搭建了实验平台。仿真和实验结果验证了TAB-PFC 抑制不平衡潮流及参数解耦矩阵方法的有效性。
1 环形双极直流配电网不平衡潮流分析
1.1 TAB-PFC 的拓扑
TAB-PFC 的拓扑如图1 所示。S1~S12和Q1~Q8是TAB-PFC 的开关管;Cin为PFC 的输入电容;Vdci和Cdci分别为TAB 的输出电压和输出电容;Lfi和Cfi为滤波电感和滤波电容,其中i=1,2;vk1和vk2为TAB-PFC 的输出电压;T 为三绕组隔离变压器,Lσ1、Lσ2、Lσ3分别为三绕组隔离变压器一、二次侧的漏感;Vs、V1、V2分别为送端和受端电压;RL1和RL2分别为正、负极线路的线路电阻。

图1 TAB-PFC 拓扑 Fig.1 The topology of TAB-PFC
此拓扑由三有源桥(Triple Active Bridge,TAB)和全桥变换器(Full-Bridge Converter,FBC)构成。TAB 的一次侧与直流母线并联,一、二次侧通过隔离变压器T 连接,FBC 的输出电压串联连接至直流输电线路中。
1.2 含TAB-PFC 的不平衡潮流分析
TAB-PFC 应用于环形双极直流配电网的示意图如图2a 所示,图中L1~L3表示直流传输线路,Ip、Inu、In分别为正极、中线、负极传输线的电流。TAB-PFC 安装在N1节点的出口处。N1~N3节点的等效电路如图2b 所示,其中N1、N2节点表示电压可控的换流站,N3节点表示功率可控的换流站。

图2 含TAB-PFC 的环形双极直流配电网等效电路 Fig.2 Equivalent circuit of ring bipolar DC distribution network with TAB-PFC
假设N2节点的正、负电压不平衡或N3节点出力不平衡。为分析及控制线路潮流,推导了含TABPFC 的线电流、线路潮流、线路损耗的表达式。
根据图 2b,对其列写节点电压方程及补充方程为

式中各参数表达式详见附录。

各线路上电流I为

式中,E与0 分别为三维单位矩阵与三维零矩阵。
线路损耗为
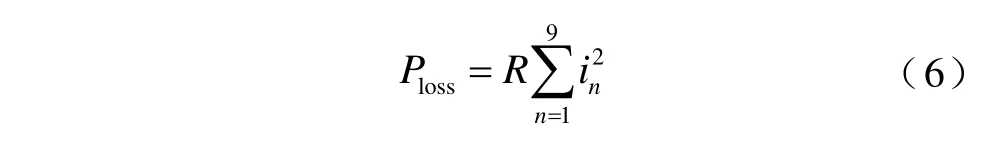
正、负极线路传输的功率P1、P2为

当添加TAB-PFC 时,将式(7)作为约束条件,P1、P2作为给定值控制PFC 的输出电压vk1和vk2。
1.3 不平衡功率对TAB-PFC 的影响
1.3.1 受端电压不平衡对TAB-PFC 影响
为研究不平衡的受端电压对线路潮流的影响以及TAB-PFC 的作用,图2b 的各电路元件参数设置如下:Vs=400V,Rs=0.01Ω,R=0.1Ω,P01=P02=10kW,V01=V02=400V,V2=400V,V1从380V 变化至420V,P1和P2的期望值均设置为10kW。
受端电压不平衡时有、无TAB-PFC 线路潮流对比如图3 所示。当无TAB-PFC 时,线路潮流随受端电压的变化而变化,无法达到期望值;加入TABPFC 后,线路的潮流恒定为期望值。

图3 受端电压不平衡时有无TAB-PFC 线路潮流对比 Fig.3 Comparison of power flow with/without TAB-PFC under unbalanced receiving-end voltage
受端电压不平衡时TAB-PFC 输出电压及有、无TAB-PFC 线路损耗如图4 所示。由图4a 可知,TABPFC 的输出电压vk1和vk2随受端电压V1的变化而灵活调节。由图4b 可知,TAB-PFC 的加入显著降低了受端电压不平衡时的线路损耗。

图4 受端电压不平衡时TAB-PFC 输出电压及有无TAB-PFC 线路损耗 Fig.4 TAB-PFC output and line loss with/without TABPFC under unbalanced receiving-end voltage
1.3.2 新能源出力不平衡对TAB-PFC 的影响
考虑到新能源出力常为光伏,其出力具有很强的不确定性,受天气、时间变化影响较大,典型的光伏小时功率曲线近似为二次曲线[25]。24h 光伏出力及线路潮流如图5 所示。PV 为光伏出力,Pp为正极线路潮流,Pn为负极线路潮流。图 5 中V1=V2=400V,当无TAB-PFC 时,线路潮流随时间增长和光伏出力变化而变化,无法达到期望的功率。而通过控制TAB-PFC 灵活输出vk1和vk2可控制线路潮流恒定,如图6 所示。

图5 24h 光伏出力及线路潮流 Fig.5 24h photovoltaic output power and line power

图6 TAB-PFC 输出电压及线路潮流 Fig.6 TAB-PFC output voltage and line power
2 小信号分析
2.1 含TAB-PFC 的环形双极直流配电网的小信号建模与分析
将式(7)代入式(1)和式(5)可得正、负极线路电流Ip、In,正、负极线路电压vLp、vLn与vk1和vk2间的关系为

式中,a、b、c、d、e,m、n、x、y、z的表达式详见式(A2)与式(A3)。
为便于描述,假设TAB 的输出Vdc1=Vdc2,对于FBC,TAB 输出Vdc可视为恒定值,简化后的TAB-PFC 如图7 所示。
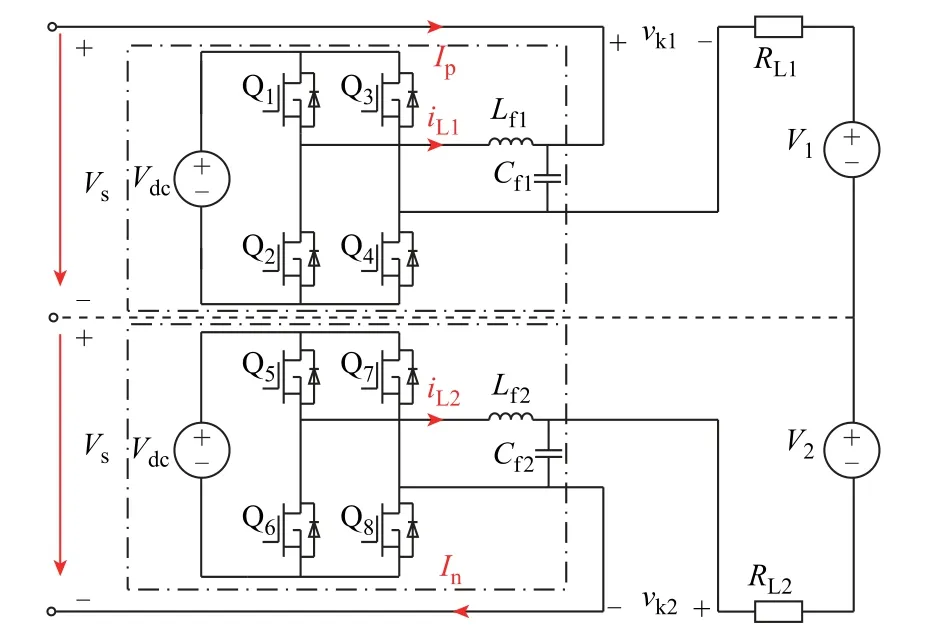
图7 简化的含TAB-PFC 环形双极直流配电网 Fig.7 Simplified ring bipolar DC distribution network with TAB-PFC
将电感电流和TAB-PFC 的输出电压作为状态变量可得到其状态方程为

式中,C1、C2,L1、L2分别为TAB-PFC 正负极的滤波电容和滤波电感;dp和dn分别为正、负极FBC 开关管的占空比;vk1和vk2分别为Vk1和Vk2的暂态值。由式(10)可得含TAB-PFC 的环形双极直流配电网的小信号模型为

根据式(11)可推导控制至输出的传递函数,正极FBC 占空比dp至输出vk1和vk2的传递函数Gpp(s)和Gpn(s)为

其分母表达式为

式中,上标“ˆ”为变量的交流小信号分量。
dp和dn与vk1和vk2的关系矩阵如式(15)所示,该系统为双输入双输出系统,当TAB-PFC 正负极FBC 参数一致时,有Gpp(s)=Gnn(s),Gpn(s)=Gnp(s)。
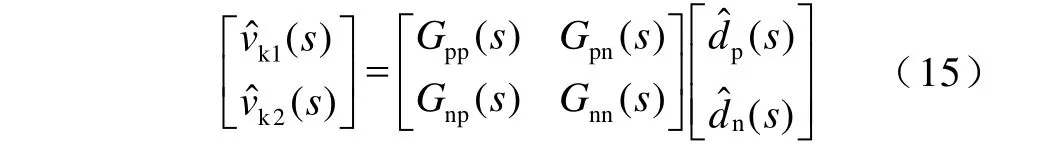
由于Gpn与Gnp的存在,FBC 正、负极的控制回路之间存在耦合关系,解耦网络W可以对其进行解耦。解耦网络将多变量系统分解为两个独立的单回路子系统,各子系统的控制器可以独立设计。该方法的控制系统框图如图8 所示,G表示双极直流配电网中TAB-PFC 输出电压的小信号传递函数,W表示解耦网络的传递函数。分别为所期望的TAB-PFC 正、负极输出电压值,Gcvp(s)与Gcvn(s)分别为正、负极电压环的补偿器传递函数。

图8 FBC 理想解耦网络方法控制系统框图 Fig.8 FBC ideal decoupling network control system block diagram
若使X=GW=diag(1,1),则控制系统的主对角线元素均为1,副对角线元素均为0,此时TAB-PFC正、负极输出电压跟随各自的给定值,互不影响。解耦矩阵为

2.2 解耦控制的实现
式(16)中所示解耦矩阵是理想情况下的形式,但由于W矩阵中各项为传递函数形式,且包含的二阶微分项很容易受到高频噪声的影响,其实现较为复杂,因此本研究引入解耦控制变量k1和k2进行解耦。k1和k2由坐标变换引入,并且使用k1、k2、dp、dn的Jacobian 矩阵来替代理想的W。TAB-PFC 输出电压大信号模型表达式为

故式(9)可写为
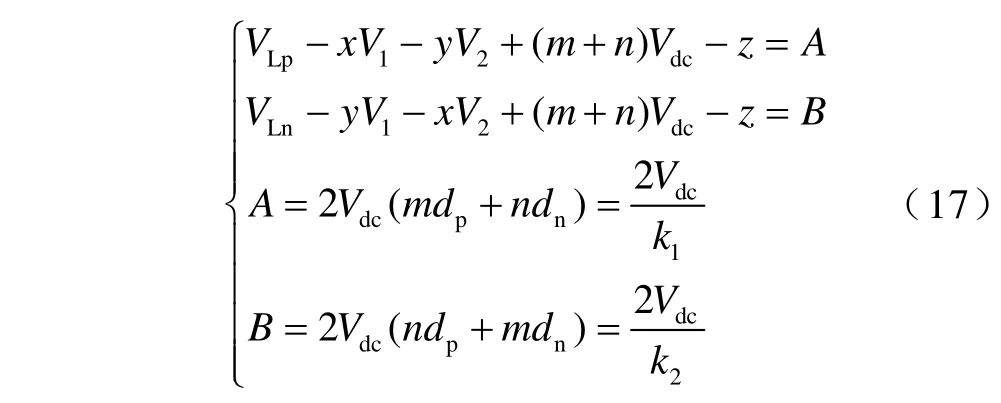
式中,k1和k2为解耦控制变量。式(17)表明,vLp与k2无关,vLn与k1无关。根据式(17),k1和k2满足

dp、dn、k1、k2的Jacobian 矩阵可由式(19)得到。

式中,K1、K2分别为k1、k2的稳态值。根据式(17),K1、K2满足

与式(16)相比,式(19)解耦矩阵中所有元素均为常数,更容易实现。引入解耦网络后的传递函数为
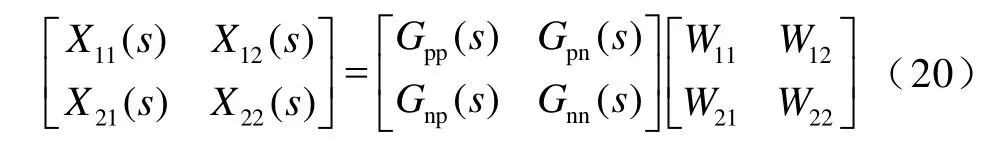
式中,X11(s)、X12(s)、X21(s)和X22(s)为引入参数解耦网络后的传递函数。
若实现了式(16)所示的理想解耦矩阵W,G(s)和X(s)的Bode 图如图9 所示。图9b 表明在引入解耦控制矩阵后,副对角线的增益被大幅衰减,有效地消除了来自其他极的干扰,但其实现较为复杂。

图9 理想解耦矩阵W 下的Bode 图 Fig.9 Bode diagram under ideal decoupling matrix W
若采用式(19)所示的参数解耦矩阵W,G(s)和X(s)的Bode 图如图10 所示,其中W采用额定参数设计。根据式(19)计算得到W11=0.178 2,W12=0.006 8,W21=0.005 2,W22=0.230 0。由图10b,与Gpn和Gnp相比,X12和X21在最高点的衰减量超过15dB,低频幅值在0 以下,实现了近似解耦。式(19)中所示的W简单且易于实现,因此本研究采用式(19)所示的参数解耦网络。

图10 参数解耦矩阵W 下的Bode 图 Fig.10 Bode diagram under parameter decoupling matrix W
2.3 控制器设计
设计FBC 中电压补偿器参数时,电压环的开关频带应比开关频率低,综合考虑稳态性能与动态性能,截止频率一般设计为开关频率的1/10~1/20[26]。基于此,选择截止频率为2.5kHz 的双极点双零点补偿器[27],其传递函数为

其中,Gc0=0.129,零点频率fz=1.72kHz,极点频率fp=14.52kHz,转折频率fL=400Hz,ω=2πf。
选择FBC 中功率补偿器参数时,功率环的带宽应为电压内环带宽的1/10。基于此,选择功率外环补偿器为PI 控制器,其Kp=0.01,Ki=2。
3 仿真结果分析
3.1 不含TAB-PFC 的仿真结果
为验证所提方法的正确性与有效性,在Matlab/Simulink 环境下建立如图11 所示的环形双极直流配电网的模型。其中V1=390V,V2=400V,Rs=0.01Ω,模型中其他参数见表1,系统参数包括电压等级、线路电阻、线路传输功率参考自文献[22,28];TAB-PFC 的参数主要包括滤波电感和滤波电容,滤波电感按纹波电流要求进行设计,滤波电容结合滤波器的剪切频率进行设计[27]。不含TAB-PFC 时正、负极线路潮流分别为24.13kW 与11.47kW,无法达到期望的恒定值10kW。

图11 环形双极直流配电网仿真示意图 Fig.11 Schematic diagram of ring bipolar DC distribution network simulation
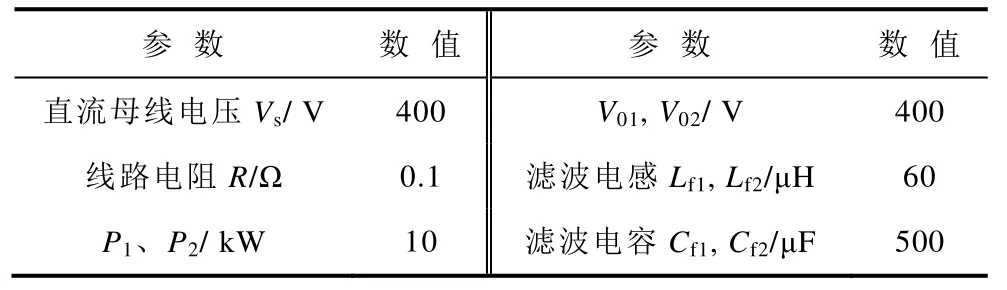
表1 环形双极直流配电网参数 Tab.1 The parameters of ring bipolar DC distribution network
3.2 含TAB-PFC 的仿真结果
TAB 的解耦控制详见文献[29],TAB 采用恒电压控制以使输出电压Vdc恒定。FBC 采用恒功率控制以使线路潮流恒定,其控制策略如图12 所示,其 中iL、vL、Pt分别为传输线路的电流、电压和潮流。分别为Pt和vL的给定值,Gcp(s)和Gcv(s)分别为功率外环和电压内环补偿器。

图12 TAB-PFC 解耦控制框图 Fig.12 TAB-PFC decoupling control block diagram
3.2.1 受端电压不平衡
图13 所示为受端电压不平衡时的仿真结果。其中P、I为线路潮流和线路电流,下标p、n 代表正负极。在0.06s 时,V1从390V 变化至420V,由图13a,Pp与Pn不受V1变化影响,稳定维持在期望值10kW。由图13b,受端电压突变前后线路电流变化较小。对比解耦前后的线路潮流和线路电流,可以观察到在未进行网络解耦前,线路潮流以及线路电流的纹波较大,线路潮流纹波为700W,在经过解耦后,纹波减小,增强了系统的动态性能。
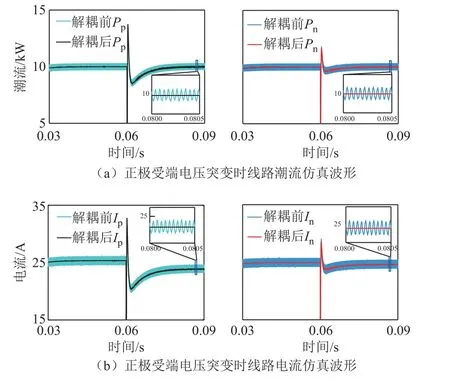
图13 受端电压不平衡仿真结果 Fig.13 Simulations under unbalanced voltage of the receiving end
图14 所示为有无TAB-PFC 时环形双极直流微网线路损耗对比,在0.06s 时,某一极电压发生跳变。由图14 可知TAB-PFC 在控制潮流恒定的同时还能减小线路损耗,与1.3.1 节分析一致。

图14 有、无TAB-PFC 线路损耗对比 Fig.14 Line loss contrast with/without TAB-PFC
3.2.2 新能源出力不平衡
图15 为受端电压平衡(V1=V2=400V),正负极新能源出力不平衡时的仿真结果,各符号代表含义与受端电压不平衡时仿真结果一致。0~0.09s 为稳态建立过程,正、负极新能源出力和受端电压处于额定平衡状态。0.10~0.33s 正极新能源出力模拟24h 内光伏输出,光伏出力变化曲线与1.3.2 节一致,负极光伏出力保持额定值不变。图15a、图15b 所示分别为线路潮流与线路电流波形,可见在TAB-PFC 恒功率控制下,二者均保持恒定。图15c 所示为TABPFC 输出的电压,其随光伏出力的变化而灵活调节。由于负极光伏出力保持恒定,该极TAB-PFC 功率及输出电压变化幅度较正极小。在解耦控制策略下,各波形的纹波均减小,系统的动态性能提高。

图15 光伏出力不平衡仿真结果 Fig.15 Simulations under unbalanced photovoltaic output
4 实验结果分析
为验证本文所提不平衡潮流抑制策略的有效性,搭建了如图16 所示的含TAB-PFC 的双极直流配电网的实验平台,实验平台参数见表2,TAB-PFC采用STM32H750 控制。环形双极直流配电网中,本地负载主要可分为恒阻抗负载(Constant Resistive Load,CRL)和恒功率负载(Constant Power Load,CPL),闭环控制的变换器输出功率恒定,故可视为恒功率负载[30]。本实验中,以输出电阻为20Ω、输出电压控制为恒定10V 的Buck 变换器作为恒功率本地负载进行实验验证。

图16 实验平台 Fig.16 Experimental platform
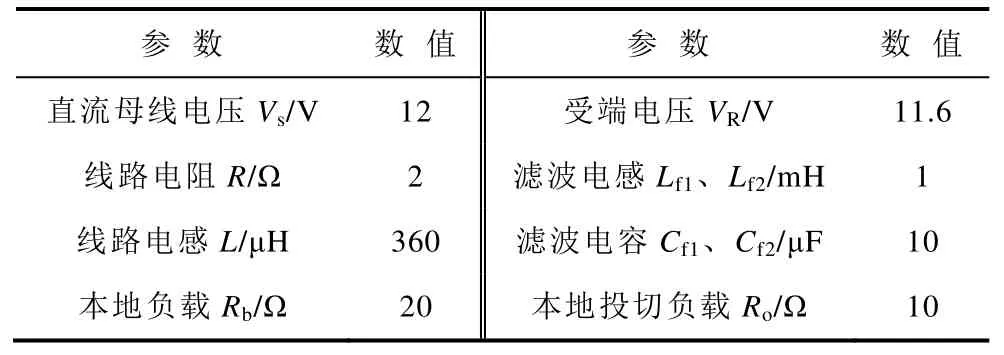
表2 实验平台参数 Tab2 The parameter of experimental platform
4.1 有无TAB-PFC 的实验结果
在正极投切10Ω 的恒阻抗本地负载的实验结果如图17 所示。对比左右图可知,添加TAB-PFC 之后正负极电压、电流均在较短时间内重归恒定值,从而线路潮流也保持为恒定值15W。图17c 右图中潮流范围波动较大的原因是实验电源容量较小。


图17 恒阻抗本地负载有无TAB-PFC 的实验结果 Fig.17 Experimental results of local CRL with/without TAB-PFC
在正极投切输出电阻为10Ω 的恒功率本地负载的实验结果如图18 所示,此时正、负极受端电压分别为10.48V 和10.90V。可见添加TAB-PFC 之后不平衡潮流被抑制,线路潮流亦重归为给定值15W。

图18 恒功率本地负载有、无TAB-PFC 的实验结果 Fig.18 Experimental results of local CPL with/without TAB-PFC
4.2 有无解耦控制的实验结果
正极投切本地负载时的含TAB-PFC 的实验结果分别如图19 和图20 所示。图19 所示为投切恒阻抗负载,图20 所示为投切恒功率负载。投切恒阻抗负载时正、负极受端电压分别为10.6V、11.6V;投切恒功率负载时正、负极受端电压分别为11.12V、11.96V。对比左右图,在TAB-PFC 抑制不平衡功率的基础上,所提解耦控制策略减小了各波形纹波,实现近似解耦。

图19 恒阻抗本地负载有无解耦控制的实验结果 Fig.19 Experimental results of local CRL with/without decoupling control strategy
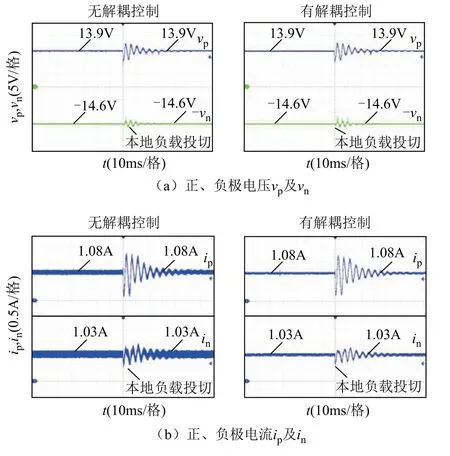

图20 恒功率本地负载有、无解耦控制的实验结果 Fig.20 Experimental results of local CPL with/without decoupling control strategy
5 结论
本文提出了一种基于TAB-PFC 的环形双极直流配电网不平衡潮流抑制策略,可实现灵活调节线路潮流,同时减小线路损耗,提高系统控制的灵活性和运行效率,得到以下结论:
1)TAB-PFC 通过改变串入线路中的电压,可增加环形双极直流配电网控制的自由度。此外,还可抑制由受端电压、新能源出力等不平衡引起的配电网的不平衡潮流。
2)由于存在中线电阻,环形双极直流配电网中TAB-PFC 的控制与输出变量之间存在耦合。通过引入解耦控制矩阵,实现输入和输出之间的近似解耦。
3)所提的解耦控制方法简单易行,为各个控制闭环的独立设计奠定了基础,可有效提高潮流控制的动态性能。
附 录


